绩溪县杉木生长规律分析研究

汪少俊

（绩溪县扬溪林场，安徽 宣城 245331）

绩溪县杉木生长规律分析研究

汪少俊

（绩溪县扬溪林场，安徽 宣城 245331）

本文利用89株杉木样木资料建立了绩溪县杉木的生长方程并进行了分析。结果表明，树高、胸径、材积的生长方程均可采用逻辑斯蒂方程进行模拟；绩溪县杉木的主伐年龄可确定为40年；现行的杉木一元材积表不适宜于绩溪县杉木林分。本研究可以为杉木经营数表的修订或更新提供理论依据。

绩溪县；杉木；生长方程；模型评价；主伐年龄

杉木（Cunninghamia lanceolata）是安徽省重要的用材树种，同时也是最主要的造林树种之一。据统计，安徽省现有杉木林分面积544 892 hm2，主要分布在淮河以南的黄山、宣城、池州、芜湖、铜陵、马鞍山、安庆、六安、合肥9个市，安徽省现有的各种测树数表均为20世纪七、八十年代编制，随着时间的推移，由于树种品系、起源、经营方式以及环境的变化，树木的生长也发生了相应变化，因此研究现在的树木生长规律可以为各种测树数表的修订、更新以及林分可持续经营等提供理论依据。研究树木生长的传统方法是为林木建立各种经验和理论生长方程[1-4]，进而研究其生长规律，但由于树木生长是一个动态、随机的过程，受多因素的影响，使得树木生长随年龄的变化，表现出复杂的非线性，各种模型难以如实描述树木生长状态与年龄的非线性关系，模拟和预测结果难以达到理想的效果，因此也有采用神经网络等高新技术对树木进行模拟，这些技术对于非线性问题建模有很好的拟合性，非常适合于解决林业问题[5-8]。笔者利用近年来积累的杉木样木资料建立了绩溪县杉木生长方程并对其进行了分析研究，以期为安徽省杉木经营数表的修订、更新以及杉木林分的经营管理提供理论依据。

1 研究地概况

绩溪县位于安徽省东南部，地处118°20′～118°55′E，29°57′～30°20′N之间，黄山支脉和天目山支脉结合部，是一个含中山的低山丘陵县，境内山峦起伏，河谷深切，地形地貌复杂，整个地势由东北向西倾斜，海拔多在300～600 m；县境内基岩以花岗岩、石灰岩、闪长岩、砂砾岩为主，地带性土壤为红壤，土壤垂直带谱明显；气候属中亚热带季风性湿润气候区，年平均气温15.9 ℃，年积温（≥10℃）为4 979.4 ℃，年日照时数1 926.4 h左右，无霜期233 d；年平均降雨量1 500 mm，降雨年际年内分配不均，主要分布在4～7月份，降雨量占全年的40%～60%；绩溪县植物种类繁多，共有各类树种540多种，野生植物资源1 000多种，地带性植被为常绿与落叶阔叶混交林带，但由于人为破坏等原因，原始林已不复存在，现存的都是人工林和天然次生林，主要造林树种有杉木、马尾松、湿地松、火炬松、枫香、毛竹等，天然林主要组成树种有苦槠、甜槠、青冈栎、麻栎、枫香等。

2 材料与方法

2.1 资料来源

作者自2009年至2014年5年间，从绩溪县不同地区不同立地条件的人工杉木林分内随机收集了89株杉木样木，样木年龄在9～52年之间，胸径在6～40 cm，树高在4～23 m之间。

2.2 数据采集方法

将样木伐倒，用皮尺量测树高h；并按中央断面区分求积（区分段长度为1 m）的方法在各段中央处以及梢头底直径处利用直径卷尺量测各部位直径以及胸径，在此基础上计算样木材积；样木年龄通过查数伐根年轮数确定。

2.3 数据处理

将样木的胸径、树高、材积及年龄值输入Excel电子表格中，分龄阶计算各龄阶的平均高、平均胸径、平均材积及其标准差，按照3倍标准差将错误或异常数据剔除，经计算本次未剔除。

2.4 选择数学模型

将经处理后剩下的数据，以年龄为横坐标、各调查因子为纵坐标绘制散点图，如图1所示。

根据散点图情况及树木生长规律选择以下方程（1）、（2）、（3）作为树木生长方程的初选模型（除此3方程外，本研究也用多个理论及经验生长方程进行了模拟，但效果均不好，鉴于篇幅，不作赘述）：

其中：y为样木各年龄的树高、胸径及材积值，A为年龄，a0、a1、a2等为模型参数。在DPS数据处理系统[9]下求解初选模型各参数，通过对方程的评价选择一个最佳模型作为模拟杉木生长的最终生长方程。

2.5 数学模型的评价[10]

2.5.1 评价指标

（1）离差平方和SSR：

里查德方程

（2）相关系数R：

（3）总相对误差RS：

（4）相对误差平均值REA：

（5）相对误差绝对值平均值REAA：

（6）残差（SR）图：

以自变量为横轴、残差为纵轴建立直角坐标系，绘制残差分布图。残差计算如下：

（7）数学模型行为分析：

最小与最大径阶模型估计值与实测值的差异及其变化趋势。

2.5.2 数学模型有效性

当RS小于3%且大于-3%时，数学模型有效，否则应舍弃，或重新构建模型，直至满足RS小于3%且大于-3%的要求。

2.5.3 数学模型确定原则：

——离差平方和小；

——相关系数大；

——总相对误差小；

——相对误差平均值小；

——相对误差绝对值平均值小；

——残差图以横轴为中心分布均匀；

——在数学模型行为分析中，估计值与实际值的差异不因因变量变小而增大，也不因因变量增大而增大。

当上述各指标不一致时，应优先考虑相对误差绝对值平均值REAA、总相对误差RS、残差图指标并进行综合评价后确定。

根据以上指标体系，从初选模型中选择最优方程作为最终模型。

3 结果与分析

3.1 模型参数的求解及最佳生长方程的确定

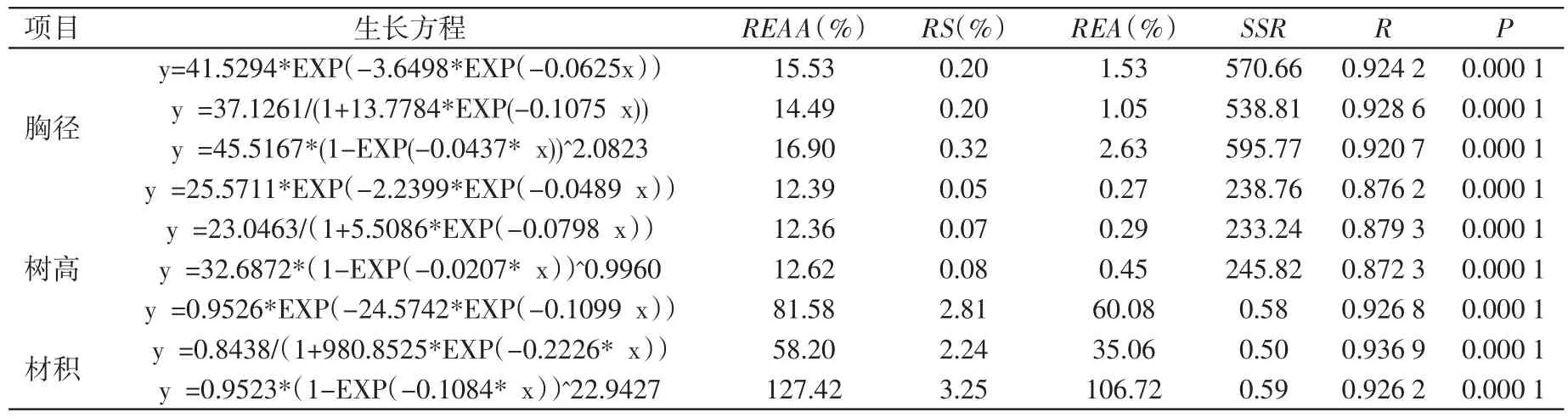
表1 模型回归参数及评价指标表

利用DPS数据处理系统求解以上各模型参数，其结果如表1、图2所示。由表1可以看出，模拟杉木胸径、树高及材积生长的各方程的相关系数在0.87以上，且其显著水平P=0.000 1＜0.01，为极显著水平，说明以上各模型关系均极显著；3个方程的RS值均小于3%且大于-3%，因此所有模型均有效。胸径、材积的各生长方程中，逻辑斯蒂方程的各评价指标都是最好的；树高各方程中逻辑斯蒂方程的REAA值、SSR值最小，相关系数R最大，RS、REA值中等且与最好的相差无几；各模型残差图均以横轴为中心均匀分布且估计值与实际值的差异不因因变量变小而增大，也不因因变量增大而增大（见图2）。因此综合考虑选择逻辑斯蒂生长方程作为模拟绩溪县杉木胸径、树高及材积生长的最佳生长模型，其方程见表1所示。

3.2 杉木生长规律

利用上述最佳生长方程分别计算各年龄的树高、胸径和材积总生长量，并按公式计算其连年和平均生长量[1]，见表2。

表2 杉木生长过程表

由表2可以看出，在杉木整个生长过程中，树高、胸径和材积均经历了一个缓慢—旺盛—缓慢的生长过程，其连年生长量在40年时仍分别可达到0.284 m、0.549 cm、0.021 22 m3，年平均生长量分别达到0.470 m、0.782 cm、0.018 61 m3，生长速度快；连年生长量树高先达到最大值（22年），然后是胸径（25年），最后是材积（31年），这表明杉木早期树高生长较快，之后胸径仍然维持一段时间的高速生长，这有利于材积的积蓄；材积是树高和胸径累积的结果，因此在树高和胸径生长均达到高峰后还能保持一定时间的高速增长，材积连年生长量在31年生时达到最大值，其值为0.046 79 m3，与材积平均生长量曲线相交于40年，即材积平均生长量在40年时达到最大值，其值为0.018 61 m3，此时达到数量成熟；40年后杉木的胸径、树高和材积的连年生长量下降较快，此时应当进行采伐。根据以上分析结果，可以大致把杉木整个生长发育过程划分为三个阶段：幼龄林期（0～20年）、中龄林期（21～35）、近熟林期（36～40年），41年以后为成熟林期。

3.3 杉木主伐年龄的确定

在林业上一般以材积年平均生长量最大的那一年作为树木的数量成熟龄，它是确定合理采伐年龄的重要依据。由表2可以看出，绩溪县杉木的材积年平均生长量最大值出现在第40年，且在之后的几年中连年生长量下降较快。因此，综合考虑，可以40年作为杉木用材林的主伐年龄，据此合理安排杉木用材林林分的各项经营措施。

3.4 现阶段绩溪县杉木生长与1985年以前生长对比

根据胸径最佳生长方程倒推出相应径阶中值的年龄，将此年龄值代入材积最佳生长方程求算出材积，即可知对应胸径的材积值；然后在1985年版的《林业调查设计常用手册》[11]上查出相应径阶中值的杉木一元材积表上的材积值；将这2组材积值进行方差分析，结果如表3。由表3可以看出，区组间（同一胸径）及处理间（2组材积）的显著水平P＜0.05，说明现阶段绩溪县杉木的单株材积与1985年前相比，无论是同一胸径的材积间还是整体的材积均有显著差异，同时现阶段这组数据的材积平均值为0.289 9 m3，而1985年前为0.340 9 m3，这表明随着时间的推移，当地的气候、立地条件以及经营的变化，对树木的生长产生了较大影响，导致了其材积生长降低。

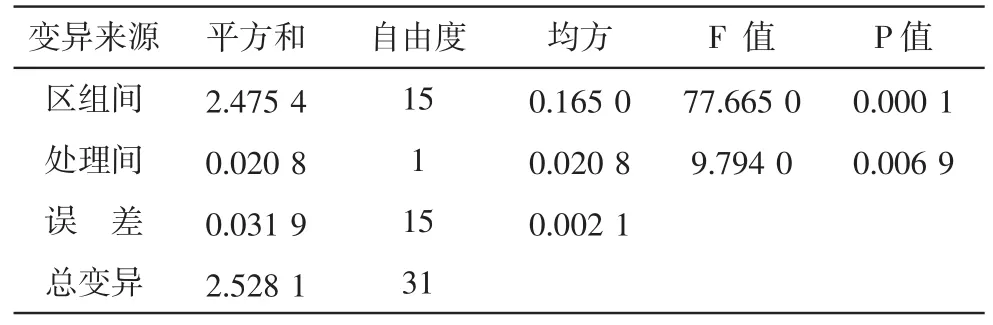
表3 方差分析表

4 结论与讨论

（1）可以采用逻辑斯蒂生长方程模拟绩溪县杉木生长，其方程分别为：=23.0463/（1+5.5086*EXP（-0.0798 x））（树高），y=37.1261/（1+13.7784*EXP（-0.1075 x））（胸径），y=0.8438/（1+980.8525*EXP（-0.2226* x））（材积），其相关性高，方程适用。

（2）本研究结果表明，绩溪县现阶段杉木生长指标不如以前，这与现在很多的杉木林分是二代林甚至是三代林有一定关系，但更与杉木林分的疏于管理有很大的关系，因此在今后的营林过程中，一定要重视杉木林分的合理抚育间伐及杉木多代林的改造。

（3）安徽省杉木用材林现在执行的主伐年龄为26年，但根据本次调查结果，并结合国家大径材短缺且中小径材市场乏力的现状，建议可以将绩溪县杉木人工用材林主伐年龄调整为40年，据此合理安排杉木用材林林分的各项经营措施。杉木早期树高生长较快，因此早期密植，可以塑造良好的干形，到一定时期以后再进行合理间伐，以促进胸径及材积的生长并提高出材率。

（4）目前绩溪县杉木的材积生长与现在仍在使用的1985年版的《林业调查设计常用手册》上的材积量有明显的差异，有必要对现有数表进行更新或修订。

（5）本文仅对绩溪县杉木生长规律进行了分析，建议在更大范围内采集数据进行分析评价，为修订或更新安徽省现有杉木数表提供理论依据。

[1]北京林业大学.测树学[M].北京：中国林业出版社，1986.

[2]张忠远，贺民.杉木人工林的生长及生长模型[J].安徽农学院学报，1992，19（3）：202-208.

[3]黄家荣，杨世逸，温佐吾.杉木人工林的单木胸径生长模型研究[J].贵州农学院学报，1994，13（1）：12-16.

[4]吴泽民，李宏开，束庆龙.现代林业研究方法[M].北京：中国林业出版社，1999.

[5]姚东，李际平.BP模型在单木树高与胸径生长模拟中的应用[J].中南林学院学报，1996，16（3）：34-36.

[6]刘永霞，冯仲科，杜鹏志.Elman动态递归神经网络在树木生长预测中的应用[J]. 北京林业大学学报，2007，29（6）：99-103.

[7]马友平，张志华，艾训儒，等.日本落叶松生长的经验方程与灰色GM（1，1）模型研究[J]. 数学的实践与认识，2008，38（23）：86-90.

[8]雷相东，常敏，陆元昌，等.虚拟树木生长建模及可视化研究综述[J].林业科学，2006，42（11）：123-129.

[9]唐启义，冯明光.实用统计分析及其DPS数据处理系统[M].科学出版社，2002.

[10]国家林业局《一元立木材积表编制技术规程》

[11]安徽省林业勘察设计院.林业调查设计常用手册[M]. 1985.

Analysis on the Growth Rhythm of Cunninghamia lanceolata in Jixi County

WANG Shaojun
（State-owned Yangxi Forest Farm of Jixi County,Xuancheng 245331,Anhui,China)

In this paper the data of 89 sample trees of Cunninghamia lanceolata were used to establish the growth equations of Cunninghamia lanceolata in Jixi County and the data were analyzed.The results showed that the growth equations of the tree height,DBH and volume could be simulated with Logistic equations.The final felling age of Cunninghamia lanceolata plantations in Jixi County could be set at the age of 40.The current one-way volume table of Cunninghamia lanceolata isn’t suitable for the stands in Jixi County.The study could provide theoretical basis for revising and updating the management numerical tables of Cunninghamia lanceolata.

Jixi County;Cunninghamia lanceolata;Growth equations;Model evaluation;Final felling age

S791.27

A

2095-0152（2015）03-0012-05

2015-04-09

2015-05-15

汪少俊（1970- ），男，林业工程师，主要从事林业技术管理工作。E-mail:247397070@qq.com

杨婷婷）