非专业弱关联影像的地理配准及其精度评估

引文格式：LIU Yingzhen, JIA Fenli, WAN Gang, et al.Geo-registration of Unprofessional and Weakly-related Image and Precision Evaluation[J]. Acta Geodaetica et Cartographica Sinica,2015,44(9):1014-1021.(刘颖真，贾奋励，万刚，等.非专业弱关联影像的地理配准及其精度评估[J].测绘学报，2015,44(9)：1014-1021.) DOI:10.11947/j.AGCS.2015.20140394

非专业弱关联影像的地理配准及其精度评估

刘颖真1,2,3，贾奋励4，万刚4，诸云强2，霍超5

1. 总参谋部测绘信息中心, 北京 100088; 2. 中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室，北京 100101; 3. 中国科学院大学，北京 100049; 4. 信息工程大学地理空间信息学院，河南 郑州 450052; 5. 西安测绘总站，陕西 西安 710054

Geo-registration of Unprofessional and Weakly-related Image and Precision Evaluation

LIU Yingzhen1, 2, 3,JIA Fenli4,WAN Gang4,ZHU Yunqiang2,HUO Chao5

1. General Staff Information Center of Surveying and Mapping, Beijing 100088, China； 2. State Key Laboratory of Resources and Environmental Information System, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China; 3. University of Chinese Academy of Sciences, Beijing 100049, China; 4. Geospatial Information Institute, Information Engineering University, Zhengzhou 450052, China; 5. Technical Division of Surveying and Mapping, Xi’an 710054, China

Abstract：The 3D geo-spatial model built by unprofessional and weakly-related image is a significant source of geo-spatial information. The unprofessional and weakly-related image cannot be useful geo-spatial information until be geo-registered with accurate geo-spatial orientation and location. In this paper, we present an automatic geo-registration using the coordination acquired by real-time GPS module. We calculate 2D and 3D spatial transformation parameters based on the spatial similarity between the image location in the geo-spatial coordination system and in the 3D reconstruction coordination system. Because of the poor precision of GPS information and especially the unstability of elevation measurement, we use RANSAC algorithm to get rid of outliers. In the experiment, we compare the geo-registered image positions to their differential GPS coordinates. The errors of translation, rotation and scaling are evaluated quantitively and the causes of bad result are analyzed. The experiment demonstrates that this geo-registration method can get a precise result with enough images.

Key words： 2D geo-registration; 3D geo-registration; GPS information of image; parameter solution of geo-registration; quantitive evaluation of geo-registration precision

Foundation support： The National Natural Science Foundation of China (Nos.40971239;41371381;41101437; 41371383; 41201390)；The Specific Foundation of Fundamental Scientific Research of China (No.2013FY110900)；The National Foundation of Major Scientific Equipment Development of China (No.2012YQ06002704)；The Science and Technology Plan Projects of Yunnan Province (No.2012CA021)

摘要：由非专业弱关联影像自动化构建的三维地理空间模型是地理空间信息的重要来源。非专业弱关联影像在三维重建后必须经过地理配准，具有了绝对地理空间坐标系的位置信息及其准确的空间精度信息后，才有可能成为有效的地理空间信息。本文提出了一种以相机GPS模块获取的地理空间坐标为依据的理配准方法，依据影像的地理空间坐标和其三维重建后得到图像空间坐标的空间相似性，考虑GPS实时测量坐标精度较差和高程测量值不稳定的特点，采用RANSAC方法求解二维和三维两种空间变换参数及地理配准结果。利用差分GPS测量的影像位置数据对地理配准的精度进行了分析，给出了位移、旋转和缩放等误差的定量评估结果，分析了产生错误结果的原因。这种地理配准方法对数据采集设备要求低，过程无须人工参与。试验证明，在参与地理配准运算的照片数量较多时，配准结果正确、空间精度较高。

关键词：二维地理配准;三维地理配准;影像GPS信息;地理配准参数求解;地理配准精度定量评估

中图分类号：P208

基金项目：国家自然科学基金(40971239；41371381；41101437；41371383；41201390)；科技基础性工作专项(2013FY110900)；国家重大科学仪器设备开发专项(2012YQ06002704)；云南省科技计划(2012CA021)

收稿日期：2014-07-23

作者简介：第一 刘颖真(1981—)，女，博士，研究方向为三维地理信息构建与人机交互。

1引言

非专业弱关联影像(unprofessional and weakly-correlated image)是指由非专业人员采用普通方式拍摄获取的、相互间存在弱空间关联关系的照片或序列影像[1]。随着消费级数码相机和带有高清拍摄功能手机的日渐普及，普通民众已经可以随时随地采集感兴趣对象的照片。针对同一对象重叠度较高的拍摄即可获得非专业弱关联影像，这让非专业弱关联影像的采集变得极为方便、快捷。同时，得益于计算机视觉的发展，利用非专业弱关联影像重建三维场景的技术已经日趋成熟，具有对处理设备要求不高、处理方法自动化程度高、处理过程耗时短等特点。将非专业弱关联影像作为地理空间信息获取的来源，具有重要的研究意义和广阔的应用前景。

非专业弱关联影像通过计算机视觉技术恢复的三维影像和点云是在一个完全由图像信息恢复出来的相对三维空间(下文简称为像空间)坐标系中，既没有绝对的地理位置，也没有绝对的空间度量标准，不能成为有效的地理空间信息来源。因此必须借助额外的地理空间位置信息，通过地理配准使其具备地理空间坐标系的绝对坐标。地理配准后数据还需要经过空间精度评估，才能确定其适用领域。地理配准的精度主要由配准使用的地理空间位置信息和配准方法决定，而对这个精度的评估，需要有更高精度的地理空间数据作支持。

目前关于三维重建照片和点云的地理配准的研究很多，原理总结如图1所示。地理配准采用的基准地理信息包括用户指定的照片位置信息[2-3]、地图[4]、具有位置信息且经过训练的正射高清遥感影像[2]、楼层内部结构图[2]、LiDAR点云[5-7]、有位置信息的三维重建点云[8]、DSM模型和相机GPS模块获取的位置信息[9-12]、飞行器的GPS数据[7, 13]、Google全景图[14]、Google街景地图和Google地球三维模型[3]，等。地理配准的方式主要分为全自动计算[3, 9-12, 14-15]和需要人工参与的半自动计算两种方式，其中人工参与的工作包括指定位置[2]、比例尺[2]、基准地理信息和待地理配准数据的对应点[5-6]等。地理配准的方法主要分为两类，一类是基于图像特征相似度的，如提取卫星影像、地图、楼层结构图等二维图像中墙面的图像特征作为配准基准，利用投影处理后的点云及其与相机之间的可视化关系推算出墙面的空间位置，然后进行配准[2]；另一类是基于空间位置一致性的，如把三维点云与Google地球三维模型[3]SM模型[9]配准，利用人工指定图像与LiDAR点云的对应特征点后用最小二乘的方法计算配准的几何变换参数[5-7]，利用已有照片集中照片的地理位置，配准新加入重建计算的照片等[8, 11]。

图1　三维重建照片和点云的地理配准方法原理 [1] Fig.1　Geo-registration methodology of 3D reconstruction [1]

对于地理配准结果的精度，只有一部分研究给出了定量的评估结果，且其中一部分没有给出定量结果的计算方法。文献[3]给出了多组数据的拍摄位置平均误差，范围在1.86～595.20m，其中拍摄位置的真值一部分是靠手工配准三维点云到Google地图中的卫星影像，一部分来自照片所带的精确差分GPS坐标。文献[6]给出了拍摄位置的平均角度误差约为0.1°，仅用LiDAR点云和照片叠加的方法说明地理配准精度较高，但是没有给出精度评估的方法。文献[10]以10个固定拍摄点的差分GPS坐标为真值定量评估了地理配准结果，这10个拍摄点在二维地平面上的平均偏移为0.31±0.04m。文献[13]给出了标示点的地理注册坐标和测量坐标之间的3个方向的距离误差，其中一个方向的最大误差达到15m。文献[7]仅给出了地理配准后的影像和Google地图相差2.5m的结果。

非专业弱关联影像的优势在于数据获取方法简单快捷、处理过程无须人工参与，因此针对该类影像的地理配准方法应尽量简化对采集设备和基准地理数据的要求。本文研究的地理配准算法仅需要相机配备GPS模块(当前的很多智能手机都自带GPS模块)，以其自动实时获取的地理坐标为基准地理信息，配准的对象为非专业弱关联影像重建得到的影像拍摄位置和三维点云位置，配准过程为全自动处理。地理配准结果的精度评估以部分相机的差分GPS坐标为真值，评估指标包括了每组重建结果中拍摄位置在二维地平面和三维空间中的位移、旋转角度和缩放比例等。

2利用影像GPS信息的地理配准方法

相机内置或加配的GPS定位模块虽然操作简单，易于快速地实现实时定位，但是由于定位过程中受到卫星星历误差、钟差及信号传播误差等诸多因素的影响定位精度不高，一般为10～50m[16]，高程测量值较水平坐标的稳定性更差。因此，本文设计了两种地理配准参数求解方法，一种是使用GPS测量的水平经纬度坐标和高程坐标的三维地理配准方法，另一种是仅使用水平经纬度坐标的二维地理配准方法。考虑到GPS测量的精度较差，采用随机抽样一致性(random sample consensus，RANSAC)算法选取部分影像的GPS坐标求解最优配准参数，结合第3部分试验中精度评估结果，经过反复试验后确定了算法中各种参数和外点的判断标准。

2.1　三维地理配准参数求解方法

如图2所示，基于三维摄影变换关系的地理配准方法运算过程相对简单，主要原理是根据每张影像重建得到像空间三维坐标pI和拍摄时由GPS模块获取的地理空间三维坐标pG，运用机器视觉中含有比例因子的绝对定位方法[17]，求解像空间和地理空间这两个三维空间之间的坐标变换关系，得到每张影像的地理配准坐标pA。其中地理空间的三维坐标pG是由影像的GPS坐标(WGS-84坐标系)转换到大地直角坐标系得到的。

图2　基于三维摄影变换关系的地理配准方法流程图 Fig.2　Flow diagram of geo-registration using 3D space transformation

设同一幅影像的像空间三维点为pI=[xIyIzI]T、地理配准后得到的地理空间大地直角坐标系点为pA=[xAyAzA]T，从像空间到地理空间的坐标系变换公式为

pA=sRpI+p0

(1)

式中，s是比例因子，R是旋转矩阵，p0是平移矢量。待求解的地理配准参数共有7个：3个旋转参数，3个平移参数，1个比例因子。已知的是点群pI和点群pG。

(2)

(3)

将每个点群变换为有关矩中心的一个矢量簇rI,i和rG,i

(4)

(5)

计算矢量簇平均长度，即可确定比例因子s

(6)

计算两个点群中的射线坐标标量积之和，得到矩阵M

(7)

为求解旋转矩阵R，并保证R是规范化正交矩阵，设矩阵Q为

Q=MTM

(8)

设矩阵S为

S=Q1/2

(9)

计算Q的特征值λ1、λ2、λ3和特征矢量v1、v2、v3，将矩阵的分解表示为

(10)

可求解矩阵S的逆矩阵

(11)

则旋转矩阵R为

R=MS-1

(12)

根据求解得到的s、R，即可根据公式

(13)

求解得到平移矢量p0。

根据求解得到的s、R和p0，即可根据式(1)求解得到像空间内每个拍摄位置的地理配准坐标pA和点云中每个点对应的地理空间三维坐标。

这种基于三维摄影关系的地理配准方法原理简单、适用范围广，既可以用于非专业弱关联影像，又适用于有GPS航迹信息的无人机影像。但需要注意的是，普通GPS接收单元采集的高程信息精度较差，造成配准结果精度低于二维地理配准方法(参见后面的试验结果)。

2.2　二维地理配准参数求解方法

如图3所示，基于二维投影变换关系的地理配准方法与基于三维的地理配准方法流程相同，不同点是在两种空间下的影像拍摄位置坐标都是经过了投影处理后得到的二维坐标，最终的地理配准结果也是二维平面上的地理空间坐标而没有高程信息。二维地理配准运算的重点是如何对像空间中的影像拍摄位置进行降维度投影处理。本文采用高斯投影变换将地理空间中的影像GPS位置转换为二维投影坐标；采用Szeliski的方法[18]求解所有影像的向上矢量，然后以该矢量方向为地平面的法向量，即可计算影像的二维投影位置。

Szeliski的方法是根据普通用户拍摄影像通常为水平手持拍摄的特点，假设影像的横边和地面平行，推算出地平面的法向量，把影像的拍摄位置和点云等所有相对坐标系下的三维点p简化为仍处于相对坐标系下的二维地面投影点p′。

在算法上，就是求解一个3×3的旋转矩阵Rg，使得

p′=Rgp

(14)

式中，p′所在的坐标系满足y轴垂直于地面。设

(15)

分步求解每一行rg0、rg1和rg2。

首先求解rg1。rg1是每幅影像的旋转矩阵Rk中x向量rk0的矩量矩阵的最小特征向量，即

(16)

式中，rk0=[100]Rk，即旋转矩阵的第1行。

接下来，求解rg0和rg2

(17)

rg2=rg0×rg1

(18)

式中，rk2=[001]Rk，即旋转矩阵的第3行。

假设像空间中影像点p=[xyz]，投影的地面点p′=[x′y′]，则

(19)

接下来二维空间坐标系的地理配准参数求解方法与2.1节中的三维地理配准参数求解方法相同，不再赘述。

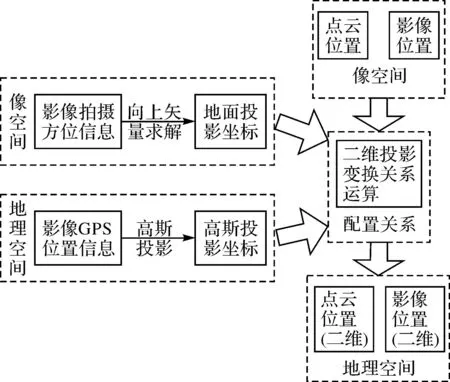
图3　基于二维投影变换关系的地理配准方法流程图 Fig.3　Flow diagram of geo-registration using 2D space transformation

2.3　用 RANSAC的方法求解最优地理配准参数

由于GPS实时测量的坐标误稳定性差，存在一些误差较大的错误点。如果使用所有影像拍摄位置的GPS坐标计算地理配准参数，会受到这些误差较大点的影响，得到并非最优的配准方案，因此需要一种容错能力强的算法。本文设计了一种RANSAC算法[19]，经过反复试验确定了算法中的各种参数和外点判断标准。

2.3.1　算法步骤

(1) 设置置信概率P、数据错误率ε、最小抽样数m，根据

1-(1-(1-ε)m)M=P

(20)

计算需要的抽样数量M。

(2) 随机抽取m个影像拍摄点，按照2.1节或者2.2节的方法用其GPS测量坐标pG和像空间坐标pI计算对应的一组地理配准参数。

(3) 根据步骤(2)中得到的地理配准参数，用所有影像拍摄点的像空间坐标pI计算对应的配准地理坐标pA，计算pG到pA的距离DisGA，根据DisGA与阈值的关系判断每一个点是否为内点，获得这组配准参数的内点数量。

(4) 重复步骤(2)和步骤(3)，直到完成M次抽样的处理。

(5) 根据内点数量选择最优的地理配准参数。

(6) 找出最优的地理配准参数对应的所有内点，用这些内点计算最终的配准参数。

2.3.2　算法参数设置

在这个RANSAC算法中，需要设置的参数包括置信概率P、数据错误率ε、最小抽样数m和判断外点需要的pG到pA的三维距离DisGA和二维距离DisGA2d的阈值。本文统计分析了精度评估试验(详见3.3节)中获取的相机位置差分GPS坐标pD到pG之间的二维地面投影距离DisGD2d、高差HeitGD以及三维距离DisGD，以此确定算法中的上述参数。

图4按照精度评估试验中测量的4个建筑物分布绘制了DisGD2d、HeitGD和DisGD的箱型图。由图4可见，pG和pD之间二维距离DisGD2d(填充色为白色)的内距(inter-quartile range，IQR)为10～15m。因此，将二维地理配准中DisGD2d的阈值设置为15m，置信概率P=0.95，数据错误率ε=0.65。三维距离DisGD(填充色为深灰色)的高程分量HeitGD(填充色为浅灰色)的误差较DisGD2d普遍偏大，是造成DisGD稳定性差的主要原因。尽管如此，可以看出，DisGD的第二分位数都在25m以内，因此三维地理配准中设置DisGD的阈值为25m，P=0.95，ε节=0.5，二维和三维地理配准中的最小抽样数m分别设为7和9。

图4　实时GPS测量坐标p G和差分GPS测量坐标p D之间二维距离、高差和三维距离的箱型统计图 Fig.4　Box chart of the 2D distance, height difference and 3D distance between GPS coordinate p G and differential GPS coordinate p D

3利用差分GPS信息的地理配准试验

3.1　试验数据

为了验证地理配准算法的正确性并评估配准结果的精度，选取位于河南省郑州市的4个建筑物，由6个人手持多台配备GPS定位模块的数码相机和自身带有拍摄功能和GPS定位功能的智能手机，分两次拍摄了920余张带有实时GPS测量坐标的建筑物立面照片。在第2次拍摄中，用差分GPS设备测量了305张照片拍摄点的精确坐标。选取的拍摄对象既有轮廓相对简单、纹理相对重复的建筑物，也有轮廓和纹理都较为复杂的建筑物。图5为建筑物1三维重建得到的点云和参与配准试验的原始照片。

图5　建筑物1的三维重建点云和参与配准运算的照片 Fig.5　3D reconstruction point cloud and original photos for geo-registrationof No.1 building

3.2　试验设备

拍摄设备：尼康D5100相机，焦距18～105mm，分辨率3696像素×2448像素；尼康D90相机，焦距18～105mm，分辨率4288像素×2848像素；苹果iPhone 4S手机自带相机，焦距4mm，分辨率3264像素×2488像素；苹果iPhone 3GS手机自带相机，焦距4mm，分辨率1536像素×2048像素。

GPS接收器：尼康GP-1(数码相机配备)，水平精度为10m RMS[20]；手机使用自带GPS模块。

差分GPS设备：南方S82T，水平精度1cm+1×10-6D，垂直精度2cm+1×10-6D[21]。

3.3　地理配准试验结果及分析

对各个建筑物按照每个单一时段和多时段集合的方式分别进行了三维重建和地理配准运算。分析结果表明，在参与地理配准运算的照片数量较多时，地理配准算法结果正确，配准精度令人满意。地理配准结果的误差或错误主要出现在平移、旋转、缩放等方面。

3.3.1　结果误差的定量评估

为了定量评估地理配准中照片拍摄位置的平移、旋转和缩放的精度，本文把每组照片的配准坐标和其差分GPS坐标进行了各种统计和解算。将拍摄点的地理配准坐标pA与差分GPS坐标pD的距离DisDA进行统计分析，得到平移误差的均值和标准差；采用2.2节中的二维地理配准参数求解方法，计算了pA与pD之间的空间关系变换参数，即比例因子和旋转矩阵，由此计算旋转角度误差和缩放比例误差。为便于对二维和三维两种地理配准方法的误差作比较，三维地理配准结果的旋转角度误差和缩放比例误差是用pA与pD的二维高斯投影坐标计算的，同时也计算了平移误差的二维数值。表1详细给出了每个地理配准结果的误差计算值(黑体部分为错误结果)。由表1可以看出，在照片较多时，地理配准结果的误差都较小，表明配准结果正确。

表1　地理配准结果详细误差表

在正确的地理配准结果中，普遍存在平移误差(图6为典型示例)，二维地理配准结果的平移误差均值为3.31～7.68m、标准差为0.24～1.65m，三维地理配准结果的平移误差均值为5.92～9.58m、标准差为1.33～2.62m，其地面投影的二维平移误差均值为2.72～7.48m，标准差为0.90～2.78m。二维地理配准的平移误差均值略大于三维配准，但是标准差较小。旋转误差普遍较小，角度都在±5.6°以内，二维地理配准的旋转误差和三维配准相差不大。缩放误差也普遍较小，缩放比例为0.99～1.13之间，二维地理配准的缩放误差小于三维配准。在三维地理配准结果中，高程误差的标准差普遍大于地面投影的二维平移误差标准差，是造成三维平移误差大的主要因素。二维和三维两种地理配准方法相较而言，二维方法稳定性更高，平移误差的标准差和缩放误差较小。但是由于照片的GPS坐标稳定性差，可能出现照片增多时GPS坐标误差更大的情况(如表1中的建筑物3)，因此在照片达到一定数量之后，地理配准的精度并没有随着照片数量的增加而明显改善，甚至会在一些指标上出现下降。对于本文的试验结果，在照片多于80张时，得到的结果都是正确结果。

文献[3]中给出了7个建筑物利用照片的GPS信息(一部分是相机内置的GPS模块实时获取，一部分是人工指定的，人工指定的GPS信息误差较大)和照片中线段的灭点信息计算的二维地理配准结果误差，照片位置的平移误差均值分别为3.41m、9.42m、13.69m、14.03m、20.05m、34.55m、245.49m和595.20m。与本文试验结果中二维地理配准结果的平移误差均值为3.31～21.52m(包括错误的配准结果)相比，本文的方法在精度上表现较好。

图6　建筑物4多时段照片的地理配准结果(145张照片参与地理配准运算，图中仅显示有差分GPS坐标的照片位置) Fig.6　Geo-registration result of No.4 building using multi-period photos (145 photos involved in calculation, only the ones with differential GPS coordinates are displayed)

3.3.2　错误地理配准结果的分析

如表1中黑体部分所示，有3个建筑物在参与地理配准运算的照片较少(都少于60张)时，出现了误差较大的错误结果。错误的表现有旋转角度过大(图7(a)为典型示例)、整体缩小或放大的比例过大(图8(a)为典型示例)等现象(详细的错误数值参见表1中加下划线的数值)。比较pG和pD的空间分布发现，各个错误结果中从pD到pG的矢量vDG存在方向上的聚集性(见图7(b)和图8(b))，即GPS模块实时测量的坐标与真值相比，普遍偏向一个方向。那么运算出的地理配准结果pA的分布也会朝向这个方向。这表明，当参与地理配准运算的照片数量较少时，如果实时GPS的测量误差在空间分布上存在方向的非均匀性，会引起地理配准结果出现方向相同的错误。而照片数量越多，测量误差出现这种方向上非均匀性情况的概率越低。

4结论

本文提出了一种利用相机配备的GPS模块在拍摄时实时测量的地理空间坐标对非专业弱关联影像的三维重建结果进行地理配准的全自动化方法。考虑到GPS实时测量坐标精度较差和高程测量不稳定的特点，采用RANSAC方法求解二维和三维两种空间变换参数及配准结果。利用差分GPS测量的影像位置数据对地理配准结果的精度进行了多指标的定量评估，对错误结果进行了分析。该地理配准方法适用于手持拍摄的室外地物照片，仅要求照片数量足够多、相机配备GPS模块即可。该方法的特点是对数据采集设备要求低，过程无须人工参与，且对照片的初始定位数据测量精度要求不高。地理配准试验的精度评估结果表明，该方法在参与运算的照片数量在80张以上时，二维和三维两种地理配准方法的结果均正确，空间精度较高。

图7　利用建筑物1某单一时段照片得到的错误的地理配准结果(30个拍摄点参与地理配准运算) Fig.7　Wrong geo-registration result of No.1 building using single-period photos (30 photos involved in calculation)

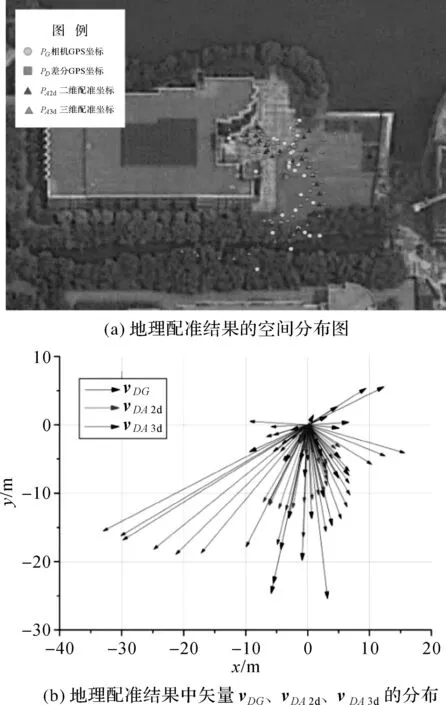
图8　利用建筑物2某一时段照片得到的错误的地理配准结果(28个拍摄点参与地理配准运算) Fig.8　Wrong geo-registration result of No.2 building using single-period photos (28 photos involved in calculation)

参考文献：

[1]LIU Yingzhen, JIA Fenli, WAN Gang, et al. Construction and Application of 3D GIS Based on Unprofessionaland Weakly-Correlated Image[J]. Journal of Geomatics Science and Technology, 2014, 31(1): 73-78. (刘颖真, 贾奋励, 万刚, 等. 非专业弱关联影像构建三维GIS研究[J]. 测绘科学技术学报, 2014, 31(1): 73-78.)

[2]KAMINSKY R S, SNAVELY N, SEITZ S M, et al. Alignment of 3D Point Clouds to Overhead Images[C]∥IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops. Miami: IEEE, 2009:63-70.

[3]WANG Chunpo, WILSON K, SNAVELY N. Accurate Georegistration of Point Clouds Using Geographic Data[C]∥2013 International Conference on 3D Vision. Seattle: IEEE, 2013:33-40.

[4]ROBERTSON D P, CIPOLLA R. Building Architectural Models from Many Views Using Map Constraints[C]∥HEYDEN A,SPARR G,NIELSEN M, et al.The European Conference on Computer Vision 2002. Copenhagen: Springer, 2002: 155-169.

[5]CHO P. 3D Organization of 2D Urban Imagery[C]∥Applied Imagery Pattern Recognition Workshop. Washington: IEEE, 2007:3-8.

[6]CHO P, SNAVELY N. Enhancing Large Urban Photo Collections with 3D LiDAR and GIS Data[J]. International Journal of Remote Sensing Applications, 2013, 3(1): 1-10.

[7]CHO P, SNAVELY N. 3D Exploitation of 2D Ground-level& Aerial Imagery[C]∥IEEE Applied Imagery Pattern Recognition Workshop. Washington, DC: IEEE, 2011:1-8.

[8]NI K, SUN Z, BLISS N. 3D Image Geo-Registration Using Vision-based Modeling[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing. Prague: IEEE, 2011:1573-1576.

[9]WENDEL A, IRSCHARA A, BISCHOF H. Automatic Alignment of 3D Reconstructions Using a Digital Surface Model[C]∥IEEE Computer Society Computer Vision and Pattern Recognition Workshops. Colorado Springs: IEEE, 2011:29-36.

[10]WENDEL A, BISCHOF H.Visual Localization for Micro Aerial Vehicles in Urban Outdoor Environments[M]∥FARINELLA G M, BATTIATO S,CIPOLLA R. Advanced Topics in Computer Vision. London: Springer, 2013: 181-214.

[11]WENDEL A, MAURER M, BISCHOF H. Visual Landmark-based Localization for MAVs Using Incremental Feature Updates[C]∥2012 Second International Conference on 3D Imaging, Modeling, Processing, Visualization & Transmission. Zurich: IEEE, 2012:278-285.

[12]WENDEL A, IRSCHARA A, BISCHOF H. Natural Landmark-based Monocular Localization for MAVs[C]∥2011 IEEE International Conference on Robotics and Automation. Shanghai: IEEE, 2011:5792-5799.

[13]SHEN Yonglin, LIU Jun, WU Lixin, et al. Reconstruction of Disaster Scene from UAV Images and Flight-control Data[J]. Geography and Geo-Information Science, 2011, 27(6): 13-17. (沈永林, 刘军, 吴立新, 等. 基于无人机影像和飞控数据的灾场重建方法研究[J]. 地理与地理信息科学, 2011, 27(6): 13-17.)

[14]FRAHM J M, HEINLY J, ZHENG Enliang, et al. Geo-Registered 3D Models from Crowdsourced Image Collections[J]. Geo-spatial Information Science, 2013, 16(1): 55-60.

[15]ZHANG Liang, MA Hongchao, GAO Guang, et al. Automatic Registration of Urban Aerial Images with Airborne LiDAR Points Based on Line-point Similarity Invariants[J].Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 372-379. (张良, 马洪超, 高广, 等. 点、线相似不变性的城区航空影像与机载激光雷达点云自动配准[J]. 测绘学报, 2014, 43(4): 372-379.)

[16]LI Tianwen. Theory and Application of GPS[M]. Beijing: Science Press, 2003:92-93. (李天文. GPS原理及应用[M]. 北京: 科学出版社, 2003:92-93.)

[17]JIA Yunde. Machine Vision[M]. Beijing: Science Press, 2000:191-192. (贾云得. 机器视觉[M]. 北京: 科学出版社, 2000:191-192.)

[18]SZELISKI R. Image Alignment and Stitching: A Tutorial[J]. Foundations and Trends in Computer Graphics and Vision, 2006, 2(1): 1-104.

[19]FISCHLER M A, BOLLES R C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6): 381-395.

[20]NIKON. GPS Unit GP-1[EB/OL].[2014-06-28]. http:∥imaging.nikon.com/lineup/accessory/camera/gp-1/spec.htm.

[21]SOUTH GROUP. RTK Surveying System >>S82T[EB/OL].[2014-07-08]. http:∥www.southsurvey.com/public/xianxi.php?id=301. (南方测绘. RTK测量系统>>S82T[EB/OL].[2014]. http:∥www.southsurvey.com/public/xianxi.php?id=301.)

(责任编辑：宋启凡)

修回日期： 2015-05-21

First author： LIU Yingzhen (1981—), female, PhD, majors in the construction of 3D geographic information and human-computer interaction.

E-mail： liuyz@lreis.ac.cn

通信作者： 诸云强

Corresponding author： ZHU Yunqiang

E-mail： zhuyq@igsnrr.ac.cn