失重环境下人体心血管功能失调及对抗措施的仿真设计研究

刘 洋，冯 娜，张 曦，常小红，张国鹏，卢虹冰，吴小明

失重环境下人体心血管功能失调及对抗措施的仿真设计研究

刘 洋，冯 娜，张 曦，常小红，张国鹏，卢虹冰，吴小明

目的：研究失重/微重力环境引起的人体心血管功能失调及对抗措施仿真建模方法。方法：在分析失重/微重力环境对心血管系统影响及心血管系统模型建立过程的基础上，利用血液动力学分析方法对整体模型进行仿真设计。结果：心血管系统模型应包括心脏泵和血管树以及反射控制系统。而在失重/微重力环境下，人体静力学压力消失，血液重新分布，并由此会产生一系列的变化，针对这些变化，设计了血量减少、脑内压/颅内压匹配关系、静脉塌陷模型，并建立了下体负压和间断性人工重力等措施对心血管系统失调的对抗仿真模型。结论：数学模型可有效地模拟失重/微重力环境下心血管系统的响应，为失重环境下人体心血管功能失调及对抗措施的研究提出了一种经济、实用的方法。

心血管系统；下体负压；间断性人工重力；模型

0 引言

随着神舟系列飞船的成功发射、载人航天工程的顺利实施、空间站计划的逐步开展，失重/微重力环境引起的航天员心血管系统功能失调逐渐引起了人们的广泛关注。近年来，失重/微重力环境对航天员心血管系统的影响机理及相应防护措施的研究已成为当前航天领域的重要研究方向。长期暴露在失重/微重力环境会引起航天员立位耐力降低、运动耐力下降、骨质疏松及航天运动病，国内外学者已经作了系列相关研究，并对失重/微重力环境引起心血管系统功能失调提出了许多假说，但也有一系列问题尚未解决。

20世纪90年代，空间实验室的4次生命科学飞行为航天心血管系统的研究提供了新的数据。但由于航天飞行实验的机会少、费用高，大多研究仍采用地面模拟失重的方法。目前，地面模拟失重的方法主要包括基于人体的头低位卧床实验、基于动物的尾部悬吊大鼠实验等。对于地面人体实验，无创测量比较困难，且模拟失重环境与实际失重环境存在一定的差别；对于地面动物实验，实验动物一般为四肢动物，因此血液静力学压力梯度变化与人体相差较大。与上述实验方法相比，利用数学模型进行生理信号仿真是一种成本低、综合的实验方法。数学模型可作为实验的补充，解释航天实验中的观察结果[1]，对失重/微重力环境下的心血管功能失调研究具有重要意义。

数学模型建立在真实人体/动物实验的基础上，实验为模型的建立提供真实数据和假说基础；同时，在对模型进行有效验证的基础上，可获得实验很难或无法获得的数据，且可对实验得到的数据进行解释，对结论或假说进行验证，并进一步引导实验。可以说，数学模型和实验是相互补充、相互促进的。目前，模拟特殊重力环境下心血管系统响应的数学模型有很多，如模拟+Gz加速度[2]、下体负压[3-4]（lower body negative pressure，LBNP）、头高/低位倾斜[5]、对抗措施[6]等的作用，但模拟失重环境下心血管系统响应的报道还很少。为此，本文首先分析失重/微重力环境对心血管系统的影响及防护，并在介绍建立一般心血管模型方法的基础上，进一步探讨失重/微重力环境下人体心血管模型的建立。

1 失重对心血管系统的影响及防护措施的研究现状

1.1 失重对心血管系统的影响

在失重/微重力环境下，血液静力学压力消失，造成体液头向转移，血液重新分布。同时，失重/微重力环境，引起反射性多尿，造成血量减少，易引起下肢静脉的顺应性降低、心脏萎缩等心血管系统的一系列变化。虽然失重/微重力环境对心血管系统造成了系列影响，但在航天飞行过程中航天员对这些适应性改变无明显异常表现。当航天员返回地球表面（1 Gz重力环境）时，普遍出现心血管功能失调，引起立位耐力不良，直接威胁航天员着陆后即刻的应急离舱能力，以及返回后对地球重力环境的再适应能力。目前，国内外学者已对航天飞行后心血管功能失调的发生机制进行了深入的研究，但仍有系列问题尚未解决，现已逐渐意识到整个机制相当复杂，除血量减少外，心脏与动脉血管的一系列适应性改变可能是另一项重要机制[7]，如血管结构与功能的改变[8]、血管重塑[7]、脑动脉与脑血流动力学变化[9]、颅内压与眼内压变化不匹配[10]、静脉特性的变化[11]等。

1.2 失重/微重力的防护

失重/微重力会对人体产生一系列影响，在航天飞行的初期，一般采用套带减轻体液转移导致的急性适应期症状。对于长时间的航天飞行，一般采用运动、水盐补充、LBNP和间断性人工重力等措施对抗失重对肌肉、骨骼、心血管（体液）等系统的不良影响。LBNP通过在下肢外部施加一个负压力，对抗失重/微重力环境下的血液头向转移，从而抗衡血液再分布影响。间断性人工重力是指在航天过程中每天给航天员施加一段时间的重力，实验结果表明其对心血管功能失调具有独特预防效果[12]，但由于在整个航天过程中施加人工重力需要巨型旋转轮，目前的技术尚无法实现。

总之，失重/微重力环境对人体心血管系统的影响是长时、持续的，暴露在失重/微重力环境时间越长，症状表现越明显。随着我国空间站的逐步建立及中长期航天飞行的逐步实现，航天员在太空中的时间越来越长，如何明确失重/微重力环境下心血管失调的机理，并进行针对性的防护，是保证我国航天事业稳步发展、保障航天员身体健康的关键问题。

2 心血管系统模型的建立

自从1957年J R Womersley[13]分析弹性血管的血流特性开始，人体心血管系统的数学模型开始迅速发展。从力学角度看，循环系统是由一个由泵（心脏）及黏弹性管道（血管系统）构成的流体管系，其内是具有一定黏性系数的非牛顿液体。在线性化假设的前提下，流体力学基本方程导出的传输方程，与电学网络中相应的网络方程和等效电路具有相同的形式（详见表1），因此可以用电学网络中的概念和方法解决流体力学中的问题。

表1 电学参量和生理学参量的等价关系

根据设计的目的不同，心血管系统模型的复杂性差别很大，主要包括两大类：集总参数模型和分布式模型。集总参数模型通常较为简单，只包括电阻和电容等基本组件，可以很好地描述压力系统与控制系统之间的相互作用，但却很难表达血液动力学参数在空间上的变化及分布。分布式模型相对复杂，包含多段血管树。每一个模型都有自己的特异性，根据研究目的建立模型，需要突出仿真的部位要细化，而不太关心的地方可以用简易模型来代替。一般来说，心血管系统可被视为包含2个主要模块的反馈系统：（1）压力系统，心脏被视为一个泵，负责收集静脉回心血液，向动脉泵血；（2）反射控制系统，它控制血压、心率和血流等的变化，使血压趋于稳定。

2.1 压力系统

压力系统主要包括心脏和血管。血管网络应包含动脉系统、静脉系统和外周循环系统。

心脏模型：人体心脏分为左心和右心2部分，分别驱动体循环和肺循环。在一个心动周期中，心室内压力和容积都会随时间发生变化。早期的研究主要使用斯塔林定律（Starling Law）来描述心脏输出量与回流充盈度，从而模拟心脏功能。之后，H Suga和K Sagawa[14]对狗的左心室进行研究，通过改变后负荷（外周阻力和动脉阻抗）和前负荷（舒张期容积）环境，提出了时变弹性模型，并利用时变弹性系数来描述心室压力-容积随时间变化的关系[15]。

血管的模拟：在给定血压梯度的情况下，可通过傅里叶变换和微分方程方法计算血管中血流随时间的变化[16]。J R Womersley[13]使用傅里叶变换的方法在一个血压梯度变化周期计算血管中的速度分布，但这种分布必须包含频率分量。之后，V C Rideout[17]提出使用微分方程的方法建立模型，很好地解决了血管顺应性的非线性问题，且该方法输入的血压梯度可以不是周期函数。

2.2 反射控制系统

人体心血管系统是一个可以自身调节的反馈控制网络，各段血管的血液动力学变化可以自身传递性调节。例如，由于主动脉的顺应性，随着血压的变化，顺应性会朝着相反的方向抑制血压发生突变，从而使血压不会特别高也不会特别低。

而非自身调节要受到神经反射调节的控制。颈动脉、主动脉和心肺压力感受器是心血管系统瞬时响应的主要传感器，如心率主要由颈动脉压力感受器控制，而其他感受器对其无影响[18]。为此，Katona提出了心率反馈调节模型，先计算出在颈动脉处血压偏离正常值时引起的压力感受器向神经中枢发放冲动的频率，然后计算该频率对心率的影响。而对于血管的顺应性，颈动脉压力感受器和心肺压力感受器都有一定的作用，而且只在瞬时产生作用，并没有持续影响[19]。J F Green和N C Miller[20]提出血管弹性控制模型，根据当次心动周期内平均颈动脉压偏离正常平均颈动脉压的值来计算顺应性的变化。

将压力系统（心脏和血管）模型和反射控制系统模型相结合，可将整个心血管模型构成一个闭环系统，如图1所示。根据连续性和守恒定律，可对各段血管压力和血流的相互关系和变化进行模拟。在模型的每个运算周期，由左心室开始，逐段计算各血管段的血压、血流、容积、阻力等参数。血液流经动脉系统、外周循环系统及静脉系统，随着血液回流至右心房，肺循环始于右心室，经过肺循环，血液流回左心房、左心室，并开始下一个周期的运算。

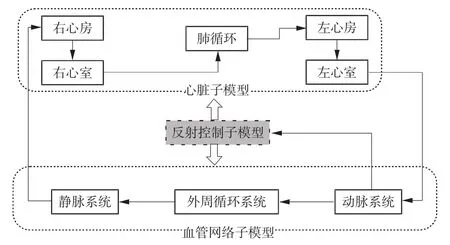
图1 心血管系统模型框图

3 失重/微重力环境下的建模

失重/微重力对人体的影响是一个长时间、缓慢作用的过程，很难进行完全的模拟，但国内外专家已对此进行了初步有益的研究。早期的研究主要是通过姿势改变模拟人体血液动力学响应。20世纪60年代，美国国家航空航天局借助空间实验室获得的数据，基于黑箱理论建立了失重/微重力环境下人体循环系统模型，该模型可根据血流量计算出循环系统的变量。Guyton模型曾被改进用于失重下体液调节及血量减少问题研究，后又进一步扩展用于研究立位应激下心血管系统的响应[21]。在此基础上，T Heldt等[22]建立了可对人体立位耐力不良进行仿真研究的模型。郝卫亚等[23]仿真研究了血量减少对立位应激时血压、心率和休克指数的影响。针对航天员返回地面后立位耐力不良的问题，J Broskey等[24]建立了简化的人体心血管系统仿真模型，模拟了28个生理参数的变化，从而描述心功能、血流阻力、跨壁压、血容量以及静脉顺应性。但上述模型大都是集总参数模型，且只能反映某些生理参数的变化。考虑到失重/微重力环境下心血管系统的影响，在建模过程中，需在传统的心血管模型中添加以下模块：

（1）血容量减少控制模块：失重时细胞外液的丢失和循环血容量的减少，是引起飞行后立位耐力不良的重要原因。一般认为，血量减少可引起循环系统平均充盈压降低，进而引起中心静脉压降低。中心静脉压降低会引起左心室舒张末期容积降低，经过心脏与外周的耦合作用导致血压的降低，心血管系统又通过压力反射作用代偿血压的下降以维持系统的稳定。因此，在血液循环过程中需引入血量改变的因素，并据此建立一个血量自身调节、控制模型。

（2）静脉血管塌陷模块：静脉血管的模拟与动脉血管类似，但由于静脉的血管壁较薄，且内部压力较低，容易发生塌陷。尤其是失重/微重力环境会引起人体血液头向分布，易引起下肢静脉塌陷。一旦静脉中的血压低于一定值，静脉血管就会塌陷，使血管的横截面发生变化。为此，M F Synder和V C Rideout[25]提出利用恒定周长的椭圆来表示发生形变的血管横截面，并得到了较好的仿真结果。

（3）颅内压和眼内压控制模块：近期的研究发现长时间航天飞行会引起航天员眼球变扁及视盘水肿[10]。目前，视觉和脑循环对长时间失重/微重力环境的适应性变化的机制尚不明确，可能与颅内压/眼内压的不匹配有关。颅内压模型已很成熟，S A Stevens等[26]提出了适用于失重/微重力条件下颅内压研究的集总参数模型，增加了颅内压与脑脊液、脑血流之间的调节关系来反映失重/微重力引起脑脊液和脑血流的变化对颅内压的影响。但关于眼内压的模型还比较少，近期，B S Gardiner等[27]针对眼部手术建立了眼部模型，仿真了房水产生、分布和吸收的过程及其与颅内压之间的关系，并预测了手术过程中最大颅内压。如何将颅内压和眼内压模型与心血管系统模型相结合，从而模拟失重/微重力对颅内压和眼内压的影响以及引起眼球形状等的变化，是目前仿真研究亟待解决的问题。

4 对抗措施的模拟

目前，失重/微重力引起心血管功能失调的有效对抗措施主要有LBNP和间断性人工重力。利用数学模型，可对这2种对抗措施进行仿真，判定2种措施的有效性，并研究不同的LBNP压力和持续时间及间断性重力的持续时间和时间间隔对防护心血管功能失调的效果，从而制订最佳的防护方案。

LBNP通过在下肢外部施加一个负压力，对抗失重/微重力下的血液头向转移。LBNP的施加会使下肢血管段的血压产生一个偏移量，从而引起人体全身血液分布的变化，这个过程可以用J Lundvall[28]的模型来模拟。

间断性人工重力是指在航天过程中每天给航天员施加一段时间的重力，这就需要模型必须为长时模型，并利用心率来计算时间，即每天要施加多少个心动周期的人工重力，并在特定的心动周期内增加血液静力学分量，从而模拟间断性人工重力对心血管系统的影响。

5 讨论

本文分析了建立心血管系统的基本理论与方法，并着重分析了建立失重/微重力环境下心血管系统模型的特殊性。一个完整的心血管系统必须包含动脉树、静脉回流、心脏模块和反射控制模块。考虑到失重/微重力环境的特殊性，模型中还需包含血量控制、静脉塌陷和长时的反射控制模块。

通过模型，实验结果可以更好地得到解释；通过实验，模型可以更加确切地模拟人体心血管系统。随着模拟技术与航天及地面实验相结合，失重/微重力环境下人体心血管系统的变化机理一定会得到更加合理的解释，人类可以健康地在太空中航行。

[1]White R J，Blomqvist C G.Central venous pressure and cardiac function during spaceflight[J].J Appl Physiol，1998，85（2）：738-746.

[2]LU H B，BAI J，ZHANG L F.Simulating study of cardiovascular response and+Gz protection afforded by extended coverage G-suit[J]. Space Med Med Eng，1998，11（4）：240-244.

[3]Melchior F M，Srinivasan R S，Thullier P H，et al.Simulation of cardiovascular response to lower body negative pressure from 0 mmHg to -40 mmHg[J].J Appl Physiol，1994，77（2）：630-640.

[4]Melchior F M，Srinivasan R S，Clère J M.Mathematical modeling of the human response to LBNP[J].Physiologist，1992，35（Suppl 1）：S204-S205.

[5]Stevens S A，Lakin W D，Penar P L.Modeling steady-state intracranialpressuresinsupine，head-downtiltandmicrogravityconditions[J]. Aviat Space Environ Med，2005，76（4）：329-338.

[6]Simanonok K E，Srinivasan E E，Myrick R S，et al.A comprehensive guyton model analysis of physiologic responses to preadapting the blood volume as a countermeasure to fluid shifts[J].J Clin Pharmacol，1994，34（5）：440-453.

[7]ZHANG L F，YU Z B，MA J，et al.Peripheral effector mechanism hypothesis of postflight cardiovascular dysfunction[J].Aviat Space Environ Med，2001，72（6）：567-575.

[8]Buckey J C Jr，Lane L D，Levine B D，et al.Orthostatic intolerance after spaceflight[J].J Appl Physiol，1996，81（1）：7-18.

[9]SUN X Q，YAO Y J，YANG C B，et al.Effect of lower-body negative pressure on cerebral blood flow velocity during 21 days head-down tilt bed rest[J].Med Sci Monit，2005，11（1）：CR1-CR5.

[10]Mader T H，Gibson C R，Pass A F，et al.Optic disc edema，globe flattening，choroidal folds，and hyperopic shifts observed in astronauts after long-duration space flight[J].Ophthalmology，2011，118（10）：2 058-2 069.

[11]Bleeker M W，De Groot P C，Pawelczyk J A，et al.Effects of 18 days of bed rest on leg and arm venous properties[J].J Appl Physiol，2004，96（3）：840-847.

[12]ZHANG L F，CHENG J H，LIU X，et al.Cardiovascular changes of conscious rats after simulated microgravity with and without daily-Gx gravitation[J].J Appl Physiol，2008，105（4）：1 134-1 145.

[13]Womersley J R.An elastic tube theory of pulse transmission and oscillatory flow in mammalian arteries[M].Dayton，USA：Wright Air Development Center，1957.

[14]Suga H，Sagawa K.Instantaneous pressure-volume relationships and their ratio in the excised，supported canine left ventricle[J].Circ Res，1974，35（1）：117-125.

[15]Suga H，Sagawa K，Demar L.Determinants of instantaneous pressure in canine left ventricle[J].Circ Res，1980，46（2）：256-263.

[16]Chao J C，Hwang H C.A review of the bases for the hydraulic transmission line equations as applied to circulatory system[J].J Biomech，1972，5（2）：129-134.

[17]Rideout V C，Dick D E.Difference-differential equations for fluid flow in distensible tubes[J].IEEE Trans Biomed Eng，1967，14（3）：171-177.

[18]Johnson J M，Rowell L B，Niederberger M，et al.Human splanchnic and forearm vasoconstrictor response to reductions of right atrial and aortic pressure[J].Circ Res，1974，34（4）：515-524.

[19]Samueloff S F，Browse N L，Shepherd J T.Respose of capacity vessels in human limbs to head-up tilt and suction on lower body[J].J Appl Physiol，1966，21（1）：47-54.

[20]Green J F，Miller N C.A model describing the response of the circulatory system to acceleration stress[J].Ann Biomed Eng，1973，1（4）：455-467.

[21]Srinivasan R S，Leonard J I，White R J.Space biology and medicine：humans in spaceflight[M].Reston，USA：American Institute of Aeronautics and Astronautics，1996：559-594.

[22]Heldt T，Eun B S，Roger D K，et al.Computational modeling of cardiovascular response to orthostatic stress[J].J Appl Physiol，2002，92（3）：1 239-1 254.

[23]郝卫亚，白净，张立藩，等.失重后血量减少致立位应激时心血管反应改变的仿真研究[J].生物医学工程学杂志，2002，19（1）：48-

（►►►►）（◄◄◄◄）52.

[24]Broskey J，Sharp M K.Evaluation of mechanisms of postflight orthostatic intolerance with a simple cardiovascular system model[J].Ann Biomed Eng，2007，35（10）：1 800-1 811.

[25]Synder M F，Rideout V C.Computer simulation studies of venous circulation[J].IEEE Trans Biomed Eng，1969，16（4）：325-334.

[26]Stevens S A，Lakin W D，Penar P L.Modeling steady-state intracranialpressuresinsupine，head-downtiltandmicrogravityconditions[J]. Aviat Space Environ Med，2005，76（4）：329-338.

[27]Gardiner B S，Smith D W，Coote M，et al.Computational modeling of fluid flow and intra-ocular pressure following glaucoma surgery[J]. PLoS One，2010，5（10）：e13 178.

[28]Lundvall J，Bjerkhoel P，Ivarsson C，et al.Dynamics of transcapillary fluidtransferandplasmavolumeduringlowerbodynegativepressure[J]. Acta Physiol Scand，1993，147（2）：163-172.

（收稿：2015-01-05 修回：2015-04-26）

Simulation design of cardiovascular dysfunction induced by weightlessness and countermeasures

LIU Yang1,FENG Na2,ZHANG Xi1,CHANG Xiao-hong1,ZHANG Guo-peng1,LU Hong-bing1,WU Xiao-ming1
（1.School of Biomedical Engineering,the Fourth Military Medical University,Xi'an 710032,China; 2.Teaching and Research Section of Physiology,Department of Basic Medicine, the Fourth Military Medical University,Xi'an 710032,China）

ObjectiveTo investigate the design and method for simulating the cardiovascular dysfunction induced by weightlessness and corresponding countermeasures.MethodsThe mathematical model was designed using hemodynamic method based on the analysis of the effect of weightless on cardiovascular system and the general process to establish cardiovascular model.ResultsIn general,the cardiovascular model should contain heart,vascular tree,and reflection system. In the weightless or microgravity environment,the hydrostatic pressure disappeared and the blood re-distributed to result in a series of changes.To simulate these changes,the models were designed to simulate blood volume deficits,intraocular/intracranial pressure mismatch,and vein collapse.The model to simulate the countermeasures,such as lower body negative pressure and intermittent artificial gravity,was also established.ConclusionThe mathematical model can simulate the response of cardiovascular system to microgravity and may be an economical and practical method to investigate cardiovascular dysfunction and countermeasures.[Chinese Medical Equipment Journal，2015，36（7）：16-19，33]

cardiovascular system;lower body negative pressure;intermittent artificial gravity;model

R318；V7

A

1003-8868（2015）07-0016-05

10.7687/J.ISSN1003-8868.2015.07.016

军队青年项目（13QNP126）

刘 洋（1981—），男，博士，讲师，主要从事生理信号仿真方面的研究工作，E-mail：yliu@fmmu.edu.cn。

710032西安，第四军医大学生物医学工程学院（刘 洋，张 曦，常小红，张国鹏，卢虹冰，吴小明），基础部生理学教研室（冯 娜）

吴小明，E-mail：wxming@fmmu.edu.cn