基于微分进化-蚁群优化算法的潜航器航路规划

【信息科学与控制工程】

基于微分进化-蚁群优化算法的潜航器航路规划

高永琪，张毅

(海军工程大学 兵器工程系，武汉430033)

摘要：航路规划是包括新型巡航鱼雷和诱饵、远程布雷系统等潜航器完成指定任务的关键技术之一；为了解决蚁群优化算法在航路规划时存在的容易陷入局部最优、收敛速度慢等问题，引入了微分进化原理，对蚁群优化算法进行了改进，提出了微分进化-蚁群优化混合算法；该算法将微分进化的随机偏差扰动产生新个体的思想融入到蚁群优化算法中，对蚁群算法的信息素进行优化；最后以潜航器航路规划问题为实例，对改进后的混合算法进行了仿真研究；结果表明：提出的混合算法不仅能够得到更好的解，还能显著地提高算法的收敛速度。

关键词：航路规划；蚁群算法；微分进化；潜航器

收稿日期：2014-04-25

作者简介：高永琪(1968—)，男，博士，副教授，主要从事导航制导与控制研究。

doi:10.11809/scbgxb2015.01.028

中图分类号：TP301

文章编号：1006-0707(2015)01-0099-04

本文引用格式：高永琪，张毅.基于微分进化-蚁群优化算法的潜航器航路规划[J].四川兵工学报，2015(1):99-101.

Citationformat:GAOYong-qi,ZHANGYi.DifferentialEvolution—UUVRoutePlanningBasedonAntColonyOptimizationAlgorithm[J].JournalofSichuanOrdnance,2015(1):99-101.

DifferentialEvolution—UUVRoutePlanning

BasedonAntColonyOptimizationAlgorithm

GAOYong-qi,ZHANGYi

(DepartmentofWeaponryEngineering,NavalUniversityofEngineering,LPA,Wuhan430033,China)

Abstract:Route planning is one of the key technologies for underwater unmanned vehicle (UUV) to complete appointed task. In order to solve some defects of the ant colony optimization such as easily to fall into local optimum and slowly to converge, we put forward differential evolutions--ant colony optimization algorithm which is an improved ant colony algorithm. The new algorithm added random deviation to optimize the pheromone of ant colony algorithm and to improve the convergence speed. The simulation experiments with the improved ant colony optimization about UUV route planning were conducted. The results show that the new algorithm is not only able to get a better solution, but also can significantly improve the convergence speed.

Keywords:routeplanning;antcolonyalgorithm;differentialevolution;UUV

由于新概念巡航鱼雷和诱饵、远程布雷系统等新型潜航器的航行时间长、距离远，因而航路规划是其完成任务的关键技术之一。意大利学者MarcoDorigo通过模拟自然界中蚂蚁群体的觅食行为于1991年提出的蚁群算法[1,2]可用于航路规划中。该算法采用正反馈和分布式并行计算机制，具有很强的自学习能力和较好的鲁棒性，易于和其他算法相结合。但是基本蚁群优化算法在解决复杂优化问题时搜索时间长，收敛速度慢，并容易陷入局部最优。

受到达尔文“优胜劣汰、适者生存”的自然进化原理的启发，美国学者Storn和Price于1997年提出了模拟自然进化按概率演进的微分进化算法[3]。微分进化算法与其他进化算法相比，在解决复杂的全局优化问题方面的性能更加突出，过程也更加简单，并且该算法在收敛速度和稳定性方面都比其他几种随机算法要好[4-5]。因此本文将微分进化的随机偏差扰动产生新个体的思想融入到蚁群优化算法中，提出了基于微分进化-蚁群优化的混合算法，并将该混合算法运用于潜航器的航路规划中，通过仿真研究取得了良好的效果，验证了该算法的可行性和有效性。

1潜航器航路规划问题

1.1航路规划性能指标

潜航器航路规划是指在特定约束条件下，寻找一条从出发点到目标点，并且满足某种特定指标的最优航路[6]。具体来说，就是在综合考虑潜航器能源消耗(如电池能量)、到达时间、敌方威胁(如敌方布雷区)及航行区域地形(如水下地形的可导航性)等前提下，为潜航器规划出一条最优或者是最能满足要求以完成指定任务的航路。在所有航路规划的性能指标中，安全性能指标和能源性能指标最为重要，即威胁代价最小性能指标和能耗代价最小性能指标。

最小威胁代价性能指标为

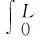
(1)

最小能耗代价性能指标为

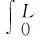
(2)

则潜航器航路规划的总性能指标为

minJ=gJt+(1-g)Jf

(3)

L为规划航路的长度；ωt表示航路上各点的威胁代价；ωf表示航路上各点的能耗代价，它们都是航路长度的函数；g∈[0,1]，表示安全性能与能源性能指标的权衡系数，其值可根据潜航器所执行任务的实际情况而定，如果潜航器任务重视航行时的安全性，则g选择较大的值，如果任务更多需要考虑潜航器的续航力，则g选择较小的值。由于潜航器能耗代价与航程成正比，为简化起见，仿真中取ωf恒等于1，因而Jf=L。

1.2威胁代价

当潜航器沿路径Lij航行时，N个威胁源对其产生的总威胁代价为

(4)

为了简化计算，如图1所示，把每条航路边分为10段，取其中的5个奇数点来计算这条边所受到的威胁代价，若威胁点到该边的距离在威胁半径之内，则按式(5)计算其威胁代价[7]

(5)

式(5)中：Lij为边ij的长度；d0.i,k表示该条边上的i/10分点距第k个威胁源中心的距离(i=1,3,5,7,9)；tk为第k个威胁源的威胁等级(图1)。

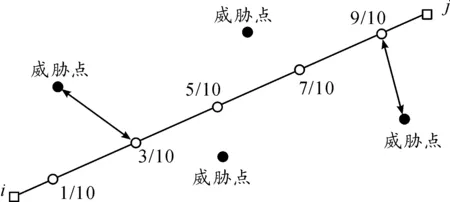
图1　航路威胁示意图

2微分进化-蚁群优化算法

由于蚁群优化算法存在容易陷入局部最优和收敛速度慢等不足，本文将微分进化原理中的随机偏差扰动产生新个体的思想融入到蚁群优化算法中，对蚂蚁留下的信息素进行优化，以期在航路规划过程中得到更好的信息素分布，从而获得更优的路径。通过对模拟地图进行直角网格划分，由当前点搜寻到下一个相邻点，直到搜寻到规划航路的终点，便形成连接起点和终点的规划航路。网格图中算法的数据结构是以当前点为中心的九宫图，共有8个相邻点，下一个点必须从以其为中心构成的8个点中选择，同时借鉴文献[8]设置可行域，其中网格大小d需根据实际问题规模进行合理设置。

2.1信息素

按照式(6)计算蚂蚁mk从节点i到节点j的转移概率

(6)

式(6)中：τj(t)为t时刻节点j上的信息素强度；ηj(t)为t时刻的启发式函数；α和β分别为信息素和启发式函数的影响系数；allowedmk为蚂蚁mk当前的可行域。这里启发式信息设置为航路的总性能指标J。

在蚂蚁构建航路的过程中，每完成一次迭代后，按式(7)对当前所构建的航路进行信息素的更新

(7)

2.2交叉算子

将蚂蚁分为若干相互独立的子群，子群数量记为ns。每个子群释放在路径上的信息素记为Γ={τi},i=1,2,…,ns。对于各蚂蚁子群当前的信息素，按照式(8)产生变异后的信息素分布

νi=τr1+F(τr2-τr3)i=1,2,…,ns

(8)

式中：τr1、τr2、τr3是在所有的蚂蚁子群中随机选出的三个信息素矩阵，并且r1≠r2≠r3。F是加权系数，表示两个信息素矩阵差别的放大倍数。由此可知，当τr2、τr3之间的差向量较小时，意味着各子群的信息素收敛于最佳的信息素分布。

再利用微分进化算法的交叉操作，通过变异信息素分布νi和当前的目标信息素τi的结合以提高路径上信息素的多样性，以扩大蚂蚁的搜索范围。改进算法利用式(9)和式(10) 生成新的信息素矩阵：

(9)

(10)

2.3选择算子

每个子群中的蚂蚁按照其信息素矩阵τi计算蚂蚁转移概率，得到最优路径的总性能指标Jτ-min，并将其定义为信息素τi的适应度值。信息素的选择操作可表示为

(11)

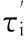
2.4算法实现步骤

微分进化-蚁群优化混合算法针对潜航器最优航路规划的运算步骤如下：

1) 参数初始化。对算法最大迭代次数Loop_max，蚂蚁数量M，参数α、β、ρ，微分进化算法参数F、CR，蚂蚁子群数量ns等参数进行设置，并将初始信息素τ0设置为一个常数；

2) 令迭代次数t=1，对各子群中的蚂蚁按照式(6)的转移概率进行路径构造，直到到达终点，当所有蚂蚁完成一遍路径构造后，按式(7)进行信息素更新；

3) 对各子群按式(8)进行变异操作，再按式(10)进行交叉操作，产生信息素矩阵μi；

4) 令t=t+1，各蚂蚁按信息素τi进行路径构造，并选出最小代价Jτ-min；

5) 各蚂蚁再按信息素μi进行路径构造，并选出最小代价记为Jμ-min；

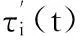
8) 对信息素进行更新。如果蚂蚁选择τi，则按照第4)步路径构造过程进行信息素更新；如果蚂蚁选择μi，则按照第5)步路径构造过程进行信息素更新；

9) 返回到步骤2)，直到t≥Loop_max时，算法结束并输出最优计算结果。

3仿真研究

为验证所提出的混合算法的有效性，利用Matlab7.0对该算法进行仿真实验。建立简易的模拟地图，设定潜航器的起点坐标为(0,0)，终点坐标为(100,100)，考虑了敌方的威胁区后，战场环境设置如表1所示。

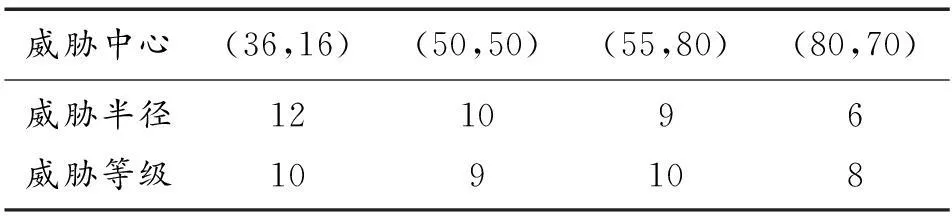
表1　环境设置

蚁群优化算法的参数和微分进化-蚁群优化混合算法的参数设置为相同的值，如表2所示。

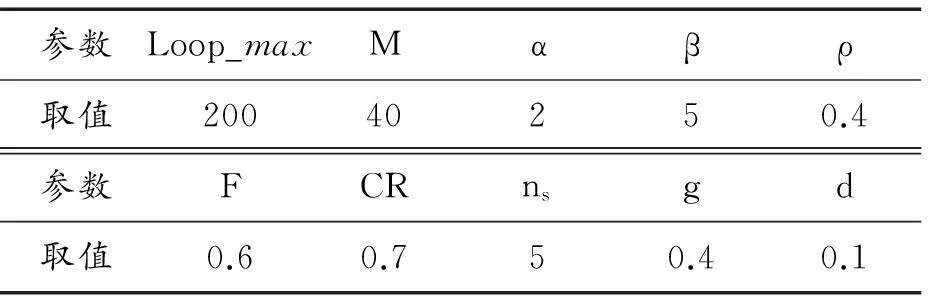
表2　参数取值

仿真结果如图2和图3所示。

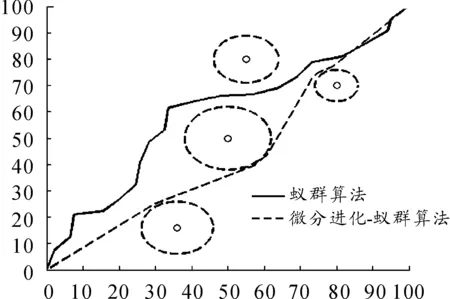
图2　规划航路

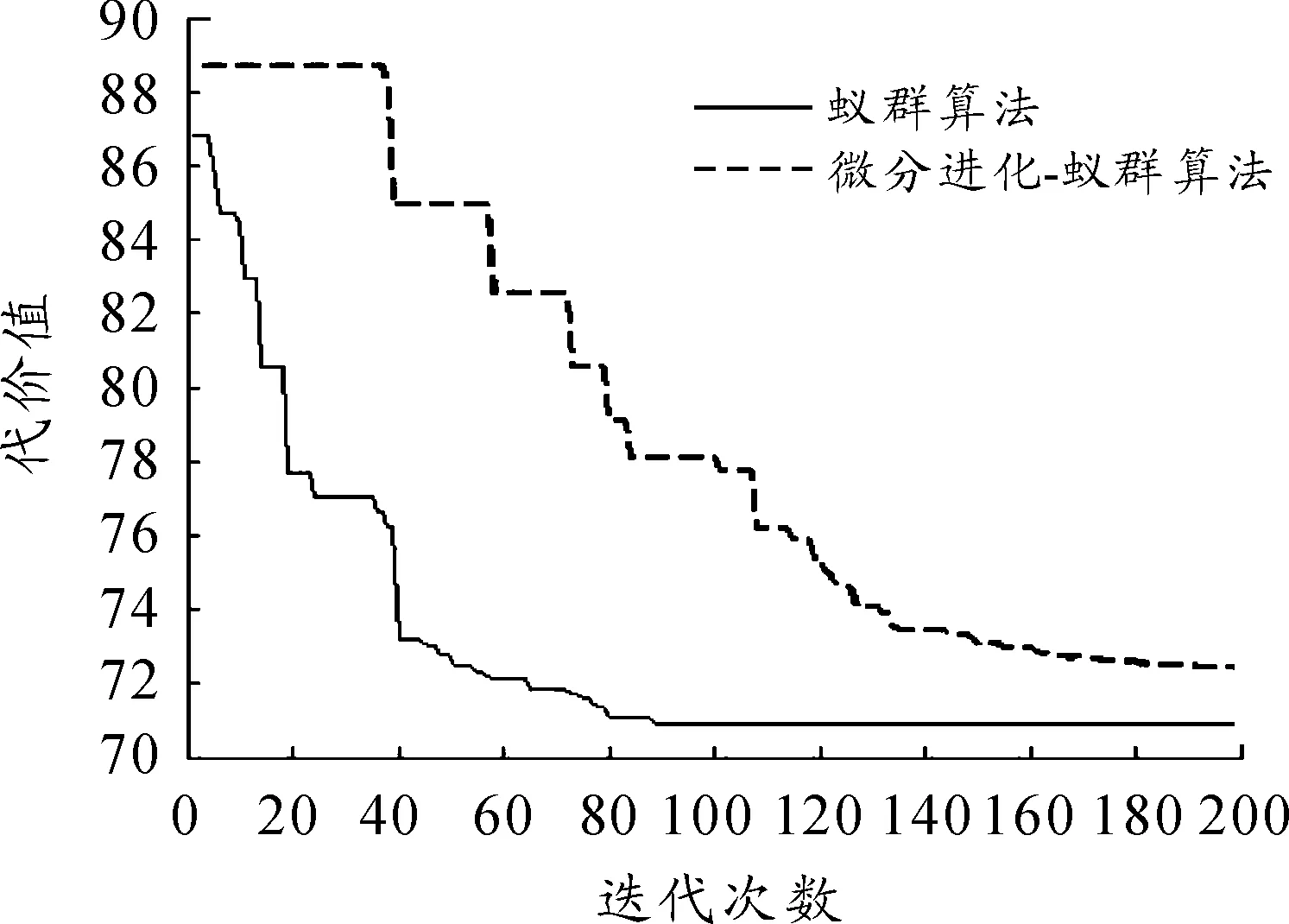
图3　收敛曲线

由图2和图3的仿真结果对比可知，微分进化-蚁群优化混合算法相对于蚁群优化算法不仅能够得到更优解(蚁群算法和混合算法都能避开威胁区，但混合算法的综合代价值更小)，而且其收敛速度也明显加快(蚁群算法收敛时迭代次数大约需要180次，而混合算法只需要90次左右)。

4结束语

针对潜航器最优航路规划问题，引入微分进化原理对蚁群优化算法进行了改进，提出了微分进化-蚁群优化混合算法，并用新的算法详细阐述了潜航器航路优化搜索问题，给出了算法的具体流程，最后进行了仿真验证。仿真结果表明：微分进化-蚁群优化混合算法比基本蚁群优化算法在潜航器航路规划中能够得到更优的结果和更快的收敛速度。

参考文献：

[1]DorigoM,GambardellaLM.AntColonySystem:ACooperativeLearningApproachtotheTravelingSalesmanProblem[J].IEEETransactionsonEvolutionaryComputation(S1089-778X),1997,1(1):53-66.

[2]MarcoDorigo,ThomasStützle.AntColonyOptimization[M].Brussels:MIT,2004.

[3]StornR，PriceK.Differentialevolution-asimpleandefficientheuristicforforglobaloptimizationovercontinuousspaces[J].JournalofGlobalOptimization，1997,11(4)：341-359.

[4]柯维，张永祥，吕博.基于微分进化算法的盲源分离[J].海军工程大学学报，2012，24(5):12-17.

[5]苏海军，杨煜普，王宇嘉.微分进化算法的研究综述[J].系统工程与电子技术，2008，30(9):1793-1797.

[6]高曼，刘以安，张强.优化蚁群算法在反舰导弹航路规划中的应用[J].计算机应用，2012，32(9):2530-2533.

[7]段海滨，张祥银，徐春芳等.仿生智能计算[M].北京：科学出版社，20011.

[8]张毅，高永琪，牛兴江．基于蚁群优化算法的水下航路规划[J]．鱼雷技术，2013，21(4)：272-276.

[9]刘志强，雷宇曜，阳再清. 基于元胞蚂蚁算法的防空靶机航路规划研究[J].兵工自动化，2014(5):4-6.

(责任编辑杨继森)