攻击角度约束的直升机载空空弹滑模中制导律
【装备理论与装备技术】
攻击角度约束的直升机载空空弹滑模中制导律
杨杨1,梁晓庚1,2,吴震1,张金鹏1
(1.中国空空导弹研究院, 河南 洛阳471009; 2.西北工业大学 自动化学院,西安710072)
摘要:基于虚拟目标的概念,设计了一种直升机载空空导弹滑模中制导律;首先,针对直升机载空空导弹在中末制导交接过程中,导弹低空飞行存在地物背景干扰及坠地等问题,提出了一种基于虚拟目标概念的弹道规划方案并给出了虚拟目标的计算公式;其次,基于变结构理论,选择导弹与虚拟目标的脱靶量及终端角度约束作为滑模面设计了制导律;最后,在MATLAB环境下进行仿真分析,并与最优制导律做比较,结果表明:提出的制导律具有更快的收敛速度,具有一定的工程实际意义,且该制导律易于理解,便于工程应用。
关键词:直升机载空空弹;中制导律;攻击角度;滑模变结构控制;虚拟目标
作者简介:杨杨(1984—),男,助理工程师,主要从事导航、制导与控制研究。
doi:10.11809/scbgxb2015.06.011
中图分类号:TJ765.3
文章编号:1006-0707(2015)06-0041-04
本文引用格式:杨杨,梁晓庚,吴震,等.攻击角度约束的直升机载空空弹滑模中制导律[J].四川兵工学报,2015(6):41-44.
Citationformat:YANGYang,LIANGXiao-geng,WUZhen,etal.MidcourseSliding-ModingGuidanceforAir-to-AirMissileonHelicopterwithInterceptAngle[J].JournalofSichuanOrdnance,2015(6):41-44.
MidcourseSliding-ModingGuidanceforAir-to-AirMissile
onHelicopterwithInterceptAngle
YANGYang1, LIANG Xiao-geng1, 2,WUZhen1, ZHANG Jin-peng1
(1.ChinaAirborneMissileAcademy,Luoyang471009,China;
2.SchoolofAutomation,NorthwesternPolytechnicalUniversity,Xi’an710072,China)
Abstract:A midcourse virtual target-based guidance was proposed to be applied for air-to-air missile on helicopter. First, the virtual target-based vertical trajectory programming technology was put forward to settle the long range low-altitude flight collision and the ground clutter abatement in the course of handover of guidance from the midcourse the terminal. Second, the miss distance between the missile and the virtual target which was derived by a new method were chosen as sliding mode and then the sliding mode control theory was employed to design the guidance law. Finally, representative simulation with MATLAB (Simulink) results and their analysis show preliminarily that the new guidance not only meets the requirement, but also converges quickly compared with the optimal guidance law. Furthermore this midcourse guidance law is easy to realize in engineering.
Keywords:air-to-airmissileonhelicopter;midcourseguidancelaw;angleofattack;sliding-modevariablestructurecontrol;virtual-target
武装直升机具备其他飞行器无法实现的空中悬停和低速机动能力,能够在地形复杂的环境下低空飞行。直升机载空空导弹主要用于对低空飞行的目标实施精确打击,一方面,近地条件下,复杂的地物背景对红外导引头截获目标十分不利,因此在中制导末端要求弹目视线角大于零,另一方面,导弹在低空、超低空飞行时容易坠地、因此研究带飞行高度和攻击角度约束的中制导律具有工程实际意义。
基于最优控制理论设计的制导律,能够满足终端约束条件和特定的性能指标,因此最优控制理论在带角度约束的制导律设计中得到广泛的应用。文献[1]针对固定或低速目标,推导了便于工程实现的广义弹道成型制导律。文献[2]针对时变系统,设计了解析形式的次优制导律。文献[3]则针对任意函数加权最优制导问题,研究了控制系统为一阶惯性环节和无惯性环节情形下最优制导律的设计问题。但上述提出的攻击角度约束制导律都是根据精确制导模型设计,而实际制导模型往往存在未建模动态和不确定性。滑模变结构控制对于参数摄动和外界干扰在一定条件下具有不变性,近年来在导弹制导控制中得到了广泛的应用。文献[4]针对再入机动弹头垂直打击目标的要求,采用最优滑模推导了具有落角约束的制导律。文献[5]针对电视制导侵彻炸弹,采用变结构反演方法设计带角度约束的制导律。文献[6]研究了考虑自动驾驶仪动态特性的制导律设计问题。
本文基于虚拟目标的概念,首先给出满足中制导性能指标的虚拟目标点,然后结合滑模变结构理论,设计了一种攻击虚拟目标点的滑模制导律,实现中制导段与末制导段的平稳交接。通过与最优制导律的比较,验证了本文提出的制导律的有效性。
1虚拟目标的计算方法
为了简化问题,做如下假设:将导弹和目标视为质点;导弹与目标始终在一个平面内运动;施加在导弹与目标上加速度矢量仅改变速度方向,导弹与目标的速度(大小)为已知常数,且VM>VT。图1所示为虚拟目标T′、目标T及导弹M相对运动关系。
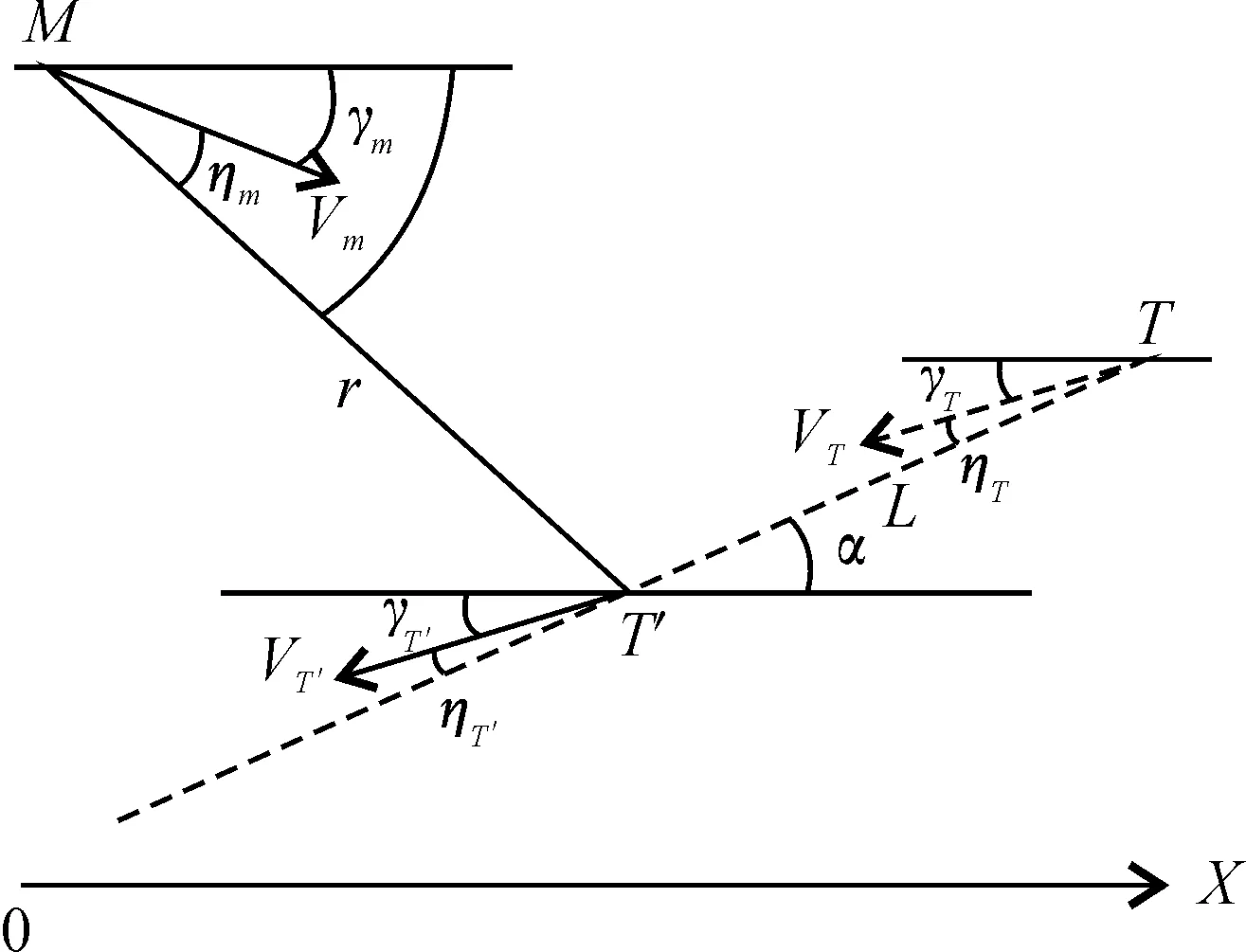
图1 虚拟目标、目标及导弹相对运动关系
其中:OX 为基准线;T 、T′及M表示目标、中制导虚拟目标和导弹;r 和λ 分别为导弹和虚拟目标的弹目相对距离和视线角;α 为虚拟目标和目标连线与基准线的夹角;L为虚拟目标与目标之间的距离;V、γ 和η 分别表示速度矢量、弹道倾角及前置角。
虚拟目标是人为引入的,因此虚拟目标的运动形式可以根据需要设置。为了简化问题,设置虚拟目标与目标具有相同的速度矢量,且虚拟目标满足如下约束:
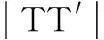
(1)
2) 导弹与虚拟目标之间的弹目视线角
(2)
2中制导问题的数学描述
图1给出了纵向平面内导弹虚拟目标相对运动几何关系,根据相对运动关系,其运动方程如下
(3)
(4)
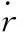
(5)
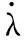
(6)
其中
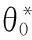
|λ(tf)-γM(tf)|<π/2
(7)
(8)
(9)
3终端角度控制制导律设计
对式(6)求导并将式(5)代入,整理得
(10)
式(10)中:AM和AT分别是导弹加速度和目标加速度。
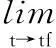
(11)
令式(10)的自适应滑模趋近率为
(12)
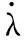
(13)
在实际工程中,目标横向加速度AT不易获得,不妨当作一个有界量,其界为
(14)
其中f表示AT的上界,由式(14)可得简化后制导律
(15)
对于式(15),如果选择切换系数ε = f + ζ > f, ζ =const> 0,则各个状态在有限时间收敛到滑动模态S=0。 因此,在制导律设计中只要选择合适的变结构项ε>f,就能保证制导系统稳定性,且K2越大收敛速度越快。
为了便于引用,把制导律式(15)简记为SMG。SMG中含有切换项,在实际工程应用中,控制量的切换存在一定的时间滞后,会造成抖动。为了降低抖动对实际系统的影响,可以对开关函数进行平滑处理,采用高增益连续函数x/(|x|+δ)替代开关函数sgn。另外,考虑中制导过程中θM是个小量,可以近似为cosθM,则SMG简化为
(16)
4实例仿真分析
在导弹可以获得精确的目标状态信息,无噪声干扰的情况下,对本文所推导的制导律在纵向平面内进行数字仿真验证,仿真初始条件为,中制导截获距离L=5 000m,截获角度α=0.01°。导弹在惯性坐标系的初始位置为rM1=0,rM2=300m,VM10=400m/s,VM20=0,初始速度倾角γM0=0;目标在参考惯性坐标系初始位置rT1=10 000m,rT2=100m,速度VT1=40m/s,VT2=0,目标在纵向平面保持匀速直线飞行,目标航迹角分别为γT0=175°、γT0=180°及γT0=185°。
为了进一步验证本文所设计制导律的性能,选择文献[8]提出的偏置比例导引(BPNG)进行仿真比较,BPNG制导指令为
在制导律SMG中,参数选取为k1=0.7,k2=1.5,ε=50,δ=0.01。通过数学仿真来检验变结构制导律的制导性能,仿真结果比较见表1、表2及表3及图2至图7。
表1和图2是在目标航迹γT0=175°的情况下,应用两种制导律的仿真结果比较和弹目相对运动轨迹。表2和图3是在目标航迹角γT0=180°的情况下,应用两种制导律的仿真结果比较和弹目相对运动轨迹。表3和图4是在目标航迹角γT0=185°的情况下,应用两种制导律的仿真结果比较和弹目相对运动轨迹。从图中可以看出,在目标航迹角γT0=175°、γT0=180°和γT0=185°的条件下,通过选择与之对应的和,可以得到不同的弹道曲线,且在弹道末端均达到设定的终端攻击角度和脱靶量要求。图5、图6及图7分别表示在目标航迹角γT0=185°的情况下,应用两种制导律导弹的视线角速率、视线角及过载的对比。结果表明,与偏置比例导引律相比,SMG使视线角误差及视线角速度以更快的速度收敛至平衡点,这样更有利于中末制导段平稳过渡。仿真结果同时表明,滑模制导律需要的过载更小,从而可以降低对执行机构的要求,有利于工程实现。
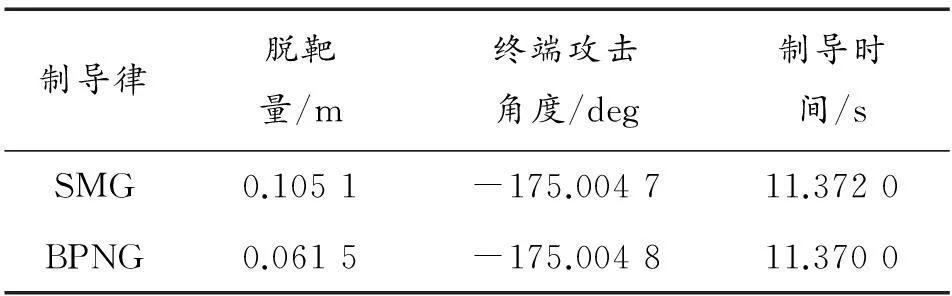
表1 目标航迹角 γ T(t f)=175°仿真结果比较
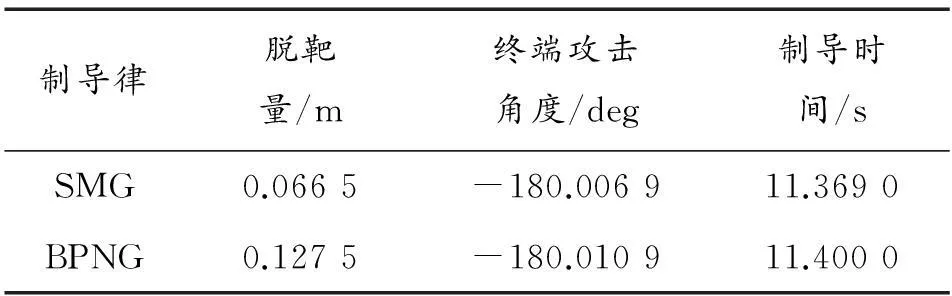
表2 目标航迹角 γ T(t f)=180°仿真结果比较
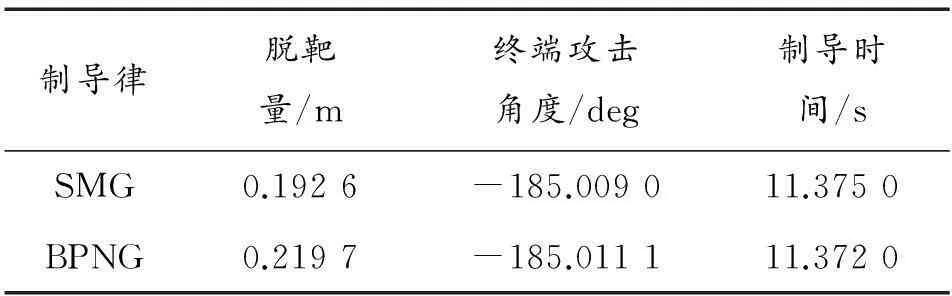
表3 目标航迹角 γ T(t f)=185°仿真结果比较
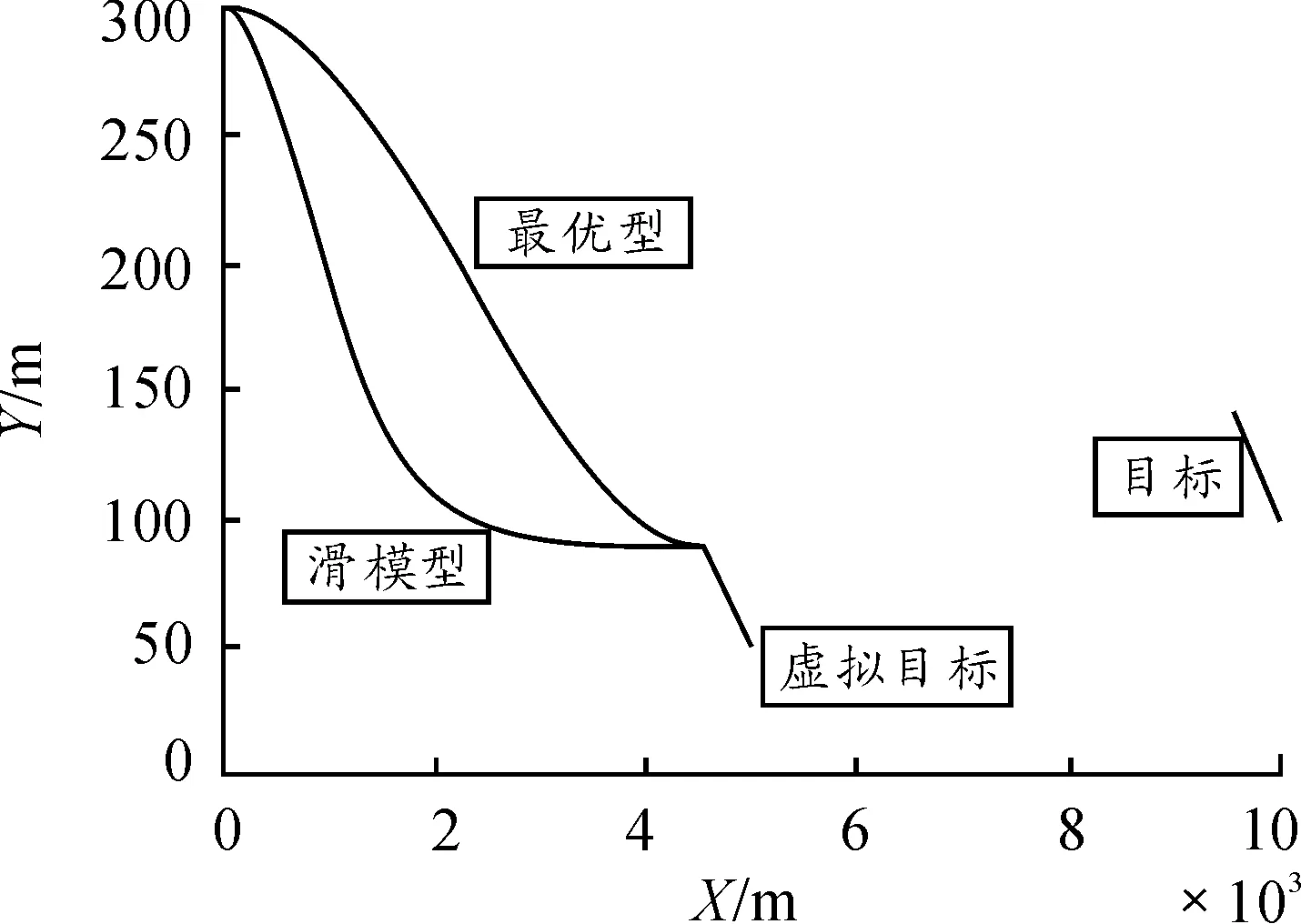
图2 γ T(t f)=175°纵向平面弹道曲线
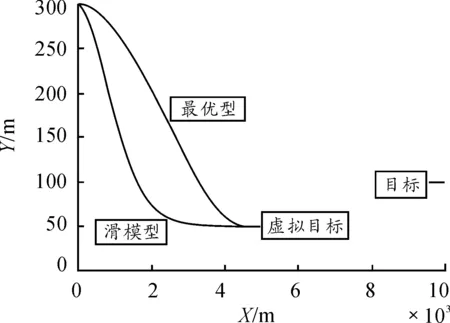
图3 γ T(t f)=180°纵向平面弹道曲线
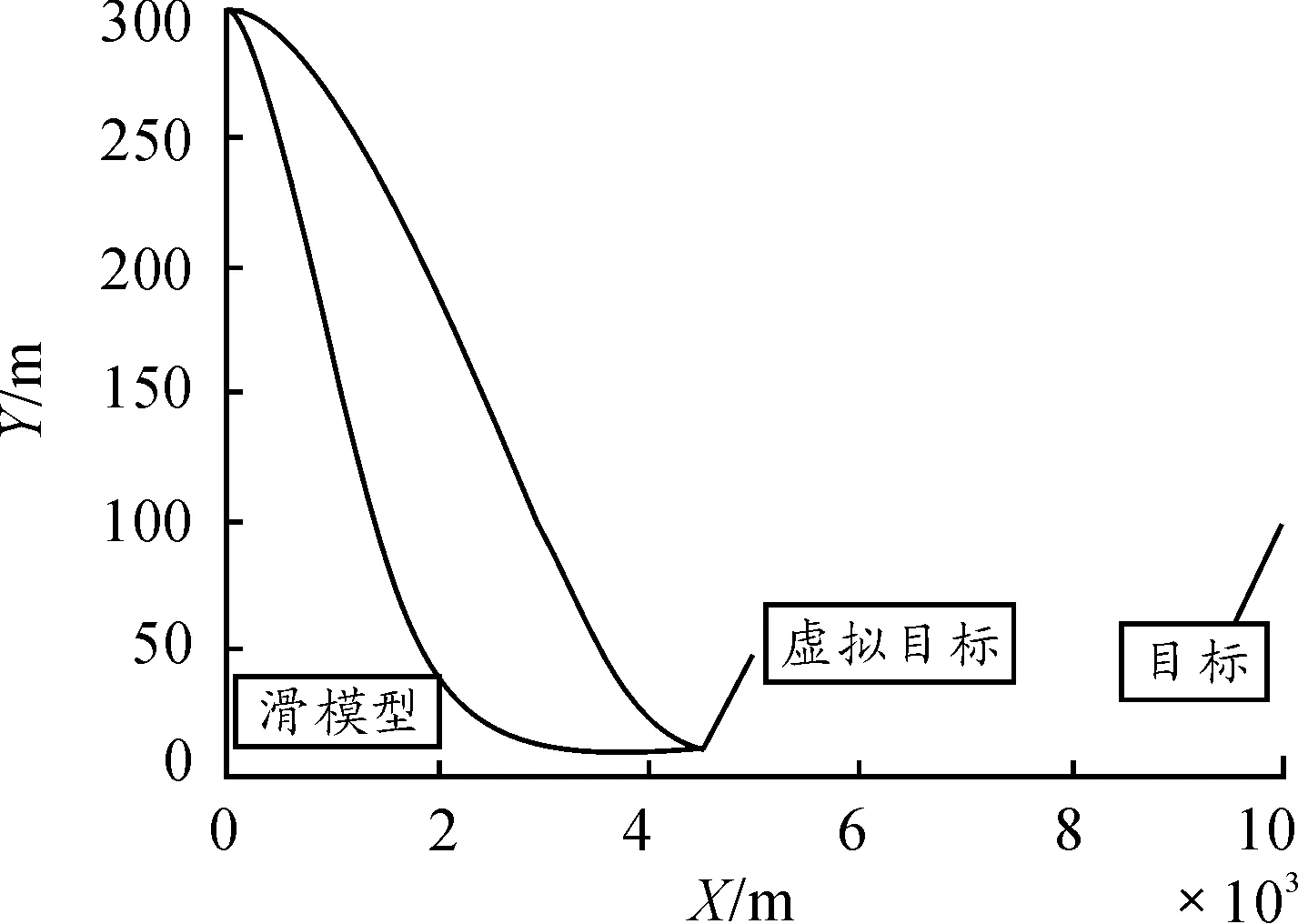
图4 γ T(t f)=185°纵向平面弹道曲线
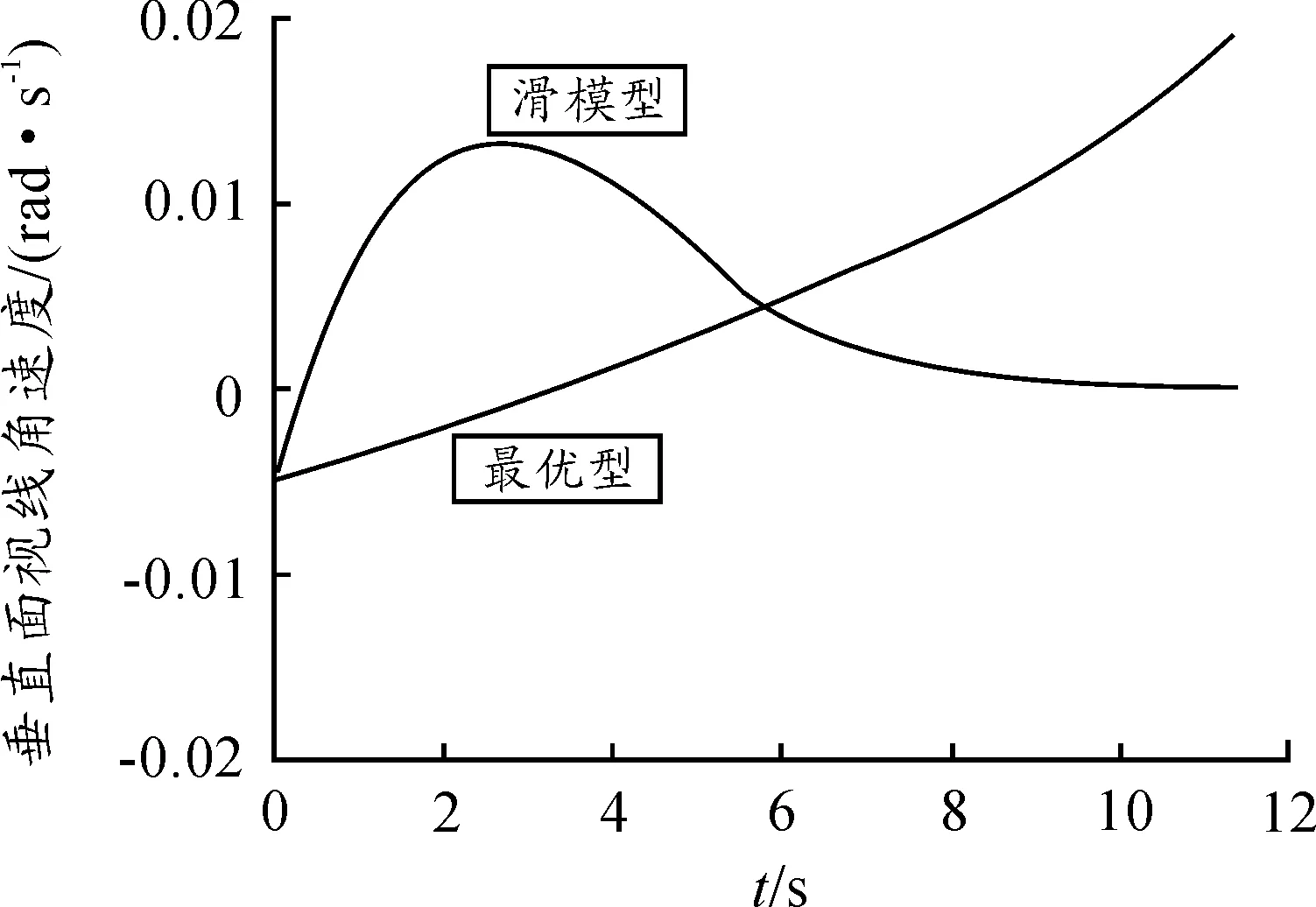
图5 γ T(t f)=185°纵向平面视线角速率变化曲线
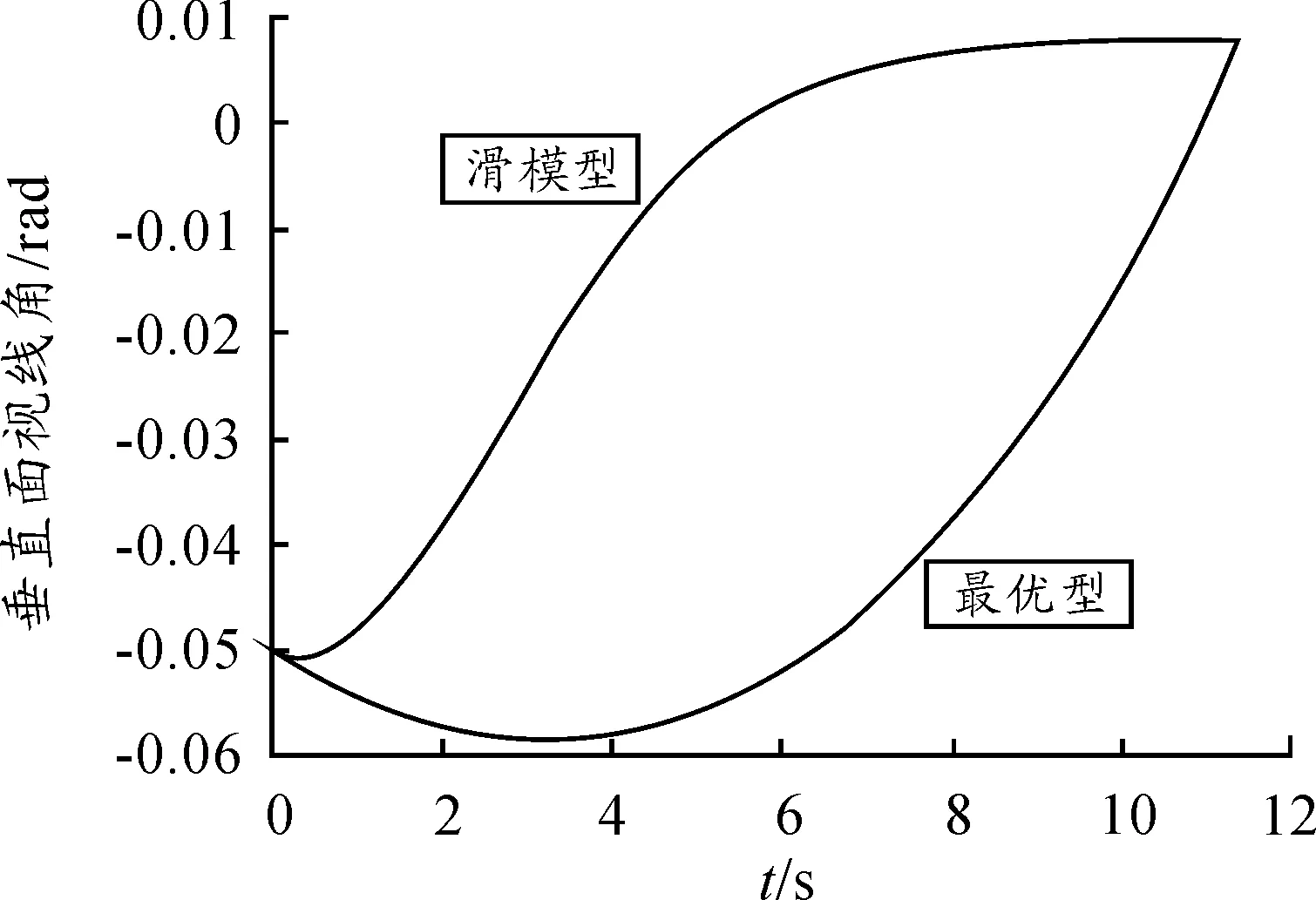
图6 γ T(t f)=185°纵向平面视线角变化曲线
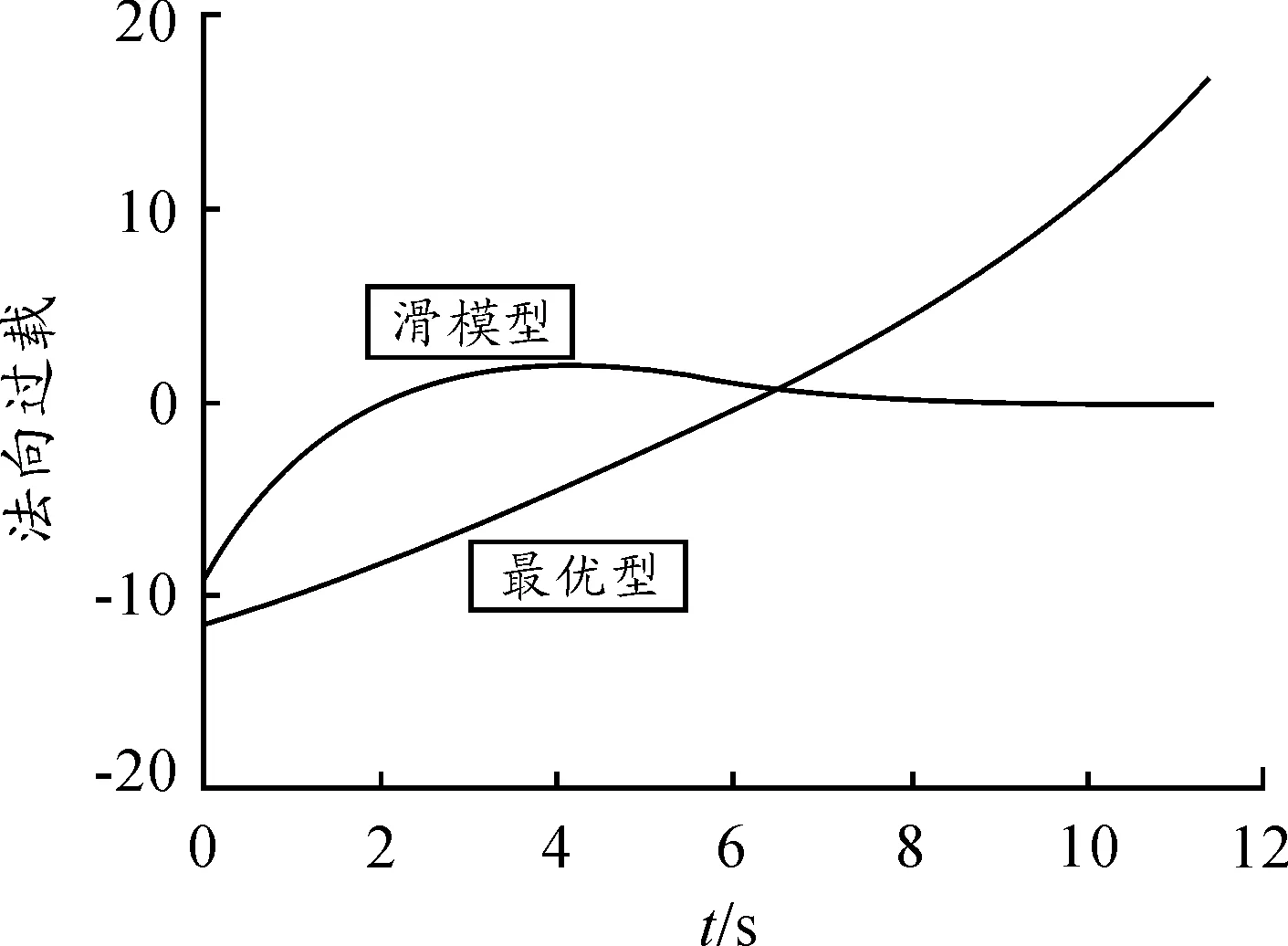
图7 γ T(t f)=185°纵向平面过载变化曲线
5结论
本文基于虚拟目标的概念,设计了一种直升机载空空导弹滑模中制导律。首先,基于虚拟目标的概念,设置了满足中制导性能指标的虚拟目标点;然后,根据导弹、虚拟目标的相对运动方程,结合本文提出的滑模制导律引导导弹去追踪虚拟目标点,从而解决直升机载空空导弹在低空、超低空飞行时的防坠地及中末制导交接过程中减少地物背景的干扰等问题;最后,仿真结果表明,与传统的偏置比例导引律相比,本文给出的滑模制导律收敛速度快,且该制导律物理过程清晰,便于工程实现。
参考文献:
[1]刘大卫,夏群利,崔莹莹,等.具有终端位置和角度约束的广义弹道成型制导律[J].北京理工大学学报,2011,31(12):1408-1413.
[2]窦磊,窦骄.带多约束条件的次最优中制导律[J].宇航学报,2011,32(12):2505-2509.
[3]张友安,黄诘,孙阳平.带有落角约束的一般加权最优制导律[J].航空学报,2014,35(3):848-856.
[ 4]胡正东,郭才发,蔡洪.带落角约束的再入机动弹头的复合导引律[J].国防科技大学学报,2008,30(3):21-26.
[5]贾庆忠,刘永善,刘藻珍.电视制导侵彻炸弹落角约束变结构反演制导律设计[J]宇航学报,2011,29(1):208-214.
[6]晁涛,王松艳,杨明.带角度约束的倾斜转弯飞行器制导律设计[J].弹道学报,2014,29(1):56-60.
[7]Byung Soo Kim,Jang Gyu Lee.Homing Guidance with Terminal Angular Constraint Against Nonmaneuvering and Maneuvering Target[C]//Journal of Guidance,Control,and Dynamics,1997-3474.
[8]Kim B S,Lee J G,Han H S.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.
(责任编辑周江川)

