小卫星太阳电池阵结构声振响应分析研究
张红亮,王海明,秦 江
(航天东方红卫星有限公司,北京 100094)
0 引言
在发射段,运载火箭产生的喷气噪声和气动噪声作用于卫星结构表面,产生比较恶劣的结构声振环境,特别是对高结构系数(结构面积与质量之比)的结构可产生高达50g的方均根响应加速度[1]。由于结构声振具备宽频域、随机性等特点,其理论预示方法一直备受国内外研究者的关注[2-6]。
小卫星太阳电池阵结构板一般是由上下厚度相同的碳纤维复合材料面板和中间的铝蜂窝芯子组成的夹层板结构。太阳电池阵由于表面积大、面密度小,通常是小卫星结构中对声振激励最为敏感的部件之一,因此在其研制过程中,一般采用力学环境试验手段考核结构强度、验证结构设计方案的 正确性。但在理论计算方面仍局限于利用有限元方法完成结构动力学响应分析。由于太阳电池阵在中高频区域的结构模态比较密集,模态参数表现出很大随机性,为正确描述高频模态振型,有限元分析时需要划分的网格非常密集,造成计算量呈指数增加,因此采用有限元方法分析太阳电池阵声振问题面临较大的困难。
本文基于统计能量分析(SEA)原理,建立典型小卫星太阳电池阵结构的统计能量分析模型。根据太阳电池阵结构板(碳纤维复合材料面板+铝蜂窝芯子)的特点,推导其SEA 参数,并计算结构板的声振响应。最后将分析结果与试验结果对比,以验证该声振响应分析方法的有效性。
1 统计能量分析理论
统计能量分析主要采用统计的手段分析耦合子系统在时域、频域和空间上的平均响应,在关心的分析频率带宽内,建立各理想子系统(梁、板、壳、声场等)的模型,计算各子系统的SEA 参数 模态密度、内损耗因子和耦合损耗因子,建立描述子系统能量损耗和传递的功率流平衡方程。各子系统平均能量可求解方程得到,进一步计算可得到其他动力学变量(如位移、速度、压力)的方均根值。统计能量分析的建模方法独特,虽然每个子系统的特性都是通过统计的手段得到,看起来比较“粗糙”,但其统计精度完全符合工程要求。
统计能量分析的建模方法是基于以下基本假设:保守弱耦合激励不相关,给定子系统在关注的分析频带内所有共振模态之间的能量等分,满足互易性定理[7]。根据以上假设将复杂的动力学系统划分为N个子系统,建成图1所示的统计能量分析模型。
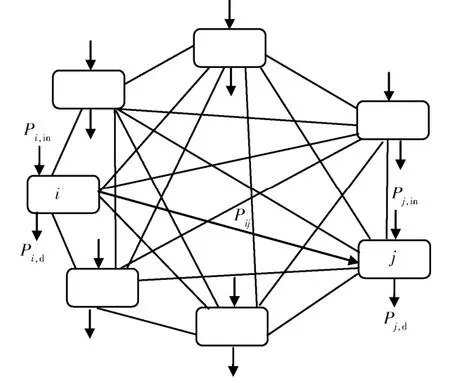
图1 统计能量分析模型 Fig.1 Statistical energy analysis model
每个子系统i的内部损耗功率为

其中内部损耗因子iη由阻尼损耗因子、结构声辐射损耗因子和边界连接损耗因子3 种因素之和构成。
子系统i到子系统j的纯功率流(双向)为
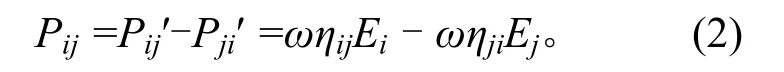
当振动为稳态振动时,功率流平衡方程为
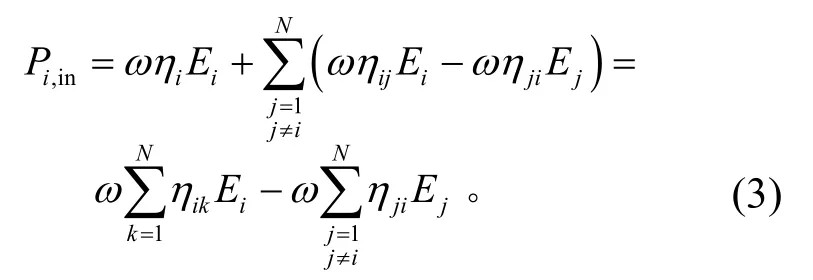
由于niηij=njη ji,可得到如下统计能量分析系统方程:
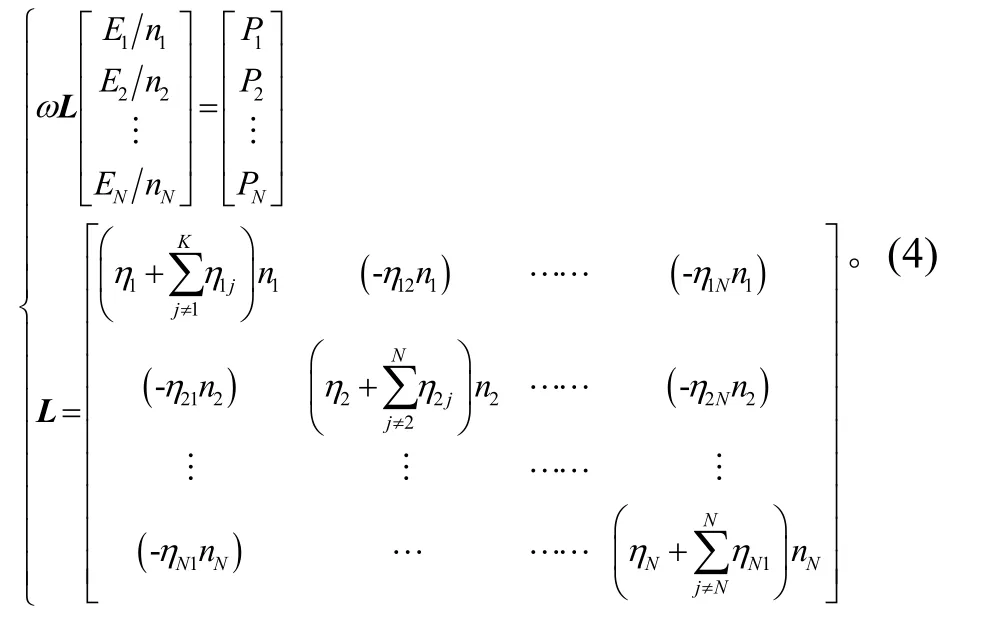
以上各式中:ω为频带的几何中心频率;ηij为子系统i到子系统j的耦合损耗因子;Ei,Ej分别为子系统i和j的振动能量;ni为子系统i的模态密度。
2 太阳电池阵结构统计能量分析建模
某小卫星太阳电池阵结构板的设计选用传统的碳纤维网格面板+铝蜂窝芯子的组合形式,尺寸为2000 mm×1200 mm×25.4 mm。统计能量分析建模时,将太阳电池阵结构板划分为1 个子系统,混响声场划分为2 个半无穷声场子系统,结构子系统在混响室与声场子系统耦合作用,引起结构宽频声振响应。结构板子系统有效质量主要由结构板和电池板及电路的质量组成。利用VAone 软件建立的太阳电池阵声振响应分析模型如2 所示。
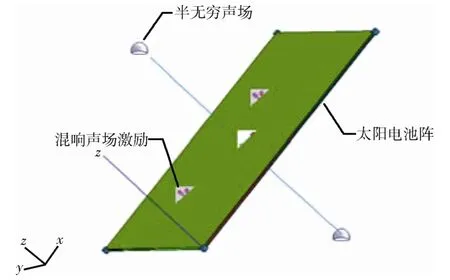
图2 太阳电池阵SEA 模型 Fig.2 SEA model of solar array panel
SEA 模型中,利用混响声场激励来表征声对结构的作用,半无穷声场用来表征结构对声场的作用,结构板系统采用蜂窝夹层板建模,面板假设为正交各向异性板。在上述建模基础上,进一步确定SEA 参数如下:
1)太阳电池阵结构模态密度
考虑到太阳电池阵是蜂窝夹层结构且面板为碳纤维复合材料,目前主流SEA 软件尚不支持该 结构板的建模。本文在计算太阳电池阵模态密度时采用公式[8-9]
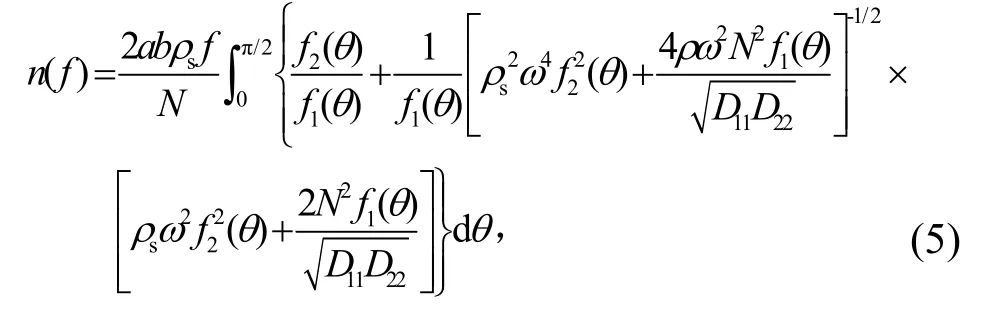
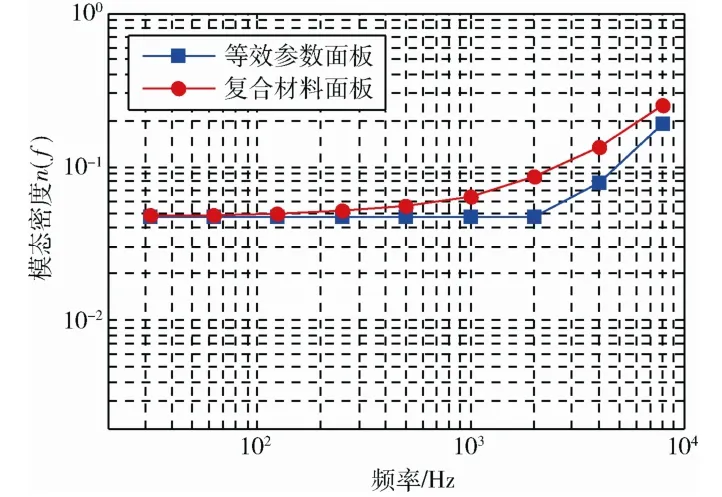
图3 太阳电池阵的模态密度 Fig.3 Modal density of solar array panel
由图3可以看出,等效参数面板与复合材料面板的模态密度在低频段几近重合,但在高频段开始出现差异。文献[10]利用基于输入点导纳法和试验数据所获得的铝蜂窝夹层板模态密度,与式(5)计算结果比较一致。
2)太阳电池阵结构声辐射系数
声辐射系数是描述结构与声振耦合作用的非常关键的参数,研究表明蜂窝夹层板的临界频率对其声辐射系数有很大的影响。对于铝蜂窝夹层板结构,其临界频率为
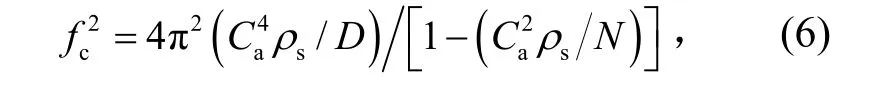
式中:D和N分别为夹层板的弯曲刚度和剪切刚度,ρs和Ca分别为结构板面密度和声速。由式(6)计算出小卫星太阳电池阵的临界频率为837 Hz,进一步得到其声辐射系数如图4所示。

图4 太阳电池阵的声辐射系数 Fig.4 Radiation factor of solar array panel
3)内损耗因子
SEA 中的内损耗因子等于结构的临界模态阻尼比的2 倍,它对随机响应的影响是比较显著的。目前大多数情况下结构内损耗因子的确定主要依据经验或试验结果。文献[11]利用基于频域小波变换的方法来识别铝蜂窝夹层板结构阻尼,其在低频段识别的结果为0.02~0.04。文献[12]利用功率输入法辨识铝蒙皮蜂窝夹层板结构内损耗因子全频段平均值为0.027。通常考虑声场对结构的影响时,子系统内损耗因子仍需加上结构声辐射损耗因子,这样总的损耗要比结构阻尼大很多。
4)混响声场对太阳电池阵的输入功率
混响声场产生的随机压力谱是以面载荷的形式作用在太阳电池阵表面的,此时可以把它看作是声场对板的激励。混响声场对板的输入功率可表示为
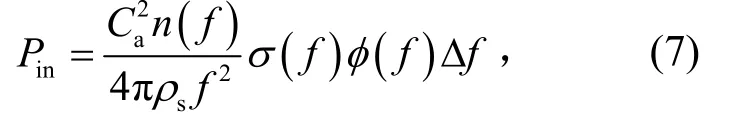
式中:φ(f)为混响声场压力谱;n(f)为太阳电池阵的模态密度;σ(f)为声辐射系数;ρs为结构板面密度;Ca和f为声速和频率;Δf为分析频率带宽。
太阳电池阵噪声试验量级如表1所示。按照表中的声压谱,根据式(7)计算的输入功率如图5所示。
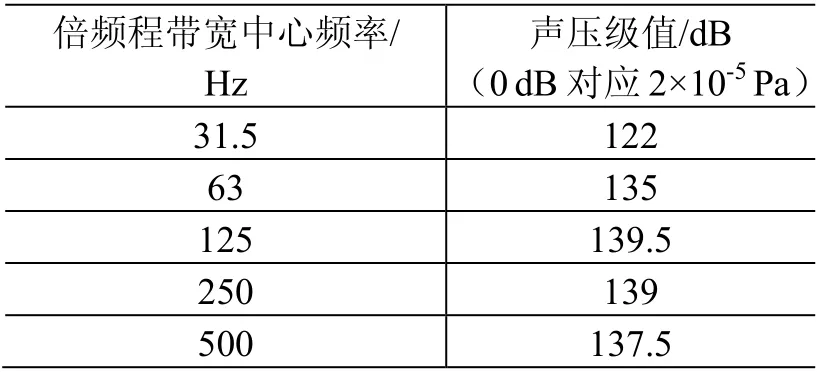
表1 噪声试验量级 Table1 Acoustic test level
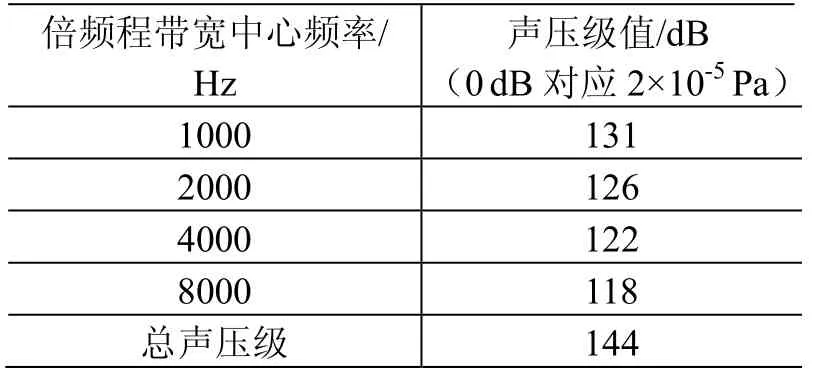
表1 (续)
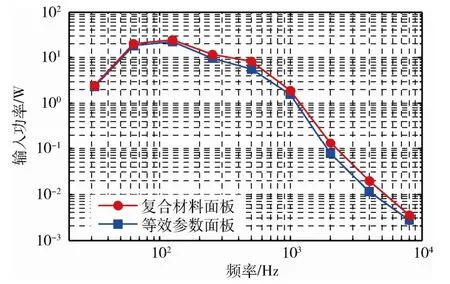
图5 噪声试验时的输入功率 Fig.5 Power input of acoustic test
根据式(7)和图5,可以看出,夹层板模态密度对声场输入功率估算有很大影响。等效参数面板建模得到的输入功率在高频段要明显小于复合材料面板建模的结果。
5)太阳电池阵的加速度响应
将太阳电池阵当作一个子系统进行求解,输入到板内的功率等于其消耗的功率,则太阳电池阵的功率平衡方程为

式中:η为子系统总的内损耗因子;E为子系统的振动能量。
太阳电池阵的加速度方均根响应为

式中,M为太阳电池阵子系统的有效质量。
若分别考虑声场和太阳电池阵子系统,则在求解太阳电池阵的响应时需建立声场模型并考虑结构的声辐射效应,式(8)变为
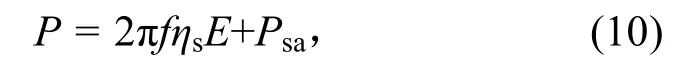
式中,Psa为结构到声场的传递功率,与结构声辐射系数和振动能量密切相关。
3 太阳电池阵结构声振试验响应分析
3.1 噪声试验
太阳电池阵噪声试验在混响室完成(见图6)。试验时,太阳电池阵夹层板共布置10 个三向加速度传感器(A1~A10),测点分布如图7所示。

图6 太阳电池阵进行噪声试验 Fig.6 Acoustic test of solar array panel
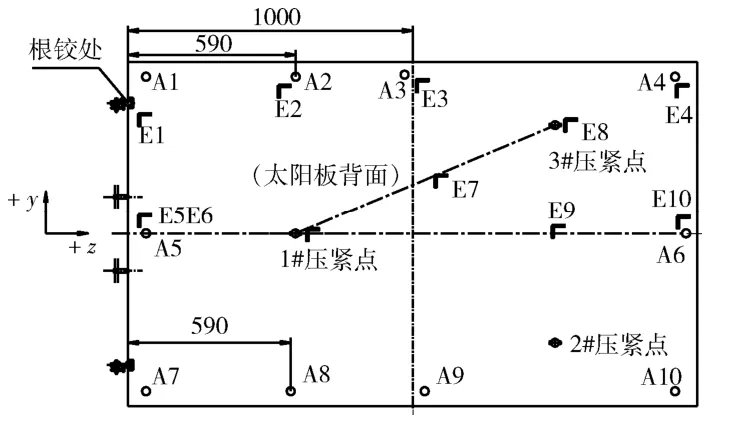
图7 加速度测点位置 Fig.7 Measurement location for acceleration test
3.2 分析与试验结果对比
3.2.1 模态密度影响分析
SEA 建模时,碳纤维网格面板分别采用等效参数面板和复合材料面板建模,结构总内损耗因子根据经验取0.05,加速度响应计算结果与试验结果对比如图8所示,其中:灰虚线为10 个测点的测量数据,黑实线为所有测量数据的平均值。可以看出,复合材料面板建模得到太阳电池阵加速度响应与试验平均结果吻合较好,而等效参数面板建模得到的响应在高频段偏小,这主要是由于等效参数面板建模的声场输入功率估计偏小造成的(见图5)。
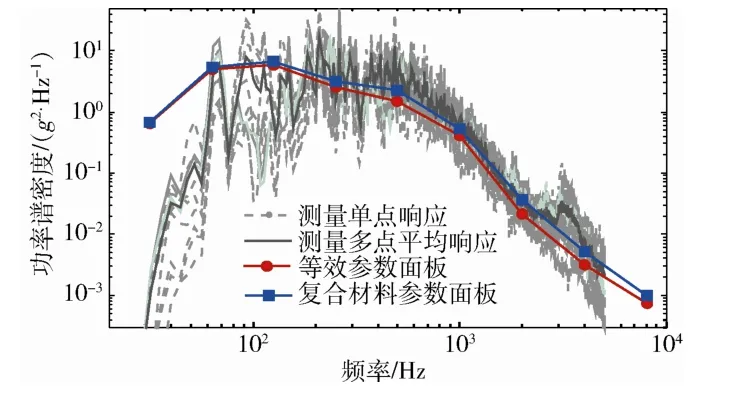
图8 不同模态密度下太阳电池阵声振响应计算与 试验结果对比 Fig.8 Comparison of analysis and test results for solar array vibro-acoustic response for different modal densities
3.2.2 内损耗因子影响分析
根据图2中的SEA 模型,只保留太阳电池阵子系统和混响声场激励。此时,结构的声辐射效应体现在式(8)的总内损耗因子中。分别取总内损耗因子为0.01、0.03、0.05、0.08 和0.2,根据式(9)计算得到噪声激励下太阳电池阵夹层板在31.5~8000 Hz 频率范围内的加速度响应如图9所示。由图9可知,内损耗因子对太阳电池阵噪声响应预示结果的影响是比较大的,其中,总内损耗因子取0.05 时的分析结果在高频段与试验测量平均功率谱密度曲线吻合非常好。
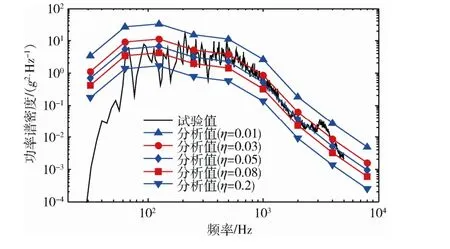
图9 不同内损耗因子下太阳电池阵声振响应计算与 试验结果对比 Fig.9 Comparison of analysis and test result for solar array vibro- acoustic response for different total damping losses
3.2.3 结构声辐射影响分析
图10给出了太阳电池阵结构阻尼损耗功率、声辐射损耗功率和总损耗功率对比曲线。可以看出,在临界频率附近声辐射损耗功率占主导地位,随着分析频率远离临界频率,太阳电池阵阻尼损耗功率逐渐占据主导。事实上,声辐射损耗功率可与结构阻尼损耗功率综合考虑,并以总内损耗因子参数表征。图11给出了总内损耗因子建模与声辐射损耗因子+阻尼损耗因子建模的计算结果对比,其中,总内损耗因子取0.05,阻尼损耗因子取0.02。可以看出,有无声辐射损耗因子的2 种建模方法其计算结果与试验结果基本吻合,其中声辐射建模方法在临界频率附近估值偏小,但两者预示总方均根值一致。
为便于量化比较,表2给出以上各分析工况及试验得到的太阳电池阵加速度总方均根响应值。
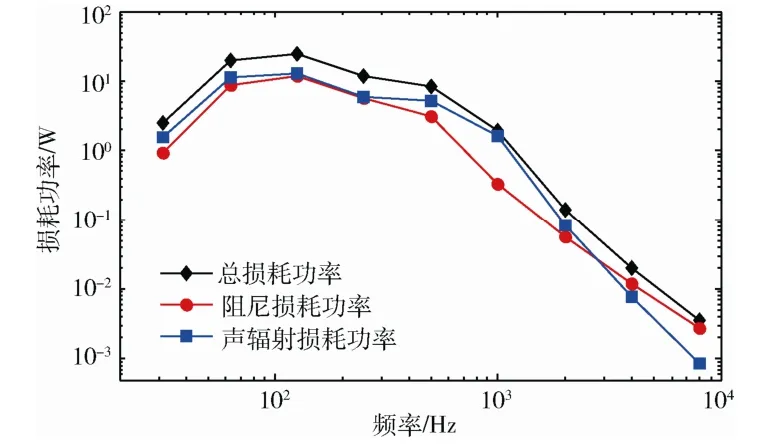
图10 太阳电池阵各种损耗功率对比 Fig.10 Comparison of various power losses of solar array panel
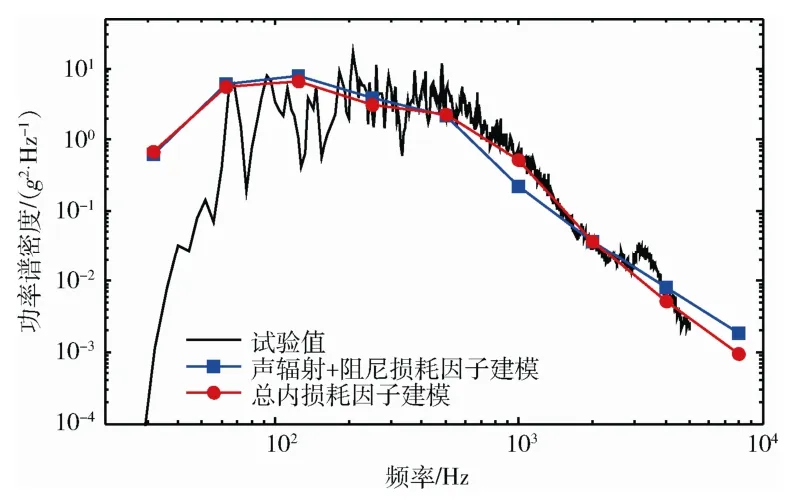
图11 声辐射损耗因子建模时太阳电池阵声振响应 计算结果与试验结果对比 Fig.11 Comparison of analysis result with radiation loss factor and test result for solar array vibro-acoustic response
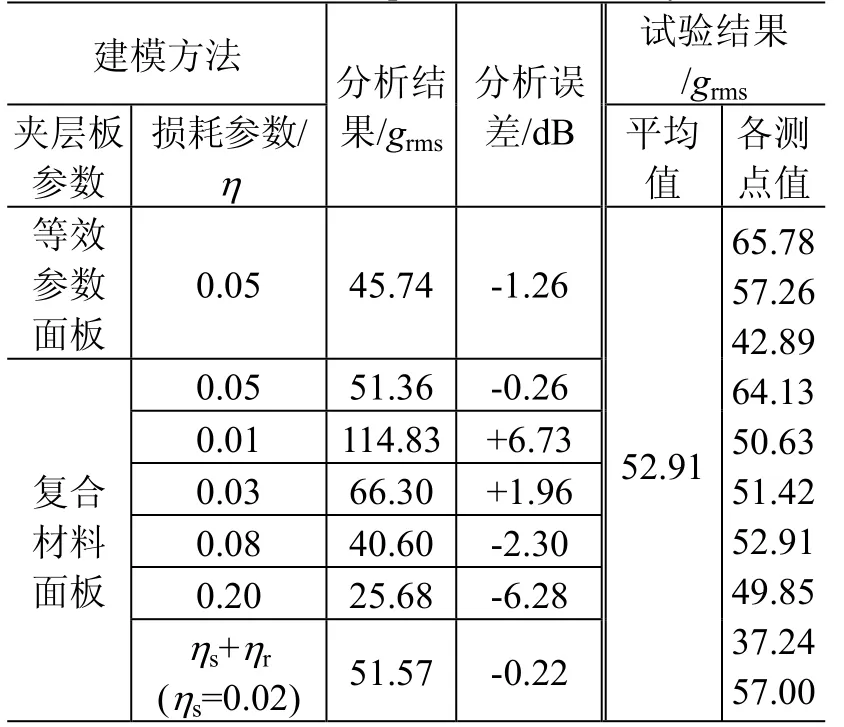
表2 太阳电池阵声振响应计算结果与试验结果总方均根 值对比 Table2 RMS comparison of analytical and test results for vibro-acoustic response of solar array
根据表2数据对比可以看出
1)取相同损耗因子参数时,采用复合材料面板建模相比采用等效参数面板建模得到的响应与试验平均结果更为吻合,前者比后者总方均根误差小1 dB。因此,太阳电池阵面板的建模方法直接关系到声场载荷输入功率的正确估算,并对声振响应分析结果影响显著。
2)子系统损耗因子的取值对声振耦合分析结果影响较大,选择合适的内损耗因子值非常重要。根据表2复合材料面板建模时η=0.05 和η=0.08 两个工况数据可知,内损耗因子60%的偏差会增加声振响应预示总方均根值偏差2 dB。
3)结合图11对比结果,太阳电池阵采用复合材料面板建模方法,取总内损耗因子0.05 时,分析结果与试验测量平均功率谱密度曲线在高频段更为吻合,总方均根误差为-0.26 dB;若考虑太阳 电池阵的声辐射损耗,结构阻尼损耗因子取0.02 时即可取得与试验结果相吻合的结果,总方均根误差为-0.22 dB。可见,两种损耗因子建模方法在总方均根分析误差上相差不大。总体上讲,基于SEA 理论的太阳电池阵声振响应分析结果与试验结果的平均值比较一致,而且随着频率增加,两者吻合性越好。虽然在低频范围内分析结果与实际测量结果存在一定差异,但是结构板声振响应的加速度总方均根分析误差可达到±0.5dB 以内,完全可满足工程需求。
4 结束语
本文开展了小卫星太阳电池阵结构的统计能量分析建模和声振响应分析,并利用太阳电池阵噪声试验结果对仿真分析进行了对比验证。对比结果表明,利用统计能量分析方法可以有效预示太阳电池阵结构的声振响应,但是模态密度和损耗因子参数的正确估计非常重要。其中,模态密度计算时需考虑太阳电池阵面板的复合材料特性及高频段夹层板的横向剪切变形影响;内损耗因子参数建议采用总内损耗因子建模时取0.05,而采用声辐射损耗模型加结构阻尼损耗因子建模时取0.02。本文声振分析的经验可为后续类似太阳电池阵结构的动力学分析和工程研制提供参考。
本文声振响应分析时,仅考虑了太阳电池阵的弯曲振动模态,对于面内剪切和拉伸模态可进一步采用有限元(FE)建模,建立混合FE/SEA 模型进行计算。在建立SEA 子系统时,确定有效质量时也仅考虑了基板和板上均布电路以及固接刚性附件的质量,忽略了伸杆、支撑梁等部件的质量。实际上,对于与基板连接的柔性部件,既不能完全忽略其质量,也不能刚性处理。因此,可以通过建立混合FE/SEA 模型进一步提高分析结果的准确性。另外,由于在低频区太阳电池阵结构模态不够密集,不能有效满足SEA 理论统计假设,因此可进一步考虑利用有限元/边界元方法进行太阳电池阵低频段声振响应分析。
(References)
[1] 姚德源,王其政.统计能量分原理及其应用[M].北京: 北京理工大学出版社,1995: 1-8
[2] Vlahopoulos N,Schiller N,Lee S.Energy finite element analysis developments for vibration analysis of composite aircraft structures[J].SAE International Journal of Aerospace,2011,4(2): 593-601
[3] Vergote K,Van Genechten B,Vandepitte D,et al.On the analysis of vibro-acoustic systems in the mid-frequency range using a hybrid deterministic-statistical approach[J].Computers and Structures,2011,89(11/12): 868-877
[4] 马兴瑞,于登云,韩增尧,等.星箭力学环境分析与试验技术研究进展[J].宇航学报,2006,27(3): 323-331 Ma Xingrui,Yu Dengyun,Han Zengyao,et al.Research evolution on the satellite-rocket mechanical environment analysis &test technology[J].Journal of Astronautics,2006,27(3): 323-331
[5] 邹元杰,韩增尧,张瑾.航天器全频域力学环境预示技术研究进展[J].力学进展,2012,42(4): 445-454 Zou Yuanjie,Han Zengyao,Zhang Jin.Research progress on full-frequency prediction techniques of spacecraft’s mechanical environment[J].Advances in Mechanics,2012,42(4): 445-454
[6] 韩增尧,曲广吉.航天器宽带随机振动响应分析[J].强度与环境,2002,29(2): 32-37 Han Zengyao,Qu Guangji.Study of wide-band random vibration response prediction for the spacecraft structures[J].Structure &Environment Engineering,2002,29(2): 32-37
[7] Lyon R H,Dejong R G.Theory and application of statistical energy analysis[M].2ndedition.Butterworth- Heinemann,1995: 49-80
[8] Renji K.Experimental modal density of honeycomb sandwich panels at high frequencies[J].Journal of Sound and Vibration,2000,237(1): 67-79
[9] Renji K,Nair P S.Modal density of composite honeycomb sandwich panels[J].Journal of Sound and Vibration,1996,195(5): 687-699
[10] 赵家宣,孔宪仁,王舒楠,等.铝蜂窝夹层板模态密度参数实验辨识[J].哈尔滨工业大学学报,2007,39(5): 807-810 Zhao Jiaxuan,Kong Xianren,Wang Shunan,et al.Experimental identification of modal density parameters of aluminum honeycomb sandwich panel[J].Journal of Harbin Institute of Technology,2007,39(5): 807-810
[11] 何蕊.基于频域小波变换的阻尼识别方法研究[D].哈尔滨: 哈尔滨工业大学,2004
[12] Renji K,Shankar N S.Loss factors of composite honeycomb sandwich panels[J].Journal of Sound and Vibration,2002,250(4): 745-761

