水下爆炸冲击作用下混凝土闸坝的失效模式分析

朱祖国，王高辉，许 昌，萧燕子

(1.长江水利委员会长江勘测规划设计研究院，湖北 武汉430010;2.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉430072;3.黄河勘测规划设计有限公司，河南 郑州450003)

混凝土闸坝由于在防洪、发电、灌溉、航运等综合利用水资源方面可以发挥重要的作用，目前国内各大流域均建有大量的闸坝。闸坝众多是淮河流域的一大特点，截止2000年淮河流域修建的闸坝已达到1.1万余座[1]。除工程本身属于混凝土闸坝外，在兴建的大型水库中，重大水工建筑物均含有闸坝结构物，如混凝土重力坝、拱坝坝身兼有溢流和泄洪作用，土石坝或堆石坝也将在岸边布置泄洪闸或陡槽式溢洪道等工程，混凝土闸坝在水利枢纽中发挥巨大的作用;然而目前在设计混凝土闸坝时主要考虑自重、静水压力、扬压力、地震荷载、共振等常规荷载，在突发爆炸荷载作用下，混凝土闸坝结构的安全性将面临严重的威胁。因此，开展水下爆炸荷载作用下的混凝土闸坝失效模式分析，对提高结构的抗爆安全性能具有重要的作用。

水下爆炸冲击作用下的结构失效是一个十分复杂的过程，然而随着计算机技术的发展，数值方法已成为研究结构抗爆性能的一种重要手段。如徐俊祥等[2]研究了水下爆炸冲击荷载作用下坝体的加速度响应及位移时程变化特点;Yu[3]采用ALE方法研究了混凝土重力坝水下接触爆炸条件下的损伤破坏特征;张启灵等[4－5]对高水位运行下混凝土坝水下爆炸冲击损伤发展及破坏模式进行了研究;张社荣等[6－8]研究了混凝土重力坝在不同爆炸方式下的可能破坏模式及抗爆性能，并重点研究了水中爆炸冲击荷载下大坝动态响应、失效模式及抗爆性能，;Wang等[9]对水下爆炸荷载下混凝土重力坝的损伤预测模型进行研究，研究了大坝上游水位及大坝高度对混凝土重力坝抗爆性能的影响[10];陆路等[11]对水下爆炸引起的混凝土坝危险性进行了估计。上述研究成果主要集中在混凝土重力坝，然而针对混凝土闸坝在水下爆炸荷载作用下的失效模式分析较少，有待进一步研究。

文中通过建立混凝土闸坝厂房坝段水下爆炸全耦合模型，基于显示动力程序LS－DYNA对水下爆炸冲击荷载作用下闸坝厂房坝段的失效破坏过程进行分析，研究炸药在闸坝进口段内部和库前水下爆炸对闸坝抗爆安全性能的影响。

1 高应变率下的混凝土动态损伤本构模型

混凝土是一种率相关的脆性材料，在爆炸高加载率下应变率高达 10/s～103/s[12]，其强度将显著提高。Holmquist等[13]在 Johnson－Cook模型的基础上提出了可考虑爆炸冲击荷载作用下混凝土的大变形、高应变率及高压下产生的损伤、破碎和断裂等问题的混凝土动力损伤本构模型(Holmquist Johnson Cook，HJC)，该模型如图1所示。

图1 高应变率下的混凝土本构模型

图1(a)为HJC模型的等效强度模型，可表述为:

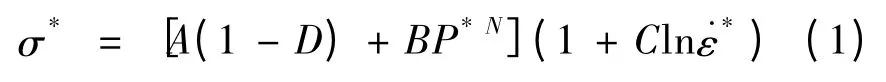
式中，σ*是标准化等效应力;σ是实际等效应力是静态抗压强度;P*=是标准化静水压力;P是实际静水压力是无量纲应变率;˙ε是实际应变率是参考应变率;D(0≤D≤1)为损伤度;A、B、N、C为材料的强度参数。

图1(b)为混凝土材料的损伤累积破坏模型，可以表示为:

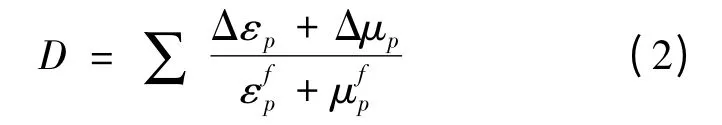
式中:Δεp为等效塑性应变增量;Δμp为塑性体积应变增量为等效塑性应变为塑性体积应变;为总塑性应变，其表达式为=D1(P*+T*)D2式中，T为最大拉伸强度;D1和D2为损伤常数，T*为标准化最大拉伸强度。损伤常数Efmin=0.01为最小塑性应变，且 D1(P*+T*)D2≥Efmin。

图1(c)为 HJC模型的状态方程，主要包括:(1)线弹性阶段(OA)，满足K=Pcrush/μcrush(Pcrush为压垮的静水压力;μcrush为压垮的体积应变，K为体积弹性模量);(2)过渡阶段(AB);(3)完全密实阶段(BC)，满足，式 中，¯μ =(μ - μlock)/(1+ μlock)，K1、K2、K3为材料常数。

混凝土动态损伤本构模型(亦即 HJC本构模型)中相关参数[13]见表 1。

表1 HJC本构模型的相关参数[13]

2 库前水下爆炸冲击荷载下混凝土闸坝抗爆性能分析

2.1 数值模型

国内某工程枢纽由左、右岸挡水坝段、河床式厂房坝段、泄洪闸坝段等建筑物组成。上游正常蓄水位1 015.00 m，下游水位 986.92 m，坝顶长度 461.13 m，最大坝高72.8 m，混凝土闸坝厂房坝段的几何示意图如图2所示。当炸药在库前水下爆炸后，产生的爆炸冲击荷载将直接作用于厂房坝段的进口段，且爆炸冲击荷载峰值衰减较快，结构破坏往往在短时间内发生，水下爆炸能量主要对进口段造成破坏，进口段后部发电厂房结构受冲击波荷载的直接作用强度较小。因此，本次主要取厂房坝段的进口段为研究对象，暂不考虑发电厂房的破坏，计算区域如图2所示。

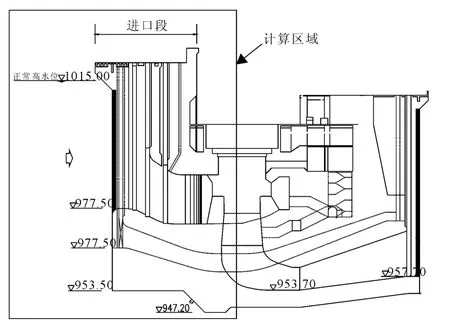
图2 混凝土闸坝厂房坝段剖面

为了研究水下爆炸冲击波对大坝破坏的影响规律，模拟采用了集中装药一次引爆模式的简化模型，主要包括:采用Euler网格模拟高能炸药、库水、空气;采用Lagrange网格模拟大坝结构;大坝与库水之间的交界面采用Lagrangian－Eulerian流固耦合算法[14]。根据图2所示的计算区域，建立有限元计算模型如图3所示，单元总数为428 544个，节点总数为456 100个，炸药、库水、空气的材料模型及状态方程参考文献[15]。假定高能炸药位于水下深度10 m，分别计算炸药位于进口段内部和位于坝前10 m处两种工况，炸药用量为1 000 kg。为了研究水下爆炸冲击荷载作用下混凝土闸坝的失效过程，考虑了混凝土断裂失效(拉伸应变值大于0.002)。在模型截断边界处施加无反射边界条件;进口段与厂房交接处采用法向约束，坝基底部施加全约束。

图3 厂房坝段进口段水下爆炸全耦合模型

2.2 炸药在进口段库前爆炸

当炸药在库前水下爆炸时，大坝的破坏模式如图4所示。由图4可知，当高能炸药的用量为1 000 kg时，在库前水下爆炸冲击荷载作用下，首先在中墩上游面坝头与直立面交接处产生开裂破坏;随着冲击波的传播，该裂缝贯穿至中墩与胸墙交接处;在进口段与厂房顶部交接处，由于厂房顶部提供支点，中墩、边墩以及胸墙均在该高程贯穿贯穿性裂缝，主要为脆性开裂破坏;同时在闸墩与进口段底板交接处，由于受到冲击荷载作用，产生较大的剪切作用，在此处也产生剪切开裂破坏，且中墩的裂缝贯穿至流道顶板处。

2.3 炸药在进口段内部爆炸

当高能炸药在进口段内部水域发生爆炸时，大坝的失效模式如图5所示。由图5可知，当高能炸药的用量为1 000 kg时，在进口段内部水下爆炸冲击荷载作用下，进口段中墩由于离爆源较近，闸墩被压垮震碎;随着爆轰能量的传播，由于中墩吸收了较大部分能量，侧墩主要产生脆性破坏，在离爆源下部高程10 m左右处产生了贯穿上下游的开裂破坏;同时在胸墙与厂房交接处由于应力集中，也出现了贯 穿性裂缝。

图4 库前水下爆炸冲击荷载作用下的混凝土闸坝失效模式

由以上分析可知，当炸药在库前水下浅水近场爆炸时，进口段闸墩主要表现为脆性开裂破坏和剪切破坏，主要在中墩坝头与上游直立面交接处产生贯穿至胸墙处的裂缝，并在厂房顶部高程处，中墩、边墩及胸墙产生贯穿性裂缝，同时在闸墩与进口段底板交接处也出现剪切开裂破坏;当炸药在进口段内部爆炸时，中墩将被震碎，且边墩和胸墙均产生贯穿性裂缝。

3 结论

本文通过建立混凝土闸坝厂房坝段全耦合水下爆炸模型，分析了水下爆炸作用下闸坝进口段的失效模式。主要得到以下结论:

(1)水下爆炸荷载由于其短持时、强峰值特性，对混凝土闸坝结构的安全构成严重的威胁，在结构设计运行时应给以关注;

(2)混凝土闸坝在水下爆炸冲击荷载作用下将发生严重的破坏，当炸药在库前水下浅水近场爆炸时，进口段闸墩主要表现为脆性开裂破坏和剪切破坏;(3)当炸药在进口段内部爆炸时，中墩将被震碎，边墩和胸墙均产生贯穿性裂缝，且比库前水下爆炸破坏更加严重。

[1]夏 军，赵长森，刘 敏，等.淮河闸坝对河流生态影响评价研究——以蚌埠闸为例[J].自然资源学报，2008，23(1):48-60.

[2]徐俊祥，刘西拉.水中爆炸冲击下混凝土坝动力响应的全耦合分析[J].上海交通大学学报，2008，42(6):1001-1004.

[3]Yu T. Dynamical response simulation of concrete dam subjected to underwater contact explosion load[C]//2009 WRI World Congress on Computer Science and Information Engineering，2009.

[4]张启灵，李端有，李 波.水下爆炸冲击作用下重力坝的损伤发展及破坏模式[J].爆炸与冲击，2012，32(6):609-615.

[5]张启灵，李 波.高水位运行下近水面水下爆炸对拱坝结构的影响[J].应用力学学报，2013，30(2):153-159.

[6]张社荣，王高辉.混凝土重力坝抗爆性能及抗爆措施研究[J].水利学报，2012，43(10):1202-1213.

[7]张社荣，王高辉.水下爆炸冲击荷载下混凝土重力坝的抗爆性能[J].爆炸与冲击，2013，33(3):255-262.

[8]张社荣，王高辉，王 超，等.水下爆炸冲击荷载作用下混凝土重力坝的破坏模式[J].爆炸与冲击，2012，32(5):501-507.

[9]Wang G，Zhang S. Damage prediction of concrete gravity dams subjected to underwater explosion shock loading[J]. Engineering Failure Analysis，2014，39:72-91.

[10]Zhang S，Wang G，Wang C，et al. Numerical simulation of failure modes of concrete gravity dams subjected to underwater explosion[J]. Engineering Failure Analysis，2014，36:49-64.

[11]陆 路，李 昕，周 晶.水下爆炸引起的混凝土坝危险性估计[J].水资源与水工程学报，2010(5):6-9.

[12]Malvar L J，Ross C A. Review of strain rate effects for concrete in tension[J]. ACI Materials Journal，1998，95(6):735-739.

[13]Holomquist T J，Johnson G R，Cook W H. A computational constitutive model for concrete subjective to large strains，high strain rates，and high pressures[C]//Jackson N，Dickert S. The 14th International Symposium on Ballistics，USA:American Defense Prepareness Association，1993.

[14]张社荣，孔 源，王高辉.水下和空中爆炸时混凝土重力坝动态响应对比分析[J].振动与冲击，2014(17):47-54.

[15]张社荣，孔 源，王高辉.水下和空中爆炸冲击波传播特性对比分析[J].振动与冲击，2014，33(13):148-153.