地下洞室超挖预测的费歇判别分析方法
邓 宇
(成都四海岩土工程有限公司,四川 成都610093)
在公路、铁路、水利、地下储库等地下洞室的开挖施工过程中,超挖现象经常出现,是一个很普遍的问题。尤其是对于跨度较大的大断面隧道,在地质条件不太好的情况下,超挖现象更加普遍。另外一方面,虽然当前隧道开挖数量和规模越来越大,但仍然普遍采用钻爆法进行施工,TBM或盾构法无法全面替代钻爆法。利用钻爆法进行施工时,如果遇到岩体种类繁多,地质条件比较复杂的情况,在一般开挖技术施工情况下,超挖现象非常容易出现。
本质上,超挖现象主要是由于岩体内部的结构面和开挖形成的临空面进行组合而产生的。开挖过程中形成临空面,如果关键块体的优势面抗剪强度比下滑力小时,关键块体会自动滑落,从而对原有的断面形成超挖[1-2]。为了防止超挖现象的产生,非常有必要对位于洞室开挖面范围外的不稳定块体的超挖进行预测,从而利用预测结果指导洞室的开挖施工、并能够改善岩体结构的受力状况,避免因为超挖造成不必要支护进而降低工程造价。目前对超挖预测的研究也有很多。例如岩体稳定性理论、光爆参数控制方法等[3-4];苏永华等对3条隧道现场测量了360个断面的最大超挖现象的样本数据,并根据所在断面围岩的类别,详细研究了超挖样本数据的统计特征,认为Ⅲ类、Ⅳ类、Ⅴ类岩体中隧道围岩的最大超挖数值可以用分形来描述[5]。魏继红等基于结构面网络模拟理论及块体理论,根据分析中的结构面特征参数值,预测了某座连拱隧道的超挖[3];孙少锐等则将地质统计模型、小波神经网络、超挖预测这三种基本理论进行了有机的结合,并利用该方法研究了地下洞室超挖预测的问题[4];吴继敏等基于力学机理分析,提出了一种网络模拟技术,并利用该技术对地下洞室的超挖预测进行了研究[6]。本文借鉴了费歇判别分析理论的思想,建立了隧道超挖预测的费歇(Fisher)判别分析模型,利用该模型在实际工程中进行了运用,研究效果良好。
1 费歇判别分析理论
1.1 费歇判别分析方法
费歇(Fisher)判别思想是历史上最早提出的判别方法之一,其基本思想是对多维问题进行简化,成为一维问题进而处理[7]。选择适当的投影轴,对所有的样品点在这个轴上进行投影,分别得到一个对应的投影值,使得类与类之间尽可能分开。在选择投影轴时,提出的要求是:使得每一类的投影值所形成的类内离差尽可能小,而尽量使不同类间的投影值所形成的类间离差较大。
设有m个总体G1,G2,…,Gm,分别对应的均值向量和协方差矩阵u(1),u(2),…,u(m);V(1),V(2),…,V(m)。在总体Gi中进行抽样,并且抽取容量是ni的样本数据:
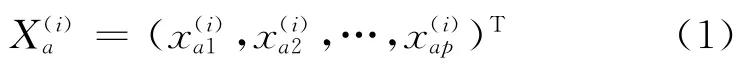
则:
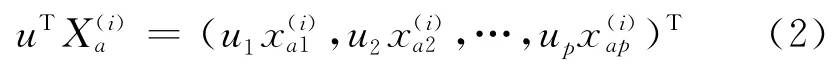
为在轴上的投影。其中:a=1,2,…,ni;i=1,2,…,m;向量u= (u1,u2,…,up)T,表示为p维空间的某1个方向;Y=uTX,表示u与X的内积,即X在u轴上的投影为:

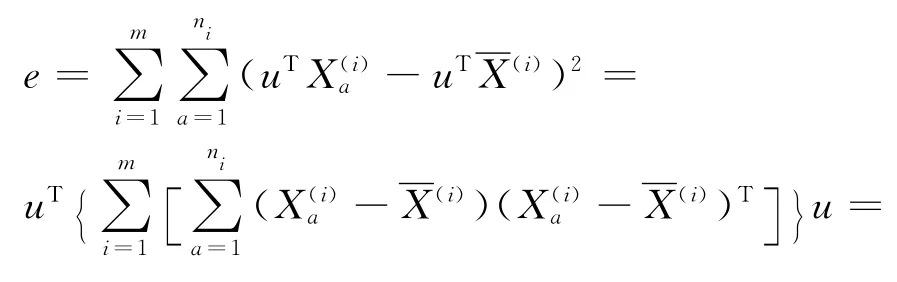

上式中Si是Gi中ni个样本X(i)a(a=1,2,…,ni)的样本离差阵,则组间差为:

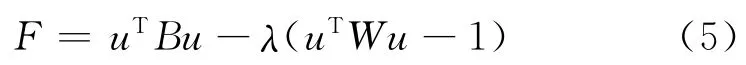
对上式求偏微分,并使之为0。即:
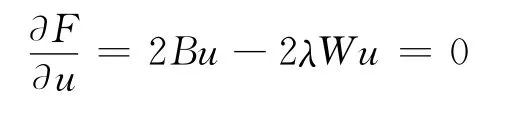
经进一步整理得:
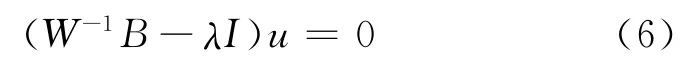
从上可知λ应是W-1B的最大特征值,u为最大特征值λ相对应的特征向量,从而求出判别函数。
1.2 判别准则的评价
获得上述判别准则后,必须对判别准则的优良性进行考察,本文中主要采用交叉确认估计法进行误判率的计算。
假设存在两个总体,分别用G1和G2表示,并且两个总体容量分别用n1和n2表示。对误判率进行交叉确认估计时,通常是每次剔除训练样本其中一个样品,对剩余的容量n1+n2-1的样本进行处理,并建立相应的判别准则,进而用建立的判别准则对删除的那个样品进行判别,并以所得到误判的比例值作为误判概率的估计值。进行计算时的具体步骤可以表示如下:
(1)对总体G1的训练样本,从其中剔除某一个样品,对剩余的n1+n2-1的训练样本,建立一个相应的判别函数;
(2)利用建立的判别函数,对第(1)步中被剔除的样本,判别其总体属性;
(3)对步骤(1)、(2)进行重复,一直到总体G1中的所有的训练样本被全部剔除,并且计算误判的样品个数,记为;
(4)对总体G2的训练样本,也进行步骤(1)~步骤(3)的重复,并计算误判样品个数,记为n*21;
(5)最后利用下式来计算最终的误判率η:
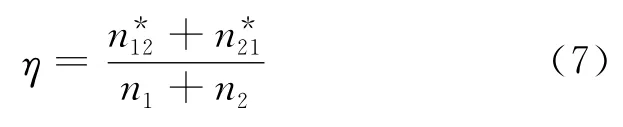
2 隧道超挖预测的费歇判别分析法
2.1 隧道超挖预测的参数确定
造成地下洞室超挖的因素有很多,其中自然因素占很大影响,围岩地质构造、结构面切割、节理发育情况直接影响隧洞的超挖。因此,对地下洞室的超挖预测研究,必须对围岩的几何特征(产状、延伸和间距)作详细调查,并在调查的基础上,确定超挖体积的范围,进而对超挖情况做出合理预测。
由于工程地质条件的复杂多样,在对围岩进行调查时,应该根据工程实际情况选出相应的几何参数。为了说明费歇判别分析方法的具体应用,本文采用文献[4]的工程实例资料进行说明。选取5个参数作为影响隧洞超挖的几何影响因素,即:2组节理、层面、延伸、间距。进而采用8个具体参数作为隧洞超挖费歇判别分析模型的输入参数(见表1)。

表1 费歇判别分析法中的训练样本
将超挖块体的体积大小分成4个种类,即4个总体:(1)V>2.4m3,模型输出为G1;(2)V=2.4 m3~2.1m3,模型输出为G2;(3)V=2.1m3~1.8 m3,模型输出为G3;(4)V<1.8m3,模型输出为G4。该分类标准对于不同的工程,可根据需要修改体积范围。
2.2 费歇判别分析模型实例应用
某市西南郊10km处存在一处抽水蓄能电站工程。根据该工程对不同工程结构面进行实测的资料,从中选择了21个样本作为费歇判别分析模型的学习样本(见表1)。经过学习后,模型的实际输出与期望输出一致,利用交叉确认估计法,得到该模型的误判率为0,说明训练结果较好,模型判别能力稳定。
为了检验该模型的实际判别能力,选用该工程中平洞4的实例资料进行验证。由表2可知,平洞4的预测结果为G1,说明超挖体积比较大。与之形成对比的是,对该工程进行实际调查时,也发现平洞4的岩层倾角相对比较大,并且与两组节理面组合形成比较大的切割块体,说明本文中给出的预测结果相对比较符合实际的情况,并且和神经网络法一致[4]。
3 结 语
(1)提出了地下洞室超挖预测的费歇判别分析方法。考虑影响超挖的围岩几何参数,并结合工程实例给出了费歇判别分析方法应用于隧洞超挖预测的计算过程,进而对建立的模型利用交叉确认估计法进行了误判率的估计。该方法充分考虑了人们在研究地下洞室超挖过程中的先验信息,并在抽取样本的过程中进行修正,判别能力相对较强,为预测地下洞室的超挖提供了一条新的思路和途径。
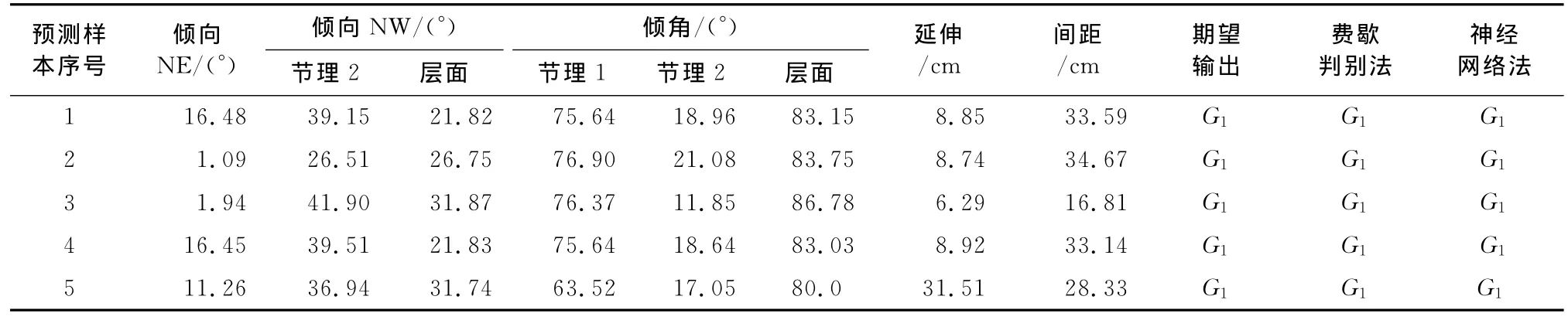
表2 费歇判别分析法所得到的预测结果表
(2)费歇判别分析方法首次运用到地下洞室的超挖预测研究中,仍然存在一些问题有待深入研究。例如影响隧洞超挖的主要因素主要有些,本文给出的选择是否一定合理?判别模型中的判别因子怎样选取等等。在今后的研究工作中,可以考虑搜集更多的工程实例数据,建立相应的数据库,加强隧洞超挖预测费歇判别分析模型的训练,并使得该模型更加完善,进而使预测结果更加接近实际情况。
[1]Chakraborty A K,Raina A K,Ramulu M,et al.Development of rational models for tunnel blast prediction based on a parametric study[J].Geotechnical and Geological Engineering,2004,22(4):477-496.
[2]Maerz N H,Ibarra J A,Franklin J A.Overbreak and underbreak in underground openings part 1:measurement using the light section method and digital image processing[J].Geotechnical and Geological Engineering,1996,14(4):307-323.
[3]魏继红,孙少锐,彭建忠,等.高速公路连拱隧道超挖预测及评价研究[J].岩石力学与工程学报,2006,25(S1):3324-3329.
[4]孙少锐,吴继敏,魏继红.基于地质统计模型的小波神经网络在地下隧洞超挖预测中的应用[J].岩石力学与工程学报,2003,22(8):1344-1349.
[5]苏永华,孙晓明,赵明华.隧道围岩超挖的分形特征研究[J].中国矿业大学学报,2006,35(1):89-93.
[6]吴继敏,孙少锐,魏继红.应用力学机制的网络模拟预测洞室超挖问题[J].岩土力学,2004,25(8):1220-1224.
[7]王学民.应用多元分析[M].上海:上海财经大学出版社,1999.

