盾构隧道近距离平行穿越原水管道沉降分析

王培利 雷震宇 周 骏

盾构隧道近距离平行穿越原水管道沉降分析

王培利 雷震宇 周 骏

地铁盾构推进过程中会对隧道周围建（构）筑物和土层造成不同程度的影响。文章以上海轨道交通8号线某区间盾构隧道穿越既有原水管道为工程背景，应用ABAQUS有限元三维数值方法，分析盾构穿越既有原水管道时的原水管道沉降变形特征，分析不同施工参数对原水管道沉降的影响，并对既有原水管道沉降变形进行现场监测分析。计算和实测结果均表明原水管道沉降满足《上海市原水引水管渠保护办法》的规定要求。

盾构隧道；下穿原水管道；管线沉降

盾构隧道施工打破了地下管线周围土体原有的力学平衡，带动邻近地下管线一同移动，致使管线产生一定程度的附加变形与附加应力。文献[1]详细叙述了盾构法隧道的施工过程、反应施工质量的等代层模拟方法，文献[2]给出了在盾构开挖前地应力的平衡过程。文献[5]采用数值计算方法，按管隧垂直、管隧平行2种情形，较为详细地分析了土质、管线的直径、壁厚、截面形状、材质、管隧垂直间距、管隧水平间距等因素对地下管线的影响规律。本文采用三维有限元方法，建立符合实际工程特征的三维模型，模拟盾构推进的各种工况及施工因素（包括成层土、注浆等）的相互作用，分析上海轨道交通8号线某区间盾构穿越既有原水管道时对原水管道沉降的影响。

1 工程概况

上海轨道交通8号线某区间盾构隧道穿越既有Φ1.8 m原水管道，主要影响里程为XK30+735～XK30+935。隧道主要穿越的土层为灰色淤泥质粘土层，该层土呈流塑状态，强度低、压缩性高、渗透性弱、分布均匀，是上海地区盾构推进较为有利的土层（图1）。主要土层土力学性质见表1。

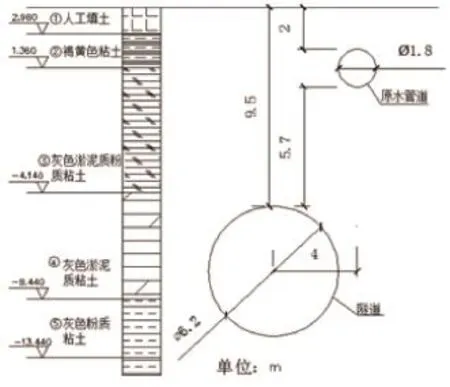
图1 原水管道与下行线盾构隧道位置关系

2 有限元模拟分析

2.1 模型建立

首先，用ABAQUS/CAE建立土体、原水管道和衬砌、等代层模型，X为宽度方向，Y为深度方向，Z向为盾构掘进方向。本文选取三维有限元土体模型为200 m×60 m×30 m（依次为盾构掘进方向Z、宽度X和深度Y）。取土体本构模型为线性Drucker-Prager模型，混凝土衬砌和钢管为弹性材料。衬砌管片为C55、S10钢筋混凝土，尺寸为外径6.2 m，厚度0.35 m，长度1.2 m；原水管道尺寸为外径1.8 m，厚度0.1 m（图2）。

表1 主要土层土力学性质表

图2 三维有限元模型图

2.2 模型参数选取

在影响围岩稳定性的各因素中，土体及衬砌材料的力学性质可通过试验测定，难以确定的是盾尾空隙、土体向盾尾空隙的自然填充及注浆后浆体的分布情况和隧道壁面受扰动的程度和范围。在实际施工中，要对它们分别进行量化是难以达到的，为此，将它们概化为一匀质、等厚、弹性的等代层，等代层的厚度δ可取为：

式（1）中， Δ为盾尾空隙的理论值，包括超开挖间隙、盾构壳厚度对应间隙以及操作间隙；η为折减系数，取值范围为0.7～2.0，对于硬土层取下限，对极软的土层取上限。上海地区为极软土层，η取2.0。

表2 盾构推进模拟参数表

表2给出了钢管道、混凝土、等代层等盾构推进模拟参数。

2.3 地应力平衡

在模拟基坑开挖、隧道开挖、工后沉降、桩土复合地基、挡土墙等工程问题中，都需要平衡初始地应力，以最终得到既满足平衡条件又不违背屈服准则的初始应力场，并保证各节点的初始位移近似为0。

2.4 盾构掘进模拟

盾构掘进过程模拟如下：

（1）在地应力平衡后，把原水管道实体解除锁死，恢复原始的模型状态；

（2）在盾构机开始掘进之前，盾构机对开挖面土体有顶推力F(面荷载)，顶推力F按式（2）计算：

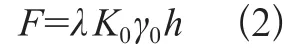
式（2）中， γ0为被移除土体重度 ( 本例取1 980 kN/ m3）；h为土体深度 ( 本例为8.86～15.34 m)；K0为土体侧压力系数 ( 本例取0.22)；λ为扰动系数 ( 根据计算情况调整而定）；

（3）在此分析步骤中，移除第1个开挖土体单元（长2 m），并相应激活等长度的等代层和衬砌；

（4）由于盾构机掘进对前方土体的扰动，分析步骤中相应衰减下一个即将被移除土体的弹性模量，即，将被移除的土体弹性模量衰减30%；

（5）按前4步的步骤如此循环，直至200 m长的土体被全部开挖，并完成隧道支护。

2.5 模拟结果分析

本次模拟盾构隧道平行穿越原水管道1次掘进2 m，并激活相应的衬砌和等代层（注浆层）。Z向为盾构掘进方向和原水管道纵向，Y向为垂直位移方向，正值为隆起，负值为沉降，并设定初始开挖面为Z=0 m，终止开挖面为Z=200 m。

2.5.1 原水管道纵向沉降分析

为揭示不同掘进程度对原水管道纵向沉降的影响，同时考虑规避模型边界约束的影响，模拟计算中选取开挖面位置为Z=30、60、90、120、150、180 m时的原水管道纵向沉降，计算结果分别见图3～8，由图3～8可见：

（1）当盾构隧道掘进到Z=30 m时，原水管道在Z=0 m处的沉降为1.44 mm，并沿着盾构掘进方向逐渐增大，在Z=15 m处达到最大，为1.55 mm，然后沉降逐渐减小，直至距离开挖面后30 m处（即Z=60 m）之后，沉降接近0（图3）；

（2）当盾构隧道掘进到Z=60 m时，原水管道在Z=0 m处的沉降为1.44 mm，并沿着盾构掘进方向逐渐增大，在Z=40 m处达到最大，为2.39 mm，然后沉降逐渐减小，直至距离开挖面后30 m处（即Z=90 m）之后，沉降接近0（图4）；

图3 开挖面Z=30 m时原水管道管沉降曲线

图4 开挖面位置Z=60 m时原水管道管沉降曲线

（3）当盾构隧道掘进到Z=90 m时，原水管道在Z=0 m处的沉降为1.63 mm，并沿着盾构掘进方向逐渐增大，并在Z=60 m处达到最大，为2.57 mm，然后沉降逐渐减小，直至距离开挖面后30 m处（即Z=120 m）之后，垂直位移接近0（图5）；

图5 开挖面位置Z=90 m时原水管道管沉降曲线

（4）当盾构隧道掘进到Z=120 m时，原水管道在Z=0 m处的沉降为1.75 mm，并沿着盾构掘进方向逐渐增大，在Z=50 m处达到最大，为2.6 mm，在Z=50 m至Z=95 m这一段沉降几乎保持不变，然后沉降逐渐减小，直至距离开挖面后30 m处（即Z=150 m）之后，沉降接近0（图6）；

图6 开挖面位置Z=120 m时原水管道管沉降曲线

（5）当盾构隧道掘进到Z=150 m时，原水管道在Z=0 m处的沉降为1.81 mm，并沿着盾构掘进方向逐渐增大，在Z=50 m处达到最大，为2.7 mm，在Z=50 m至Z=135 m这一段沉降几乎保持不变，然后沉降逐渐减小，直至距离开挖面后30 m处（即Z=180 m）之后，沉降接近0（图7）；

（6）当盾构隧道掘进到Z=180 m时，原水管道在Z=0 m处的沉降为1.86 mm，并沿着盾构掘进方向逐渐增大，在Z=50 m处达到最大，为2.78 mm，在Z=50 m至Z=160 m这一段沉降几乎保持不变，然后沉降逐渐减小，直至Z=200 m处沉降为0.8 mm（图8）。

2.5.2 不同注浆量对沉降的影响

为计算分析施工中不同注浆量对原水管道沉降的影响，模拟计算中施工过程中，合适的注浆量按3.7 m3/环计算，不足注浆量按3 m3/环计算，在计算上以减小等代层模量（0.1倍）的方法来模拟。

图9给出了开挖面位置Z=200 m时不同注浆量对原水管道沉降的影响曲线，由图9可以看出，不同注浆量对原水管道沉降量影响较大，注浆量为3.7 m3/环时的原水管道沉降量较注浆量为3 m3/环时的原水管道沉降量降低约3.5 mm。可见，在盾构掘进过程中采取同步注浆和二次注浆的方法，可有效减少原水管道沉降量。

3 施工监测

3.1 监测点布置

根据现场实际情况，本监测在原水管道之上布置测点，以观测原水管道沉降变化。考虑施工和原水管的安全，在施工段两侧的原水管道各延伸20 m进行布点。由于在盾构掘进到下行线390～430环与480～520环（共96 m），对原水管道影响较大，故对该区段进行重点监测，适当增加测点数，该区段的测点按6 m间距布设，其余段按12 m间距布设，测点总数为40个。具体布点情况参见图10。

图7 开挖面位置Z=150 m时原水管道管沉降曲线

图8 开挖面位置Z=180 m时原水管道管沉降曲线

图9 不同注浆量对原水管道沉降的影响

图10 监测点布置

3.2 监测结果

在整个实际开挖过程中时，根据现场监测点的布点位置，选取盾构开挖面至Z=148 m和Z=188 m位置处时，测量原水管道沿纵向的实测沉降变化规律，见图11、12。由图11、12可见：

（1）当盾构掘进到Z=148 m时，原水管道在Z=0 m处的实测沉降值为1.35 mm，并沿着盾构掘进方向沉降在1～2 mm间变化，至原水管道Z=100 m后沉降逐渐增大，并在原水管道Z=145 m处达到最大，为2.8 m m，之后沉降逐渐减小，直至原水管道Z=200 m处沉降接近0（图11）；

（2）当盾构掘进到Z=188 m时，原水管道在Z=0 m处为的实测沉降值约为1.2 mm，并沿着盾构掘进方向实测沉降保持在1.2～1.4 mm之间，至原水管道Z=145 m后实测沉降逐渐增大，并在原水管道Z=180 m处达到最大，实测最大沉降值约为3.1 mm，之后实测沉降逐渐减小至原水管道Z=200 m处的2.6 mm（图12）；

4 结论

《上海市原水引水管渠保护办法》规定“钢管垂直方向附加变形≤0.01D”，对于本例，原水管道直径为D=1.8 m，原水管道垂直向附加变形应≤18 mm。本文有限元模拟计算和现场实测原水管道最大沉降分别为2.78 mm和3.1 mm，模拟计算和实测结果均表明，盾构隧道穿越既有原水管道时，原水管道沉降满足《上海市原水引水管渠保护办法》的规定要求。

[1] 陈卫忠, 伍国军, 贾善坡. ABAQUS在隧道及地下工程中的应用[M].北京：中国水利水电出版社, 2010.

[2] 曹金凤, 石亦平. A BAQUS有限元分析常见问题解答[M]. 北京：机械工业出版社, 2010.

[3] 费康, 张建伟. ABAQUS在岩土工程中的应用[M]. 北京：中国水利水电出版社, 2010.

U456.3

王培利：同济大学铁道与城市轨道交通研究院，硕士研究生，上海 201804