南京马尾松根径与胸径多元混合效应模型研建

赵浩彦，张民侠 ，张 洁 ，方 彦，邵长生 ，陈戈萍

（1.南京森林警察学院，南京 江苏 210023；2.南京市老山林场，江苏 南京 211811）

南京马尾松根径与胸径多元混合效应模型研建

赵浩彦1，张民侠1，张 洁1，方 彦1，邵长生2，陈戈萍1

（1.南京森林警察学院，南京 江苏 210023；2.南京市老山林场，江苏 南京 211811）

为了建立南京地区马尾松Pinus massoniana根径与胸径的相关关系模型，基于28块20 m ×20 m的方形样地的531株马尾松根径和胸径数据，分别采用线性、乘幂、双曲线、三次曲线等11种一元模型和多元非线性混合效应模型拟合了马尾松根径和胸径的相关关系。结果表明，所有一元模型的相关指数均大于0.8，其中，一元线性模型的拟合优度最高（R2=0.919，SEE=1.854 8），总相对偏差、平均相对误差和平均相对误差绝对值最小（TRB=-1.34%，E=1.33%，P=7.734%）。适应性检验结果显示，一元线性模型有较好的适用性（E=1.125%，P=7.4645%）。与一元线性模型相比，多元非线性混合效应模型有更高的拟合优度和精度（R2=0.9504，SEE=1.7973，TRB=0.32%，E=0.313%，P=5.6428%）。模型适应性检验显示，多元非线性混合效应模型有更强的适用性（E=-0.0888%，P=5.3594%），从而表明，与一元线性模型相比，多元非线性混合效应模型能更精确地拟合马尾松根径（d0）和胸径的相关关系。

马尾松；根径；胸径；一元线形模型；多元非线性混合效应模型

马尾松是一种喜光、喜温的树种，适生于年均温为13～22 ℃，年降水量800～1 800 mm、最低温度不到-10℃的环境。它同时是中国长江流域各省重要的荒山造林树种，也是江南自然风景区普遍绿化及造林的重要树种，同时也是经济价值较高的主要用材树种。目前，关于马尾松的盗伐、滥伐案件逐渐增加，在对这些案件进行定罪量刑的过程中，如何根据其根径精确计算其材积就成为一个亟待解决的问题。

由于树木被伐，能测定的因子只有根径，故只能通过根径推算被伐木材积。通常是根据林木材积和根径的实测数据，通过拟合根径材积方程来编制一元根径材积表。很多学者已经拟合了不同地区多个树种的根径材积模型并编制了相应的根径材积表[1-5]。

但是，根径一元材积模型的预估精度要明显低于胸径一元材积模型。所以，很多学者根据拟合的树木胸径和根径回归方程，由根径推算胸径从而确定林木的材积，或者将胸径材积表导算成根径材积表。杨艳丽等[6]运用一元线性方程分别拟合了青海省大通县青海云杉、青杨和白桦3个树种根径和胸径的相关关系模型，并根据建立的模型，将3个树种的胸径材积表导算成根径材积表。经适应性检验，发现用导算出的地径材积表和用胸径材积表计算的立木材积并无显著差异。张金全[7]采用线性和双曲线方程分别拟合了福建省建瓯市马尾松、杉木和阔叶树根径和胸径的相关关系，研究发现双曲线为最佳模型，并根据建立的模型和胸径材积公式，分别编制了建瓯市马尾松、杉木和阔叶树的根径材积表。王华用[8]一元线性方程拟合了黔南地区马尾松根径和胸径的相关关系，研究发现模型拟合优度和精度较高。赵芳等[9]通过选用线性、对数、双对数、倒数等5个方程拟合了福建延平区杉木根径和胸径的相关关系，检验显示双对数方程（即乘幂方程）的拟合效果最佳，并根据双对数方程和胸径材积表导出杉木根径材积表。李宝银等[10]分别选用线性和双曲线方程拟合了福建沙县杉木、马尾松和阔叶树根径和胸径相关关系，结果显示双曲线方程的拟合效果更好，并根据双曲线方程和胸径材积表分别导出这3个树种的根径材积表。因根径材积表与胸径材积表之间并不是相互独立的，而是相互关联的，曾伟生[11]利用误差变量联立方程组方法，同时建立了南方杉木胸径材积模型、胸径-根径回归模型和根径材积模型，结果显示，与线性方程相比，双曲线方程可更好地反映根径和胸径之间的相关关系。林銮勇[12]运用一元线性和双曲线2个方程建立了福建柏根径和胸径的相关关系模型，结果显示，这两个方程拟合效果均较好。王允寿等[13]运用一元线性拟合了山东省侧柏、松类、黑杨和刺槐4个树种的根径和胸径的相关关系模型，并采用方差分析法对拟合的模型进行了显著性检验，结果显示，4 个树种地径和胸径的线性关系都达到了极显著水平。刘健等[14]采用线性、乘幂、双曲线、对数等5个方程分别拟合了福建省闽北地区杉木、马尾松和阔叶树地径和胸径的相关关系，结果显示，杉木和阔叶树以一元线性、马尾松以幂函数为最佳模型。

但是，目前建立的根径和胸径的相关关系模型的参数都是固定因子，没有考虑样地因子（林分密度、林分年龄和立地条件等）对根径和胸径之间相互关系的影响。其实，林分密度不同，林分年龄不同，立地条件不同，建立的根径和胸径相关关系模型的参数也存在差异，用传统的一元模型不能表达这种差异，而多元混合效应模型则能较好地表达这种差异。

文章正是基于以上思路，选择南京市老山林场的28块不同年龄和不同林分密度的马尾松林分作为研究对象，分别采用多种一元模型和多元非线性混合效应模型拟合马尾松林木根径和胸径的相关关系并对所建模型进行比较，从中选出拟合优度最好、精度最高的模型，从而为用马尾松胸径材积模型（表）计算倒木材积提供理论依据。

1 材料与方法

1.1 研究区概况

老山林场位于长江北岸、南京西北郊的江浦县境内，地处东经 118°25′～ 118°40′E，北纬 32°03′～32°09′。全场东西长约35 km，南北宽约15 km，至1999年统计，全场面积为7 493.33 hm2。

该区属北亚热带气候区，呈明显的季风性气候，具有夏季炎热、冬季寒冷、四季分明，雨量充沛，日照充足，无霜期较长的特征。年平均气温15.3 ℃，最高温为21.1 ℃，最低为11.3 ℃。年平均等于或高于10 ℃的生长期平均为228 d；常年平均月日照时数为197.1 h；年平均降雨量为1 000～1 050 mm；年平均无霜期为223 d；土壤类型有6大类：水稻土、黄棕壤、石灰岩土、紫色土、白云岩土和基性岩土，其中，黄棕壤为其地带性土壤。

该地区自然植被类型包括落叶阔叶林、常绿阔叶混交林和针叶纯林类型，针叶纯林主要以马尾松Pinus massoniana、黑松Pinus thunbergii和侧柏Platycladus orientalis为主，落叶阔叶林和常绿阔叶混交林主要以麻栎Quercus acutissima、黄连木Pistacia chinensis、青朴Celtis tetrandrassp、榆树Ulmus pumila、枫香Liquidambar formosana等为主。

根据林场森林的实际情况，按照不同林分年龄（31、35、40和55 a）和不同林分密度（0～250、250～500、500～750和750～1 000株/hm24个等级）要求，随机选取并设置了28块20 m×20 m的方形样地。

1.2 材料来源

在28块样地中，用围尺测量马尾松样木的根径和胸径，根径即树木距地面0米处的直径，用D0表示。用激光测高器测量样木树高，

本实验共收集了马尾松林木537株，主要测树因子分布范围见表1。剔除异常数据，剩余样木531株，其中21块样地共计404株样木用于建模，7块样地共计133株样木用于验模（见表1）。

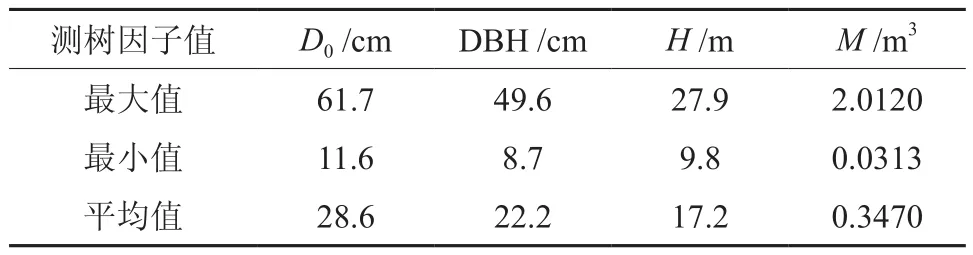
表1 马尾松样木的主要测树因子Table 1 Main tree-measuring factors of Pinus massoniana

1.3 研究方法

1.3.1 选用方程

1.3.1.1 一元非线性模型拟合

采用多模型选优法，通过选取线性、双曲线、三次曲线、指数、乘幂、对数、生长曲线、复合函数、倒数函数、S曲线和逻辑斯蒂11个方程来分别拟合马尾松林木根径和树高的相关关系，公式如下：

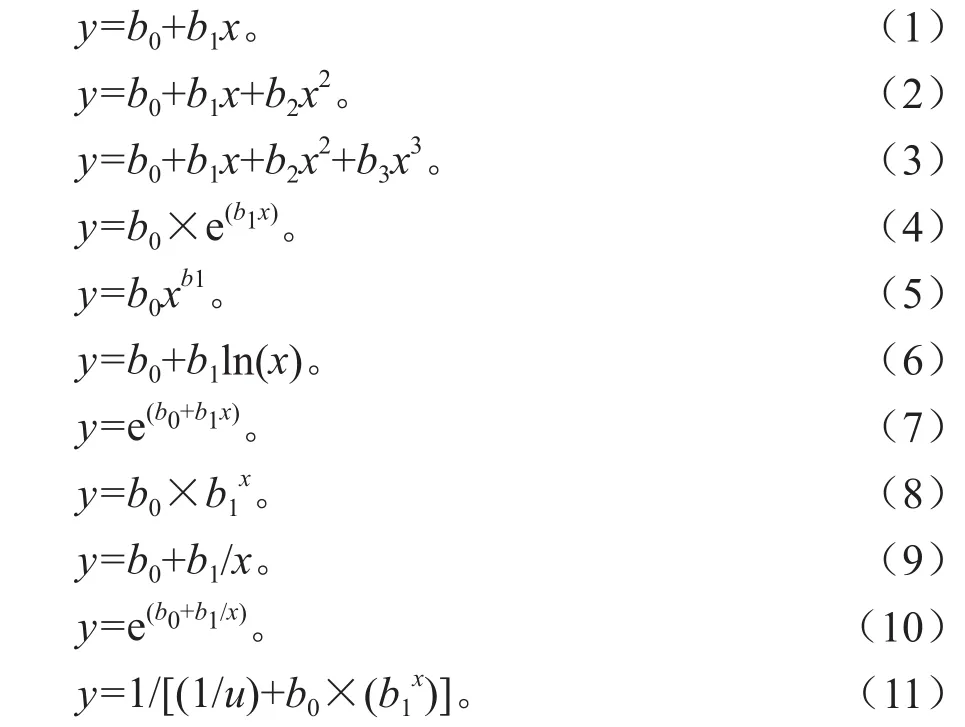
1.3.1.2 多元非线性混合效应模型拟合

为了考察林分密度、年龄等样地因子对根径和胸径关系模型参数的影响，在所建的乘幂函数模型的基础上，将其进行对数化处理，转化为线性方程，再采用多元混合效应模型的建模方法，加入各种样地因子，最终分别确定了以根径的对数、林分密度和林分年龄等因子为自变量，以胸径的对数为因变量的混合效应模型。

与普通多元回归模型不同，多元混合效应回归模型有微观和宏观两种方程，这里微观方程是指样木水平的方程，即将传统的二元材积方程线性化后的方程，宏观方程是指样地水平的方程，它以样木水平方程的系数为因变量，林分密度和林分年龄等因子为自变量建立的方程。公式如下：

式中：β0，β1分别为样木水平方程的截距和斜率，ε为样木水平方程的残差项，且ε～N(0，σ2)，γ00，γ01，γ02，γ03分别为模型参数，μ 为样地水平方程的残差项，且，本文用限制性最大似然法（REML）来估计两种方程残差的方差，并根据Wald统计量检验判断样木水平方程参数是否在样地水平上存在随机效应。

1.3.2 模型评价指标

1.3.2.1 型拟合效果评价

采用建模数据拟合模型，同时还应对模型的优劣进行评价，主要评价指标有相关指数（R2）、估计值的标准误（SEE）、平均预估误差（MPE）、总相对偏差（TRB）、平均相对误差（E）、平均相对误差绝对值（P）、赤池信息准则（AIC、AICC），-2 Res Log Likelihood 9个指标，公式如下：

式中，yi、和分别为方程变量的实测值、平均值和理论值，n为样木数，m为自变量个数。R2和SEE表示方程的拟合效果，R2值越大，SEE值越小，方程拟合效果越好，反之，亦然。MPE、TRB、E、P表示模型精度的大小，是衡量材积模型精度高低的常用指标。其中，TRB和E表示方程的平均相对误差大小，TRB和E越小，方程的相对误差越小，模型精度越高，反之，亦然。根据《林业专业调查主要技术规定》，立木材积的系统误差一般不得超过±3%。P排除了样本单元间正负误差的相互抵消，可反映对单木材积估计的误差水平，其值越小，单木材积估计的误差越小，模型精度越高。MPE反映平均材积估计值的误差大小，其值越小，平均材积估计的误差越小，模型精度越高。AIC、AICC和-2 Res Log Likelihood用于检验多元非线性混合效应模型的精度。在AIC和AICC中，l为对数似然值，k为被估计的参数个数，-2 Res Log Likelihood为模型近似似然值的-2倍。 AIC 、AICC和-2 Res Log Likelihood越小，表明模型拟合效果越好。

1.3.2.2 模型适应性检验

主要评价指标有以下几种：

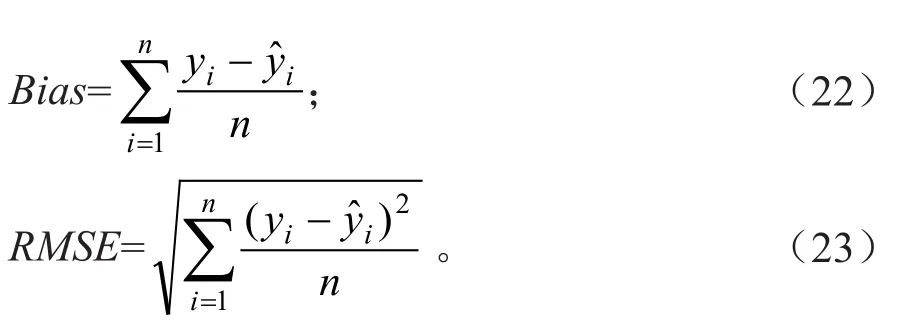
式中：Bias为绝对残差，RMSE为标准偏差。绝对残差和标准偏差越小，模型精度越高，反之，亦然。

1.3.3 数据处理

采用SPSS分析软件中一元非线性回归的方法分别拟合不同林木根径和胸径之间的相关关系。采用SAS分析软件的NLMIXED 模块分别建立根径和胸径的多元非线性混合效应模型。

2 结果与分析

2.1 传统的一元模型建立

2.1.1 一元模型拟合

采用线性、双曲线、三次曲线、指数、乘幂、对数、逻辑斯蒂等11个方程拟合了用于建模的404株样木的根径与胸径的相关关系，结果显示，所有模型的相关指数均大于0.8，表明林木根径和胸径有紧密的相关性，其中，线性、双曲线、三次曲线、乘幂方程拟合效果相对较好，相关指数均大于0.9（见表2）。

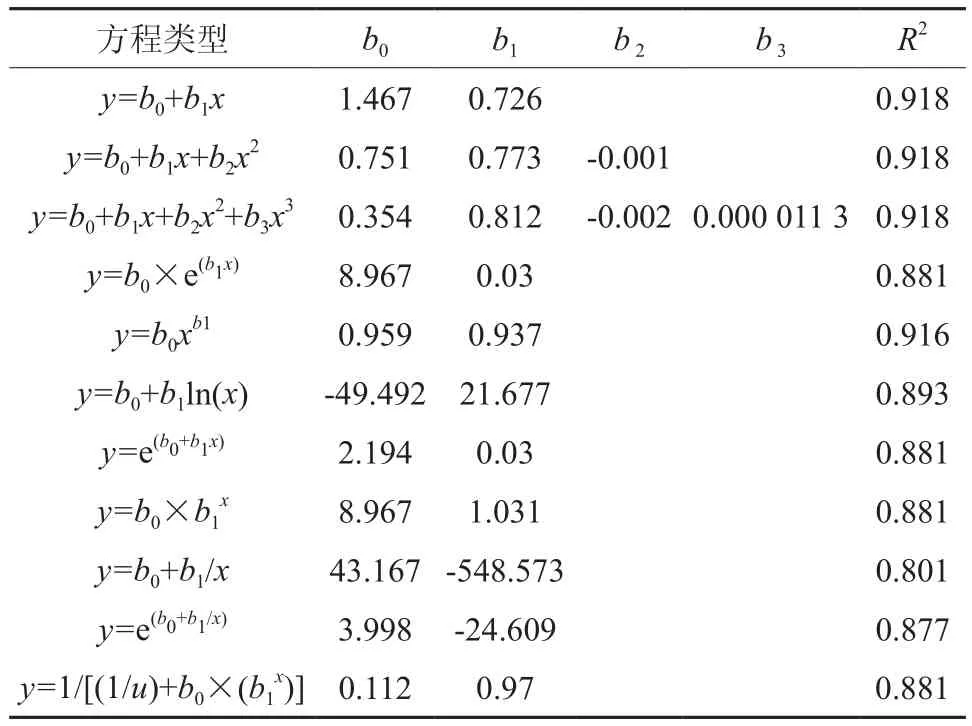
表2 一元模型参数Table 2 Parameters of monadic nonlinear models

根据相关指数大小，最终选出线性、双曲线、三次曲线、乘幂4种模型进行模型优度和精度检验。从表3可知，4个模型的平均相对误差和总相对偏差均小于3%，表明这些模型不存在趋势性的系统误差。4个模型的平均相对误差绝对值均小于10%，表明模型可精确地估计单株林木的胸径。与双曲线、三次曲线、乘幂方程相比，线性模型的相关指数较大（R2=0.919），估计值的标准误较小（SEE=1.854 8），平均预估误差（MPE=3.350 84）、总相对偏差（TRB=-1.34%）、平均相对误差（E=1.33%）和平均相对误差绝对值（P=7.734%）较小，表明线性方程的拟合优度和精度均较高。

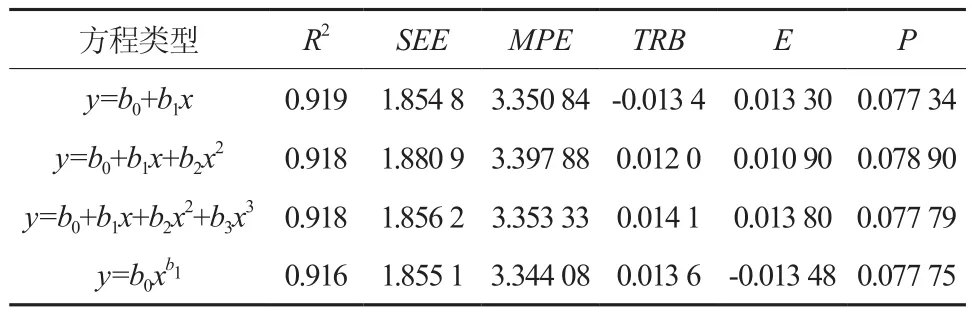
表3 根径与胸径的相关关系模型计算结果Table 3 Calculated results with mathematical models of ground diameters and DBH

2.1.2 一元模型适应性检验

马尾松根径和胸径关系模型是否适合于该地区，必须进行适应性检验。本文根据验模的133株马尾松样木资料，选用总相对偏差、绝对残差、标准偏差、平均相对误差、平均相对误差绝对值5个指标，对确定的根径和胸径相关关系模型进行适应性检验（见表4）。结果显示，线性、双曲线、三次曲线、乘幂4个模型的平均相对误差和总相对偏差均小于3%，表明这4个模型不存在趋势性的系统偏差。平均相对误差绝对值不超过10%，表明这4个模型用于估计该地区单株马尾松胸径的误差较小。适应性检验指标显示，线性模型的5个检验指标值均低于其他3个模型，表明线性模型的适应性最好。

综合模型拟合指标和适应性检验指标，对根径与胸径相关关系模型进行综合评价。结果显示，线性模型的相关指数最大，估计值的标准误、总相对偏差、平均预估误差、平均相对误差和平均相对误差绝对值、绝对残差、标准偏差均最小，表明线性模型拟合优度较好，精度较高，适用性较强。

表4 根径与胸径的相关关系模型适应性检验Table 4 Suitability test of the model related to ground diameters and DBH

2.2 多元非线性混合效应模型建立

2.2.1 多元非线性混合效应模型拟合

式中，γ00，γ01，γ02，β1分别为模型截距、林分年龄的参数、林分密度的参数和根径对数的参数，x1，x2，β1分别为林分年龄、林分密度和根径（d0）对数3个变量。根据Wald统计量检验，样木水平模型的截距（β0）随着样地的变化存在较为显著的随机效应（Pr Z=0.0644），斜率（β1）随着样地的变化不存在显著的随机效应。

根据自变量的参数可看出，马尾松林木的胸径与林分密度和林分年龄呈负相关，与根径呈正相关。从表5的相关指数（R2=0.950 4）、估计值的标准误（SEE=1.797 3）、平均预估误差（MPE=3.240 01）、总相对偏差（TRB=0.003 2）、平均相对误差（E=0.313%）和平均相对误差绝对值（P=5.642 8%）来看，与一元模型相比，混合效应模型拟合优度更高，模型精度更高，可较为精确地估计单木的胸径。

表5 根径与胸径的多元非线性混合效应模型计算结果†Table 5 Calculated results with multivariate nonlinear mixed effect models related to ground diameters and DBH

2.2.2 多元非线性混合效应模型适应性检验

通过采用平均相对误差、平均相对误差绝对值、总相对偏差、绝对残差、标准偏差5个指标对模型进行适应性检验（见表6），结果显示，总相对偏差、平均相对误差均小于1%，平均相对误差小于6%，从而表明该混合模型不存在趋势性的系统偏差，与一元线性模型相比，可更好地表达该地区马尾松林木根径与胸径的相关关系，模型具有较好的适应性。

表6 根径与胸径的多元混合效应模型的适应性检验Table 6 Suitability tests of multivariate nonlinear mixed effect models related to ground diameters and DBH

非线性混合模型的残差分布范围要比传统的一元线性回归模型小（见图1），说明考虑林分密度和林分年龄效应的非线性混合模型方法在预估胸径时比传统的一元回归模型精度更高。

图1 d0与胸径的一元线性模型（左）和多元混合效应模型（右）残差图像Fig.1 Residuals plot of Simple linear regression model (left) and multivariate nonlinear mixed effect model (right)related to ground diameter and DBH

3 结论与讨论

3.1 一元非线性模型

采用线性、双曲线、三次曲线、指数、乘幂、对数、生长曲线、复合函数、倒数函数、S曲线和逻辑斯蒂11个方程拟合了马尾松样木根径与胸径的相关关系，其中，线性、双曲线、三次曲线、乘幂4种模型的相关指数较大（R2＞0.9）。因此，选择线性、双曲线、三次曲线、乘幂4种模型进一步进行模型优度和精度检验。这4个模型的估计值的标准误较小（SEE＜2），平均相对误差和总相对偏差均小于3%，表明这些模型不存在趋势性的系统误差。平均相对误差绝对值均小于10%，表明4个模型可精确地估计单株林木的胸径，这与前人的研究有一定的一致性。张金全、李宝银等[7,10]认为，双曲线模型是拟合福建省建瓯市和沙县马尾松、杉木和阔叶树根径和胸径相关关系的最优模型。王华[8]研究发现，一元线性方程是拟合黔南地区马尾松根径和胸径相关关系的最佳模型。黎良财等[15]通过选用三次曲线、正弦、威布尔、线性等5个模型拟合了柳州市马尾松根径和胸径的相关关系，检验结果显示，三次曲线模型拟合效果最佳，精度最高。赵芳等[9]研究认为，双对数方程，即乘幂方程，是拟合福建延平区杉木根径和胸径相关关系的最佳模型。

但是，本研究的研究与前人的研究也有一定的差异。与双曲线、三次曲线、乘幂方程相比，线性模型的相关指数较大，估计值的标准误较小，平均预估误差、总相对偏差、平均相对误差和平均相对误差绝对值较小，表明线性方程的拟合优度和精度均最高，该结论与王华[8]的研究结果一致，但是与张金全、李宝银、黎良财等人[7,10,15]的研究结果不同，这可能与研究地区不同，所在气候类型和立地条件不同，树种不同，导致林木的生长也会出现差异，从而使得不同地区马尾松地径和胸径关系模型的拟合效果出现差异。

3.2 多元非线性混合效应模型

根据多元混合效应模型参数可看出，马尾松林木的胸径与林分密度和林分年龄呈负相关，与根径呈正相关，这是因为随着林分密度的增大，林木之间的平均距离减少，加速了林木对营养空间和营养资源的竞争，抑制了林木的径向生长[16]，因此，胸径会随林分密度的增加而减少。在模型中，虽然林分年龄与林木胸径呈负相关关系，但这种关系并不显著，只是为了提高模型整体精度才被保留。本文建立的传统一元模型已经说明了根径与胸径有紧密的正相关关系，这里就不再赘述。

多元混合效应模型的相关指数（R2=0.950 4）比传统的一元线性模型（R2=0.919）大，估计值的标准误（SEE=1.797 3）比传统的一元线性模型（SEE=1.854 8）小，表明多元混合效应模型的拟合优度高于传统的一元线性模型。多元混合效应模型的平均预估误差（MPE=3.240 01）、总相对偏差（TRB=0.003 2）、平均相对误差（E=0.003 13）、平均相对误差绝对值（P=0.056 428）比传统的一元线性模型（MPE=3.350 84，TRB=-0.013 4，E=0.013 3，P=0.077 34）小，表明多元混合效应模型的精度高于传统的一元线性模型。在适应性检验中，多元混合效应模型的平均相对误差（E=-0.088 8%）、平均相对误差绝对值（P=5.359 4%）、总相对偏差（TRB=0.035%）、绝对残差（Bias=0.058 55）、标准偏差（RMSE=1.509 94）较传统的一元线性模型 小（E=1.125%，P=7.464 5%，TRB=1.15%，Bias=0.050 62，RMSE=1.659 04），表明多元非线性混合效应模型的实用性强于传统的一元线性模型。

正是在传统一元乘幂模型的基础上，通过引入林分年龄、林分密度等样地因子，建立了以胸径为因变量、根径和林分年龄、林分密度等样地因子变量为自变量的多元混合效应模型。该模型不仅考虑了根径和胸径的紧密相关关系，而且考虑了林分年龄、林分密度等样地因子对根径和胸径相关关系的影响。因此，多元混合效应模型比传统一元模型的拟合效果更好，精度更高，适用性更强。

[1]沈家智.湿地松地径一元材积模型的研究[J].林业调查规划,1996, (1):12-15.

[2]彭桂永,陈明久,卓宁化.根径材积表编制方法的研究[J].林业勘察设计,2003,(1):1-3.

[3]李凤山,周 青, 屈志勇,等.贵州省柏木立木一元地径材积表的编制[J].四川林勘设计, 2000,(3):53-57.

[4]张江平,朱 松,夏忠胜,等.贵州省马尾松人工林地径材积模型研究[J].中南林业调查规划,2009,28(3):11-15.

[5]林 通.木荷一元材积表和地径材积表的研制[J].福建林业科技,2007,34(2): 97-101.

[6]杨艳丽,孙东祥,孙 福,等.大通地区主要树种胸径材积表改算地径材积表[J].青海大学学报（自然科学版）,1999,17(5): 29-30,36.

[7]张金全.建瓯市杉木与马尾松及阔叶树地径材积表的编制[J].现代农业科技,2012,(19):155-167,159.

[8]王 华.黔南地区马尾松根径材积式的建模与应用[J].贵州林业科技,2010,38(4):4-7.

[9]赵 芳,叶月兴.延平区杉木人工林地径材积表编制方法研究[J]. 福建林业科技,2006,33(1):72-75.

[10]李宝银,朱德培,江正铨,等.沙县杉木、马尾松、阔叶树地径一元材积表编制的研究[J].福建林业科技,1993,20(3):24-28.

[11]曾伟生. 利用误差变量联立方程组建立南方杉木一元立木材积模型和胸径地径回归模型[J].中南林业调查规划,2012,31(4): 1-4.

[12]林銮勇.福建柏地径一元材积表编制的探讨[J].林业勘查设计,1997,(2):4-6.

[13]王允寿,王健体,张 伟.山东省主要林分树种地径一元材积表的编制[J]. 山东林业科技,1998,(1):35-36.

[14]刘 健,陈平留,陈昌雄.闽北主要用材树种胸径与去皮地径关系的研究[J].福建林学院学报,1996,16(1):45-48.

[15]黎良财, 邓 利. 柳州市马尾松地径一元材积表的编制[J].林业调查规划,2011,36(1):1-3.

[16]李伟伟.林分密度及立地条件对华北落叶松人工林影响的研究——以塞罕坝机械林场为例[D].保定:河北农业大学,2009.

Research on the multivariate mixed effect model of different ground diameters and DBHs of Pinus massoniana in Nanjing

ZHAO Hao-yan1, ZHANG Min-xia1, ZHANG Jie1, FANG Yan1, SHAO Chang-sheng2, CHEN Ge-ping1
(1. Nanjing Forest Police College, Nanjing 210023, Jiangsu, China;2.Laoshan State Forest Farm of Nanjing City, Nanjing 211811, Jiangsu, China)

In order to describe the relation between ground diameters and diameters at breast height (DBH) of Pinus massoniana Lamb trees in Nanjing, related mathematical models were established with 11 monadic models (linear equation, power equation,hyperbolic equation and so on) and multivariate nonlinear mixed effect model based on the data of 531 Pinus massoniana Lamb trees from 28 20 m×20 m square plots. The results reveal that the correlation indexes of all monadic models were more than 0.8, the fit goodness of monadic linear model was best (R2=0.919, SEE=1.8548), and the values of TRB, E and P (TRB=-1.34%, E=1.33%,P=7.734%) were least in all monadic models. The adaptability test shows that the monadic linear model has more widespread suitability(E=1.125%, P=7.4645%). The established multivariate nonlinear mixed effect model has higher accuracy and fit goodness compared to monadic linear model (R2=0.9504, SEE=1.7973, TRB=0.32%, E=0.313%, P=5.6428%). The suitability test reveals that the multivariate nonlinear mixed effect model has more widespread application (E=-0.0888%, P=5.3594%), which indicates the multivariate mixed effect model can fit more precisely the relation between ground diameters (d0) and DBHs of Pinus massoniana Lamb trees in Nanjing than monadic linear model .

Pinus massoniana; ground diameter; DBH; monadic linear model; multivariate nonlinear mixed effect model

S758.1

A

1673-923X(2015)11-0043-06

10.14067/j.cnki.1673-923x.2015.11.009

2015-09-15

中央高校项目（LGYB201401）；948项目（2015-4-14）；南京森林警察学院精品课程培育项目（2015205）

赵浩彦，讲师，博士

张民侠，副教授，博士；E-mail：76697464@qq.com

赵浩彦，张民侠，张 洁，等.南京马尾松根径与胸径多元混合效应模型研建[J]. 中南林业科技大学学报，2015, 35(11):43-48, 67.

[本文编校：吴 毅]