软硬件协同设计实现LTE关键算法的方法
沈苑宜,吴紫盛,李笑天,何 虎
(清华大学 微电子所,北京100084)
0 引 言
3GPP机构为了提高数据速率、低延迟,在2005 年确定了长期演进 (LTE)的技术规范[1]。为了在有限带宽下提高数据传输的效率,LTE 中引入了正交频分复用技术(OFDM)作为下行链路传输方案[2]。采用这一技术后,固定带宽上可以同时使用更多的子载波,因而能够传输更多的数据,但同时也使得信号的处理变得更为复杂。这也就对信号运算处理提出了更高的要求。用数字信号处理器(DSP)处理LTE 的算法能够有效提高系统的传输速度。当前主流的处理器架构有两种:超标量 (superscaler)和超长指令字 (VLIW)。结合两种结构各自的优点,清华大学微电子所DSP实验室设计出一款面向通信、媒体算法支持超标量和超长指令字的双模式混合架构处理器——Lily2[3]。为了在Lily2处理器上高效运行LTE 系统,需要考虑处理器的特殊性能,做相应的应用调整。
本文选取LTE 中的OFDM 发射机和信道估计模块,采用了软硬件协同设计的方法,利用gem5模拟器仿真,从算法层面和处理器层面不断迭代优化调整,直到得到较好的结果。实验结果表明该方法有效提升了通信模块在处理器上的运行效率,也进一步优化了处理器的性能。
1 相关工作
1.1 LTE物理层介绍
LTE下行物理信道处理一般过程如图1所示。LTE 物理层在发射端对MAC 层接收来的信号进行编码、加扰、调制、映射后转换为OFDM 信号在信道上传输[4],在接收端对这些信号进行解调、信道估计、解码解扰等操作来恢复。LTE中引入正交频分复用技术 (OFDM)使得在相同的带宽上传输更多的子载波[5],从而增大了传输的数据量。这也意味着OFDM 信号的处理需要采用较优的算法和处理器加速运算。

图1 下行物理信道处理过程
1.2 LTE中的关键算法
本文根据LTE 物理层建模分析的结果,发现LTE 物理层的性能瓶颈主要集中在OFDM 信号处理的部分,包括OFDM 发射机、接收机、信道估计等。本文选取其中OFDM 发射机和信道估计这两个模块做具体研究。
1.2.1 OFDM 发射机
OFDM 发射机将每个时隙的信号映射到资源栅格上,再经过一系列处理并调制后生成OFDM 信号。OFDM 发射机的流程如图2所示。资源粒子映射后需要将频域上的每列调制成频率间隔的子载波,此过程是实现固定带宽传输更多信号的关键。调制过程可采用快速傅里叶逆变换 (IFFT)高效实现。最常见的FFT 算法有Cooley-Tukey 算法[6]。它采用分治的方法,将长度为N 的序列分成两个N/2序列递归运算[7,8],可将离散傅里叶变换 (DFT)的时间复杂度O(n2)降为O(NlogN)。

图2 OFDM 发射机结构
1.2.2 信道估计
接收端信号解调后乘以信道响应的共轭可以解码发送信号[9,10]。为了能正确解码信号,需要精确估计信道频域响应。常见的估计算法有盲估计、根据导频信号来估计的最小二乘估计算法 (LS)和线性最小均方差估计算法(LMMSE)[11]。LMMSE算法具有较高的准确率,它根据求导频信号的最小均方误差来获得信道响应的估计值,计算公式为
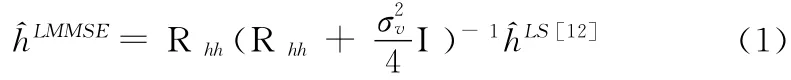
因为LMMSE需要进行复数矩阵求逆运算,导致运算复杂度较高。
LMMSE算法中求逆矩阵的大小和天线数有关,本文采用的两天线的OFDM-MIMO 系统矩阵大小为4×4。目前矩阵求逆最快算法的复杂度为O(n2.37)[13],但不适用于加速小型矩阵求逆。常见的矩阵求逆算法有高斯消元法、LUP分解法[14]、正交分解法,算法复杂度均为O(n3)。
1.3 Lily2处理器介绍
Lily2处理器是一款面向媒体信号处理的高性能数字信号处理器,架构如图3所示。它包含6个独立的功能单元,每个时钟周期可并行执行6条指令,采用完全自主知识产权的指令集,支持superscalar和超长指令字 (VLIW)两种执行模式。在superscalar模式下,处理器一个周期执行一或两条指令,汇编指令可直接由编译器生成;在VLIW模式下,X 簇和Y 簇的3个功能单元可并行运行,因而一个周期可最多执行6条,执行效率更高,但由于编译器生成代码存在较大难度,需要程序员手写汇编程序。此外,处理器包含了3个不同的功能单元算术逻辑功能单元.A,乘法、浮点、浮点矢量功能单元.M,数据传输功能单元.D。片内集成了一个全局寄存器堆和两个本地寄存器堆。全局寄存器堆包含8个128位矢量寄存器,本地寄存器X 包含24个32位通用寄存器,Y 包含24个128位矢量寄存器。
Gem5模拟器是一款模式化的离散时间驱动全系统模拟器。它支持周期精度级别的仿真,且高度可配置、集成多种ISA 和多种CPU 模型,对自定义指令集架构处理器模型也可进行全定制的开发。使用Gem5 模拟器,不仅可以方便的搭建Lily2,也使修改和优化更便捷。
2 LTE算法在处理器上的实现
本文采用软硬件协同设计的方法[15],在Lily2 处理器上高效的实现LTE 中的OFDM 发射机和信道估计两个模块。方法如图4所示,首先从算法的角度,对这两个算法进行分析,找到其中运算量较大的部分,再针对这些性能瓶颈从算法上做一些调整和优化。然后从处理器的角度做进一步的优化。针对通信算法中的一些操作,指令集可能并不完备,需要增加或者调整一些指令,使算法能在处理器上更快的运行。在算法的实现和指令集的修改中,可能会发现处理器结构上的一些问题,最后再从处理器结构上做一些调整。此后,算法的性能可能仍然低于期望,这时就需要继续分析性能,找到瓶颈所在,从算法和处理器上再针对瓶颈做优化调整。如此迭代,直到得到期望性能。
2.1 LTE算法的实现和优化
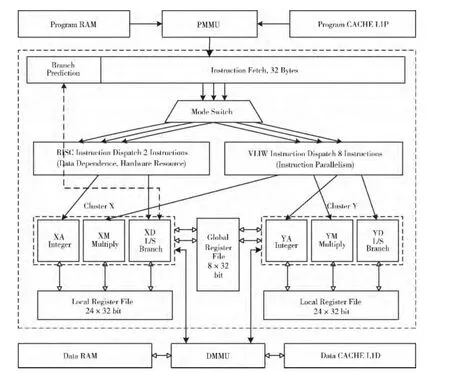
图3 Lily2总架构
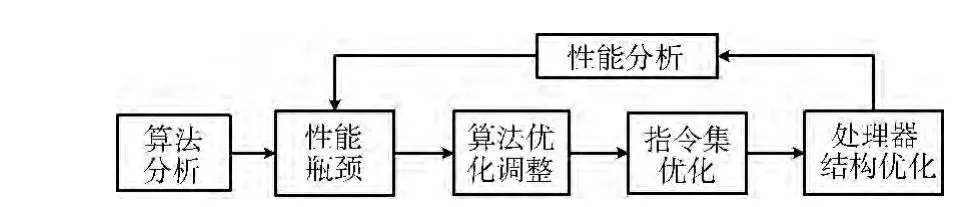
图4 软硬件协同设计流程
OFDM 发射机和信道估计算法中,有些部分运算量很大,比如FFT,有些部分就不涉及数学运算。本文考虑利用Lily2双模式的特性,对运算量大、复杂度高的部分在超长指令字模式下手写汇编程序并重点优化,而对其它部分在superscalar模式下用编译器直接生成代码。
2.1.1 OFDM 发射机
OFDM 发射机中资源粒子映射,插入导频等操作不涉及任何数学运算。而快速傅里叶变换 (FFT)则涉及大量的数学运算,需要重点优化。FFT 的运算是将一组数通过乘加运算后重排序,输出新的一组数,需要用到大量的乘法和加减法运算。FFT 根据基底的不同,可分为二、四、八甚至混合基底。基底越大所需的复数乘法和占用的内存越小,但却增大了实数乘法和实现的复杂度。以4为基底的快速傅里叶变换有较优的性能,主流的处理器如TI公司的C64x+都会选用。本文也选择4基底的FFT,它的运算结构如图5所示。LTE 中的快速傅里叶变换处理的是浮点复数,本文浮点数精度为32位,将实部和虚部看为两个单独的操作数,按照先实部后虚部交织的方式排列。
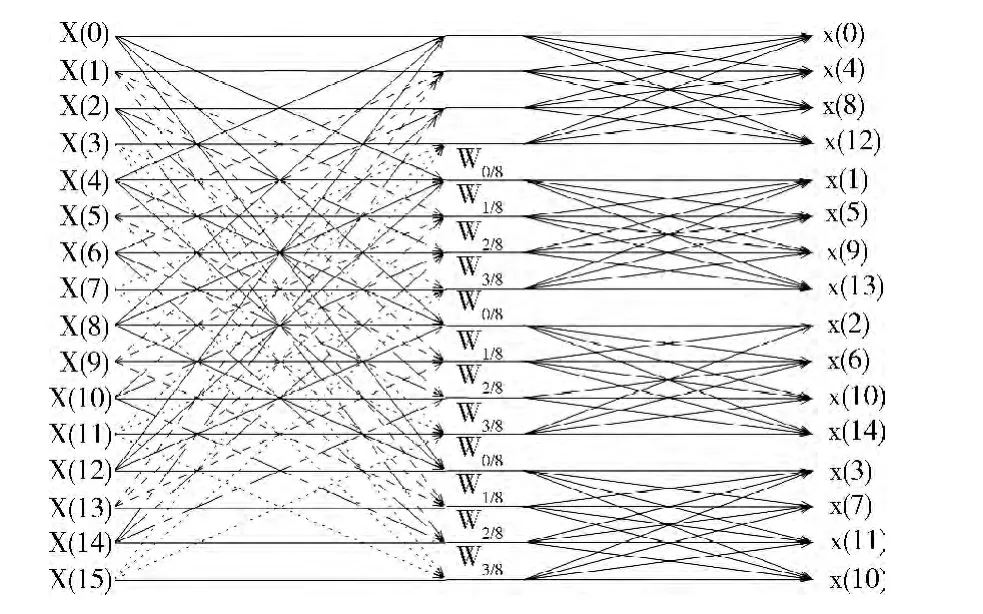
图5 十六点基四FFT 蝶形运算
实现该算法需要用到3层循环:第1层主要进行移位运算,决定FFT 序列需要几轮的运算;第2层求旋转因子WnkN,即求三角函数值;在第3 层计算傅里叶变换的值。第1层循环的次数是log4N,第2层和第3层循环合并后的循环次数为N/4。若第2层循环N/4次,则最内层循环一次。Cooley-Tukey算法中最内层循环计算的点数为4。
Lily2处理器支持向量指令,可以同时处理4个32 位单精度浮点数。向量指令总的效率比非向量指令要高很多,使用向量指令对算法有明显的加速。为了全面的利用向量指令,保证每条向量指令处理4个浮点数,本文将Cooley-Tukey算法中最内层循环计算的点数由4增大到8,也就是将第2层循环展开1层。
2.1.2 信道估计
信道估计的过程为:先收集导频信号,组成导频矩阵,再按照式 (1)对矩阵进行乘法和求逆运算计算导频估计矩阵,最后再通过时域、频域插值将求得的导频估计矩阵扩展为信道估计矩阵。其中运算量较大的运算有矩阵求逆和矩阵乘法。而矩阵求逆计算量高于矩阵乘法,本文就矩阵求逆做重点研究。
矩阵求逆需要用到除法运算,而在处理器中浮点除法运算时间远长于浮点乘法,减少除法运算成为优化矩阵求逆的关键。虽然常见的矩阵求逆运算的复杂度都为O(n3),但具体的乘法、除法和加减法运算次数不同。分析3种常见的矩阵求逆算法,如表1,可以发现高斯消元法和正交分解法的除法次数较少,而高斯消元法的乘法、加减法运算次数要少于正交分解法。因此本文采用高斯消元法。此处矩阵求逆处理的也是浮点复数,浮点数的精度是32位,采用先实部后虚部交织排列的方式。

表1 矩阵求逆算法计算量
3 处理器的优化
3.1 指令集的优化
LTE算法在处理器上的实现大量运用了浮点向量指令。Lily2处理器具有较全面的浮点向量计算指令,但是缺少针对向量寄存器中的操作数进行移动和交换等操作的指令,比如从向量寄存器中提取某一个32位数存入通用寄存器,以及将通用寄存器中的值存入向量寄存器的某位,或者交换向量寄存器中数的位置,合并两个向量寄存器等,如图6所示。
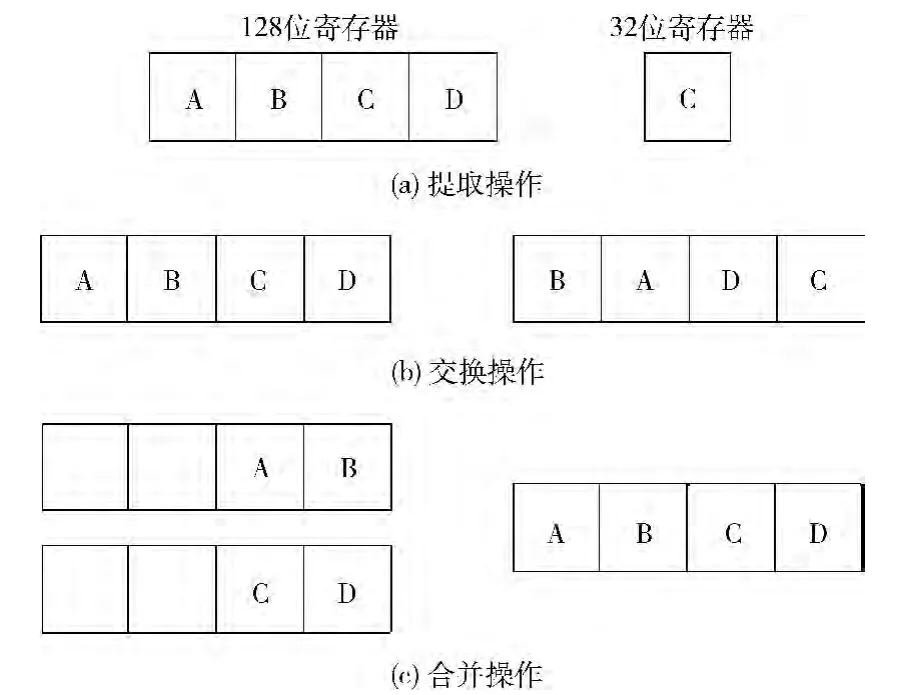
图6 各向量指令操作
复数的实部和虚部是交织排列的,而LTE 算法处理尤其是快速傅里叶变换过程中,两个复数之间的计算是交叉的,比如复数A的实部与复数B相减,复数A 的虚部与复数B相加。在使用向量指令时,需要以4个数为单位进行相同运算,那么往往就需要对这些复数重新进行组合。缺少针对向量操作数的指令,会使得向量指令整体的效率降低。
因此本文增加如下指令,以提高向量指令使用的效率和灵活性:MOV.FQ 和MOV.QF 两条用于向量寄存器和通用寄存器见交互的指令;一条SWAP 指令用于向量寄存器 间 数 据 的 交 换;PACKEVENSP,PACKODDSP,QPACKL,QPACKH 这4条用于合并向量寄存器的指令。
Lily2处理器分为X 簇和Y 簇,而每一簇内都集成了3个不同的功能单元,所以在超长指令字模式下一个周期内可以同时运行6条指令。浮点的运算主要集中在乘法、浮点、浮点矢量功能单元.M。在浮点向量计算集中的地方,如FFT 算法的最内层循环,就往往只有.M 这一个功能单元在运行,导致指令的并行度不高。为了提高指令的并行度,增加算法整体的运行效率,可将部分常见指令移到其它功能单元,如.D 单元。所以本文将浮点向量加法和减法指令从.M 单元移到了.D 单元,使得一个周期内可以运行尽可能多的功能单元。
3.2 处理器结构的优化
处理器一周期同时执行6 条指令的时候,也就是有6个功能单元同时运行的时候,处理器执行的效率最高。为了让尽可能多的功能单元同时执行,不仅需要保证使用不同类型的功能单元,还需要保证X 簇和Y 簇能较为均等的使用。X 簇和Y 簇寄存器之间的交互可通过全局寄存器。全局寄存器既可以和X 簇寄存器也可以和Y 簇寄存器交互,通过全局寄存器可以完成X、Y 间的互通。但是全局寄存器的数量比较有限,为满足全局寄存器的分配,就会舍弃使用一部分X 簇寄存器或者Y 簇寄存器,这样就使得指令并行度的下降。为了提高指令的并行度,让X 簇寄存器和Y 簇寄存器可以更为均等的使用,本文增加了X 簇和Y 簇寄存器之间直接互通的通道,如图7所示,也增加了MOVYX和MOVXY 这两条指令用于实现将X 寄存器的值移至Y 寄存器和将Y 寄存器的值移至X 寄存器。这样就保证了X 簇和Y 簇能够均等的使用。
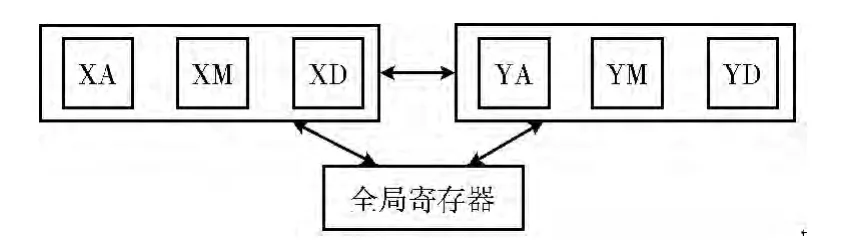
图7 X 簇和Y 簇交互
4 性能分析与对比
本文利用在gem5模拟器上搭建的Lily2处理器来运行汇编程序,并且也在模拟器上对指令集、处理器结构做了修改,最后统计了每次优化后模拟器上运行的周期数。
每一次的优化,在性能上都有较为明显的提升,以FFT 为例的结果如图8所示。其中,需要说明的是原始的结果是superscalar模式下手写汇编并且未使用向量指令得出的;最后结果中5651个周期是输入数据的读入,不记入FFT 运行的周期数。对比superscalar和超长指令字模式下FFT 的周期数,可以发现性能提高了近一倍,说明在超长指令字模式对算法的加速很明显。算法层面的优化有很明显的效果,最原始的结果,即未使用向量指令和循环展开使用向量指令后,周期数减少了1/3左右。处理器上的优化,包括指令集的修改和处理器结构的调整,也使性能有较为明显的提升。指令集的优化使得周期数减少了10 000左右,处理器结构的优化也使周期数减少了近10 000。
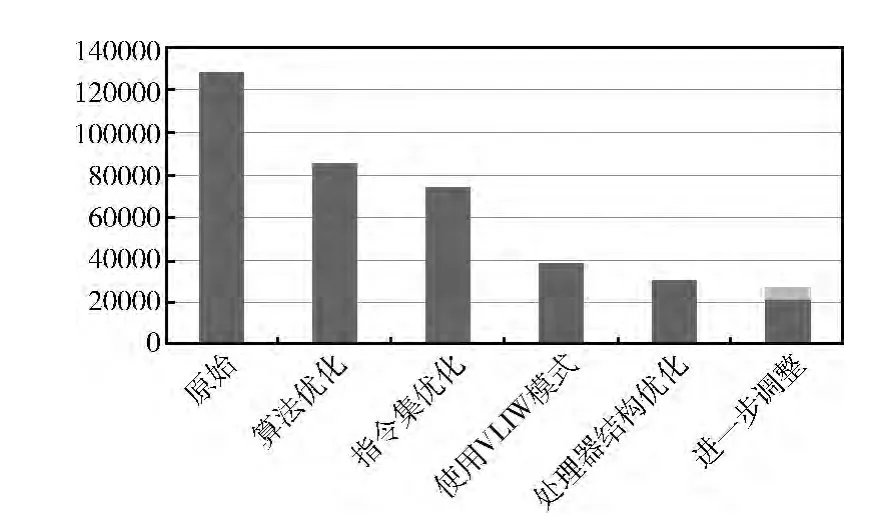
图8 性能分析对比
计算每周期执行的指令数 (IPC),也显示出Lily2处理器良好的性能。FFT 的IPC可达2.2,矩阵求逆为1.6。
本文将改进后的FFT 和矩阵求逆算法与Texas Instrument公司的DSP产品进行了对比,见表2。C674是TI公司2013年最新的一款DSP,可以看到Lily2 的性能介于C674和C67之间,并且很接近C674。对于矩阵求逆,TI公司的矩阵求逆算法是用16位浮点数实现,执行周期数为273[16],本文采用的是32位浮点数,其结果的准确度远高于16位浮点数,执行周期数为1584。

表2 Lily2与主流处理器性能对比
5 结束语
本文在数字信号处理器上有效实现了LTE 中的关键算法,并通过软硬件协同设计的方法,对这些算法从算法层面和处理器层面进行了优化,一方面提升了通信算法在处理器上运行的效率,另一方面也提升了处理器处理通信系统的性能。从执行周期数上来看,优化后算法的性能可与主流的处理器相比。最终结果不仅显示了处理器处理LTE通信算法有良好的性能,也表明软硬件协同优化的方法对提高算法执行效率有良好的作用。
[1]Fazel K,Kaiser S.Multi-carrier and spread spectrum systems:From OFDM and MC-CDMA to LTE and WiMAX [M].Wiley,2008.
[2]Dahlman E,Parkvall S,Skold J,et al.3Gevolution:HSPA and LTE for mobile broadband [M].Academic Press,2010.
[3]Shen Z,He H,Yang X,et al.Architecture design of a variable length instruction set VLIW DSP [J].Tsinghua Science &Technology,2009,14 (5):561-569.
[4]Cho YS,Kim J,Yang WY,et al.MIMO-OFDM wireless communications with MATLAB [M].John Wiley &Sons,2010.
[5]LTE:The UMTS long term evolution [M].New York:John Wiley &Sons,2009.
[6]Rao K,Kim DN,Hwang JJ.Fast Fourier transform-algorithms and applications:Algorithms and applications [M].Springer,2011.
[7]FENG Hualiang.FFT implementation on TMS320C64x+DSP[R].Texas Instrument,2012 (in Chinese). [冯华亮.基于TMS320C64x+DSP的FFT 实现 [R].德州仪器,2012.]
[8]Saeed A,Elbably M,Abdelfadeel G,et al.Efficient FPGA implementation of FFT/IFFT processor [J].International Journal of Circuits,Systems and Signal Processing,2009,3(3):103-110.
[9]Dahlman E,Parkvall S,Skold J.4G:LTE/LTE-advanced for mobile broadband [M].Academic Press,2013.
[10]Holma Harri,Toskala Antti.LTE for UMTS-OFDMA and SC-FDMA based radio access [M ].John Wiley &Sons,2009.
[11]Halunga SV,Vizireanu N.Performance evaluation for conventional and MMSE multiuser detection algorithms in imperfect reception conditions [J].Digital Signal Processing,2010,20 (1):166-178.
[12]Mehlfuhrer C,Caban S,Rupp M.An accurate and low complex channel estimator for OFDM WiMAX [C]//3rd International Symposium on Communications,Control and Signal Processing.IEEE,2008:922-926.
[13]Sastry SS.Introductory methods of numerical analysis[M].PHI Learning Pvt Ltd,2012.
[14]Parhami B.Computer arithmetic:Algorithms and hardware designs[M].Oxford University Press Inc,2009.
[15]Schaumont PR.A practical introduction to hardware/software codesign [M].Springer,2012.
[16]Yan M,Feng B,Song T.On matrix inversion for LTE MIMO applications using Texas instruments floating point DSP[C]//IEEE 10th International Conference on Signal Processing.IEEE,2010:633-636.

