面向机场噪声预测的多噪声因素航迹聚类

吕宗平，李永祥，徐 涛，2

（1.中国民航信息技术科研基地，天津300300；2.中国民航大学 计算机科学与技术学院，天津300300）

0 引 言

为了更好地对机场噪声的影响范围及其监测点的噪声值进行评估和预测，结合航迹数据、飞行速度、飞机机型数据等机场噪声主要影响因素进行航迹聚类。研究每一簇内的航迹噪声影响范围和监测点噪声影响值是否相似，为机场噪声预测提供理论与技术支持尤为重要。因此，开展航迹聚类研究有着十分重要的应用价值。

由于机场跑道资源有限，机场流量拥堵，使得机场空域流量拥挤和航班延误严重，Frank等提出了基于航迹点比对进行航迹聚类［1］，更好地规划空域内的飞行程序，从而减少空域拥堵和航班延误；Gariel等提出了基于最长公共子序列的相似性度量算法，并把聚类结果应用到异常航迹预警［2］；王超等改进了Frank等的算法，提出根据前后附近航迹点最短距离来度量航迹相似性，将聚类结果应用到终端区的进场程序管制［3］，缓解管制员的压力，从而保障机场的飞行安全；王洁宁等提出了基于时间空间的航迹聚类分析［4］，聚类结果符合管制指挥的实际情况，从而保障了空中交通管制的飞行安全，提高了航班的运行效率。

上述研究者提出的航迹聚类思想不适合作为研究航迹聚类在机场噪声预测上的应用。因此，本文提出一种基于航迹间面积的相似性度量方法，结合航迹数据和机场噪声主要影响因素数据，构建适合机场噪声预测的多噪声影响因素航迹聚类模型。

1 基本概念

1.1 航迹的特征与表示

航迹数据是由空管部门提供的机场进近雷达数据，原始雷达数据有很多错误、缺失等脏数据，且包含对噪声影响评估分析无用的属性。因此，需要对原始雷达数据进行数据筛选，选择重要数据属性和完整正确的航迹信息。表1给出了一个航班按照时间顺序排序后的一部分航迹数据。

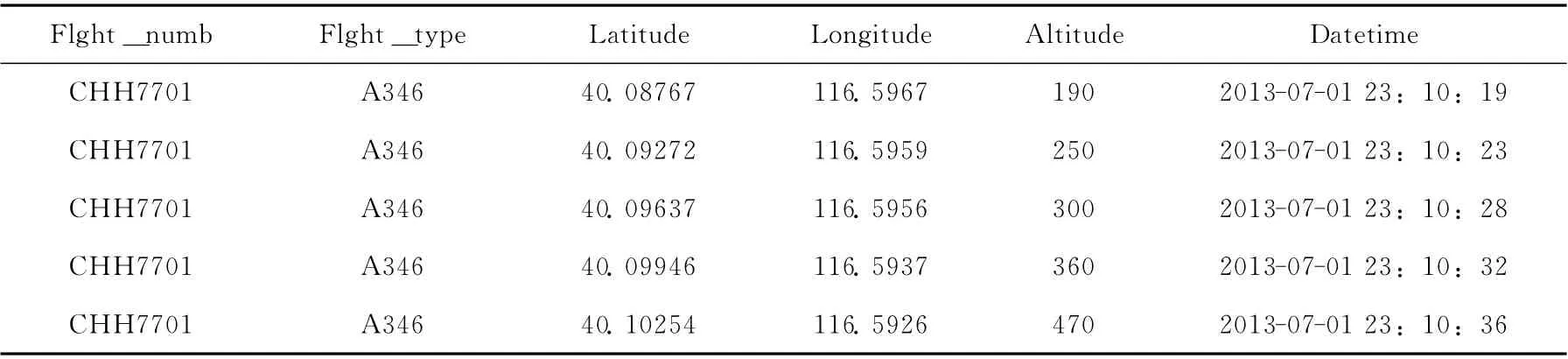
表1 一架航班的航迹数据片段

由表1中数据可知，每一个航班号对应着一条航迹信息，包括机型、经纬度、海拔高度等。分析航迹点记录时刻可知每个航迹点之间的时间间隔是4s～5s（由雷达的扫描周期决定），所以每一条航迹是由不同数目的离散航迹点组成。

不失一般性，航迹集合可表示为如下集合形式

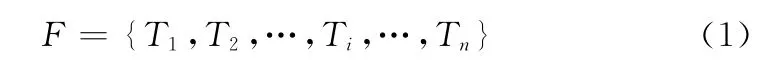
式中：Ti——第i条航迹，i∈［1，n］为航迹编号，n 为航迹总条数。Ti可用航迹点的数据集表征

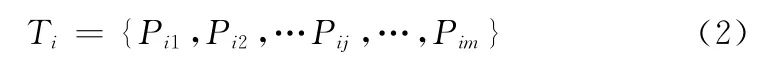
式中：Pij——第i条航迹中第j 个航迹点的信息，j∈［1，m］为航迹点编号，m 为航迹中航迹点总数。

每一个航迹点Pij定义为一个四维向量

式中：x、y、z、t——第i条航迹中第j 个航迹点的横坐标纬度，纵坐标经度，海拔高度和航迹点记录时间，分别用pij（x）、pij（y）、pij（z）、pij（t）表示。

根据 “环境影响评价技术导则：声环境”［5］，发动机推力是飞机产生噪声的最大因素，由飞机噪声和性能数据库（aircraft noise and performance，ANP）得到的发动 机推力数据是标准的飞机性能参数，航班实际飞行时由于载客量不同，所使用的实际推力也随之不同。以此，根据每一航班的雷达航迹数据用航迹段内的飞机起飞时的速度、航迹点结束时的飞机速度、平均速度、最大速度、最小速度来评估每一条航迹的真实飞行速度情况。

航迹集合F 对应的飞行速度集合V 定义为如下集合形式

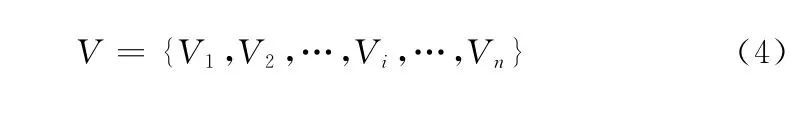
其中，每一条航迹的速度集合Vi可表示为如下集合形式

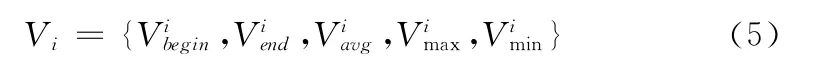
式中：Vi——第Ti条 航 迹 的 速 度 集 合，、、、、——航迹段内的起始速度、最后速度、平均速度、最大速度和最小速度。

1.2 发动机推力

飞机发动机推力数据由ANP数据库中获取的包括飞机性能参数 （如最大起飞重量、最大起飞距离、最大起飞推力、最大爬升推力等），以及飞机噪声功率距离 （noise power distance，NPD）数据。因此，通过ANP数据库可以获取飞机所必须的发动机各项性能，从中筛选出现有117种常用机型的性能参数。由于所考虑的离港航迹在机场进近管制区域内，飞机会经历起飞和爬升两个阶段，因此，选取最大爬升、最大起飞推力数据代表该机型的整体性能（见表2）。

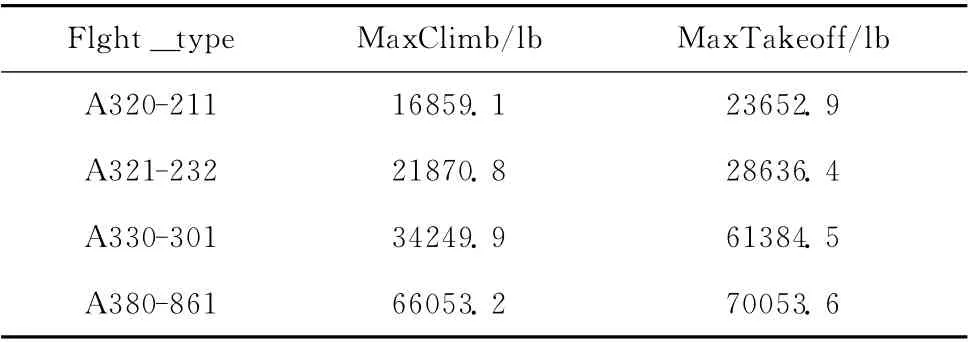
表2 飞机发动机推力

不失一般性，机型集合可表示为如下集合形式

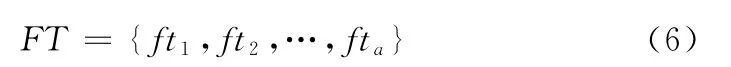
式中：a——机型数目，机型推力可表示为

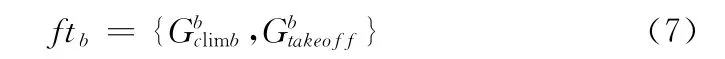
2 面向机场噪声预测的多噪声影响因素航迹聚类模型

2.1 基于航迹间面积的航迹相似性度量方法

设Ti＝｛Pi1，Pi2，…Pie…，Pik｝和Tj＝ ｛Pj1，Pj2，…Pjq…，Pjl｝是任意的两条航迹。记Strace为Ti、Tj两条航迹之间围成的面积。从图1可见，图1 （a）与图1 （b）中的航迹间面积Strace非常相似，但航迹的方向不一致。通过增加对惩罚弧形面积Sarc的分析，能够很好地忽略航迹方向不一致和飞机速度不同对航迹相似性的影响，使得航迹之间的相似性度量更加精细。

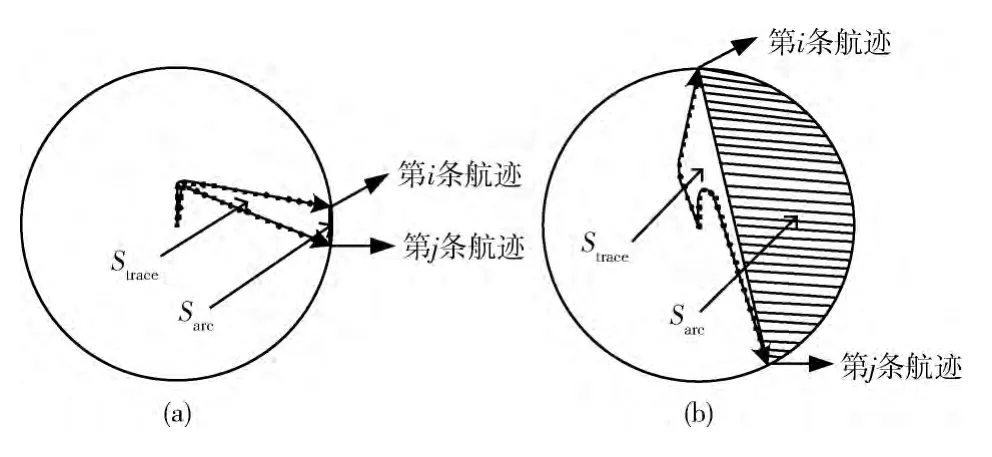
图1 基于航迹间面积的航迹相似性度量方法

航迹间的相似性度量函数由两条航迹之间的面积Strace和惩罚弧形面积Sarc组成 （如图2所示）。

实际航迹间的面积由若干三角形面积组成。已知P1，P2，P3三点坐标围成的三角形面积为

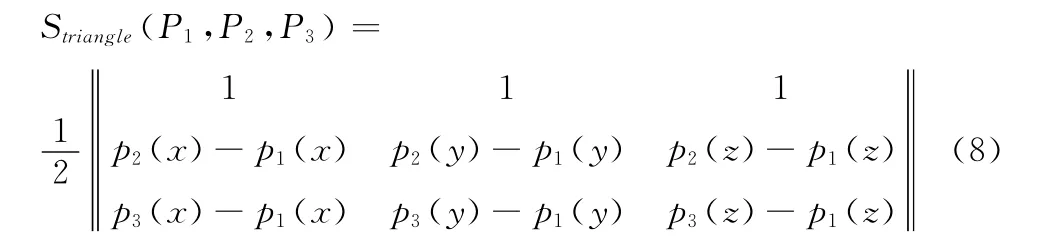
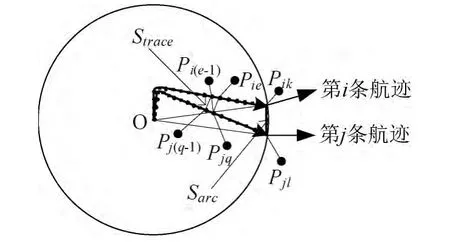
图2 航迹间面积计算过程

惩罚弧形面积由扇形面积减去其对应的三角形面积

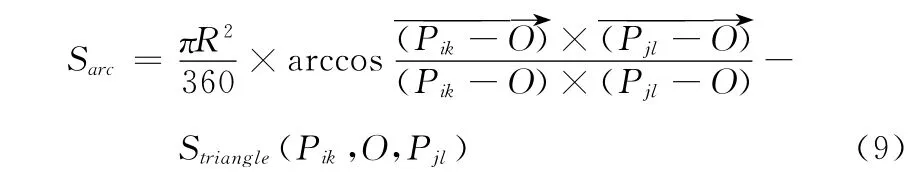
于是，基于航迹间面积的航迹相似性度量函数d（Ti，Tj）及航迹间的相似性矩阵R1为

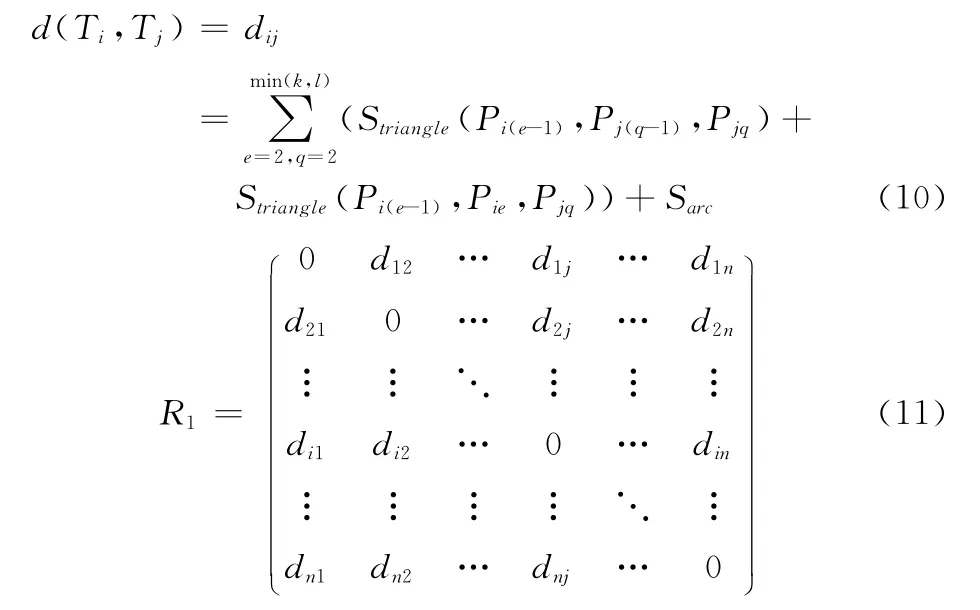
2.2 加权K－medoids航迹聚类算法

考虑到每一条航迹数据由一系列的航迹点组成，航迹点数目可能各不相同，不具备典型的数据与属性之间的对应关系特征，因此，本文选用基于划分的聚类算法［6］对满足指定条件的航迹数据集进行航迹相似度聚类分析。由于航迹的离散性，属性加权K－medoids算法［7］在航迹簇中选取真实的航迹作为簇中心，能很好地结合航迹数据、飞行速度信息进行聚类，而航迹速度V 所占比重不能太大，因此采用属性加权的K－medoids算法 （见表3）。

表3 加权K－medoids航迹聚类算法

2.3 多噪声影响因素航迹聚类流程

航迹决定噪声的分布范围，飞行速度、机型等决定噪声值的大小。图3中对航迹、航迹段内飞机飞行速度进行聚类。根据航迹数据集合F 计算航迹的真实飞行速度数据集V。对航迹数据集合采用航迹间面积的相似性度量方法计算航迹之间的相似性矩阵R1，航迹速度集合采用欧几里德距离计算每两条航迹之间的速度相似性矩阵R2，分别对相似性矩阵R1、R2数据归一化，采用属性加权的K－medoids算法［9］对航迹数据集合和航迹速度集合聚类分析。

传统的机型分类按照机型体积与载客量不同分为大、中、小型机，该分类比较粗糙，不适合作为机场噪声预测上的机型分类标准。因此本文采用K－means聚类算法［10］对1.2节中的发动机推力数据作进一步聚类分析。

对航迹和飞机飞行速度聚类结果按照机型聚类结果进一步划分，使航迹簇内的航迹噪声影响范围和噪声影响值都非常相似。

综上所述，面向机场噪声预测的多噪声影响因素航迹聚类流程 （如图3所示）。

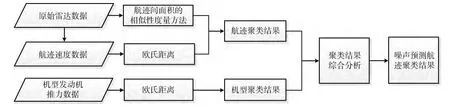
图3 面向机场噪声预测的多噪声影响因素航迹聚类流程

3 实验结果与分析

为了验证多噪声影响因素航迹聚类模型的合理性和正确性，根据2.3节中的多噪声影响因素航迹聚类模型，把得到的最终航迹聚类结果导入INM 噪声预测软件，分别绘制每一条航迹的噪声等值线，并分析其噪声影响是否相似。设计的3组实验均采用国内某大型枢纽机场2013年的航迹数据，选取某一跑道一天的离港航迹数据进行实验。为确保三维航迹的长度基本相同，以跑道中心为球心，截取空间航迹点到球心距离小于65km 的航迹数据。通过数据预处理，共获取372条标准离港航迹数据。

实验1：三维航迹与航迹速度加权聚类并选取合适的聚类簇数目。采用加权K－medoids航迹聚类算法，求其在不同的航迹聚类个数γ∈［2～］下的DB指标［11］、Dunn指标［12］值 （如图4所示）。

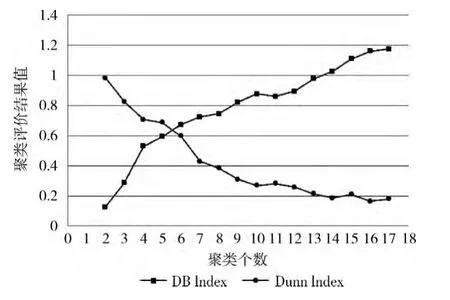
图4 航迹聚类评价结果

DB指标越小、Dunn指标越大，聚类效果越好。由图3可知，当γ为2～9时聚类评价指标浮动比较大，聚类结果不稳定；当γ为10～12时指标比较稳定；当γ为13～17时聚类效果变得越来越差。因此，当γ 为11 时聚类效果最好，航迹聚类为11簇的结果 （如图5所示）。

图5 （a）是11 簇的航迹展示结果，图5 （b）～图5（l）分别表示单独一簇的结果，每一航迹簇的结果在空间上都是独立的，能够很好地对航迹进行划分。

实验2：选取现有的常用飞机发动机推力数据对机型聚类。现有的ANP数据库中有常用的117种机型参数数据，使用k－means聚类算法，聚类数目分别选择选取2～并计算簇内平方误差和对该簇数目下的聚类结果评价，其值越小表明同一簇实例之间的距离越小，聚类效果越好（如图6所示）。由图6可知当聚类个数为9时聚类效果最好，以此，把117种机型聚成9类 （见表4），使机型分类结果更加精细。

选取实验1中的航迹聚类簇再根据机型聚类结果进一步划分。以此，可得到航迹、飞行速度、机型都相似的航迹簇。

实验3：将获取的航迹、飞行速度、机型都相似的航迹簇导入INM 绘制每条航迹的噪声等值线并评估其噪声影响面积、计算其对噪声监测点的噪声值EPNL［13］（单航班事件有效感觉噪声级评价单航班下的航迹对噪声监测点的平均噪声影响值）。由于航迹簇内数据较多，将每一簇中所有航迹全部导入INM 比较困难，因此，选取图5 （b）中航迹簇内具有代表性的6条航迹 （见表5）。编号为a、b、c的航迹的机型A321、B738、B737同属于表4中的Cluster2，编号为d、e、f的航迹的机型同为B772属于表4中的Cluster7。将6条航迹分别导入INM 绘制噪声等直线（如图7所示）。

由图7可以得出在同一航迹簇内，a、b、c在机型相似的情况下3条航迹的噪声等值线相似，d、e、f在机型一样的情况下3条航迹的噪声等值线相似。实验表明在航迹与航迹速度相似的情况下同一机型或者同一类机型下的航迹噪声等值线相似。

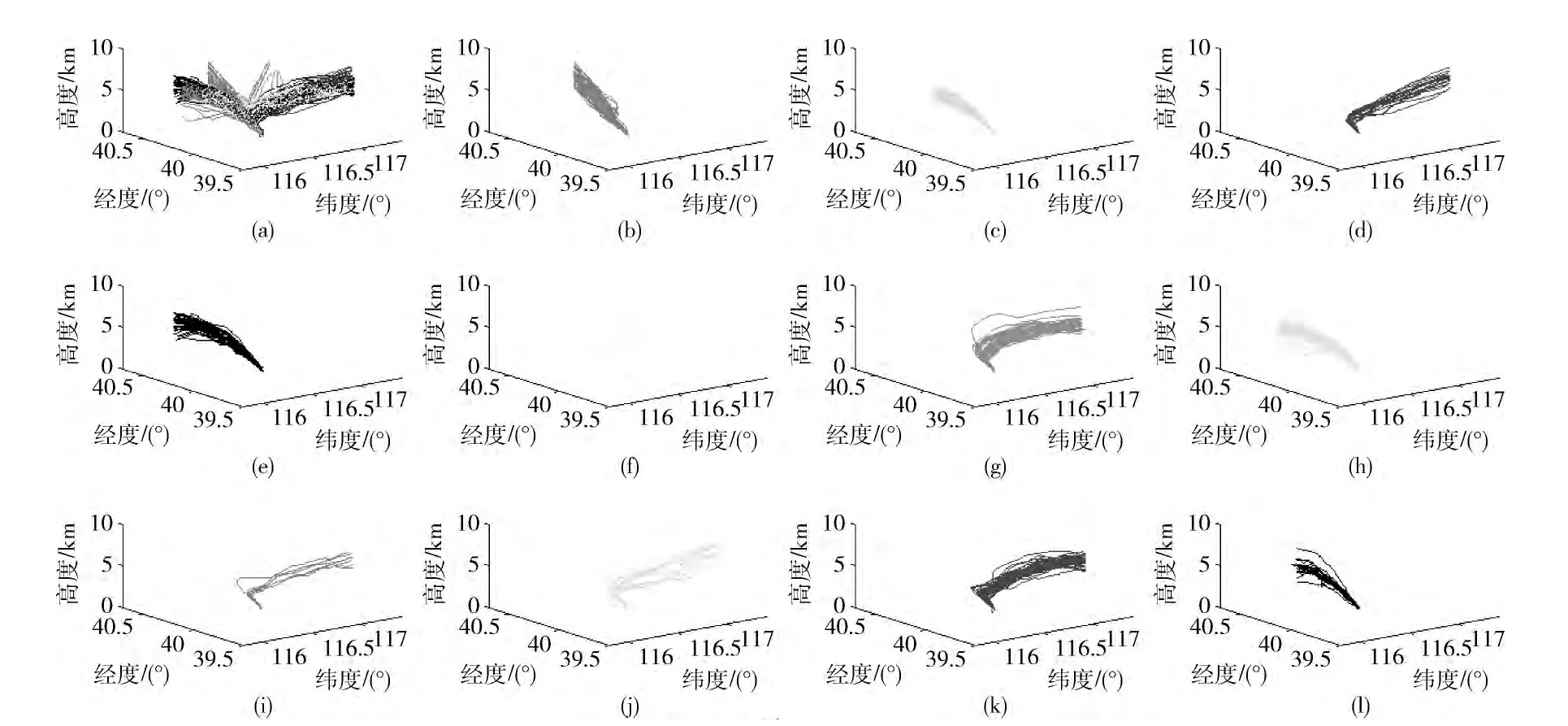
图5 航迹三维聚类结果

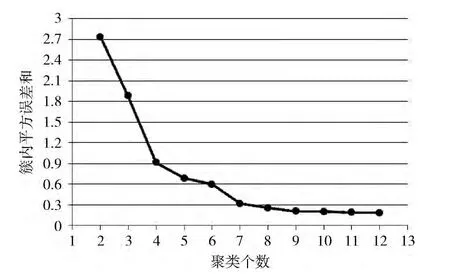
图6 机型聚类评价结果

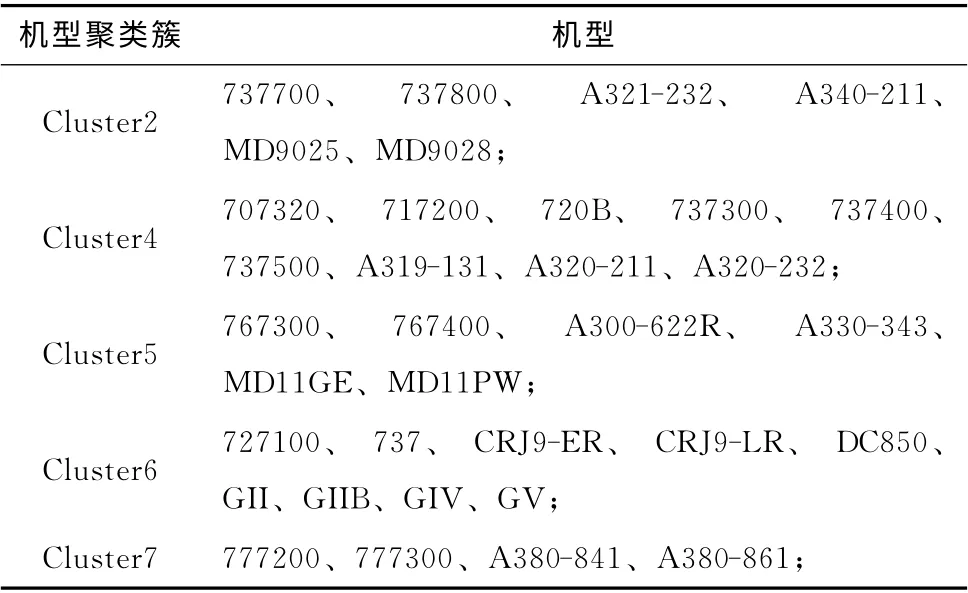
表4 部分机型聚类结果

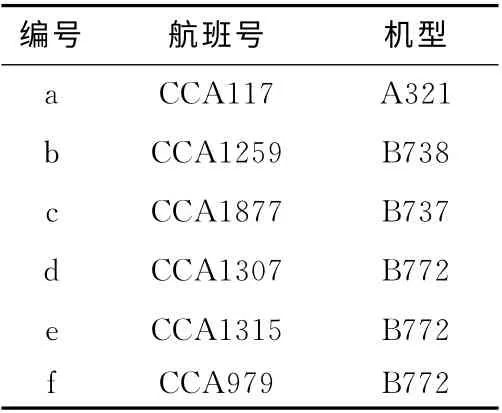
表5 航迹簇数据

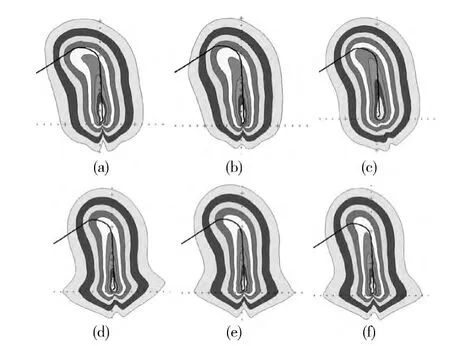
图7 单航迹噪声等值线

采用INM 计算不同噪声等级下每条航迹影响的噪声面积，噪声值从50db～90db每隔5db一个噪声等级，每条航迹对应的噪声影响面积 （如图8所示）。并根据国内某机场实际噪声监测点布局情况，选取17个机场真实噪声监测点模拟导入INM，并计算每一条航迹影响的17个噪声监测值的EPNL （如图9所示）。

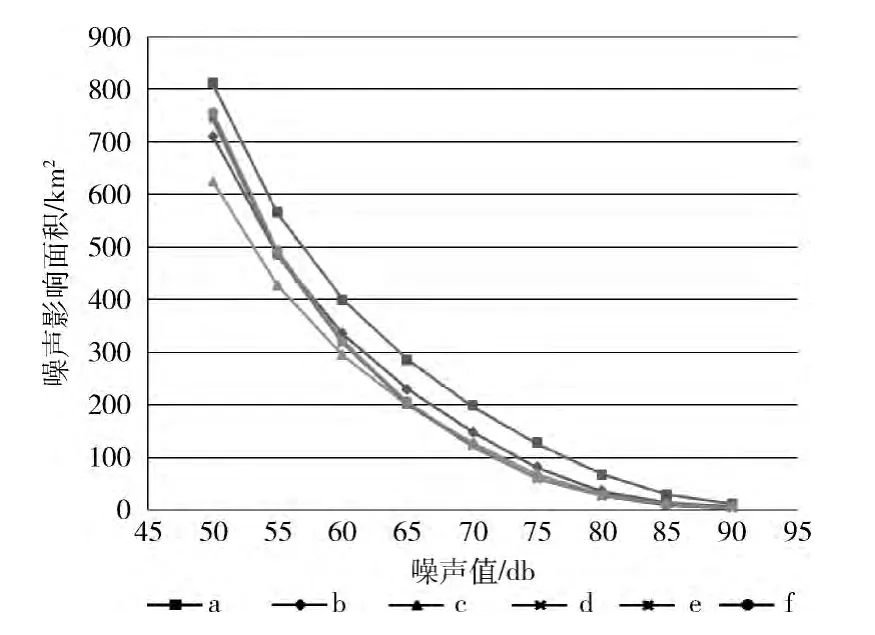
图8 单航迹下的噪声影响面积

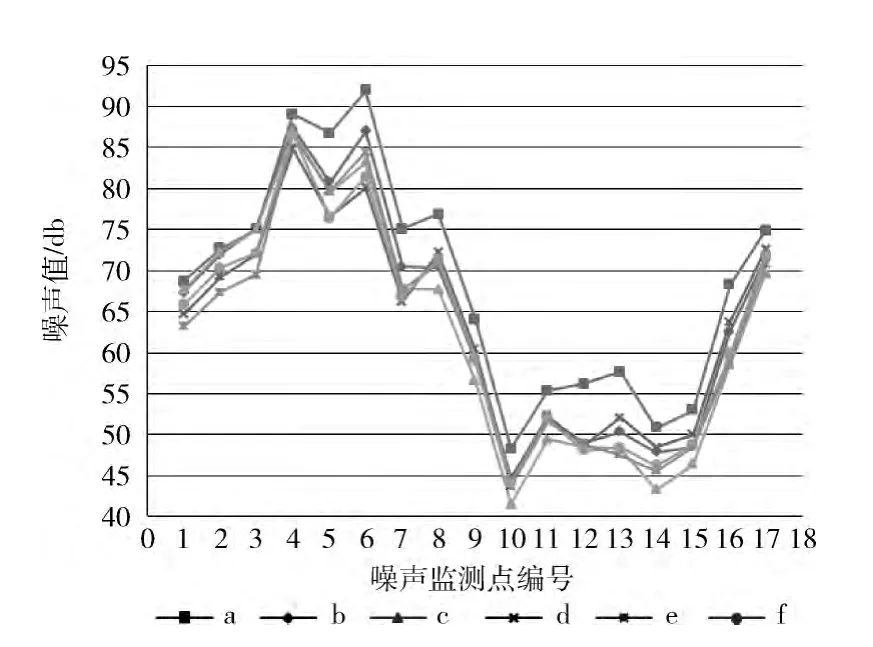
图9 单航迹对监测点噪声监测值的影响

由图8、图9可知a、b、c、d、e、f这6条航迹对应的噪声影响面积和噪声监测值曲线波形相似、波动范围较小，其对噪声的影响非常相似。其中机型一样的情况下，d、e、f这3条航迹对应的噪声影响面积和噪声监测值曲线基本重合。结合航迹和航迹速度的聚类结果再按机型聚类结果进一步划分，能够使航迹簇内的航迹对噪声的影响更加相似。上述实验验证了面向机场噪声预测的航迹聚类模型的合理性和正确性，为机场噪声预测提供更好的理论技术支持。

4 结束语

在分析航迹数据特征的基础上提出了一种基于航迹间面积航迹相似性度量方法，并结合航迹与其速度加权得到航迹的初步聚类结果。对现有飞机机型发动机推力聚类，航迹聚类结果再按照机型聚类结果细划分，使同一航迹簇下再根据机型分类使得航迹聚类结果对噪声的影响范围和噪声影响大小更加相似，把聚类结果导入到INM 输出噪声等值线、不同噪声等级下的噪声影响面积以及模拟真实噪声监测点下的噪声EPNL 值。综合分析结果表明，每一簇的噪声等值线非常相似，验证了模型的合理性，很好地研究了航迹聚类在机场噪声预测上的应用。

［1］Frank R.Clustering of flight tracks ［J］.Proceedings of the American Institute of Aeronautics and Astronautics，2010，34（12）：1－9.

［2］Gariel M，Srivastava A N，Feron E.Trajectory clustering and an application to airspace monitoring ［J］.IEEE Transactions on Intelligent Transportation Systems，2011，12 （4）：1511－1524.

［3］WANG Chao，XU Xiaohao，WANG Fei.ATC serviceability analysis of terminal arrival procedures using trajectory clustering［J］.Journal of Nanjing University of Aeronautics ＆Astronautics，2013，45 （1）：130－139 （in Chinese）. ［王超，徐肖豪，王飞.基于航迹聚类的终端区进场程序管制适用性分析 ［J］.南京航空航天大学学报，2013，45 （1）：130－139.］

［4］WANG Jiening，SUN He，ZHAO Yuandi.Approach trajectory clustering analysis based on time－space ［J］.Science Technology and Engineering，2013，13 （33）：78－81 （in Chinese）.［王洁宁，孙禾，赵元棣.基于时间－空间的进场航迹聚类分析［J］.科学技术与工程，2013，13 （33）：78－81.］

［5］Ministry of Environment Protection.Technical guidelines for noise impact assessment ［S］.Beijing：China Environmental Science Press，2009 （in Chinese）.［国家环境保护局.环境影响评价技术导则：声环境 ［S］.北京：中国环境科学出版社，2009.］

［6］Pardeshi B，Toshniwal D.Improved K－medoids clustering based on cluster validity index and object density ［C］／／Proceedings of the 2nd IEEE International Advance Computing Conference，2010：379－384.

［7］Cao F，Liang J，Li D，et al.A weighting k－modes algorithm for subspace clustering of categorical data ［J］.Neurocomputing，2013，10 （8）：23－30.

［8］Xu J L，Xu B W，Zhang W F.Stable initialization scheme for K－means clustering ［J］.Wuhan University Journal of Natural Sciences，2009，14 （1）：24－28.

［9］Bai L，Liang J.The K－modes type clustering plus between cluster information for categorical data ［J］.Neurocomputing，2014，13 （3）：111－121.

［10］Polczynski M，Polczynski M.Using the K－means clustering algorithm to classify features for choropleth maps ［J］.The International Journal for Geographic Information and Geovisualization，2014，49 （1）：69－75.

［11］Lee S S，Lin J C.An accelerated K－means clustering algorithm using selection and erasure rules［J］.Journal of Zhejiang University（Computers ＆Electronics），2012，13 （10）：761－768.

［12］Zalik K R，Zalik B.Validity index for clusters of different sizes and densities［J］.Pattern Recognition Letters，2011，32（2）：221－234.

［13］Ministry of Environment Protection.GB9660－88standard of aircraft noise environment around airport［S］.Beijing：China Environmental Science Press，1988 （in Chinese）.［国家环境保护局.GB／T9660－1988 机场周围飞机噪声环境标准 ［S］.北京：中国环境科学出版社，1988.］