粗砂细砂复配调整细度模数的研究

杨强，田峻源

（湖南中建五局混凝土有限公司，湖南　长沙　410000）

粗砂细砂复配调整细度模数的研究

杨强，田峻源

（湖南中建五局混凝土有限公司，湖南长沙410000）

本文以粗砂和细砂进行复配，推导出复配后细度模数的简易计算公式及适用范围，并通过混合砂复配试验对公式进行了验证和误差分析。结果表明，选用 4.75mm 筛余小于 50g 的砂复配误差较小；但随着 4.75mm 筛余增加，误差也逐渐增加，且复配比例 1∶1 时，误差最大。

混合砂；复配公式；细度模数

0　前言

随着国民经济的发展，我国的土建事业正在高速发展[1]，混凝土搅拌站也如雨后春笋般不断涌现，各家公司正进行惨烈的竞争。原材料特别是砂的需求量与日俱增，天然砂的开采量巨大，不少地区的天然砂资源已近枯竭，从而导致供应出现前所未有的危机，特别对中砂的需求与日俱增，导致中砂供应极其紧张，经常出现供货商以次充好，以细代粗的情况。然而短时间内试图从源头上解决砂石供应难的问题显然是不可能，也是不现实的。对于出现的细砂，常规的处理方法为与搅拌站库存的中砂或粗砂进行复配，但复配的细度模数调整往往需要进行很多次，基本做法就是传统的细度模数实验法，从而使试验工作量加大，时间拖长，如何简约地计算和调整混合砂的细度模数是一个急需解决的问题[2]。国内许多学者对砂的复配进行了一定的研究，如徐宝华[3]将铁尾矿粗砂与细砂复配，可完全取代天然砂配置混凝土，且性能优于天然砂混凝土；牛威[4]通过对不同细度模数的砂进行混合，用三种不同计算方法进行计算，并检验其误差和带来的影响；孙志刚[5]则对砂细度模数计算方法进行了改进，便于工程人员快速精确计算出结果。其中只有牛威提出了混合砂的细度模数计算公式，但未对公式来源进行标注，也没有对公式进行推导和给出相应的限定条件，可能会造成较大的误差。

本文通过对混合砂复配后的细度模数进行计算，并在限定条件下，推导出简易计算公式，并验证其准确性，为混合砂的复配提供有利的理论依据，降低工作量，加快工作效率。

1　试验

1.1试验用原材料

天然河砂：柒家湖砂场生产的细、中、粗砂

1.2试验仪器

9.50mm、4.75mm、2.36mm、1.18mm、600μm、300μm、150μm方孔筛，并附有筛盖和筛底；天平：称量1000g、感量 1g；摇筛机；烘箱；毛刷等。

1.3试样制备

试验采用细、中、粗砂三种砂，通过细砂与中砂、细砂与粗砂两种混合方式对砂进行混合，验证复配公式与实际配合的差异。三种砂的筛分结果如表 1 所示。

试样的筛分：参照 GB/T 14684－2011《建设用砂》的进行。

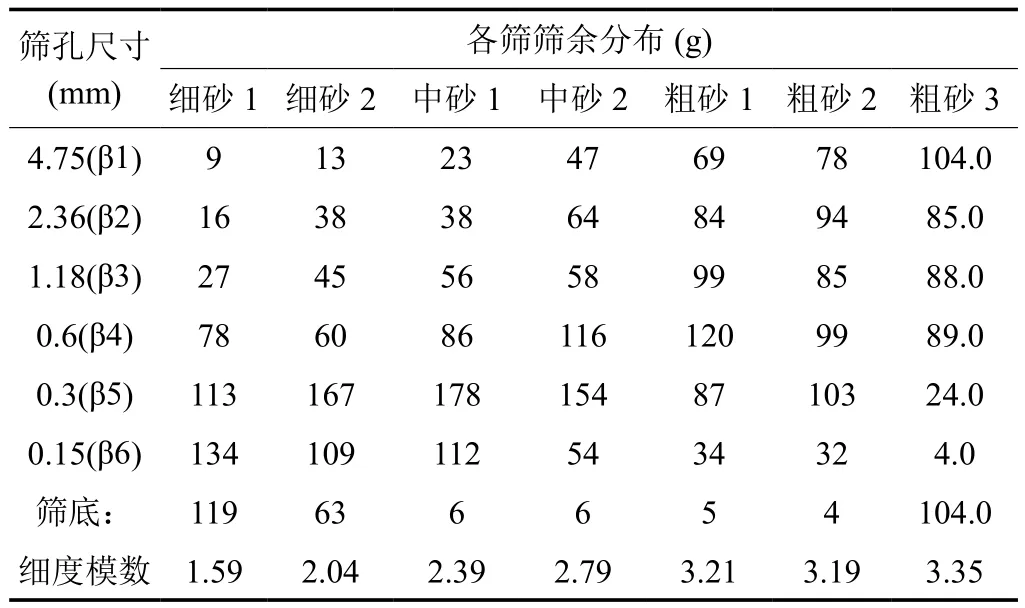
表1　砂的筛分结果

2　混合砂复配公式的推导

设细砂占 x 份，M1为细砂的细度模数，ma1，ma2，ma3，ma4，ma5，ma6分别为 4.75mm、2.36mm、1.18mm、0.6mm、0.3mm 和 0.15mm 筛余量（g）；粗砂占 y 份，M2为粗砂的细度模数，mb1，mb2，mb3，mb4，mb5，mb6分别为 4.75mm、2.36mm、1.18mm、0.6mm、0.3mm 和 0.15mm 筛余量(g)，M3为所配得砂的细度模数，则有：

同理，

由上式可见所配砂细度模数不但与选用两种砂的比例，细度模数有关，还和两种砂 4.75mm 分记筛余量有关，而根据 GB/T 14684－2011《建筑用砂》，合格建筑用砂的 4.75mm分计筛余应在 0%～10% 之间，即 0＜a1＜50，0＜b1＜50，且易知x+y=1，0＜x＜1，0＜y＜1，带入 A 得

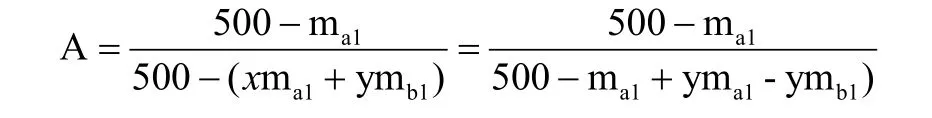
当 0＜a1＜b1＜50 时，

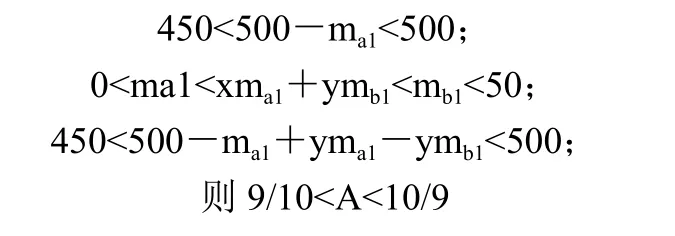
同理，

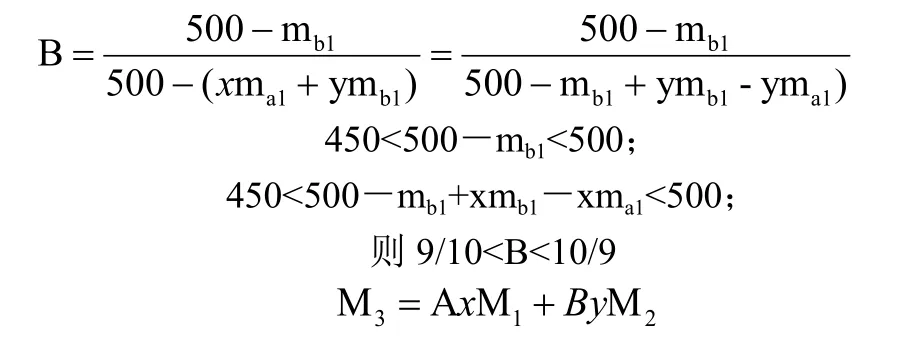
其中当0＜ma1＜mb1＜50时，9/10＜A＜10/9，9/10＜B＜10/9；同理，当0＜mb1＜ma1＜50时，9/10＜A＜10/9，9/10＜B＜10/9，当 ma1=mb1时，A=B=1

综上，A≈1，B≈1

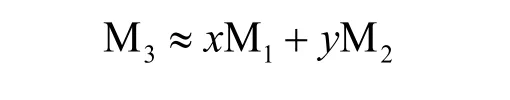
3　混合砂复配公式的评价

为验证上节公式，本节选取细度模数为 1.59、2.04、2.39、2.79、3.19 五种不同河砂，通过对上述砂两两复配对公式进行验证，再以 1.59 与 3.21、3.35 两种 4.75mm 筛余大于 50g 的粗砂进行复配验证该公式的限定条件。以 7 种河砂进行复配，通过筛分得到实际细度模数 M3(实) 与利用公式M3=xM1+yM2得出 M3的比较结果如下表。

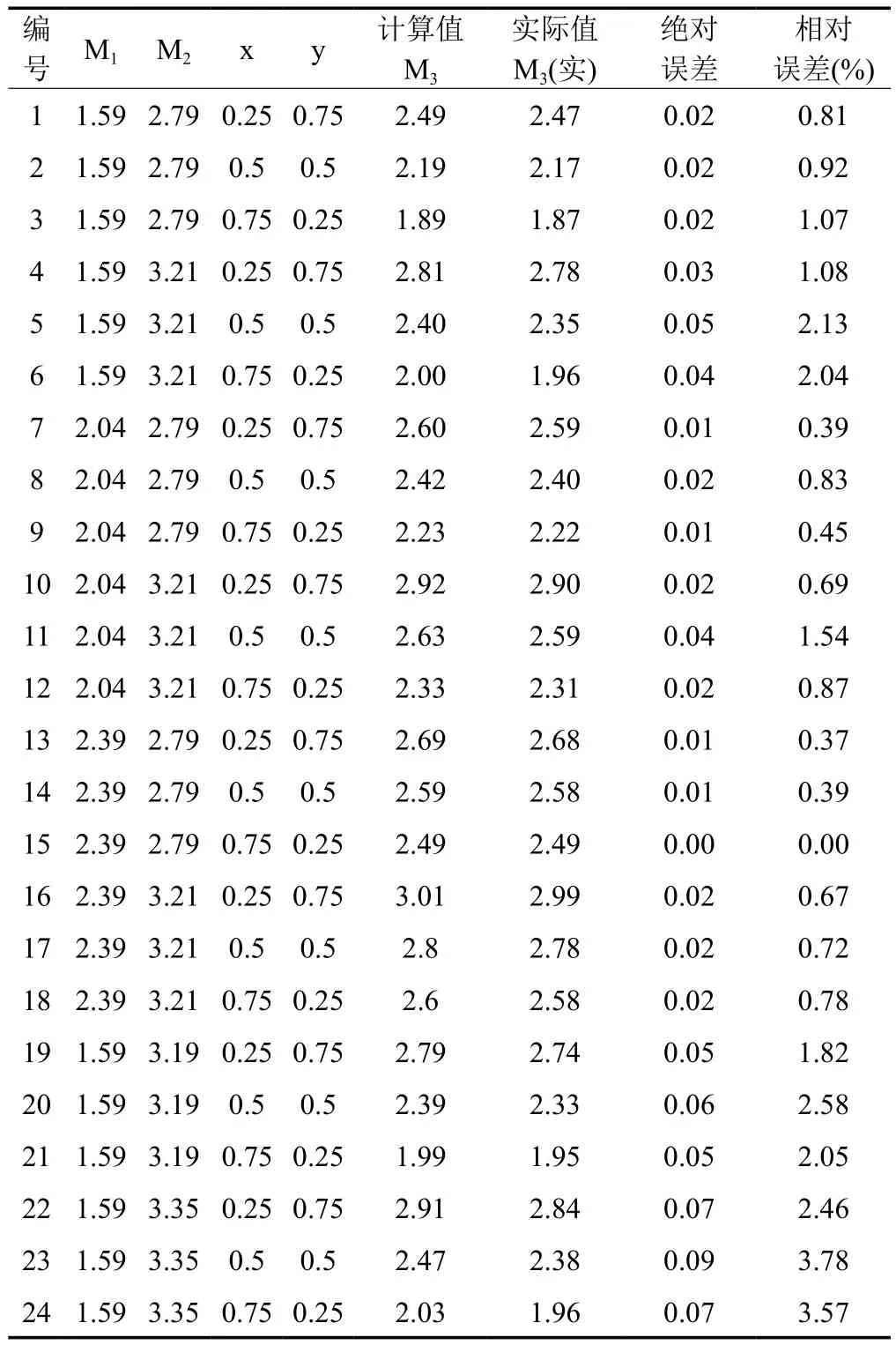
表2　细度模数 M3与 M3(实) 比较结果

由表 2 知，利用公式 M3=xM1+yM2得出的 M3与通过筛分试验测得的 M3(实) 的绝对误差小于等于 0.05，相对误差均小于 2.2%，说明该公式可以用于不同细度模数砂的复配。从表中还可得知，当复配采用 2.79 细度砂时，9 组样品绝对误差小于 0.02，相对误差最高为 1.07%，复配公式能较准确预算复配砂的实际细度模数。而当采用 3.21、3.19、3.35 细度砂时，样品绝对误差在 0.02～0.09 之间，相对误差也有较明显提升，如样品 24 中 1.59 砂与 3.35 砂按 1∶1 复配时，绝对误差达到 0.09，相对误差达到 3.78%，原因是采用的 3.35 砂的4.75mm 筛余远超过复配公式适用的 50g。由表中 1.59 与3.21、3.19、3.35 复配可发现，随着 4.75mm 筛余增多，复配公式的误差也会随之增加，且当复配比例为 1∶1 时，误差较大。但由于砂并非如液体一样属于匀质体，混合后，砂的级配更加完整，往往能使混凝土的性能更优异，故混凝土生产过程中，因粗砂 4.75mm 筛余超过 50g 造成的偏差对生产并不构成直接影响。

4　结论与建议

（1）由推导得出的复配公式 M3=xM1+yM2可用于混合砂的复配中，经过多种细度砂的混合筛分试验对结果进行了验证，证明了复配公式的可行性；

（2）当选用粗砂的 4.75mm 筛余大于 50g 时，复配公式出现一定偏差，随着该层筛余量增多，偏差逐渐增大，且当复配比例为 1∶1 时，偏差较大；

（3）建议进行混合砂复配时，尽量避免选取 4.75mm 筛余过高的粗砂与细砂进行 1∶1 复合，但若将复配公式应用于混凝土搅拌站的生产，该误差对混凝土的生产影响可忽略不计；

（4）建议搅拌站针对不同细度砂进行分仓堆放（尤其以细砂为主），分细度上料，并参照该复配公式对两个砂仓下料比例进行确定，使生产用砂保持在一个较稳定的区间。

[1] 王陆陆．特细砂混凝土性能的试验研究[D]．河北工程大学， 2013．

[2] 孟繁义，陈凤振．机制砂混凝土在南水北调东线穿黄河工程中的应用[J]．中国农村水利水电，2009 (10)： 96-98．

[3] 徐宝华，宋姗．尾矿砂复配在混凝土生产中的研究及应用[J]．商品混凝土，2010(1)：23-25．

[4] 牛威，陈家珑，戴德忠．混合砂细度模数计算方法的研究[J]．混凝土世界，2010 (8)：54-56．

[5] 孙志刚，卢继高，张杰，等．普通混凝土用砂细度模数计算公式的改进建议[J]．中国水泥, 2003 (10)：71-73．

［通讯地址］湖南省长沙市雨花区韶山南路 148号（361027）

The research of the fineness modulus of the mixed sand

Yang qiang, Tian Junyuan
(China construction fifth engineering division concrete Co.,Ltd., Changsha410000)

With coarse sand and fine sand mixed, the simple formulas of complex fineness modulus and its scope was derived. The formulas were validated through trials and error analysis. The results show that the error was small when the sand of 4.75mm sieve was less than 50g.However the error was increasing when sieve residue increases, and the biggest error showed when the complex ratio was 1∶1.

mixed sand; formulas of complex; fineness modulus

杨强，男，工程师。