合金纳米粒子生长形态的分子动力学模拟
余艺, 程庆军, 郭诗奇, 杨剑瑜
合金纳米粒子生长形态的分子动力学模拟
余艺, 程庆军, 郭诗奇, 杨剑瑜
(湖南工程学院理学院, 湖南湘潭, 411104)
选用Cu–Ag纳米粒子作为研究对象, 采用分子动力学方法和嵌入原子模型模拟了将Cu原子注入到由Ag原子构成的纳米粒子的过程, 研究了注入能量(10, 30, 50 eV)与纳米粒子结构的关系。采用共近邻分析技术对合金纳米的结构演变进行了研究。模拟结果表明: 当入射原子动能为50 eV时, 合金纳米粒子从截角八面体转变为二十面体结构。这种转变是因为入射原子与基底原子碰撞, 促使系统温度升高。
Cu–Ag合金纳米粒子; 分子动力学; 近邻分析技术; 截角八面体; 二十面体
纳米合金是由2种以上纳米粒子构成的金属[1–2], 因其独特的物理、化学性质, 在材料科学中有着重要的地位及广泛的应用。纳米合金的性质与其结构(包括构型、尺寸、金属组元及分布、成分比例等)有密切关系。根据应用需要调控其结构是纳米合金制备技术发展的方向。实验制备纳米合金, 一般是让其在一定基底上生长成形, 其结构随生长条件(温度、压强、组元成分比例、基底构型与尺寸等)的变化而演变[3]。如何实现生长条件可控、协调变化, 进而对纳米合金结构进行调控, 是有重要理论价值与实践意义的课题。合金纳米粒子的结构源于形成合金纳米粒子的组元表面能、原子半径的相对大小、合金形成能力的强弱、环境温度、粒子尺寸与合金成分比例等多种因素。目前国内外的研究几乎都是从静态角度, 利用能量优化的方法研究合金纳米粒子的结构。Ferrando课题组应用这一方法研究了同为面心立方结构的2种金属组成的合金纳米粒子结构[4–6], 发现由于表面聚集, 这些合金纳米粒子都有形成核壳结构的趋势, 但其具体构型与粒子尺寸、成分比例有密切关系; Aguado课题组研究了2种体心立方结构的金属元素组成的合金纳米粒子的结构, 发现尺寸较小时, 合金纳米粒子不是核壳结构, 而是与纯元素纳米粒子相似的多面体结构[7]。如上所述, 实验与理论都表明, 合金纳米粒子制备过程中, 其结构与吸附原子在纳米粒子表面的扩散与生长行为有密切联系。在原子尺度上对其结构演变、生长过程进行研究有助于理解其性质, 并达到人为控制其生长形态的目的。这些研究结果说明, 合金纳米粒子结构与合金成分比例、组元与温度等有密切关系。虽然能量优化的方法被广泛应用, 但这种方法有2个缺陷: 第一, 能量局部最小的数量随纳米粒子包含原子数的增加呈指数递增, 因此要找出全局最小需要极大的计算量, 这就使得此方法只适用于小尺度系统[6]; 第二, 合金纳米粒子制备是一个动力学过程, 制备条件对纳米粒子结构影响非常大, 能量最小对应的合金纳米粒子结构仅是理想组态, 因此用能量最优化方法得到的合金纳米粒子结构与实验结果有较大差别。由于实验只是调节某一个生长条件, 也没有考虑到制备过程中生长条件是动态变化的, 这些实验也就不能实现生长条件的可控、协调变化, 而且生长条件影响纳米合金结构的物理机制也还有待深入研究。因此, 已有实验还只是一些零星的、非系统性的研究结果[3, 8–9]。理论研究方面, 分子动力学能跟踪原子运动轨迹[10–12], 已经被广泛应用于研究合金纳米粒子的生长形态。为研究Cu–Ag合金纳米粒子生长形态的调控和合金纳米粒子结构随温度、尺寸、合金成份比例与组元结构等生长条件的变化规律, 将Cu沉积原子注入到Ag原子纳米尺度的基底中, 基底的动能设置为0, 用高能粒子(Cu原子)的碰撞使基底转变生长方式。为实现这一目标, 本文从理论上阐明影响合金纳米粒子结构的因素及演变规律,着重探讨注入能量这一因素对截角八面体结构的201个Ag原子生长形态的影响。
1 模型与方法
利用分子动力学进行计算机模拟时, 准确描述原子间作用力势函数是模拟成功与否的关键[12–14]。嵌入原子方法(EAM)能够很好地描述金属原子间多体相互作用。表面能和晶格常数2个物理量是纳米粒子生长模拟的重要因素, 其中晶格常数的实验值被作为输入参数来确定EAM模型参数。因此, 应用EAM模型计算了2个元素的表面能()可以验证模型的正确性。在一般情况下, 表面能随着表面原子的配位数减少而相应减少, 因此对于面心立方结构的金属, 其表面能的顺序应该是110>100>111(表1)。EAM模型准确地预测了表面能的这一趋势, 计算结果与实验结果和第一原理结果也比较接近。因此, 本模型能准确描述Cu–Ag纳米粒子。

表1 利用第一原理(FP)与嵌入原子方法(EAM)计算的Cu和Ag表面能及其实验值(Exp) /( mJ·m-2)
研究发现[1–2], 对于面心立方结构(FCC)金属, 截角八面体(TO)与二十面体(ICO)结构的纳米粒子是最稳定的结构。因此, 选择201个原子的截角八面体(TO201)和147个原子的二十面体(ICO147)作为研究对象, 这2种纳米粒子的构型如图1所示。截角八面体由8个{111}晶面和6个{100}晶面构成, 需要指出的是{111}与{100}面是面心立方结构的密排面, 也是最稳定的表面, 截角八面体构型与球形比较接近, 这也使得它的结构更为稳定。二十面体则是以2个五角形金字塔为基础, 它的表面只有排列最为紧密的{111}晶面, 从这点来说, 它也是一种稳定结构。另外, 为便于说明这2种纳米粒子的结构特点, 分别在TO201与ICO147纳米粒子表面上描绘出一个正六边形与正五边形, 如图1中的白色多边形所示。

图1 201个原子的截角八面体和147个原子的二十面体结构
在生长模拟中, 利用分子动力学方法模拟将具有一定动能的Cu原子沉积到截角八面体的Ag纳米粒子上, 沉积原子的能量范围是10~50 eV。本文以注入能量为10, 30, 50 eV为例来说明模拟结构。生长模拟在等容等能(NVE)与等容等温(NVT)的正则系统中进行。首先在NVE系统中, 模拟具有一定动能的Cu原子的注入沉积过程, 经过0.3 ns的模拟, 系统基本达到平衡状态。然后经过2.7 ns的NVT系统模拟, 将系统平衡在温度为100 K的状态。最后记录所有原子的位置和速度, 以便于做结构和动力学特性分析。在分子动力学模拟中, 利用预测–校正算法求解原子的牛顿运动方程, 时间步长取2.0 fs。为保证系统的动量为0, 3个Cu原子被均等地沉积到Ag基底上, 其中每个Cu原子的运动方向都指向Ag纳米粒子中心。
如图2所示, 当入射的Cu原子动能为50 eV时, 在开始阶段(NVE系统), 系统温度(约800 K)远高于设定的温度(100 K), 这是因为Ag基底原子获得了入射Cu原子的动能。然后在NVT系统下, Cu–Ag系统温度逐渐降低, 最后平衡在设定的100 K左右。所有物理量都在100 K下统计获得。

图2 Cu原子入射能量为50 eV时基底纳米粒子温度随时间变化
2 结果与讨论
当把Cu原子注入到Ag纳米粒子TO201, 纳米合金首先在NVE中模拟沉积过程(见图2), 入射能量等于50 eV时, Cu原子的入射能量传递到基底, 基底原子之间剧烈碰撞, 使系统温度变为约850 K。NVE中模拟的850 K高温会导致Ag纳米粒子基底开始快速扭曲变形, 然后经过2.7 ns的NVT模拟, 系统平衡温度冷却至100 K, 纳米粒子由高温(850 K)时的液态凝固成一定结构的固态。通常的分析技术, 如径向分布函数和静态结构因子, 只能从整体上对结构作有序与无序的判断。为更细致地研究纳米合金的结构变化过程, 采用共近邻分析技术(CNA)确定凝固的Cu–Ag合金纳米粒子结构。共近邻分析技术通过3位数(,,)描述原子所属的状态,表示成键的2原子的共有最近邻原子数,表示共有最近邻原子之间的成键数,表示共有最近邻原子所成键链中最长链上的键数。当将Cu原子入射到Ag基底中, 入射能量为10, 30, 50 eV时, 共近邻分析的结果列于表2。
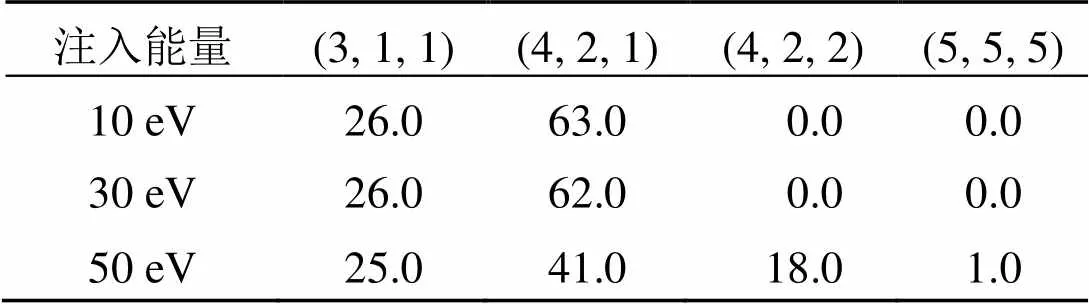
表2 Cu注入到Ag的TO201中(3, 1, 1), (4, 2, 1),(4, 2, 2)和(5, 5, 5)等键对占总键对的百分比 %
根据共近邻分析方法, 每一种键对都对应着特定的原子空间几何构型。其中FCC型晶体中以(4, 2, 1)键为特征键对; HCP型晶体则同时以(4, 2, 1)和(4, 2, 2)为特征键对。(3, 1, 1)是纳米粒子的表面原子, (5, 5, 5)是二十面体5重对称性的晶序特性。因此仅需要(3, 1, 1), (4, 2, 1), (4, 2, 2), (5, 5, 5)这几种晶序就能区分TO201, ICO147结构。
如表2所示, 当Cu原子以10 eV和30 eV的能量入射TO201时, 新的Cu–Ag合金纳米粒子中没有(4, 2, 2)和(5, 5, 5)构型, 仅有(3, 1, 1)与(4, 2, 1)键, 且这2种键型所占百分比与Ag的TO201类似, TO201的Ag基底具有{111}和{100}面, 经CNA分析, (4, 2, 2)和(5, 5, 5)键对数为0。这表明当Cu原子以较低能量入射时, Ag基底仍保持着原来的结构而没有发生变化。当入射的Cu原子动能增加大到50 eV时, (4, 2, 2)键所占百分比提高到了18%, (4, 2, 1)键的比例减少到41%。需要指出的是, 在此情形下, 有少量的(5, 5, 5)键型。这种键型特征与ICO147类似。共近邻分析方法说明, 由于高能量的Cu原子注入, Ag纳米粒子由TO转变为ICO结构。用Cu原子注入后, 合金纳米粒子结构演变过程图更直接地说明这种转变。
如图3所示, 动能为10 eV的Cu原子入射到Ag的TO基底上, Ag基底几乎保持了原来的TO结构, 入射的Cu只是嵌入到Ag基底中。最终平衡后, 合金纳米粒子保持了原来的六边对称性。
当入射的Cu原子动能为50 eV时(图4), 与10 eV相比, 50 eV的Cu原子与基底的Ag原子强烈作用, 粒子的运动过程要更加复杂, 温度急剧升高促使结构发生变化, 由6重对称演变成5重对称。Ag纳米粒子出现了5重对称结构, 并出现了几个{100}面, 这样的结构更类似于ICO构型。另外, 因Ag原子表面能较低、原子半径较大, 最终导致50 eV入射的Cu沉积原子在进入TO后偏析于Ag纳米粒子表面。
如图5所示, 对尺寸较小的Cu纳米粒子, ICO比TO稳定, 因此TO比ICO更容易演变成其它结构。对所有尺寸的Ag纳米粒子, TO比ICO更稳定, 这一结果与其它理论的计算结果一致。当Cu注入到Ag的TO201基底中, 因TO很稳定, 其很难演变成ICO。因此, 只有当以较大动能的Cu原子注入到Ag基底中, 使基底原子发生较大变化, 才能使Ag基底从TO转化为ICO。

图3 注入能量为10 eV的Cu原子沉积到结构为TO的Ag基底中纳米粒子构型演变

图4 注入能量为50 eV的Cu原子沉积到结构为TO的Ag基底中纳米粒子构型演变

图5 (Cu, Ag)TO和ICO结构结合能随原子尺寸的变化
为了解释这一模拟结果, 进行了一系列不同尺寸的TO和ICO纳米粒子的MD模拟实验, 证明每个原子结合能的大小与原子尺寸相关。
3 结论
用分子动力学和原子嵌入模型研究了能量在10~50 eV的Cu原子沉积到TO201构型的Ag纳米粒子基底的过程, 分析了生长出的Cu–Ag纳米合金结构的早期演变过程。应用共近邻分析技术, 发现当入射Cu原子的能量为10 eV和30 eV时, 生长出的纳米合金粒子基本保持了原有TO形态; 在50 eV时, 纳米粒子由六重对称性变为五重对称性。因沉积原子的能量被均匀地分配到基底每个原子, 基底原子不断挤压碰撞导致了系统温度的升高, 温度的升高进而导致了纳米粒子结构的转变。
参考文献:
[1] Baletto F, Ferrando R. Structural properties of nanoclusters: Energetic, thermodynamic, and kinetic effects [J]. Rev Mod Phys, 2005, 77(1): 371–423.
[2] Ferrando R, Jellinek J, Johnston R L. Nanoalloys: from theory to applications of alloy clusters and nanoparticles [J]. Chem Rev, 2008, 108(3): 845–910.
[3] Chaudhuri R G, Paria S. Core/shell nanoparticles: classes, properties, synthesis mechanisms, characterization, and applications [J]. Chem Rev, 2012, 112(4): 2 373–2 433.
[4] Rapallo A, Rossi G, Ferrando R, et al. Global optimization of bimetallic cluster structures. I. Size-mismatched Ag-Cu, Ag-Ni, and Au-Cu systems [J]. J Chem Phys, 2005, 122(19): 194308(1–13).
[5] Rapallo A, Rossi G, Ferrando R, et al. Global optimization of bimetallic cluster structures. II. Size-matched Ag-Pd, Ag-Au, and Pd-Pt systems [J]. J Chem Phys, 2005, 122(19): 194309(1–9).
[6] Negreiros F R, Barcaro G, Kuntova Z. et al. Structures of gas-phase Ag-Pd nanoclusters: A computational study [J]. J Chem Phys, 2010, 132(23): 234703(1–8).
[7] Aguado A, Lopez J M. Structure determination in 55-atom Li-Na and Na-K nanoalloys [J]. J Chem Phys, 2010, 133(9): 094302(1–10).
[8] Serpell C J, Cookson J, Ozkaya D, et al. Core@shell bimetal-lic nanoparticle synthesis via anion coordination [J]. Nat Chem, 2011, 3(6): 478–483.
[9] Radilovic V, Ophus C, Marquis E A, et al. Highly monodisperse core-shell particles created by solid-state reactions [J]. Nat Mater, 2011, 10(9): 710–715.
[10] 文玉华, 朱如曾, 周富信. 分子动力学模拟的主要技术[J]. 力学进展, 2003, 33(1): 67–71.
[11] 蔡锡年. 分子动力学和物理力学[M]. 北京: 科学出版社, 1986: 100–110.
[12] 周健, 陆小华, 王延儒, 等. 分子动力学模拟[J].南京化工大学学报, 1997, 19(2): 20–25.
[13] Vitos L, Ruban A V, Skriver H L. et al. The surface energy of metals [J]. Surf Sci, 1998, 411(1–2): 186–202.
[14] Tyson W R, Miller W A. A Comprehensive Search for Stable Pt-Pd Nanoalloy Configurations and Their Use as Tunable Catalysts [J]. Surf Sci, 1977, 62(1): 267–276.
(责任编校:刘刚毅)
The growth configuration of nanoalloy: a molecular dynamics simulation
Yu Yi, Cheng Qingjun, Guo Shiqi, Yang Jianyu
(Science College, Hunan Institute of Engineering, Xiangtan 411104, China)
The impact depositions of Cu atoms onto the Ag truncated octahedron are simulated by molecular dynamics along with the embedded atom method. The dependence of incident energies (10, 30 and 50 eV) and the nanoalloy configuration is found. The common neighbor analysis is used to identify the structural evolutions. A structural transformation from truncated octahedral to icosahedral arrangement is observed at incident energy of 50 eV. The structural transformation can be induced by the increase of system temperature, because the incident energy of the deposited atom is delivered to the substrate atoms as a result of collisions.
Cu-Ag nanoalloy; molecular dynamics; common neighbor analysis; truncated octahedron; icosahedron
10.3969/j.issn.1672–6146.2015.01.005
O 781
1672–6146(2015)01–0017–04
杨剑瑜, hnieyjy@aliyun.com; 余艺, 1847997096@qq.com。
2014–11–15
国家自然科学基金(50971058), 2014年湖南省大学生科技创新项目。

