几种连续波雷达系统参数设计和信号处理方法
郭 云,余 奎,陈 坚
(江西洪都航空股份有限公司650所,江西南昌 330024)
连续波雷达由于结构简单、体积小、无距离盲区、低功耗和低截获、成本低等优点,在军用导航,战场侦察等领域得到广泛应用。连续波雷达按照发射信号的形式可以分为非调制单频或多频连续波雷达、调频连续波雷达、步进频率连续波雷达等。双频连续波雷达信号处理过程简单,但存在测距最大不模糊距离和测距精度之间不可调和的矛盾[1];多频连续波雷达通过解模糊处理解决了最大不模糊距离和测距精度之间的矛盾[2-3],但其体制决定了其对同速不同距的目标无法分辨;步进频率连续波雷达由一串载频线性跳变的雷达发射信号组成[4],通过对回波的IFFT处理获得距离高分辨率的效果,但其在多目标观测情况下,对各个目标的速度进行精确估计和补偿较为困难,从而无法获得目标真实的位置信息;步进频移键控波形[5]综合了上述3种波形的优点,具有较高的距离和速度分辨率、较短的测量时间并且解决了同速不同距的多目标分辨问题。
本文通过对双频连续波、多频连续波、步进频率连续波和步进频移键控连续波等4种体制连续波雷达信号处理系统的参数设计和信号处理关键问题进行对比分析,得到了各个波形的特点,并通过计算机仿真进行了验证。综合仿真结果和理论分析得到,步进频移键控连续波,能在一个处理周期内对多目标进行分辨。
1 双频连续波雷达信号处理
双频比相测距算法[1-2]同时发射两个点频连续波信号,对接收到的回波信号进行混频、采样等操作,然后进行FFT处理,利用处理后双频信号的相位差Δφ且实际的相位差为对Δφ以2π取模解算后得到的,如果Δφ超过了2π,由此获得的距离为模糊距离为
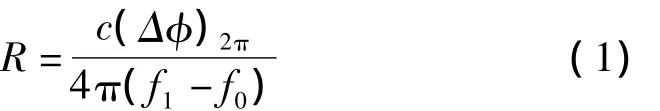
双频比相测距相位测量均方根误差[1]为 1/,双频比相测距算法所能达到的理论测距精度为 c/4πΔf。其中,SNR为比相输出信噪比,为减小距离模糊,必须减小双频频差,但这样又会使测距精度随之降低,所以双频连续波雷达存在着测距最大不模糊距离和测距精度之间不可调和的矛盾。
2 多频连续波雷达信号处理
为解决测距最大不模糊距离和测距精度之间的矛盾,多频连续波雷达被提出,其发射波形如图1所示,先发射双频信号f0和fn+1,然后发射下一组双频f0和fn,…,最后发射双频f0和f1。其处理流程如下[3]:
(1)根据本次测量所要求的最大不模糊距离来确定最小二次频差ΔF=Δfn-Δfn+1的值。
(3)选择 Δf1=f1-f0=N(Δf1-Δf2),即 Δfn-。则。式中,Δf其实是一次1频差,而不是二次频差,它和前边的二次频差Δf1-Δf2也是N倍关系,这样可以提高频率利用率,增大测距精度。
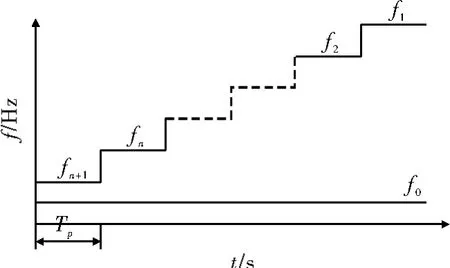
图1 二次相差法发射频率波形图
二次相差
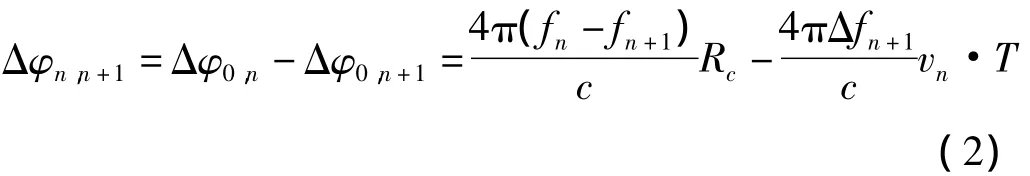
最大不模糊距离为
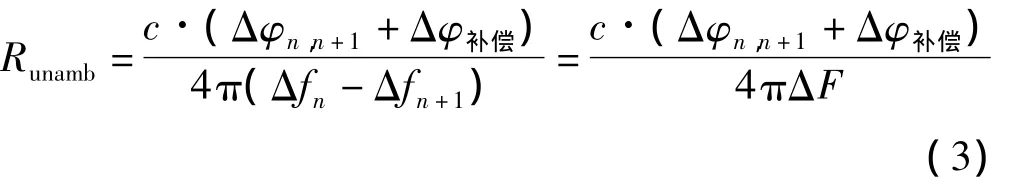
3 步进频率连续波雷达信号处理
步进频率连续波雷达信号[4]是一种大时宽带宽,具有良好的距离和多普勒分辨能力,发射波形如图2所示。
对步进频率连续波雷达的信号处理主要分为3部分[6]:
(1)IFFT处理。假设信号发射频率依次为f0、f1、f2、…、fM-1,且在存在 I个目标,则发射频率为 fm的回波信号经过相干检波后,进行IFFT变换,得到

图2 步进频率连续波雷达发射频率波形图
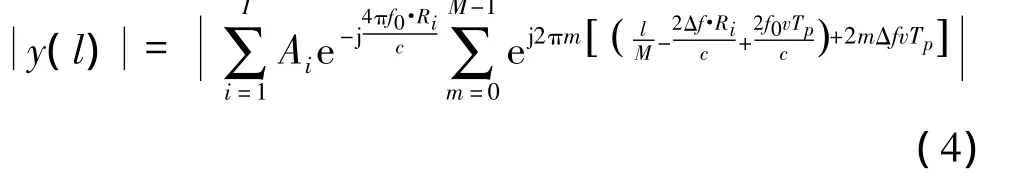
得到距离公式如下
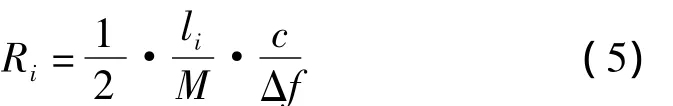
距离分辨力为
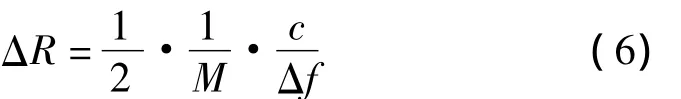
步进频率信号的数据率较低,对于多普勒效应较敏感[7]。在实际应用中应考虑多普勒效应带来的偏差。目标运动给回波造成附加的一次相位项和二次相位项,如式(7)所示

一次相位项在IFFT结果中产生耦合时移,使误差与速度v成正比;二次相位项主要会使IFFT结果能量发散,其程度与v成正比。一次相位项主要造成测距不准,二次相位项则可能产生伪峰和幅度损失,因此需要对目标的多普勒效应进行补偿。
(2)N个周期MTD处理。假设总共发射了N个周期的步进频率连续波信号,设第n个周期步进频率连续波回波信号处理得到的yn(li)为u(n),进行FFT变换得到
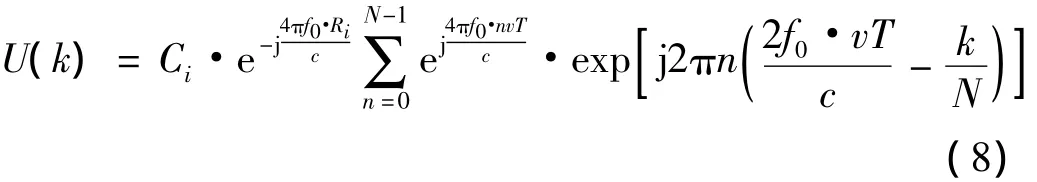
进行谱峰搜索就可以得到目标i的速度估计值

速度分辨率为
由以上分析可知,通过MTD处理可以获得目标的速度,从而获得解耦合后的目标距离。但某些系统参数下的多目标环境下,如远作用距离,快速目标观测,其需要选择合适的Δf从而保证最大的作用距离,对于同样的距离分辨率的情况,这会增大步进的频率点数,增加每一周期的时间,对于快速目标MTD处理可能会出现测速模糊,从而导致距离和速度的测量误差增大。
4 步进频移键控连续波雷达信号处理
由于多频连续波雷达无法解决同速不同距的多目标分辨问题,步进频率连续波雷达需要对目标的多普勒效应进行补偿,因此特提出一种步进频移键控连续波雷达体制,发射波形如图3所示。其发射信号借鉴双频和步进频率连续波雷达的特点,发射A路和B路两路频率步进信号,两路信号的频率步进量和带宽相同[7],同时两路步进频率信号起始频率差为fstep。
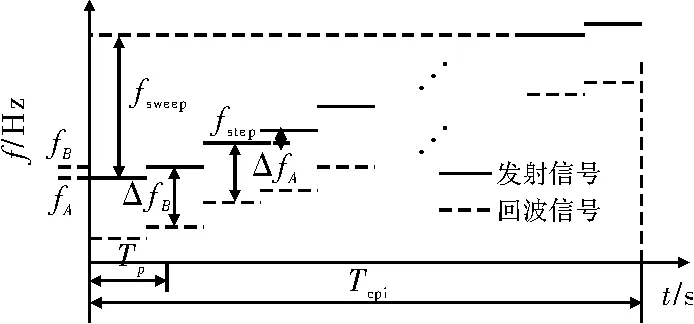
图3 步进频移键控连续波雷达发射波形
对步进频移键控连续波雷达的信号处理流程如下:假设A路步进频率连续波信号发射频率依次为f0、f1、f2、…、fM-1,则发射频率为 fm的回波信号经过相干检波后,取最后一个采样点得进行FFT变换后得到
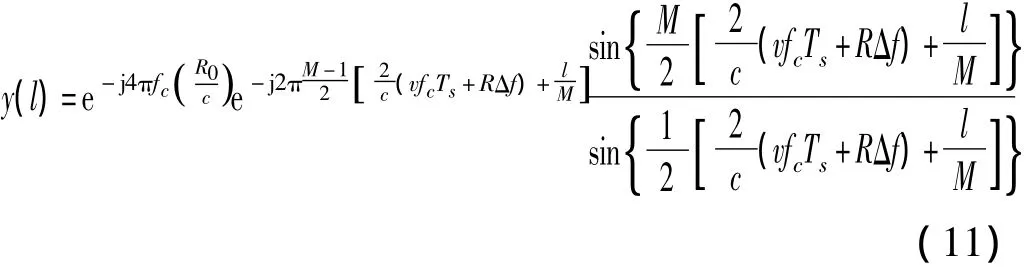
由式(11)可得,FFT处理后的谱峰位置lm为
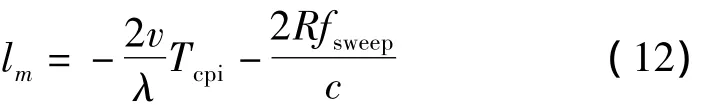
其对应的频率ΔfA为
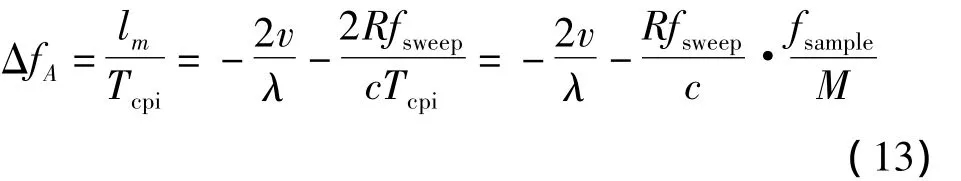

联立式(13)和式(14)求解方程组,可解算出目标的R和v。距离分辨率为速度分辨率为


由上述分析可知,步进频移键控连续波雷达可以在一个相参处理周期内同时获得目标的距离和速度信息。
对于速度变换目标的补充说明:设目标的速度a以加速度变换,为推导方便,设a恒定,之后可由此推及a发生变化的一般情况。由式(11)信号进行FFT变换后,加速度会产生项,需要给式(11)乘以由于本算法参数设置,即对于速度变换目标,由于每个信号频率发射时间较短,速度变换带来的仿真误差可忽略不计,这种情况可适用于速度非线性变换的目标。
5 计算机仿真分析
(1)多频连续波雷达仿真分析。
1)仿真参数。假定基频f0=1.5 GHz,首先根据本次测量所要求的最大不模糊距离来确定最小二次频差ΔF=Δfn-Δfn+1的值。为实现最大不模糊距离 Runamb=30 km,设置最小的二次频差为Δf4-Δf5=5 kHz。为使距离分辨率为30 m,最大的一次频差为f1-f0=6.24 MHz,根据前面的推导,取二次差频增大倍数。发射5组点频的连续波信号,Δf4-Δf5=5 kHz、Δf3-Δf4=30 kHz、Δf2- Δf3=180 kHz、Δf1- Δf2=1.04 MHz、f1- f0=6.24 MHz。因此,f0=1.5 GHz、f1=1.506 24 GHz、f2=1.505 2 GHz、f3=1.505 02 GHz、f4=1.504 99 GHz、f5=1.504 985 GHz。
2)噪声干扰分析。假设目标速度v=70 m/s,目标距离为3 000 m。第一次实验SNR从0~50 dB依次增大,每次增加0.1 dB;第二次实验SNR从 -20~30 dB依次增大,每次增加0.1 dB。100次蒙特卡罗仿真结果如图4和图5所示。
由图4和图5所示,二次相差测距精度受噪声干扰较明显,测距均方根误差随信噪比增大而迅速降低,当信噪比<-5 dB时,测量误差均方根急剧增大。
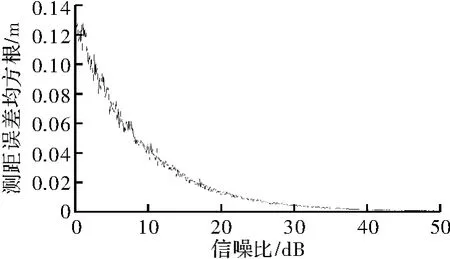
图4 信噪比为0~30 dB时二次相差法测距均方根误差曲线
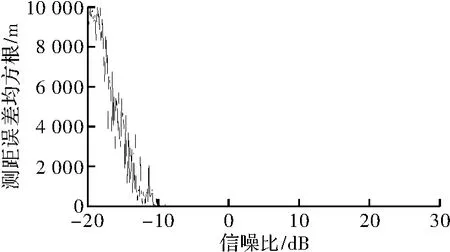
图5 信噪比为-20~30 dB时二次相差法测距均方根误差曲线
3)二次相差法多目标分辨问题仿真分析。图6和图7分别为两个目标同速度和不同速度情况下的FFT幅度谱,可以看到,当两个目标速度相同时,其FFT频谱会重叠在一起,无法通过谱峰搜索的方法来分辨多个目标,因此基于双频比相测距的二次相差测距算法无法分离具有相同速度的多个目标。

图6 同速度的两个目标的FFT谱分析
(2)步进频率连续波雷达仿真。
1)仿真参数。取基频 fc=1.5GHz,由式(5)和式(6)为使单帧最大测距范围为Rmax=30 km,取频率步进Δf=4.8 kHz为使距离分辨力为ΔR=30 m,步进频率个数M=1 024。由式(9)和式(10)得,为使测得的速度多普勒频谱分辨率为0.5 m/s,设每个频率的发射信号持续时间Tp=208μs,一帧M=1 024个步进频率的发射接收周期T为0.213 s。发射步进频率连续波信号帧数N=5,采样频率为fs=5 MHz,每个频率fm采样1 024个点。

图7 不同速度的两个目标FFT谱分析
2)多目标分辨问题仿真分析。设3个目标具有相同速度70 m/s,距离分别3 000 m、2 500 m、2 000 m,图8是距离维IFFT的距离-幅度关系图。求出的距离测量值分别为R1=7 537.8 m、R2=7 049.6 m、R3=6 561.3 m。测量误差分别为4 537.8 m、4 549.6 m、4 561.3 m。
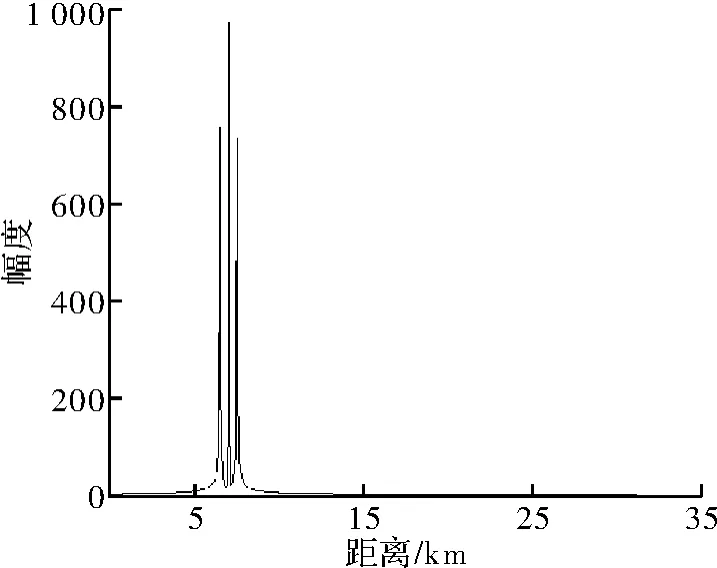
图8 距离维IFFT的距离-幅度关系
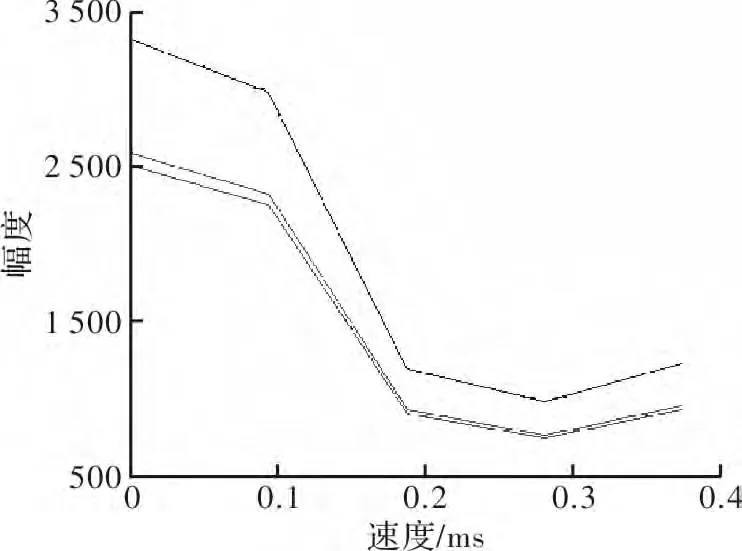
图9 N帧速度维FFT的速度-幅度关系
可以看出距离维IFFT变换能够分辨出3个目标,但偏差较大。第3步N帧FFT变换分辨多普勒频率范围最大为5 Hz,速度分辨率为1 Hz,对于高速目标会产生测速模糊问题。不对目标IFFT变换进行速度补偿,采用步进频率连续波雷达IFFT变换后测得的距离值较正常值偏差较大,>4 500 m,测速的最大多普勒频率为5 Hz,对应最大不模糊速度为0.5 m/s,在现有参数下,无法准确获知目标的运动速度,也就无法准确测得目标的距离。
3)噪声干扰分析。仿真分析步进频率连续波多目标分辨算法的测距误差与FFT输出信噪比之间的关系。这里依然假设目标速度v=70 m/s不变,目标距离为10 000 m不变。实验时SNR从-50~30 dB依次增大,每次增加0.5 dB,并用目标的真实速度进行距离补偿。每次进行100次蒙特卡洛仿真实验。
图10给出了100次仿真实验速度补偿后测距均方根误差与信噪比的关系曲线。从图中可以看出,测距均方根误差随信噪比变化较明显,当信噪比<-25 dB时,测距均方根误差急剧增大。

图10 步进频率连续波雷达速度补偿后测距误差与信噪比的仿真结果
总体来说,步进频率连续波多目标分辨算法与二次相差法测距算法相比,算法复杂度及运算量更大,但测距精度较差,而且步进频率连续波多目标分辨算法能够有效地分辨多个目标,不论它们是同速度还是不同速度。
(3)步进频-键控波形仿真。
1)仿真参数。参数设置列表如下:由式(15)和式(16)可知,类似于步进频率连续波仿真参数设置,为使距离分辨力为ΔR=30 m取fsweep=5 kHz,为使最大测距范围为Rmax=30 km,取步进频率个数 M=1 024。为使速度分辨率为0.3 m/s,Tcpi=0.426 0 s。

表1 步进频-键控波形仿真参数设置
2)单目标仿真分析(信噪比5 dB)。
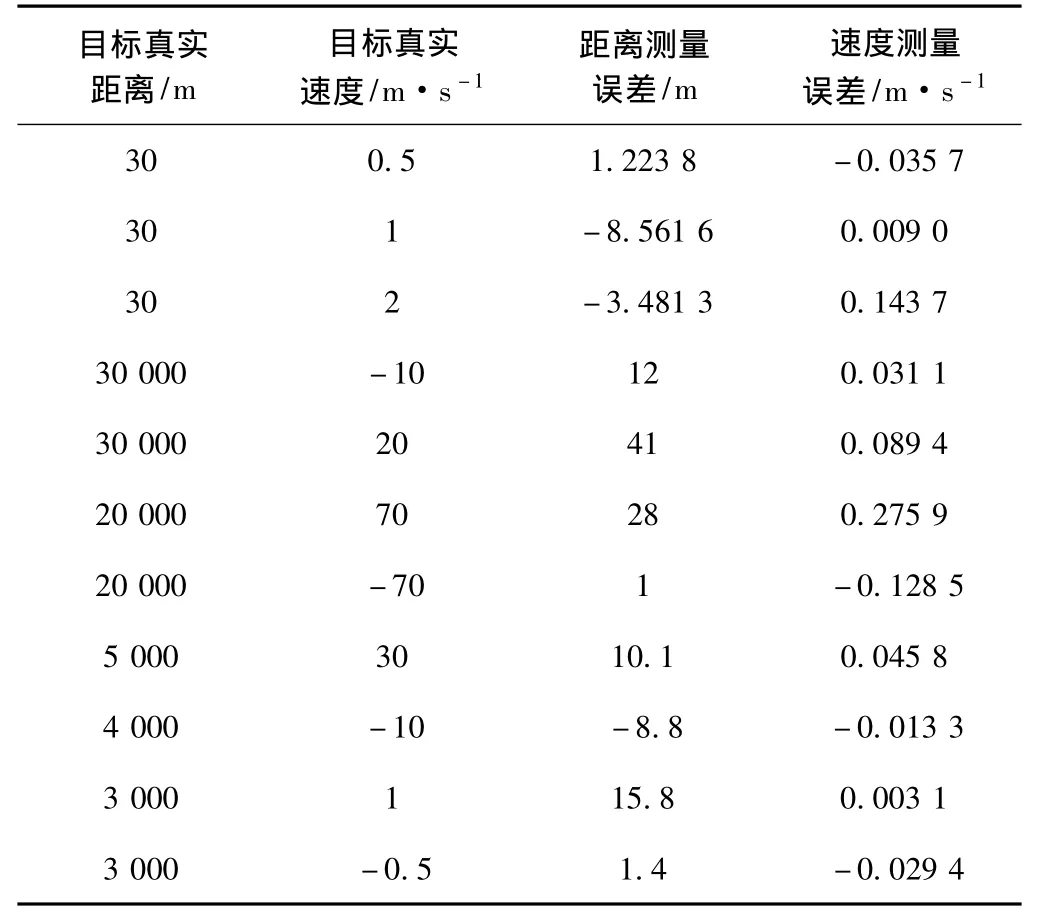
表2 不同速度和距离组合目标测量结果
可以看到在信噪比为5 dB时,步进频移键控波形处理方法仍有很高的测距和测速精度,能满足实际应用要求。
3)同速不同距的多目标仿真分析。选取两个目标,速度为70 m/s,距离分别是10 km和15 km,利用步进频-键控波形处理方法进行仿真,仿真信噪比为5 dB,从仿真结果可以看出,步进频移键控波形处理方法能够较好地分辨同速不同距的多目标。
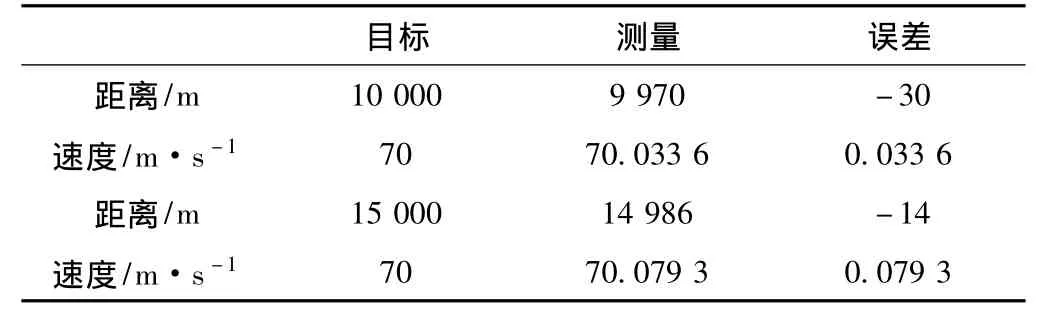
表3 同速度不同距离的多目标仿真
6 结束语
二次相差多频连续波雷达算法结构简单,但不能解决同速度不同距离的多目标分辨问题;步进频率连续波雷达能够解决同速度不同距离的多目标分辨问题,但需要对目标的多普勒效应进行补偿;步进频移键控波形在满足速度和距离探测精度的要求上,解决了同速不同距的多目标分辨问题。
对于速度变换目标的仿真可参照步进频移键控连续波处的讨论,由于信号的发射时间较短,速度变换带来的影响可忽略,仿真采用的匀速运动目标产生的结果符合实际应用。

表4 算法比较
[1]曹延伟.多频连续波雷达跟踪控制器设计及相关理论和算法研究[D].长沙:国防科技大学,2005.
[2]曹延伟,程翥,皇甫堪.多频连续波雷达两种测距算法研究[J].电子与信息学报,2005,27(5):789 -792.
[3]袁俊泉,龚享铱,皇甫堪.基于二次差频的多频连续波测距方法研究[J].电子学报,2004,32(12):2056 -2058.
[4]毛二可,龙腾,韩月秋.频率步进雷达数字信号处理[J].航空学报,2001,22(增刊):16 -25.
[5]Rohling,Herman,Christof Moller.Radar waveform for automotive radar systems and applications[C].Radar Conference,RADAR'08 IEEE,2008.
[6]柏业鑫.多频连续波雷达信号处理算法研究[D].西安:西安电子科技大学,2012.
[7]龙腾.频率步进雷达信号的多普勒性能分析[J].现代雷达,1996,18(2):31-37.

