Multivariable Wavelet Finite Element for Plane Truss Analysis

Xingwu Zhang,Jixuan Liu,Xuefeng Chen,3and Zhibo Yang

Multivariable Wavelet Finite Element for Plane Truss Analysis

Xingwu Zhang1,Jixuan Liu2,Xuefeng Chen1,3and Zhibo Yang1

Plane truss is widely used in mechanical engineering,building engineering and the aerospace engineering et al..The precisely analysis of plane truss is very important for structural design and damage detection.Based on the generalized variational principle and B spline wavelet on the interval(BSWI),the multivariable wavelet finite element for plane truss is constructed.First,the wavelet axial rod element and the multivariable wavelet Euler beam element are constructed.Then the multivariable plane truss element can be obtained by combining these two elements together.Comparing with the traditional method,the generalized displacement and stress are treated as independent variables in multivariable method,so differentiation and integration are avoided in calculation,the efficiency and precision can be improved.Furthermore,compared with commonly used Daubechies wavelet,BSWI has explicit expression and excellent approximation property,which further guarantees satisfactory results.The efficiency of the constructed multivariable wavelet elements is validated through several numerical examples in the end.

Multivariable, B-spline wavelet on the interval, Axial rod, Euler beam,Plane truss.

1 Introduction

In mechanical engineering,building engineering and aerospace engineering,the truss structures are widely used.As the key support component,precise numerical analysis is very important for structural design and damage identification.Based on linear finite element method,Sedaghati developed a structural analysis and optimization method to find the optimal topology of adaptive determinate truss structures[Sedaghati,Suleman,Dost and Tabarrok(2001)].Han analyzed prestressed composite space truss and verified on a physical model test[Han,Yuan,Ying and Liu(2005)].Huang analyzed truss structures with random parameters utilizing recursive stochastic finite element method[Huang,Suo and Mao(2007)].Jiang constructed rectangular truss element based on generalized finite element method[Jiang,Huang and Cao(2007)].Based on finite element model and the vibration data,Huang proposed a damage detection method for plane steel truss[Huang and yang(2010)].Panda applied the meta-models in finite element based reliability analysis for truss structure predication[Panda and Manohar(2008)].Luo developed a finite element method based on the self-defined truss element and analyzed the dynamic characteristic of the corresponding model[Luo,Xu and Zhang(2010)].Torkamani presented a methodology for the elastic large displacement analysis of plane trusses[Torkamani and Shieh(2011)].Song developed a three-dimensional finite element method and studied the critical buckling load and lateral force of metal-plate-connected wood truss assemblies[Song and Lam(2012)].Noilublao proposed a novel integrated design strategy to accomplish simultaneous topology shape and sizing optimization of plane truss structures[Noilublao and Bureerat(2013)].

In the above elements for truss structural analysis,traditional interpolating functions are mainly used to discrete the solving field.Wavelet finite element method is a new numerical method,which takes wavelet and scaling functions as interpolating function.Compared with traditional interpolating functions,wavelet has many good properties,such as multiresolution,orthogonality,compact-supported and so on,so wavelet finite element can do structural analysis with high efficiency and good accuracy and is suitable for singularity problems.Therefore,wavelet finite element method attracted many scholars in the area of numerical analysis,structural analysis and fault diagnosis[Li and Chen(2014)].

In the area of numerical analysis,Gaur developed the wavelet based adaptive solver for two dimensional advection dominating solution problem[Gaur and Singh(20 13)].Wang proposed a new second-generation wavelet-based finite element method for solving partial differential equations[Wang,Chen and He(2012)].Jiwari constructed an efficient numerical scheme based on uniform Haar wavelets and the quasilinearization process for time dependent nonlinear Burgers’equation[Jiwari(2012)].Proppe studied the multiresolution analysis for stochastic finite element problems with wavelet-based Karhunen-Loeve expansion[Proppe(2012)].Based on the modified Hellinger-Reissner variational principle and B-spline wavelet on the interval,Liu derived the Hamilton canonical equation[Liu,Shi,Li and Qing(2011)].Liu proposed a wavelet based method for solving a class of nonlinear time dependent partial differential equations[Liu,Wang and Zhou(2013)].Libre studied the wavelet based adaptive method for solving nearly singular potential PDEs[Libre,Emdadi,Kansa,Shekarchi and Rahimian(2008)].

In the area of structural analysis,Ren constructed wavelet-based stochastic finite element method for thin plate bending analysis based on spline wavelet[Ren,Han and Huang(2007)].Diaz constructed Daubechies wavelet finite element method for beam and plate analysis[Diaz,Martin and Vampa(2009)].Zupan constructed triangular Hermite wavelet finite element for 3D beam analysis[Zupan and Saje(2009)].Liu solved the 2D elastic problems based on quadratic B-spline wavelet finite element method[Liu,Sun and Cen(2011)].Yang analyzed the free vibration of curved shell using B-spline wavelet on the interval and general shell theory[Yang,Chen,Li,He and Miao(2012)].Pahlavan proposed a novel and generic formulation of spectral finite element approach based on Daubechies compactly-supported wavelets for elastic wave propagation simulation[Pahlavan,Kassapoglou and Gurdal(2013)].Tanaka constructed a wavelet Galerkin method based on B-spline wavelet bases for application to solid mechanics problems[Tanaka,Okada and Okazawa(2012)].Chen applied Daubechies wavelet theory to analyze beam of high stress gradient[Chen,Zhang and Dang(2012)].Li adopted adaptive element-free Galerkin method based on B-spline wavelet for rigid plastic simulation[Li and Wang(2012)].Tabrez studied wave propagation in degraded composite beam using wavelet based spectral finite element method[Tabrez,Mitra and Gopalakrishnan(2007)],and developed a 2D wavelet based spectral finite element method in wave propagation analysis of an isotropic plate[Mitra and Gopalakrishnan(2006)].Zhao constructed the Daubechies wavelet finite element for thermal stress distribution analysis of ceramic-coated pistons[Zhao(2012)].Gopikrishna presented a new hierarchical finite element formulation for structural dynamics problems[Gopikrishna and Shrikhande(2011)].Based on the second generation wavelets, He proposed a new beam element multiresolution method[He,Chen and Zhang(2011)].Zuo analyzed the free vibration and buckling problems for functionally graded beam[Zuo,Yang,Chen and Xie(2014a)]and plate[Zuo,Yang,Chen,Xie and Zhang(2014b)]by using B-spline wavelet on the interval finite element method.

In the area of damage detection,Xiang did much work on it.Based on B-spline wavelet on the interval,He constructed the multiple damage detection method for beams based on multi-scale element[Xiang and Liang(2011)],achieved structural damage detection by hybrid of interval wavelet and wavelet finite element model[Xiang,Matsumoto,Wang and Jiang(2011)]and detected crack in plane structures[Xiang,Wang,Jiang,Long and Ma(2012)]and conical shells[Xiang,Matsumoto,Wang and Jiang(2013)].Li developed quantitative identification of multiple cracks in a rotor utilizing wavelet finite element method[Li and Dong(2012)].Wang studied the pipe model for crack detection based on Daubechies wavelet finite element merhod and generic algorithm[Wang,Chen and He(2011)].

Wavelet finite element method attracted many scholars to do research both in numerical calculation,structural analysis and fault diagnosis.However,the above constructed wavelet elements are mainly single variable element,that is,only generalized displacement can be solved directly while generalized stress and strain should be calculated secondary by displacement.So the calculation precision and efficiency will be affected.Atluri et al.,solved this problem by mixed finite element method in which the displacement and strain vectors are all treated and interpolated as independent variables.Several mixed finite elements had been constructed,especially Meshless Local Petrov Galerkin(MLPG)mixed method,including 4-node mixed collocation element[Dong,EI-Gizawy,Juhany and Atluri(2014a)],8-node mixed collocation element[Dong,EI-Gizawy,Juhany and Atluri(2014b)]etc.,which were applied in solving several practical problems,such as macro-µmechanics[Dong and Atluri(2011)],vortex mixing flow[Ruben,Han and Atluri(2011)],heat transfer[Zhang,He,Dong,Li,Alotaibi and Atluri(2014)]and laminated structures[Dong,EI-Gizawy,Juhany and Atluri(2014a)]et al..Several numerical and experimental results proved the efficiency and accuracy of the constructed mixed method.Multivariable wavelet finite element method takes full advantages of mixed finite element method and wavelet interpolation functions,in which the generalized displacement,stress and strain will be interpolated independently by wavelet functions,so the precision and efficiency can be further enhanced and improved.Han proposed multivariable wavelet finite element for Reissner-Mindlin plate static analysis[Han,Ren and Huang(2005)].However,the interpolating wavelet function was taken as interpolating function in his study,which did not have explicit expression,so took many troubles to the differentiation and integration calculation.B-spline wavelet on the interval has explicit expressions and very good approximation properties,Zhang constructed multivariable wavelet finite element method and applied in 1D beam structural analysi[Zhang,Chen,He and Cao(2012)],Reissner-Mindlin plate analysis[Zhang,Chen and He(2011)]and shallow shell analysis[Zhang,Chen,He and Yang(2012)],though numerical examples,the efficiency and precision were verified.

In this study,based on generalized variational principle and B-spline wavelet on the interval,the multivariable wavelet finite element for plane truss is constructed.First,based generalized energy functions,the BSWI axial rod multivariable BSWI Euler beam elements are proposed.Then combining these two elements together,the multivariable BSWI plane truss element is developed.In order to verify the efficiency and advantages of the constructed elements,many numerical examples are proposed in the end.

In section 2,the BSWI scaling functions which are the interpolating functions are presented.According to generalized principle,the multivariable FEM formulations of plane truss are derived in Section 3.Section 4 gives some numerical examples to verify the method proposed in this paper.

2 B-spline wavelet on the interval[0,1]

Chui and Quak constructed B-spline wavelet on the interval [Chui and Quak (1992)],and gave its decomposition and reconstruction algorithm in 1994[Quak and Norman(1994)].In order to have at least one inner wavelet,the following condition must be satisfied.

Where m and j are the order and scale of BSWI respectively.While 0 scale mth order B-spline scaling functions and the corresponding wavelets are given by Goswami J.C.in Ref.[Goswami,Chan and Chui(1995)],j scale mth order BSWI(simply denoted as BSWImj)scaling functionsand the corresponding waveletscan be evaluated by the following formulas.

For the need of the following element construction, the scaling functions and wavelets of BSWI43are given in Fig.1.

The vector form of scaling functions in the lower resolution approximation space Vjare given by

Figure 1:BSWI43on the interval[0,1].

Semi-orthonormal wavelets in detail spaceWjare

3 The construction of multivariable wavelet finite element for plane truss

The multivariable wavelet plane truss element can be constructed by combining BSWI axial rod element and multivariable Euler beam element together.The solving domain and nodes displacement of plane truss are shown in Fig.2.Where(X,Y)is local coordinate andis global coordinate.From Fig.2,it can be seen that there are three degrees of freedom(DOF)at every node,and the total DOFs are 3×(2j+3),where j is the scaling of BSWI scale functions.

Figure 2:The solving domain and nodes displacement of plane truss.

The physical DOFs of multivariable plane truss element in local coordinate are:

while the corresponding DOFs in global coordinate are:

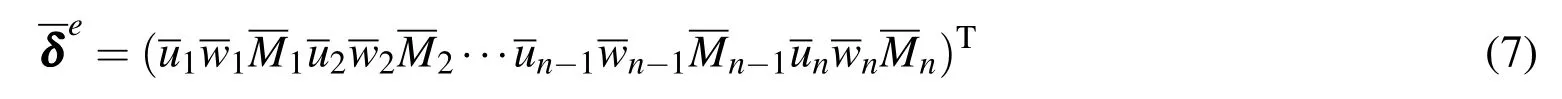
The relationship between global and local coordinates in Fig.2 is shown in the following equation.

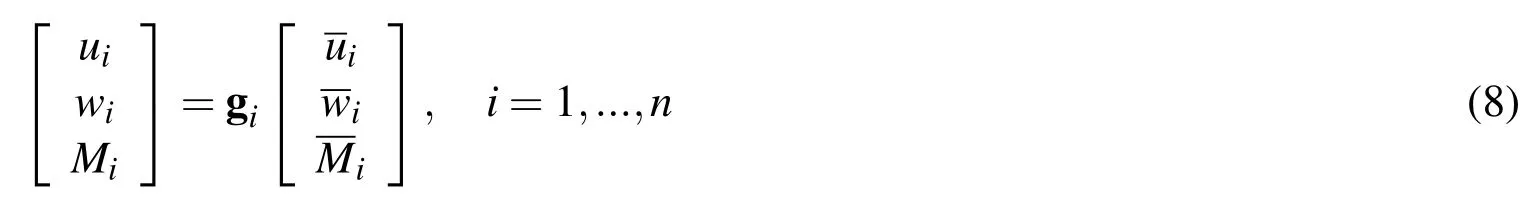
where,

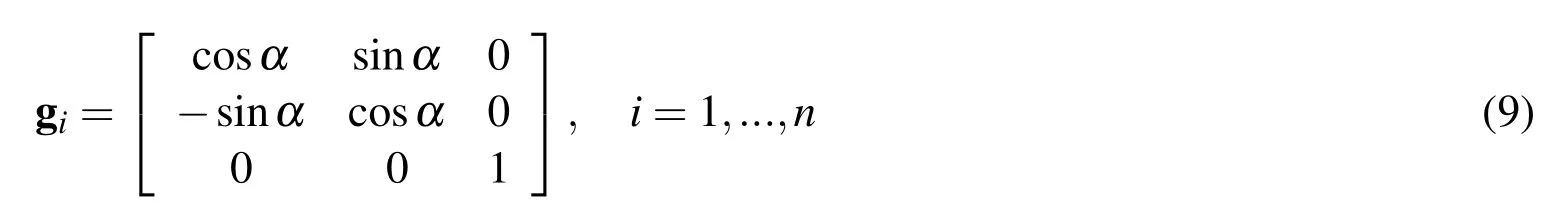
Therefore,the transformation matrix Gebetween local coordinate and global coordinate can be obtained.

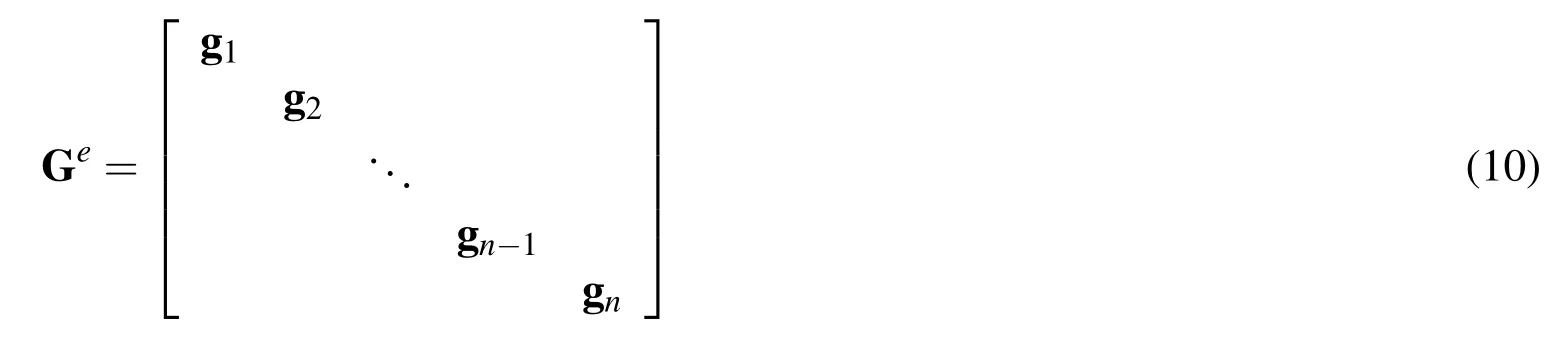
Then,

The corresponding transformation equation of element load is:

Therefore,the finite element function of plane truss in local coordinate is:

Taking equation(7)into(13),and considering transformation matrix,the finite element formula in global coordinate can be obtained.

Where,

The generalized finite element function of plane truss has been obtained,while how to constructed the multivariable wavelet plane truss element,BSWI axial rod element and multivariable BSWI Euler beam element are needed.Therefore,these two elements will be constructed in the following.

3.1 BSWI axial rod element

The nodes displacement of standard axial rod element is shown in Fig.3.

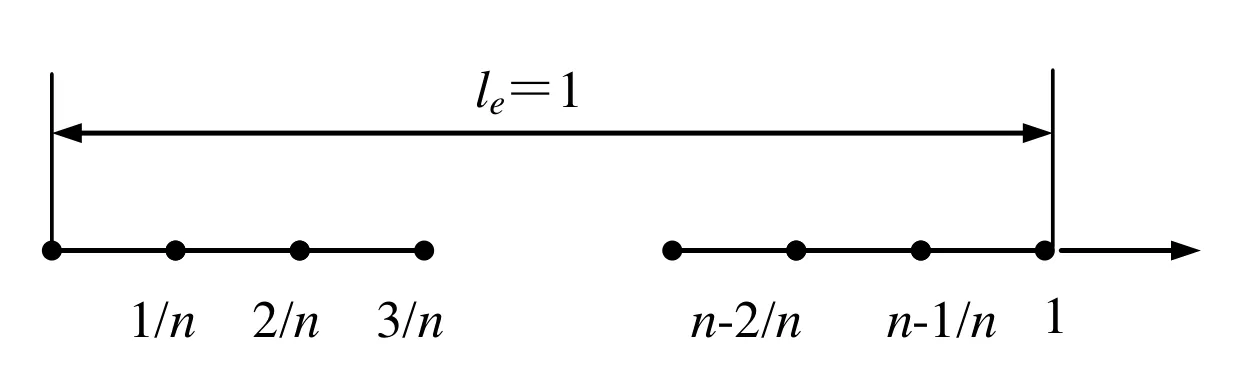
Figure 3:Nodes displacement of axial rod.

The governing equation of axial rod is:

where,E is elastic modulus,A is section area,u is axial displacement and f is the external axial force.

Introducing bilinear functional

and linear functional,

the weak form solution can be obtained by Galerkin or Ritz variational principle.

Where,Vhis the finite dimensional subspace.

By using scaling functions in equation(4)to discrete the field functions,the displacement field function can be obtained as following.

Taking equations(20)-(21)into equation(19),

and taking equations(14)-(15)into equation(22),the solving function for BSWI axial rod finite element can be achieved.

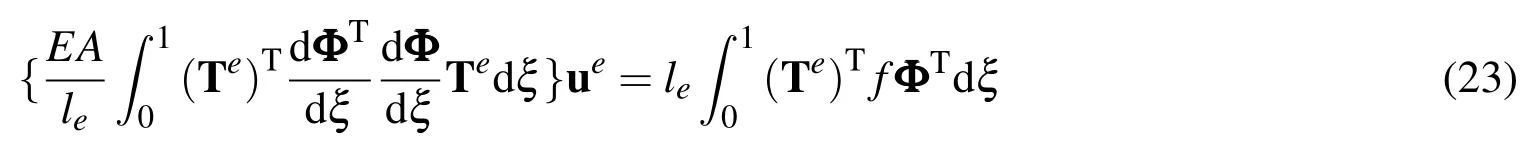
Where,the elemental stiffness matrix is:

and the elemental load vector for distributed load is:

and the elemental load vector for concentrated load can also be acquired.

3.2 Multivariable BSWI Euler beam element

The DOFs displacement of multivariable Euler beam element is shown in Fig.4.There are two DOFs at every node:displacement and moment.

The multivariable generalized potential energy functional is[Shen(1997)]:

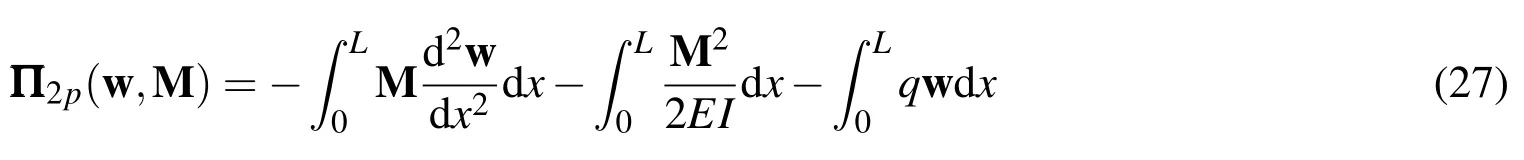
where,EI is flexural rigidity,w is the displacement field function,M is the moment field function and q is the load vector.

Figure 4:The DOFs displacement of multivariable Euler beam element.

BSWI scaling functions in equation(4)is used to discrete the displacement and moment field functions.

According to the multivariable generalized variational principle,andthe multivariable finite element formulation for Euler beam can be achieved as follows.

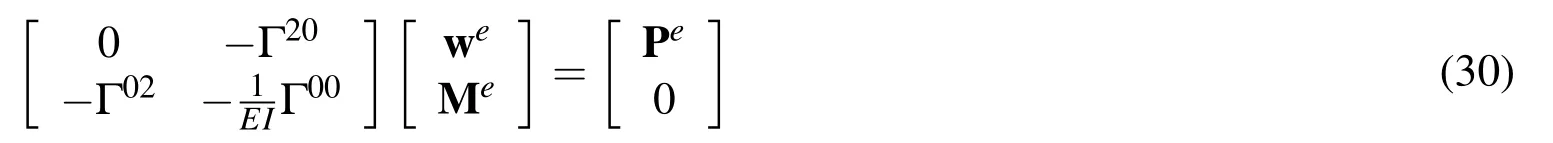
Where,to distributed load,the load vector isto concentrated load.

The integral terms in equation(30)are shown as following.

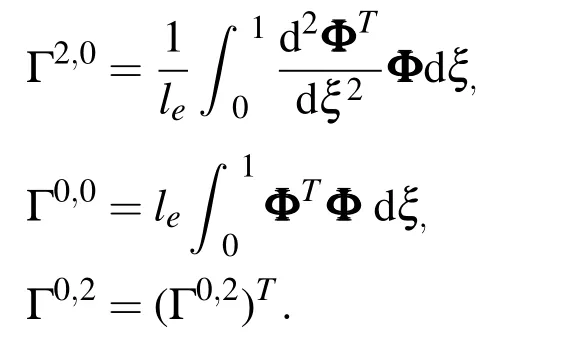
4 Numerical examples

BSWI axial rod element and multivariable BSWI element are constructed first,then combining them together,the multivariable BSWI plane truss element is achieved in section 3.In order to illustrate and prove the efficiency and accuracy of the constructed elements,some numerical examples are given blow in this section,while the constructed multivariable BSWI Euler beam element and plane truss element will also be included.

4.1 Euler beam

As shown in Fig.5,cantilever Euler beam with variable cross section under concentrated load on the free end,the corresponding parameters are:elastic modulus E=1.2×106N/m2,beam width B=0.1m,beam height h(x),beam length L=1m,concentrated load P=1N/m,respectively.

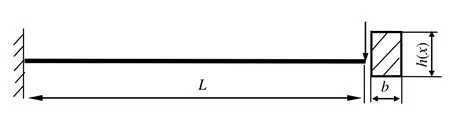
Figure 5:Cantilever Euler beam with variable cross section.

The solving results to cantilever Euler beam with variable beam height changing in first law function h(x)=(1−0.9(x/L))/10 is shown in Fig.6.The results of multivariable wavelet finite element based on B-spline wavelet on the interval(MBSWI)are compared with theoretical solution.It can be seen that the MBSWI results are in consistent with theoretical solution.Table 1 shows the solving results of cantilever beam with variable beam height changing in secondary law h(x)=(1+0.9(x/L)−1.8(x/L)2)/10.The solving results of MBSWI to displacement,slope and moment are compared with BSWI element and theoretical solution.To displacement solution,MBSWI and BSWI all has good solution precision.However,to slope and moment,MBSWI is better than BSWI element,and MBSWI element results are more close to the theoretical solution.Therefore,the calculation advantages of the constructed MBSWI Euler element are proved.

4.2 plane truss

Example 1:as shown in Fig.7,the plane truss is simply supported with horizontal distributed load.The corresponding parameters are:EA=10kN,EI=10/12kN/m2,and L=1m respectively.and q=1kN.

First,the plane truss with regular distributed horizontal load(q=1kN)is investigated.The solving results of plane truss deformation and slope along OAB are shown in Fig.8.MBSWI solution is compare with ANSYS BEAM3 element.In this example,the plane truss is discretized with 1 MBSWI element and 32 ANSYS BEAM3 elements,and the analysis results are highly in consistent with each other.However,MBSWI has 63 DOFs and ANSYS BEAM3 has 99 DOFs in solving this problem.

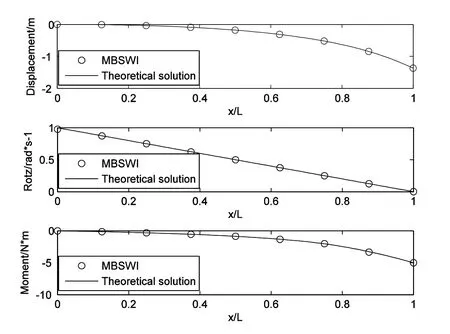
Figure 6:Solving results of cantilever Euler beam with variable cross section(Beam height h(x)=(1−0.9(x/L))/10).

Figure 7:Plane truss under horizontal distributed load.

?

Figure 8:Analysis results of plane truss with horizontal distributed load(q=1kN).

Then,the horizontal distributed load is increased to be 10kN(q=10kN),and the analyzed results of this large deformation case is shown in Fig.9.Similar to the case with regular load,the results are compared between MBSWI and ANSYS element.It can be seen clearly from Fig.9 that MBSWI element can achieve similar accuracy with ANSYS,while only one element is used by MBSWI and 32 elements are used by ANSYS.Therefore,the constructed MBSWI element is suitable for both regular deformation and large deformation analysis with good solving efficiency and accuracy.

Example 2:as shown in Fig.10,the plane truss is simply supported with vertical distributed load.The corresponding parameters are:EA=10kN,EI=10/12kN/m2,L=1m,respectively.

Similar as example 1,the plane truss with regular load(q=1kN)is investigated first.Fig.11 shows the solving results of plane truss with vertical distributed load.The analysis solution of MBSWI element are also compared with ANSYS BEAM3 element.It can be seen that the results of MBSWI element(63DOFs)coincides with ANSYS BEAM3 element(99DOFs),while solving efficiency of MBSWI is better.

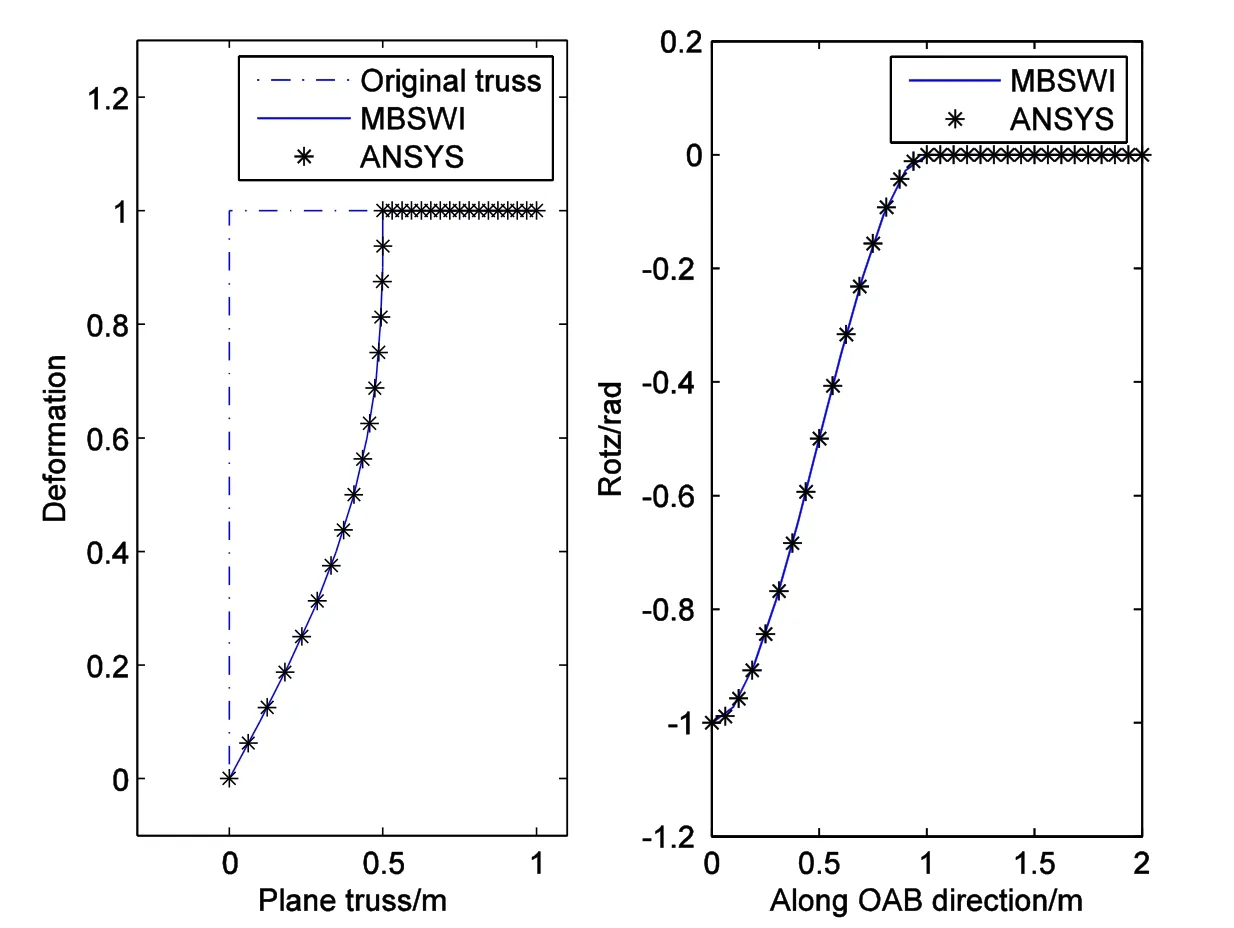
Figure 9:Analysis results of plane truss with horizontal distributed load(q=10kN).

Figure 10:Plane truss under vertical distributed load.

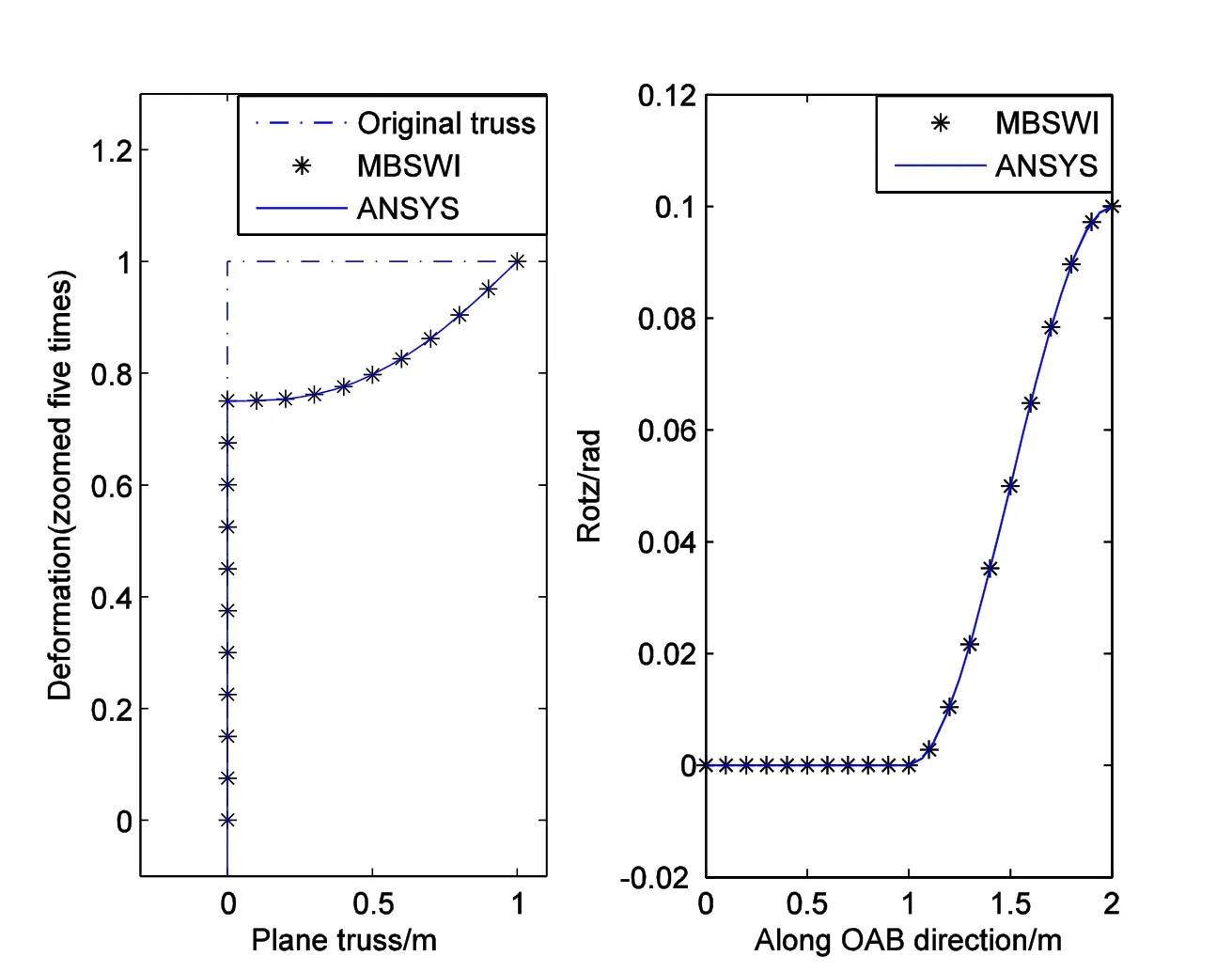
Figure 11:Analysis results of plane truss with vertical distributed load(q=1kN).

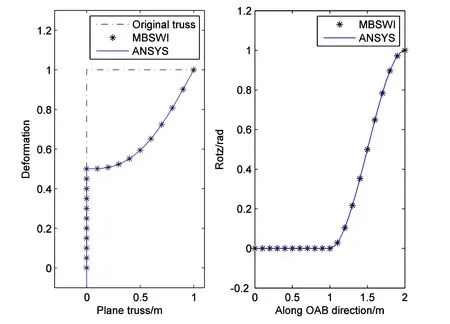
Figure 12:Analysis results of plane truss with vertical distributed load(q=10kN).

Then,the plane truss with increased load(q=10kN)is investigated to simulate the large deformation case.It can be seen from the results in Fig.12 that MBSWI can still achieve accurate analysis results with only 2/3 computational amount compared with ANSYS.Therefore,the advantages of multivariable wavelet plane truss element is proved by these two examples under two different load conditions.

5 Conclusion

Based on B spline wavelet on the interval and the generalized variational principle,the multivariable wavelet plane truss element is constructed in this paper.First,the wavelet axial rod element and the wavelet Euler beam element based on B-spline wavelet on the interval are constructed.Then combining these two constructed elements,the multivariable wavelet plane truss element is obtained.In the construction process,the generalized displacement and the generalized stress are interpolated by BSWI scaling functions,so the secondary calculation is avoid and the calculation precision is improved.Through several numerical examples,it proved that the constructed multivariable BSWI Euler beam element and the multivariable BSWI plane truss element has very good calculation efficiency and precision,and is suitable for mechanical structural analysis.

Acknowledgement:This work was supported by the National Natural Science Foundation of China(Nos.51405370&51225501),the project supported by Natural Science Basic Research Plan in Shaanxi Province of China(No.2015JQ5184),the Fundamental Research Funds for the Central Universities(No.xjj2014014),the project funded by China Postdoctoral Science Foundation(No.2014M552432).

Chen,Y.Q.;Zhang,H.G.;Dang,F.N.(2012):Applying Daubechies wavelet theory to compute beam of high stress gradient.Engineering Journal of Wuhan University,vol.45,pp.65-69.

Chui,C.K.;Quak,E.(1992):Wavelets on a bounded interval.Numerical Methods of Approximation Theory,vol.1,pp.53-57.

Diaz,L.A.;Martin,M.T.;Vampa,V.(2009):Daubechies wavelet beam and plate finite element.Finite Elements in Analysis and Design,vol.45,pp.200-209.

Dong,L.T.;Atluri,S.N.(2011):A simple procedure to develop efficient&stable hybrid/mixed elements,and voronoi cell finite elements for macro-µmechanics.CMC-Computers Materials&Continua,vol.24,pp.61

Dong,L.T.;EI-Gizawy,A.S.;Juhany,K.A.;Atluri,S.N.(2014a):A simple locking-alleviated 4-node mixed-collocation finite element with over-integration,for homogeneous or functionally-graded or thick-section laminated composite beam-s.CMC-Computers,Materials&Continua,vol.40,pp.49-77.

Dong,L.T.;EI-Gizawy,A.S.;Juhany,K.A.;Atluri,S.N.(2014b):A simple locking-alleviated8-node mixed-collocation C0 finite element with over-integration,for functionally-graded or laminated thick-section plates and shells,with&withour Z-Pins.CMC-Computers,Materials&Continua, vol.41,pp.163-192.

Gaur,S.;Singh,L.P.;Singh,V.;Singh,P.K.(2013):Wavelet based multiscale scheme for two-dimensional advection-dispersion equation.Applied Mathematical Modelling,vol.37,pp.4023-4034.

Gopikrishna,K.;Shrikhande,M.(2011):Wavelet basis finite element solution of structural dynamics problems.Engineering Computations,vol.28,pp.275-286.

Goswami,J.C.;Chan,A.K.;Chui,C.K.(1995):On solving first-kind integral equations using wavelets on a bounded interval.IEEE Transactions on Antennas and Propagation,vol.43,pp.614-622.

Han,J.G.;Ren,W.X.;Huang,Y.(2005):A multivariable wavelet-based finite element method and its application to thick plates.Finite Elements in Analysis and Design,vol.41,pp.821-833.

Han,Q.H.;Yuan,Z.H.;Ying,M.;Liu,X.L.(2005):Numerical analysis and experimental study of prestressed diagonal-on-square composite space truss.Advances in Structural Engineering,vol.8,pp.397-410.

He,Y.M.;Chen,X.;Zhang,X.L.(2011):Construction of the beam element based second generation wavelet.Applied Mechanics and Materials,vol.80-81,pp.532-535.

Huang,B.;Suo,J.C.;Mao,W.J.(2007):Geometrical nonlinear analysis of truss structures with random parameters utilizing recursive stochastic finite element method.Acta Mechanica Sinica,vol.39,pp.835-842.

Huang,H.W.;Yang,J.N.(2010):Damage identification of a plane steel truss with incomplete measurements.Conference on Sensors and Smart Structures Technologies for Civil,Mechanical,and Aerospace Systems,San Diego,CA,March 08-11.

Jiang,F.;Huang,L.;Cao X.(2007):Object-oriented programming of rectangular truss element.The 4th International Conference on Structural Engineering and Construction,Melbourne,Australia,September,26-18.

Jiwari,R.(2012):A Haar wavelet quasilinearization approach for numerical simulation of Burgers’equation.Computer Physics Communications,vol.183,pp.2413-2423.

Libre,N.A.;Emdadi,A.;Kansa,E.J.;Shekarchi,M.;Rahimian,M.(2008):A fast adaptive wavelet scheme in RBF collocation for nearly singular potential PDEs.CMES-Computer Modeling in Engineering&Sciences,vol.38,pp.263-284.

Li,B.;Chen,X.F.(2014):Wavelet-based numerical analysis:a review and classification.Finite Elements in Analysis&Design,vol.81,pp.14-31.

Li,B.;Dong,H.B.(2012):Quantitative identification of multiple cracks in a rotor utilizing wavelet finite element method. CMES-Computer Modeling in Engineering&Sciences,vol.84,pp.205-228.

Li,D.;Wang,C.P.(2012):Adaptive element-free Galerkin method based on B-spline wavelet for rigid plastic simulation.Journal of Mechanical Strength,vol.34,pp.551-556.

Liu,Y.H.;Shi,Y.S.;Li,D.H.;Qing,G.H.(2011):B-spline wavelet on the interval element for the solution of Hamilton canonical equation.Mechanics of Advanced Materials and Structures,vol.18,pp.446-453.

Liu,Y.N.;Sun,L.;Liu,Y.H.;Cen,Z.Z.(2011):Multi-scale B-spline method for 2-D elastic problems.Applied Mathematical Medelling,vol.35,pp.3685-3697.

Liu,X.J.;Wang,J.Z.;Zhou,Y.H.(2013):A wavelet method for solving nonlinear time-dependent partial differential equations.CMES-Computer Modeling in Engineering&Sciences,vol 94,pp.225-238.

Luo,Y.J.;Xu,M.L.;Zhang,X.N.(2010):Nonlinear self-defined truss element based on the plane truss structure with flexible connector.Communications in Nonlinear Science and Numerical Simulation,vol.15,pp.3156-3169.

Mitra,M.;Gopalakrishnan,S.(2006):Wavelet based 2-D spectral finite element formulation for wave propagation analysis in isotropic plates.CMES:Computer Modeling in Engineering&Sciences,vol.15,pp.49-67.

Noilublao,N.;Bureerat,S.(2013):Simultaneous topology,shape,and sizing optimization of plane trusses with adaptive ground finite element using MOEAs.Mathematical Problems in Engineeing,838102.

Pahlavan,L.;Kassapoglou,C.;Gurdal,Z.(2013):Spectral formulation of finite element methods using Daubechies compactly-supported wavelets for elastic wave propagation simulation.Wave Motion,vol.50,pp.558-578.

Panda,S.S.;Manohar,C.S.(2008):Application of meta-models in finite element based reliability analysis of engineering structures.CMES:Computer Modeling in Engineering&Sciences,vol.28,pp.161-184.

Proppe,C.(2012):Multiresolution analysis for stochastic finite element problems with wavelet-based Karhunen-Loeve expansion.Mathematical Problems in Engineering,215109.

Quak,E.;Norman,W.(1994):Decomposition and reconstruction algorithms for spline wavelets on a bounded interval.Applied and Computational Harmonic Analysis,vol.1,pp.217-231.

Ren,W.X.;Han,J.G.;Huang,Y.(2007):A wavelet-based stochastic finite element method of thin plate bending.Applied Mathematical Modelling,vol.31,pp.181-193.

Ruben,A.;Han,Z.D.;Atluri,S.N.(2011):A novel MLPG-finite-volume mixed method for analyzing Stokesian flows&study of a new vortex mixing flow.CMES Computer Modeling in Engineering&Sciences,vol.71,pp.363-396.

Sedaghati,R.;Suleman,A.;Dost,S.;Tabarrok,B.(2001):Optimum design of adaptive truss structures using the integrated force method.CMES:Computer Modeling in Engineering&Sciences,vol.2,pp.259-271.

Shen,P.C.(1997):Multivariable spline finite element method,Science press,Beijing.

Tabrez,S.;Mitra,M.;Gopalakrishnan,S.(2007):Modeling of degraded composite beam due to moisture absorption for wave based detection.CMES:Computer Modeling in Engineering&Sciences,vol.22,pp.77-89.

Tanaka,S.;Okada,H.;Okazawa,S.(2012):A wavelet Galerkin method employing B-spline bases for solid mechanics problems without the use of a fictitious domain.Computational Mechanics,vol.50,pp.35-48.

Torkamani,M.A.M.;Shieh,J.H.(2011):Higher-order stiffness matrices in nonlinear finite element analysis of plane truss structures.Engineering Structures,vol.33,pp.3516-3526.

Wang,Y.M.;Chen,X.F.;He,Z.J.(2012):A second-generation wavelet-based finite element method for the solution of partial differential equations.Applied Mathematical Letters,vol.25,pp.1608-1613.

Wang,Y.M.;Chen,X.F.;He,Z.J.(2011):Daubechies wavelet finite element method and genetic algorithm for detection of pipe crack.Nondestructive Testing and Evaluation,vol.26,pp.87-99.

Xiang,J.W.;Liang,M.(2011):Multiple damage detection method for beams based on multi-scale elements using hermite cubic spline wavelet.CMES:Computer Modeling in Engineering&Sciences,vol.73,pp.267-298.

Xiang,J.W.;Matsumoto,T.;Wang,Y.X.;Jiang,Z.S.(2011):A hybrid of interval wavelets and wavelet finite element model for damage detection in structures.CMES:Computer Modeling in Engineering&Sciences,vol.81,pp.269-294.

Xiang,J.W.;Matsumoto,T.;Wang,Y.X.;Jiang,Z.S.(2013):Detect damages in conical using curvature mode shape and wavelet finite element method.Interna-tional Journal of Mechanical Sciences,vol.66,pp.83-93.

Xiang,J.W.;Wang,Y.X.;Jiang,Z.S.;Long,J.Q.;Ma,G.(2012):Numerical simulation of plane crack using Hermite cubic spline wavelet.CMES:Computer Modeling in Engineering&Sciences,vol.88,pp.1-15.

Yang,Z.B.,Chen,X.F.;Li,B.;He,Z.J.;Miao,H.H.(2012):Vibration analysis of curved shell using B-spline wavelet on the interval(BSWI)finite elements method and general shell theory.CMES:Computer Modeling in Engineering&Sciences,vol.185,pp.129-155.

ZhangT.,HeY.,DongL.T.,LiS.,AlotaibiA.,AtluriS.N.(2014):Meshlesslocal petrov-galerkin mixed collocation method for solving Cauchy inverse problems of steady-state heat transfer.CMES-Computer Modeling in Engineering&Sciences,vol.97,pp.509-553.

Zhang,X.W.;Chen,X.F.;He,Z.J.(2011):The construction of multivariable Reissner-Mindlin plate elements based on B-spline wavelet on the interval.Structural Engineering and Mechanics,vol.38,pp.733-751.

Zhang,X.W.;Chen,X.F.;He,Z.J.;Cao,H.R.(2012):The multivariable finite elements based on B-spline wavelet on the interval for 1D structural mechanics.Journal of Vibroengineering,vol.14,pp.363-380.

Zhang,X.W.;Chen,X.F.;He,Z.J.;Yang,Z.B.(2012):The analysis of shallow shell based on multivariable wavelet finite element method.Acta Mechanica Solida Sinica,vol.24,pp.450-460.

Zhao,B.(2012):Thermal stress analysis of ceramic-coated diesel engine pistons based on the wavelet finite element method.Journal of Engineering Mechanics-ASCE,vol.138,pp.143-149.

Zuo,H.;Yang,Z.B.;Chen,X.F.;Xie,Y.(2014a):Static,free vibration and buckling analysis of functionally graded beam via B-spline wavelet on the interval and Timoshenko beam theory.CMES-Computer Modeling in Engineering&Sciences,vol.100,pp.477-506.

Zuo,H.;Yang,Z.B.;Chen,X.F.;Xie,Y.;Zhang,X.W.(2014b):Bending,free vibration and buckling analysis of functionally graded plates via wavelet finite element method.CMC-Computers,Materials&Continua,vol.44,pp.167-204.

Zupan,E.;Zupan,D.;Saje,M.(2009):The wavelet-based theory of spatial naturally curved and twisted linear beams.Computational Mechanics,vol.43,pp.675-686.

1State Key Laboratory for Manufacturing System Engineering,School of Mechanical Engineering,Xi’an Jiaotong University,Xi’an 710049,PR China.

2The National Demonstration Center of Experimental Teaching,School of Mechanical Engineering,Xi’an Jiaotong University,Xi’an 710049,PR China.

3Corresponding author.Tel:+86 29 82667963;Fax:+86 29 82663689;

E-mail:chenxf@mail.xjtu.edu.cn