利用气动力的大气制动过程中近心点高度控制

季英良，朱宏玉，杨博

(北京航空航天大学 宇航学院，北京100191)

利用大气阻力实现制动变轨可以节省燃料.已有多次星际探测任务用到了大气制动技术，如Magellan，Mars Global Surveyor，Mars Odyssey 及Mars Reconnaissance Orbiter［1-3］.从实际探测任务来看，大气制动技术的确可以节省可观的燃料.

随着航天技术的发展，大气制动中的控制问题得到了国内外学者关注［4-9］.文献［4］研究了单次穿越大气的控制问题.文献［5］给出了一种用于大气辅助变轨的显式制导方程.实际大气制动过程中，随着航天器穿越大气的次数增加，轨道的远心点和近心点不断降低［6］.近心点降低会带来负面影响:一是近心点过快降低会导致热流密度增加、动压增大等一系列危及航天器安全的问题;二是增加了退出大气制动时提升近心点所需的燃料消耗.对于这一问题，已有的解决方案大体分为两种:一种是通过提高大气制动开始时的近心点高度来保证制动末期近心点高度满足要求，其代价是延长了大气制动所需的时间;另一种是通过对近心点高度预测，必要时在远心点实施额外的轨道调整动作，其代价是增加了燃料消耗［10-13］.

笔者针对大气制动过程中近心点降低的问题，给出一种无需燃料消耗即可控制轨道近心点高度的方法.该方法通过改变倾侧角调整气动力在高度方向上的分量来实现对近心点高度的控制，并且根据当前近心点高度与预定高度的差值自动调整反馈增益.仿真结果显示，此方法可以在整个制动过程中限制轨道近心点下降，并最终减少降低量，不但解决了近心点下降引起的额外燃料消耗问题，还保证了航天器的飞行安全.

1 航天器质心运动方程

无推力且不考虑大气随中心天体运动的情况下，航天器在大气中的运动方程可解耦为横向运动方程和纵向运动方程［4］.以倾侧角作为控制变量，横向运动和纵向运动可分开控制.由于近心点下降与纵向运动有关，因此只讨论纵向运动方程:

式中，r为航天器轨道矢径;v为航天器飞行速度;γ为轨迹倾角;D为气动阻力;L为气动升力;σ为倾侧角;m为航天器质量;g为重力加速度，满足g=μ/r2，μ为中心天体引力常量.

气动力满足

式中，CD，CL分别为阻力系数和升力系数;S为航天器有效面积;ρ为大气密度.

采用以下变量:

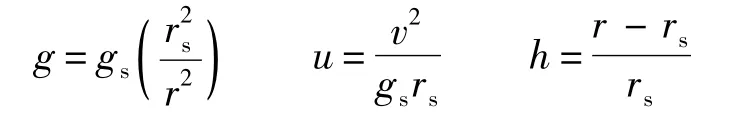
并引入时间量 τ=Vst/rs，对式(1)无量纲化.其中为时间;下标s表示参考轨道的相关参数.

h，u，γ 分别对 τ求导可得

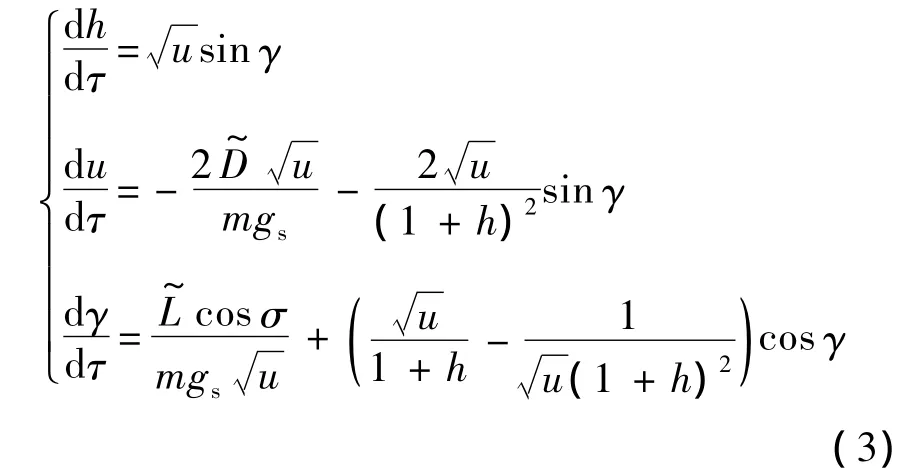
2 大气内飞行控制律

以倾侧角σ作为控制变量.由式(3)可导出h对τ的二阶导数:

考虑常飞行高度变化率d2h/dτ2=0，并将实际飞行高度与参考高度的差、实际飞行高度变化律与参考高度变化律的差作为反馈，可得:

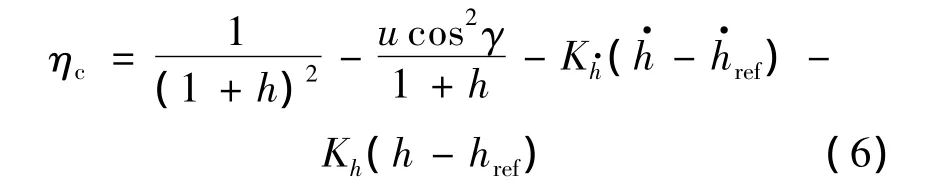
式中，Kh为高度差反馈增益;为高度变化率差反馈增益;href为参考高度为参考高度变化率.

由式(5)可解得

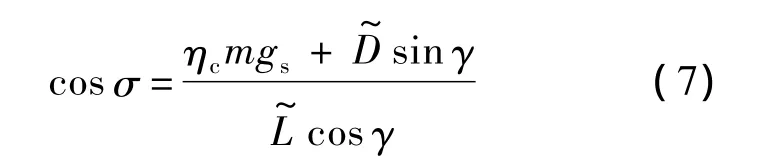
式中gs和m为常量.

仅考虑近心点附近的短时间飞行时，飞行速度v变化小，可视为常量;轨道高度变化小，大气密度ρ可视为常量.假设航天器以平衡攻角飞行，则升力系数CL和有效面积S可视为常量.基于以上假设，根据式(3)，可将式(7)中的视为常量.

再注意到在近心点附近，轨迹倾角γ→0，故 sinγ→0，cosγ→1，式(7)可写成

式中K为常系数.

考虑到cosσ∈［－1，1］，故实际倾侧角为

式中 σ∈［0，π］.

至此，得到了以倾侧角为控制变量的大气内飞行控制律.

3 倾侧角机动与控制律反馈增益

假设已知制动轨道近心点参考高度href，当href未知时需另作讨论.令=0，即大气内参照恒定高度飞行.设大气内飞行时测量ti(i=1，2，…)时刻的参考高度为hi，参考高度变化率为，轨迹倾角为γi，航天器飞行速度为vi，由式(6)和式(9)可得到ti时刻的目标倾侧角σi.

航天器在大气中以零侧滑角飞行时倾侧角与滚转角可视为等同，因此得到σi后可通过控制滚转角实现对倾侧角的机动操作.

随着穿越大气次数增加，航天器的飞行状态会发生很大变化.受飞行状态影响，多次穿越大气后需重新整定控制律反馈增益.这里可依据飞行状态变化量进行整定，也可以依据实际近心点高度的变化来整定.采用何种整定方法需依据实际飞行任务选取.

令 ei=(hp(i－1)－ href)/href(i=2，3，…)，其中，hp(i－1)为第i－1次穿越大气时的实际近心点高度，则

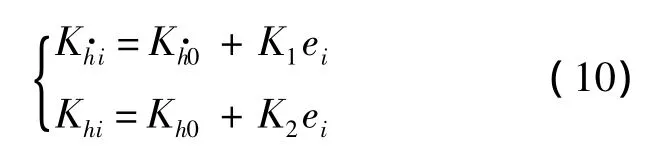
至此给出了一种计算控制律反馈增益的方法.

4 仿真算例

为验证控制律的正确性与可行性，参考文献［13］给出的仿真算例(仿真用到的数据如表1所示)，并以文献［14］介绍的姿态控制律为参考给出对反作用轮性能要求的仿真估计.

表1 仿真中用到的参数Table1 Parameters used in simulation

仿真中选取火星半径圆轨道为参考轨道.火星大气密度满足 ρ=ρ0e(－h/h0)，其中，h为距离火星表面的高度;ρ0为参考密度，取为 1.474×10－2kg/m3;h0为参考高度，取为 8.8057 km［6］.

仿真中动压计算公式为 P=ρv2/2［12］;热流密度经验公式为

首先，对倾侧角分别为固定值(σ=0，π)和受控两种飞行状态进行仿真比较.

图1给出了开普勒轨道近心点高度和实际近心点高度随穿越大气次数的变化曲线.从图中可以看出，σ为固定值时，进入大气的开普勒轨道近心点随穿越大气次数增加而逐渐降低，且下降速率逐渐增大;σ受控时，控制律通过改变倾侧角调整飞行状态，将再次进入大气的开普勒近心点维持在预定值附近.从图中还可以看出，两种飞行状态下实际近心点高度与开普勒近心点高度具有相同的变化趋势，只是变化量有微小的差别.

图1 近心点高度随穿越大气次数的变化Fig.1 Variation of perigee altitude verses the time of atmosphere traversing

图2给出了实际近心点与开普勒近心点高度差随穿越大气次数的变化曲线.从图中可以看出:σ受控时，实际近心点与开普勒近心点高度差较小且保持稳定;σ=π时，随着穿越大气次数增加，实际近心点与开普勒近心点间距逐渐增大;σ=0时，实际近心点较开普勒近心点呈先缓慢升高后降低的变化趋势，高度差相对较小.

图2 近心点高度差随穿越大气次数的变化Fig.2 Variation of perigee-height-difference verses the time of atmosphere traversing

图3给出了穿越大气时最大热流密度、最大动压随穿越大气次数的变化曲线.从图中可以看出，σ固定时，最大热流密度呈先降低后升高的趋势，最大动压持续升高且制动后期上升速率快速增大;σ受控时，最大热流密度一直保持下降趋势，最大动压同样保持缓慢下降趋势.因此，σ受控时，只要初始制动飞行是安全的，那么接下来的制动飞行中可充分保证航天器的安全.

图4给出了远心点随穿越大气次数的变化曲线.从图中可以看出，两种飞行状态以相同初始轨道进行制动飞行时，σ受控时远心点下降速度较缓慢.这与σ受控时近心点下降受到限制有关.因为近心点下降得到了控制，所以在保证制动安全的条件下，可以通过降低σ受控时初始制动轨道的近心点来提高制动效率.

图3 最大热流密度、动压随穿越大气次数的变化Fig.3 Variation of max-heating-rate and max-dynamic-pressure verses the time of atmosphere traversing

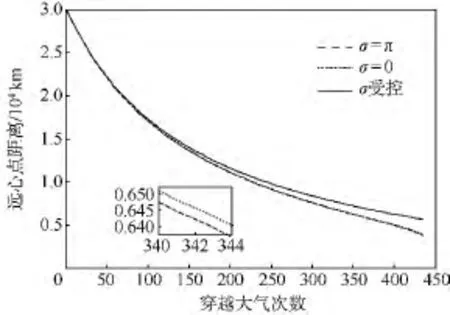
图4 远心点随穿越大气次数的变化Fig.4 Variation of apogee verses the time of atmosphere traversing

表2给出了经过435次穿越大气后的相关轨道参数值.由表中数据可知，σ受控时实际近心点高度几乎未发生变化.从表中还可以看出，相同初始制动轨道条件情况下，经过435次穿越大气后，σ受控时的远心点较σ=0时高出约1800 km，较σ=π时高出约1900 km.

表2 435次穿越大气后轨道参数值Table2 Orbit parameters after 435th atmosphere traversing

周期/h 1.83 1.88 2.60

其次，对σ受控时的制动效率进行仿真验证.延长σ受控时穿越大气的次数，使制动结束时的轨道达到与σ=0时近似的状态，结果如表3所示.

表3 σ受控，完成制动后的轨道参数值Table3 Orbit parameters after finished aerobraking，σ controlled

从表3中可以看出，相同初始制动轨道下，σ受控时达到与σ=0时近似的制动状态需要545次穿越大气，较σ=0时增加了110次.比较表2与表3中的数据可知，制动完成时，σ受控时的实际近心点比σ=0时高出约9.5 km，近心点下降得到有效的限制.

图5给出了延长制动次数后的开普勒近心点和实际近心点的变化曲线.从图中可以看出，前470次穿越大气时轨道近心点维持在href附近，第470次穿越大气后轨道近心点出现下降趋势.导致该现象的原因是制动后期飞行状态变化量较大，仅靠气动力不能有效地限制近心点下降.完成制动时近心点仅降低了约400 m，与近心点高度相比可忽略.

图5 σ受控，近心点高度随穿越大气次数的变化Fig.5 Variation of perigee verses the time of atmosphere traversing，σ controlled

图6给出了第100，200，300和400次穿越大气时的倾侧角变化曲线.从图中可以看出，倾侧角在航天器刚进入大气时为0 rad，经过一段时间的飞行后逐渐变化到π rad，直到逸出大气;随着飞行状态的变化，穿越大气所用的时间逐渐延长.

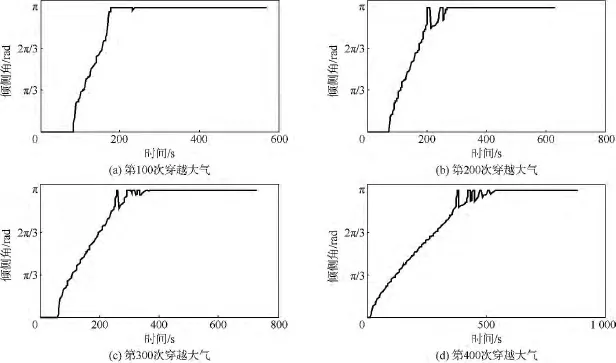
图6 单次大气穿越过程中倾侧角的变化Fig.6 Variation of bank angle during single-pass aerobraking

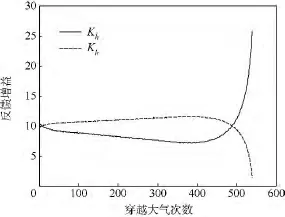
图7 反馈增益随穿越大气次数的变化Fig.7 Variation of feedback gain verses the time of atmosphere traversing

为利用反作用轮实现对倾侧角的机动，最后对反作用轮的性能要求进行仿真估计.参照图6中单次穿越大气时倾侧角的变化曲线，这里直接将倾侧角由0 rad机动到πrad.

假设单次穿越大气需600s，100s前保持倾侧角为0 rad，100 s开始机动到πrad并保持稳定;在整个大气过程中不受外界滚转力矩干扰;航天器转动惯量为 Ix=492，Iy=516，Iz=183 kg·m2;反作用轮转动惯量为0.2 kg·m2.

图8 倾侧角与反作用轮转速变化Fig.8 Variation of bank angle and reaction-wheel speed

控制律中采用指数反馈增益，仿真如图8所示.从图中可以看出，在［0，100)s范围内倾侧角稳定在0 rad，100 s开始机动，经过大约90 s到达πrad.这近似达到了姿态机动对时间的要求.从图中可以看出，满足以上机动要求需要反作用轮的最高转速约为9000 rad/min.

5 结论

针对大气制动过程中存在的近心点降低问题，给出了一种无需燃料消耗即可控制轨道近心点高度的方法.整个大气制动过程中，该方法可以有效地限制近心点降低并最终减少近心点的降低量.这可以节省退出大气制动时提升近心点所用的燃料.因为近心点下降得到了控制，所以在保证安全的条件下，可以通过降低初始制动轨道近心点高度来提高制动效率.该方法的另一个优点是整个制动过程中最大热流密度及最大动压一直呈下降趋势，无需在制动过程中提升轨道近心点，这同样可以节省燃料.

References)

［1］ Spencer D A，Tolson R.Aerobraking cost and risk decisions［J］.Journal of Spacecraft and Rockets，2007，44(6):1285-1293.

［2］ 韩波，张文普.行星探测中的大气制动技术研究进展［J］.力学进展，2010，40(6):642-651.Han B，Zhang W P.Advances of aerobraking technology in the planetary mission［J］.Advance in Mechanics，2010，40(6):642-651(in Chinese).

［3］ 艾远行，乔栋.火星探测气动捕获技术研究进展［C］//中国宇航学会深空探测技术专业委员会第九届学术年会论文集(上册).北京:中国宇航学会深空探测技术专业委员会，2012:58-63.Ai Y X，Qiao D.The research progress of pneumatic capture technology in Mars detection［C］//Proceedings of the 9th Committee of Deep Space Exploration Technology，Chinese Society of Astronautics(Vol.1).Beijing:Committee of Deep Space Exploration Technology，Chinese Society of Astronautics，2012:58-63(in Chinese).

［4］ Miele A，Wang T.Robust predictor-corrector guidance for aeroassisted orbital transfer［J］.Journal of Guidance，Control and Dynamics，1996，19(5):1134-1141.

［5］ Kuo Z S，Liu K C.Explicit guidance of aeroassisted orbital transfer using matched asymptotic expansions［J］.Journal of Guidance，Control and Dynamics，2002，25(1):80-87.

［6］ 陈统，徐世杰.火星轨道大气制动策略研究［C］//全国第14届空间及运动体控制技术学术会议论文集，2010:129-134.Chen T，Xu S J.Research on Mars orbit aerobraking strategy［C］//Proceedings of the 14th National Academic Conference on Space and Moving-body Control Technology，2010:129-134(in Chinese).

［7］ Rozanov M，Guelman M.Aeroassisted orbital maneuvering with variable structure control［J］.Acta Astronautica，2008，62(1):9-17.

［8］ 张海联，吴德隆.热流限制下的最优气动力辅助变轨［J］.上海航天，1999，16(4):6-11.Zhang H L，Wu D L.Aeroassisted optimal orbital transfer problem with heat-flow constraint［J］.Aerospace Shanghai，1999，16(4):6-11(in Chinese).

［9］ 南英，肖业伦，陈士橹.同一平面气动力辅助变轨的近似解及分析［J］.北京航空航天大学学报，1998，24(1):120-123.Nan Y，Xiao Y L，Chen S L.Approximate solutions of the optimal aeroassisted coplanar transfer of space vehicle［J］.Journal of Beijing UniversityofAeronauticsand Astronautics，1998，24(1):120-123(in Chinese).

［10］ Long S M，You T H，Halsell C A，et al.Mars reconnaissance orbiter aerobraking navigation operation［C］//SpaceOps 2008 Conference.Reston，VA:American Institute of Aeronautics and Astronautics Inc，2008:3394.

［11］ Chapel J D，Johnson M A，Sidney W P，et al.Aerodynamic safing approach for the 2001 Mars odyssey spacecraft during aerobraking［J］.Journal of Spacecraft and Rockets，2005，42(3):416-422.

［12］ Lyons D T，Beerer J G，Esposito P，et al.Mars global surveyor:aerobraking mission overview［J］.Journal of Spacecraft and Rockets，1999，36(3):307-313.

［13］ Smith J C，Bell J L.2001 Mars odyssey aerobraking［J］.Journal of Spacecraft and Rockets，2005，42(3):406-415.

［14］ 徐世杰.基于Lyapunov方法的空间飞行器大角度姿态机动控制［J］.宇航学报，2001，22(4):95-99.Xu S J.Large angle attitude maneuver control of spacecraft based on Lyapunov approach［J］.Journal of Astronautics，2001，22(4):95-99(in Chinese).

［15］ Mease K D，Vinh N X.Minimum-fuel aeroassisted coplanar orbit transfer using lift-modulation［J］.Journal of Guidance，Control and Dynamics，1985，8(1):134-141.