城市复杂交通网络道路重要性评估方法

张喜平，李永树，刘 刚，王 蕾

（1.西南交通大学地球科学与环境工程学院，成都610031；2.重庆邮电大学软件学院，重庆400065）

0 引言

城市路网是支撑城市区域经济和城市发展的重要基础设施。路网由许多不同的路段组成，各个路段在整个路网中所处的地理位置和承担的交通流量是不一样的，因此各个路段的重要性也有所不同。在路网中选取重要的路段对路网结构稳定性和控制有效性具有重要的意义。道路重要性的评估首要解决的问题是道路网络中路段的拓扑关系识别。GIS城市路网拓扑关系的表达有两种方式：原有拓扑与对偶拓扑结构［1－3］。在广义拓扑分析方法中，对偶图因具有拓扑关系识别简单、更能识别线路的交通特性、更符合实际交通运行特征等优势而多用于GIS的路网表达中。

目前复杂网络理论逐步应用在交通网络领域，已有很多交通网络被证实满足复杂网络特性。例如Porta等［4］应用复杂网络理论对比分析了6种具有不同结构的城市道路网络，高自友等［5］从多个角度提出复杂网络在交通领域的应用前景。各国的学者利用复杂网络理论展开了其网络节点重要性评估的研究。在路网道路重要性评估中，文献［6］提出了一种基于路段选择概率的路段重要性评估方法，该方法在考虑出行者对出行时间的感知误差的前提下，利用算法求出各个路段的选择概率，选择概率越大，路段越重要；文献［7］中提到了瑞典的学者Erik Jenalius等人提出的一种路段重要性评估算法，该方法是路网中，假设路段上已发生使路段降级甚至失效的事件，对路段失效后的后果进行计算，从而根据它确定路段的重要性；文献［8］提出了一种基于路段可靠性评价的方法用于确定路网中路段的相对重要性评估；文献［9］利用网络的连通性来反映路网中路段节点的重要性。文献［10］提出了基于场论的复杂网络节点重要性的评估方法，该方法主要计算了节点的拓扑势，根据拓扑势的计算结果决定节点的重要性，该方法考虑了复杂网络中节点的相互作用。

文献［4－9］采用直接度量或间接度量的方式去评估路段的重要性。该类研究方法虽对路网中路段重要性的评估具有一定的有效性，但对路网的流量分配要么使用最短路由的方法，要么使用用户均衡配流的方法。最短路由算法的配流方式多数以节点的介数作为节点流量的反应，这种方法通常不能真实反应节点所承载的负载量，而且介数不能体现交通拥塞对路由的影响。用户均衡配流的方法虽然能动态反应交通流量的变化，但其计算的时候通常采用一个阻抗函数作为求解的关键，该阻抗函数没有考虑节点间流量的相互影响，即假设每个节点的阻抗仅仅是该节点流量的函数。文献［10］从场论的角度提出一种复杂网络节点重要性的评估方法虽然考虑了节点间的相互作用，但没有用在交通路网中，不能体现路段的拥堵对其它路段的相互影响。

基于以上分析，本文在城市道路网络对偶图模型的基础上，提出一种基于引力场的节点重要性评估方法。该方法下，采用基于引力场的路由方法［11］进行路网的动态配流，对路段的拥堵影响定义节点的引力场，考虑了路段的拥堵影响不仅仅是由相邻路段引起的，还与相距很远的节点发生拥堵相关，并且这种影响会随着距离该路段节点的距离的增加而呈现衰减趋势。基于这种考虑，本文引入了路段节点的m阶邻居节点的概念，并用于引力场的计算中，根据节点的引力场的大小来确定路段的重要性。

1 引力场论复杂网络节点重要度评估方法

1.1 理论基础

定义1 路网对偶图［12－14］。建立基于广义路网拓扑的对偶图对偶拓扑方法是将道路按路名映射为节点、交叉口映射为边。设G＝ ｛ V ， L｝是基于广义路网拓扑建立的对偶图，其中V是网络中所有节点的集合，L为网络中所有边的集合。图1为路网拓扑图。

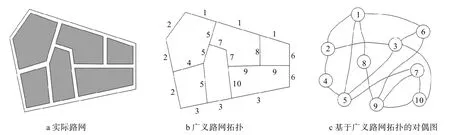
图1 路网拓扑［3］Fig.1 The road network topology

定义2 节点度值是指节点直接相连的边的数量，记为D。目前普遍认为节点的度值可以直接反映节点的重要程度。节点的度值越高，则说明该节点越重要。

定义3 m阶邻居节点。对于复杂网络G＝ ｛ V ， L｝中任意节点i（i∈V），其1阶邻居节点为与节点i之间距离为1的节点，该类节点构成的集合称作节点i的1阶邻居节点集，记为π（1）（i）；同理，则与节点i之间距离为2的节点为2阶邻居节点，其构成的集合称作节点i的2阶邻居节点集，记为π（2）（i）；如此类推，则与节点i之间距离为m的节点称为m阶邻居节点，其构成的集合称作节点i的m阶邻居节点集，记为π（m）（i）。

1.2 路网节点的引力场计算

1.2.1 节点间引力的计算

天体物理学家J.Q.Stewart研究了Newton的万有引力公式，提出了引力模型［15］。对于许多现实复杂系统，利用引力场理论研究其内部各组分之间的相互作用有助于进一步理解复杂系统的功能与结构特性，或许能发现一些重要的动力学现象。文献［11］利用节点的引力场计算，定义了节点的引力场与节点的数据传输能力成正比，与节点间的距离成反比。通过以上定义我们发现：复杂交通网络中节点的重要性与节点的数据传输能力、节点的距离、节点的度都有密切联系［16－20］。文献［11］定义的节点与数据包之间的引力考虑了复杂交通流量网络中节点的距离，节点的数据传输能力的因素，因此这种定义可以引入到交通网路中对节点重要度的评估。根据复杂交通网络中交通流量的特性，节点对之间的相互作用场与节点对的距离成反比，与节点对的数据传输能力成正比。为了模拟交通拥堵现象，为每一路段节点引入一个数据缓冲队列，用于模拟当路段出现拥堵时车辆的排队现象。根据以上分析，可以重新定义网络中任意节点对之间的引力为

式（1）可以看作节点对之间的引力方程。其中，fij为任意节点i，j之间的引力；k为常数；ci，cj为节点i和j的传输能力，即单位时间内所能处理的最大数据包个数；qi为节点i当前缓存队列中的数据包个数；qj为节点j当前缓存队列中的数据包个数，当两个缓存队列同时为0时表示节点对之间路径畅通，无拥堵现象发生；cicj／（qi＋qj）可以看作当前节点对之间的路径的畅通程度，它的取值条件是两个缓存队列不能同时为零，也就是两个路段之间存在拥堵现象。在引力场理论中，引力场中某一点所受引力与暗能量的虚拟质量和星体质量的乘积成正比，与该点到旋转中心的距离的平方成反比，且与物体的质量无关。对于复杂网络而言，节点等价于星体，而节点的传输能力等价于星体的质量，传输能力越大，则引力就越大，因此cicj／（qi＋qj）定义中，路段越拥堵路段节点之间的引力越小，反之引力越大；路段传输能力越大路段之间的引力越大；dij为节点i到节点j的最短路径长度；a和γ为两个可调节参数，分别用于调节数据传输对节点畅通程度、节点传输能力和路径长度的依赖程度，且a＞0；γ＞0。

1.2.2 节点的引力场的计算

把复杂交通网络G看作是一个包含n个节点及其相互作用的系统，每个节点周围存在一个虚拟的作用场，网络中的任何节点都将受到其他节点的联合作用，由此在整个网络拓扑上确定了一个数据场，称之为拓扑势场。真实网络的模块化与抱团特性表明：节点间的相互作用具有局域特性，每个节点的影响能力会随网络距离的增长而快速衰减。根据以上分析，引入m阶邻居节点的概念。节点的引力场不仅仅与一阶邻居节点相关还与周围从2，…，m阶的邻居节点发生关系，因此定义某个节点的引力场为一阶到m阶邻居节点与该节点的引力的和。我们引入了衰减指数函数μm作为引力计算每项取值的系数描述了引力大小随着距离的增加而衰减的趋势。路网中任意节点i的引力场计算公式为

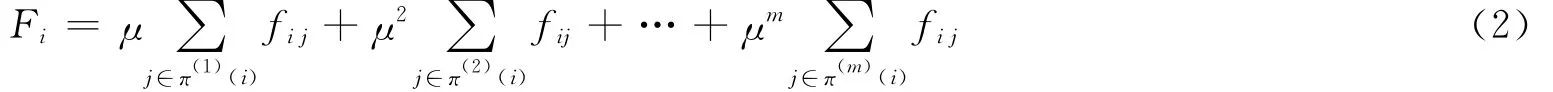
式中，Fi为节点i所激发的引力场取值，衰减指数μm，其中m取值为1，…，m，为各阶引力场的系数，原则上与节点i越相近的节点对i产生的引力场越大，与i相距越远的节点对i产生的引力越小，因此系数项取值0≤μ≤1。随着距离阶数的增加，系数项取值越小，这表明了距离阶越大对节点i产生的引力越小。

1.3 路网节点重要度评估方法

网络中的任何节点都将受到其他节点的联合作用。因此，节点的重要度不仅与一阶邻居节点相关，还与网络中所有的节点相关。定义路段重要度评估函数为

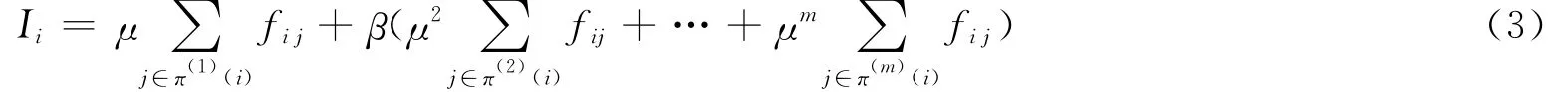
该评估函数中，当β＝0时，评估函数的评估结果只与一阶节点相关，因此评估结果等价于基于度的评估结果；而β的取值满足0＜β≤1时，该系数的取值直接代表了二阶以上的节点对节点重要度的贡献，我们将在实验结果中讨论β的取值对重要度的排序结果的影响。

已知GIS复杂路网，所考察邻居节点深度为m，根据以上分析我们提出评估路段节点重要度的具体算法为：1）从GIS路网结构图映射出对偶拓扑结构：G＝ ｛ V ， L｝。V是路网的顶点集合，也是路网的路段集合。L是路网的边的集合，也是路网的交叉路口的集合。2）根据对偶拓扑结构，提取任意节点i的1到m阶邻居节点集：π（1）（i），π（2）（i），…，π（m）（i）；3）根据引力场路由算法为路网动态配流。4）计算节点i的各阶邻居节点集的每个阶的引力和：确定节点i的引力场Fi； 5）根据式（3）计算每个节点的重要度，输出Ii。

2 试验与仿真

2.1 城市交通路网关键道路提取以及路网的配流

根据成都市城区2007年街道详图，按路名提取197个路段，构建原始广义路网拓扑。基于该路网结构，采用对偶拓扑方法以道路为节点、交叉口为边构建路网对偶图。为了能够较好地描述路网的整体结构和复杂性，将本文的路段重要性评估方法引入到路网关键道路提取中，修改文献［13］算法为路网对偶图提取10条关键道路如图2所示。

传统均衡配流是从全局流量分布的角度实行路段交通流的动态分配，缺乏对人们交通出行认知知识的考虑。从行为认知学角度，人们的空间行为由类似于万有引力定律的规律所决定［21］，故人们的交通出行行为也应可以用引力模型来描述。所以，为得到更符合实际的交通模拟结果，本文的路网配流方法采用文献［11］中的引力场路由方法，具体方法如下：假设在给定的复杂网络上，每个节点都具有如下的功能：路由、接收数据包、发送数据包。网络的初始负载为0，每一个时间步t会产生r个数据包。这些数据包在网络中传输会随机地选择源节点与目标节点。产生的数据包自动地添加到源节点的数据包缓存队列的尾部，在单位时间步内每个节点最多能发送ci个数据包，节点的缓存队列长度无限且采用先进先出方式。在网络传输过程中，数据包总是由当前节点发送给某个邻居节点，若该邻居节点为数据包的目标节点，则删除该数据包；否则，按照引力场路由选择策略进入该邻居节点的缓存队列。

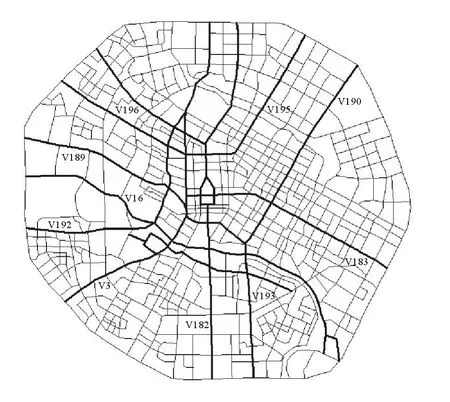
图2 关键道路图Fig.2 Key road map

2.2 试验结果仿真分析

为了验证本文算法的有效性，根据本文的计算方法，采用引力场路由的策略为路网进行配流，得到了路网的拥堵与非拥堵的临界状态负载的取值Rc＝12。在空闲状态，路网非拥堵取R＝6，即R＜Rc；在最大临界状态，路网处于拥堵与非拥堵的临界值，取R＝12，即R＝Rc；在拥堵状态，取R＝20，即R＞Rc，3种状态下的交通流数计算出了197个路段节点的引力场的取值，根据图2提取的关键道路选择：V182，V190，V192，V195，V183，V16，V3，V189，V196，V193这条关键道路作为仿真分析结果的评估。

表1为10条关键道路在路网处于空闲状态、临界状态以及拥堵状态下的引力情况。在空闲状态下，各节点缓存队列中数据包数为0，各个节点的引力场重要度排序结果与基于节点度的方法比较接近，其原因是公式（1）在节点缓存队列为0时，度越大的节点其引力作用越大；而在临界状态与拥堵状态下节点的重要度排序结果都与基于节点度的评价方法存在明显差别。随着负载量的增加，各节点缓存队列中数据包数不再为0，且节点的拥堵程度与其缓存队列中数据包数基本成正比关系。根据公式（1）可知，节点越拥堵，节点间的引力就越小，那么公式（2）所计算的节点引力场值也越小。根据表2可以看出：当R＝6时最重要路段为182号，随着182号路段拥堵增加到临界状态，当R＝12时，16号路段是最重要的路段，而182号路段排序在最后，这说明182号路段的拥堵程度在10个节点中最严重。而当R＝20时候，路网陷入全面拥堵状态，这时193号路段最重要，而182号路段依旧是最拥堵的路段。由此表明：1）拥堵可以改变路段在路网中的重要程度；2）在空闲状态下，路段的重要性取决于路段的结构特性，即度、中心性等；3）在拥堵状态下，从行为认知学角度，越拥堵的路段由于其已经汇聚了大量交通流，在路段拥堵没有得到一定缓解的情况下，该路段对其他交通流的吸引力将下降，进而降低了该路段在路网中的重要程度。故本文的节点重要度研究方法能实时反映路段的拥堵状况，出行者可以根据节点重要度的排序结果选择出行的路径。

表1 路网关键道路节点引力场、度、介数Tab.1 Indices of gravitational field degree betweenness in road network’s key road node

表2 路网关键道路节点重要度评价结果（降序）Tab.2 Node importance evaluation results in road network′s key road node

由图3可以看出，节点重要度评估结果与m的取值密切相关。理论上，m的取值满足 ［ 0，D ］区间。为进一步分析m为何值时本文评估方法可得到准确的评估结果，分别在路网的不同负载下研究了节点重要度随m的变化情况。如图3所示，a，b，c分别给出了路网中10个关键道路节点在R＝6无拥堵状态、R＝12拥堵与非拥堵临界状态、R＝20完全拥堵状态3种情况下重要度与m值的关系。由仿真结果可知，节点重要度评估结果随m值的增大总体呈现“由不稳定到稳定”的变化趋势，且当m小于网络平均路径长度L时（即m＜L），节点重要度I随m的增加变化较大，为不稳定状态；而当m大于网络平均路径长度L（即m＞L），节点重要度I随m值的持续增加几乎不再变化，节点的重要度评估结果进入稳定状态（仿真中L的取值为5）。由此，可以得出一个重要结论：只要考察的邻居节点深度m值大于网络的平均路径长度L，本文评估方法便能得到准确、可靠及高精度的评估结果。

图3 节点重要度与m值的关系Fig.3 Relationship between value of mand node importance

由公式（2）和（3）可知，μ用于衡量节点引力场随距离的衰减趋势，故取值满足0≤μ≤1；β用于评估二阶以上节点对当前节点重要度的贡献，从空间自相关可知，节点自身属性对其重要性的贡献程度应大于其他节点对该节点的影响，故β取值应满足0≤β≤1。故可以通过调节μ，β的取值组合分析节点引力场对多阶邻居节点及自身特性的敏感程度。为进一步检验本文方法的有效性，对不同μ，β取值下路段的引力场情况及重要程度进行仿真。实验数据表明：在非拥堵状态和拥堵临界状态下μ，β的取值对节点重要度的排序没有影响，而在拥堵状态下μ，β的取值对重要度的排序有影响。表3是在拥堵状态下μ，β的取值与关键路径节点引力场的取值关系图，仿真中令m＝3，R＝12。表4是表3的关键路径节点重要度的排序结果。由引力场的定义可知，拥堵会使引力场的取值减小。随着拥堵的增加路网中很多节点引力场的取值趋向于0或为0。表3的第一列数据恰好印证了这一定义。引力场取值为0的节点（路段182，190，192，16，3）用于重要度排序中不能得出正确的排序结果，在表4中μ＝0.2的时候，最后5个节点的重要度排序是不准确的，随着μ的取值的增加表4中最后5个节点的重要度排序能得出精确的结果。而当β＝0.2时，表3的第2列数据有4个节点的引力场取值相同（190，192，16，3），在表4中这4个节点的重要度排序结果也是不正确的，随着β值的增加，在表4的最后两列能得到精确的节点重要度的排序结果。

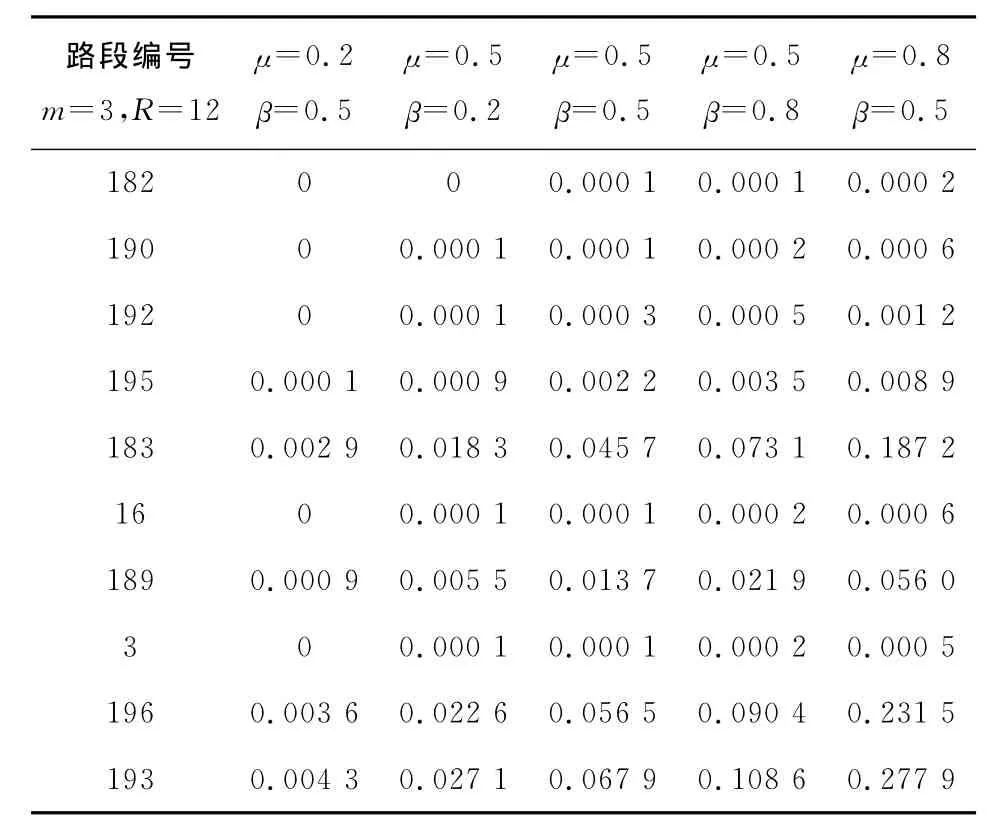
表3 拥堵状态下μ，β取值与关键路径节点引力场关系Tab.3 Relationship between the values ofμ，βand nodes in the key road of gravitational field in the state of congestion

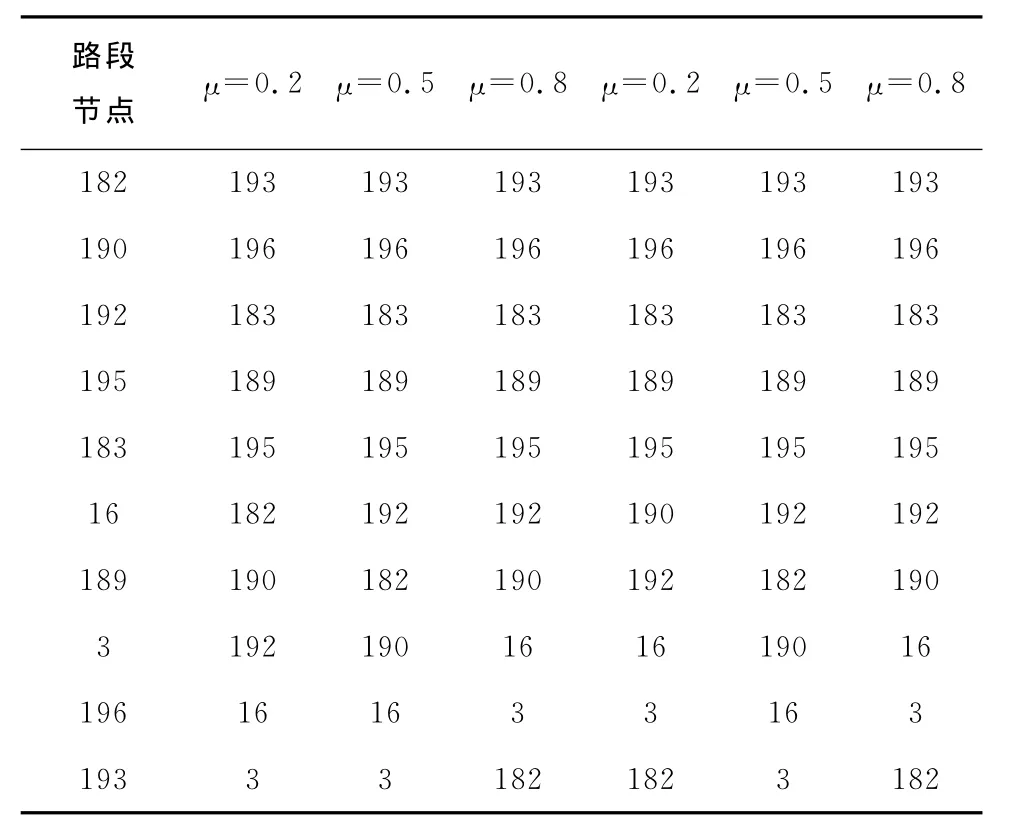
表4 拥堵状态关键路径节点重要度排序结果（降序）Tab.4 Key road node importance ranking results in the state of congestion

3 结论

对路网中道路重要性的动态、快速、准确的评价对交通计划、控制和指挥服务有着重要的意义。目前道路重要性评估中的主要困难是难以采用动态的方法准确地接近实际地模拟路网的实际运行情况。本文研究的基于场论的城市道路重要性评估方法采用动态的路网配流技术，在路段引力场的定义中模拟了路段的拥堵排队现象，使最后的路段评估模型能动态体现路段的拥堵状况。实验结果表明：本文的评估方法能进一步揭示复杂路网中的拥堵节点对重要性的影响。通过在评估模型中定义参数μ，β调节了路段节点引力场的取值，解决了评估函数在取相同值的时候无法得出正确的评估结果的问题。本文的评估模型能够帮助人们理解路网上路段在拥堵下的重要性的依赖关系，为发现复杂路网的关键路径节点提供了一种新的研究思路。

［1］ 李清泉，曾喆，杨必胜，等.城市道路网络的中介中心性分析［J］.武汉大学学报（信息科学版），2010，35（1）：37－41.Li Qingquan，Zheng Zhe，Yang Bisheng，et al.Betweenness centrality analysis for urban road networks［J］.Geomatics and Information Science of Wuhan University，2010，35（1）：37－41.

［2］ 郑年波，陆锋，段滢滢.道路转向延迟的动态对偶图模型［J］.中国图象图形学报，2010，（6）：915－920.Zheng Nianbo，Lu Feng，DuanYingying.Dynamic dual graph mode for turn delays on road networks［J］.Journal of Image and Graphics，2010，（6）：915－920.

［3］ 刘刚，李永树，杨骏，等.对偶图节点重要度的道路网自动选取方法［J］.测绘学报，2014，43（1）：97－104.Liu Gang，Li Yongshu，Yang Jun，et al.Auto－selection method of road networks based on evaluation of node importance for dual graph［J］.Acta Geodaetica et Cartographica Sinica，2014，43（1）：97－104.

［4］Port A S，Crucitt I P，Latora V.The network analysis of ur ban streets：a dual approach［J］.Physica A，2006，369（2）：853－866.

［5］ 高自友，吴建军，毛保华，等.交通运输网络复杂性及其相关问题的研究［J］.交通运输系统工程与信息，2005，5（2）：79－83.Gao Ziyou，Wu Jianjun，Mao Baohua，et al.Study on the complexity of traffic networks and related problems［J］.Journal of Transportation Systems Engineering and Information Technology，2005，5（2）：79－83.

［6］ Michael A P T.Applying interactive color graphics in traffic planning［J］.Computers ＆ Graphics，2007，11（3）：241－248.

［7］ 王晓丽，温冬梅，张利分.交通网络重要路段确定方法研究［J］.山西科技，2007，（1）：91－95.Wang Xiaoli，Wen Dongmeng，Zhang Lifen.Study on the method of defining important sections of the traffic network［J］.Shanxi Science and Technology.2007，（1）：91－95.

［8］ 侯立文，蒋馥.城市道路网中路段相对重要性研究［J］.系统工程理论方法与应用，2004，13（5）：623－627.Hou Liwen，Jiang Fu.Study on the relative importance of links in urban roads network［J］.Systems Engneering Theory Methodology Applications，2004，13（5）：623－627.

［9］ 刘思峰，万寿庆，陆志鹏，等.复杂交通网络中救援点与事故点间的路段重要性评价模型研究［J］.中国管理科学，2009，17（1）：119－124.Liu Sifeng，Wan Shouqing，Lu Zhipeng，et al.The importance of highway section evaluation model in complex network between accident point and rescue point in the emergency situations［J］.Chinese Journal of Management Science，2009，17（1）：119－124.

［10］赫南，淦文燕，李德毅，等.一种基于数据场的网络节点重要性度量方法［C］／／中国人工智能学会第12届全国学术年会论文汇编.哈尔滨：哈尔滨工业大学出版社，2009：55－60.He Nan，Gan Wenyan，Li Deyi，et al.Evaluate nodes importance in the network based on data field theory［C］／／Chinese Artificial Intelligence Society of the Twelfth National Academic ConferenceProceedings.Harbin：Harbin Institute of Technology press，2009：55－60.

［11］刘刚，李永树.基于引力场理论的复杂网络路由选择策略研究［J］.物理学报，2012，61（24）：248901.Liu Gang，Li Yongshu.Routing strategy for complex networks based on gravitation field theory［J］.Acta Phys Sin，2012，61（24）：248901.

［12］李玉兰，李耀堂.城市道路网容量的对偶图算法［J］.云南大学学报（自然科学版），2006，（4）：293－297.Li Yulan，Li Yaotang.Dual graph algorithm for the volume of the city road network［J］.Journal of Yunnan University，2006，（4）：293－297.

［13］徐英睿，陆锋，张洪岩.基于对偶图的城市交叉口延误分析［J］.公路，2012，（9）：149－153.Xu Yingrui，Lu Feng，Zhang Hongyan.Based on the dual graph analysis of the urban intersection delay［J］.Highway，2012，（9）：149－153.

［14］闫文彩，张玉林，赵茂先，等.基于复杂网络的城市路网可靠性分析［J］.山东科学，2011，（2）：65－70.Yan Wencai，Zhang Yulin，Zhao Maoxian，et al.Complex network based reliability analysis of urban road networks［J］.Shangdong Science，2011，（2）：65－70.

［15］James P E，Martin G J.地理学思想史［M］.李旭旦，译.北京：商务印书馆.1989：481－482.

［16］Restrepo J R，Ott E，Hunt B R.Characterizing the dynamical importance of network nodes and links［J］.Phys Rev Lett，2006，97（9）：094102.

［17］Barthelemy M.Betweenness centrality in large complex networks［J］.Eur Phys J B，2004，38（2）：163－168.

［18］Lohmann G，Margulies D S，Horstmann A，et al.Eigenvector centrality mapping for analyzing connectivity patterns in fMRI data of the human brain［J］.PloS ONE，2010，5（4）：e10232.

［19］Jin J，Xu K，Xiong N，et al.Multi－index evaluation algorithm based on principal component analysis for node importance in complex networks［J］.IET Networks，2012，1（3）：108－122.

［20］Zhang J，Xu X K，Li P，et al.Node importance for dynamical process on networks：a multiscale characterization［J］.Chaos，2011，21（1）：016107.

［21］田志文，周海涛.引力模型预测交通分布量的误差分析［J］.公路交通科技，1994，11（2）：47－51.Tian Zhiwen，Zhou Haitao.The error analysis of traffic distribution by gravity model［J］.Joural of Highway and Transportation Research and Development，1994，11（2）：47－51.