球形传声器阵列脉冲响应测量的非线性失真分析*

刘昱 谢菠荪 麦海明 陈嘉衍

(华南理工大学 物理系 声学研究所，广东 广州510640)

球形传声器阵列测量是一种新型的室内声学分析技术.与传统的单传声器测量相比较，其利用球面上分布的多个传声器测量声场空间脉冲响应，并通过波束形成等信号处理方法，分析直达声和早期反射声的入射角度等参数，获取室内声场更多的空间信息［1-2］.

利用球形传声器阵列测量声场空间脉冲响应的原理和一般声学系统的脉冲响应或传输函数测量(如单通路房间脉冲响应测量，头相关传输函数测量［3］)相类似.通过特定的声源和信号激发产生室内或环境声场，并用传声器阵列接收，所得到的阵列上各个传声器的脉冲响应即声场的空间脉冲响应.脉冲响应测量的准确性与激发声源及信号的性质以及后续信号处理方法等因素有关.空间声场脉冲响应的测量方法有许多种，如早期的脉冲法，但这类方法存在测量重复性差等问题.为了满足测量精确性和重复性等一系列要求，目前主要是采用功率放大器和扬声器组成的电声激发声源系统［4］，以及采用以最大长度序列(MLS)为代表的伪随机噪声信号和以正弦对数扫频(下文简称对数扫频)的扫频信号作为激发信号.总体上，MLS 是一种确定的周期信号，同时具有类似白噪声的统计特性，利用多次测量平均能得到较好的抗噪能力，但容易受系统非线性失真的影响.对数扫频信号是一种瞬时频率随着时间变化的信号，有较好的抗非线性失真能力.激励声源以及相应信号处理方法各有特点，许多研究对这些激励声源进行了比较，给出了使用这两种激励声源测量方法的适用条件［4-5］.

影响脉冲响应测量的因素主要包括环境噪声、非线性失真和时变失真等，许多研究工作分析了这些因素的影响，从而比较不同测量方法的性能［4，6-8］.但是这些工作主要基于单传声器捡拾的测量条件，通常忽略传声器装置的几何形状散射对测量信号的影响.传声器阵列等测量设备的出现，使得传声器装置的散射对测量的影响不可忽略.球形传声器阵列作为一种常用的传声器阵列，其特殊的几何结构便于理论计算，并和实际测量结果比较，进而分析传声器阵列散射对测量脉冲响应的影响.由于球体表面对入射声波产生的散射作用，球面受声点的频域响应和受声点相对于声源的位置有关.对特定的声源位置，声源的非线性失真对不同位置的传声器输出的影响是不同的.目前还未见有关声源非线性失真对球形传声器阵列脉冲响应影响的研究报道.文中将以典型的球形传声器阵列传声器布置为例，分析MLS 方法和对数扫频法两种测量方法的非线性失真影响.

1 脉冲响应或传输函数的测量原理

1.1 最大长度序列法

最大长度序列是常用的测量激励信号之一，是一系列-1 或1 组成的周期性伪随机二进制序列(包括电平移动)［9］.通过串联M 个移位寄存器以及异或门组成的反馈电路，在时钟脉冲的控制下，输出周期最大长度为L =2M-1 的序列，称之为M 阶的MLS.MLS 信号拥有优秀的自相关特性，对于周期长度为L 的MLS 信号，其归一化循环自相关系数可表示为

当MLS 信号通过一个线性时不变(LTI)系统，利用输入信号x(n)与输出信号y(n)做归一化循环互相关，可得:

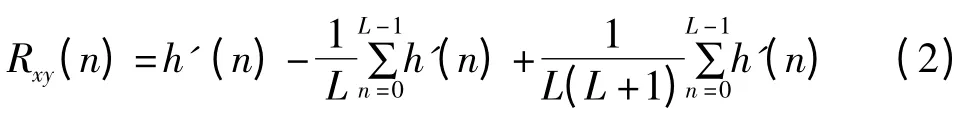
式中，h'(n)是系统周期脉冲响应，阶数M 越大，周期长度L 越长，归一化循环互相关系数Rxy(n)越接近h'(n)，因此可计算Rxy(n)作为系统脉冲响应h(n)的有效估计.MLS 方法假定待测系统为线性时不变系统，当系统不满足上述条件，将引起不同程度的失真.

1.2 对数扫频信号法

正弦扫频信号是一种瞬时频率随着时间连续变化的信号，对非线性失真有较好的抗干扰能力，常用于电声器件测量.常用的正弦扫频信号主要包括线性扫频信号和对数扫频信号两种类型，其中对数扫频信号拥有更好的抗噪能力［10］.

对数扫频信号的瞬时频率随时间以指数增长，假设其时域表达为x(t)，长度为T，当给定角频率的上限和下限ω1和ω2，可得到瞬时角频率ω(t)表达式:

通过对ω(t)积分，可求出相位关于时间的函数:

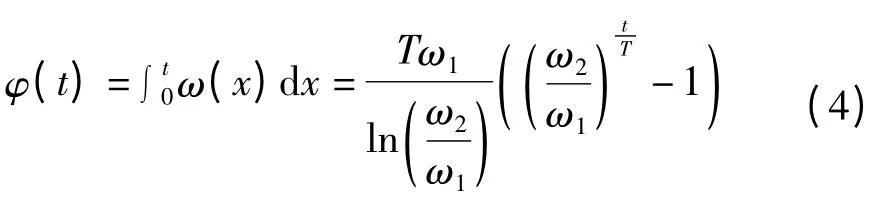
从而得到信号:

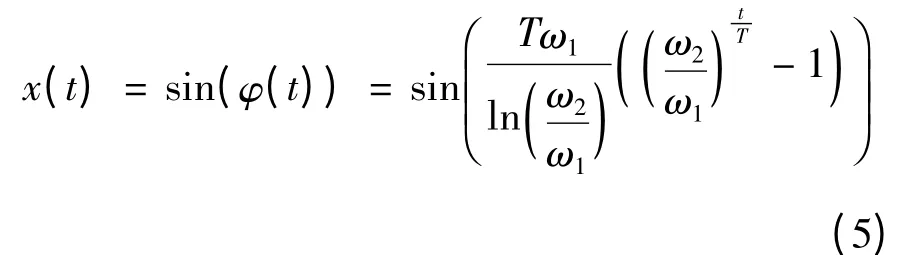
使用时间反转滤波技术，已知输入输出信号可求解系统的传输函数.假定系统传输函数的脉冲响应为h(t)，输入信号为x(t)，输出为y(t)，对应其频率响应为H(f)、X(f)、Y(f).对输入信号做时间反转变换得到x(-t)后与输出信号y(t)做线性卷积，得到:

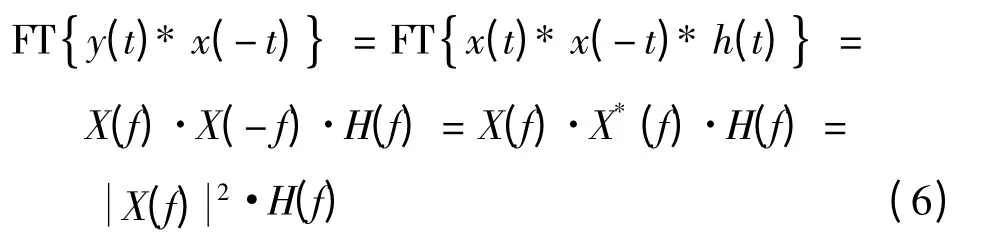
式中，FT{}表示傅立叶变换，*表示共轭，因此有:

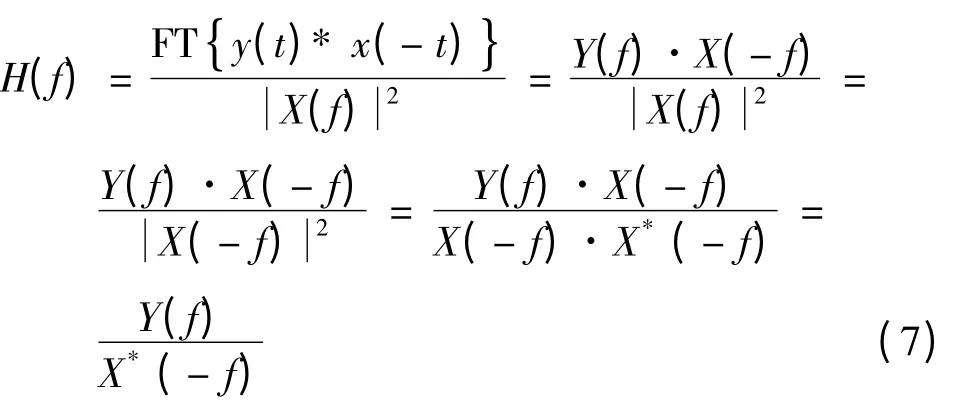
对H(f)做傅里叶逆变换即可求出系统脉冲响应h(t).为了消除信号处理中的吉布斯效应，通常信号的开始和结束部分需作淡入和淡出处理.

2 球形传声器阵列测量的分析方法

一般电声系统测量可以简化为图1所示模型.声源(扬声器)系统由线性脉冲响应ha［n］和一个无记忆的非线性系统表示，由环境和测量装置等反射构成的待测系统表示为线性脉冲响应hb［n］的线性时不变系统(忽略测量仪器产生的非线性失真).在自由场条件下使用球形传声器阵列测量时，hb［n］为球形传声器阵列的传输函数，当球形传声器阵列可看作实心刚球时，可用刚球散射模型计算近似获取.因此，球形传声器阵列脉冲响应的非线性失真分析实质是考虑一个非线性失真子系统和刚球散射模型构成的线性子系统对测量脉冲响应产生的影响.而且因为系统中非线性变换对过去输入通常没有“记忆作用”，故可看作是一个无记忆非线性子系统.这种无记忆的非线性子系统和线性子系统的串联形式构成了一个Hammerstein 模型非线性系统［11］.通过适当地设定Hammerstein 模型中非线性系统的参数，可以模拟得到与实际测量相近的结果，进而分析非线性失真在测量中产生的影响.

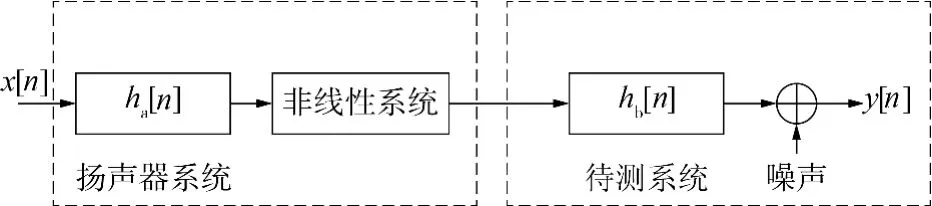
图1 电声系统测量模型Fig.1 Model of measurement by electroacoustic system

2.1 仿真方法

2.1.1 非线性失真系统

非线性问题复杂多变，电声系统中常见的非线性失真有谐波失真和互调失真等不同类型，无记忆的非线性系统输出u(t)可以用多项式形式近似表示［12-13］

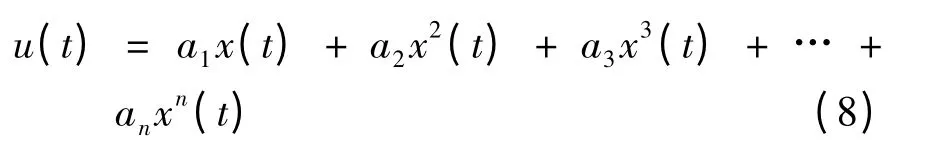
式中，x(t)为输入信号，an为n 阶非线性阶次的系数.通常在电声系统测量中，随着阶次增大，非线性失真将逐步减小，因此仿真中假定an随阶数指数下降:

式(9)中p 为仿真的参数，用以产生不同程度的非线性失真.图2显示600 和1000Hz 纯音组成的输入信号在非线性系统于p =3 和p =6 时的仿真结果.

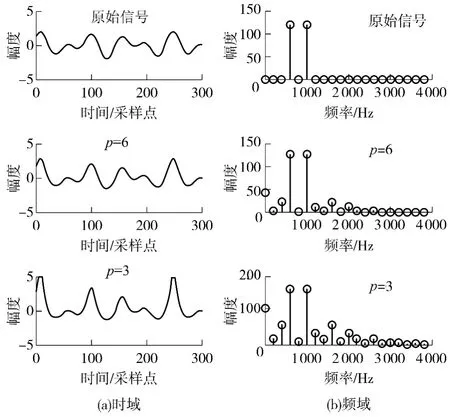
图2 纯音信号的非线性失真Fig.2 Non-linear distortion of pure tones

2.1.2 刚球模型

考虑实际几何形状以及表面声学阻抗，文中所使用的球形传声器阵列可看作一个刚性球体(见图3(a)).传声器在球面上分布已知，见图3(b).因此，声源传播至球面的过程可视为一个线性时不变系统.对任意方向平面波入射，受声点处的声压可表达为［14］

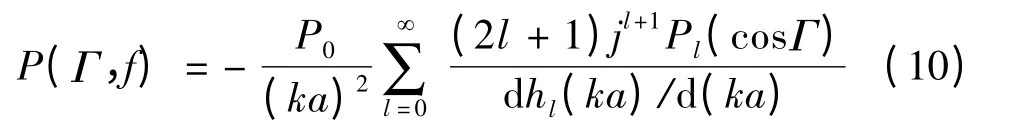
式中，P0为入射平面波的声压振幅，Γ 为入射声波与圆心指向受声点联线的夹角，k 为波数，Pl(cosΓ)为l 阶勒让德多项式，dhl(ka)/d(ka)为l 阶第二类球汉克尔函数的一阶导数.

图3 球形传声器阵列以及球面传声分布Fig.3 Spherical microphone array and distribution of microphones on the sphere

球面上的声压与球半径、受声点相对声源位置以及频率有关.为了与实际测量结果比较，取球半径与实际球形传声器阵列半径一致，即a =0.0975 m，并选择了与实际阵列中一致的传声器分布.球面上不同入射夹角的受声点传输函数幅度谱见图4.

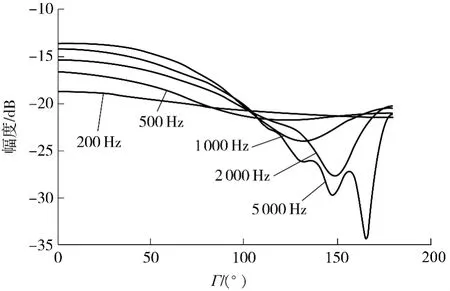
图4 不同频率下刚球模型传输函数的幅度谱Fig.4 Magnitude of rigid sphere model transfer function in different frequency

2.2 评价指标

为了评价仿真结果的性能，给出了以下常用的价指标:

(1)总谐波失真(THD).其定义为所有谐波成分功率之和与基频信号功率的比值，常用于评价信号非线性失真的程度.

(2)峰值信噪比(PSNR).PSNR 可较为全面地描述MLS 信号在低信噪比下的性能［12］，其定义为

式中，hpeak为理想脉冲响应h(t)的峰值.

(3)信噪比(SNR).选取脉冲信号能量与脉冲信号尾部能量之比作为信噪比的估计［4］.上述信噪比估计与理想信噪比结果有一定的出入，但是易于比较仿真和实际测量的结果.为了提升信号的信噪比，两种测量方法均使用时间窗截断方式消除主脉冲外的误差噪声.

3 仿真结果

仿真分为两部分，第1 部分仿真单传声器下，两种测量方法在非线性失真发生器作用下的结果，第2部分利用刚球散射模型，仿真非线性失真在球面上的变化.MLS 信号选用17 阶共131071 点的MLS 信号，在采样率为48000 Hz 下长度为2.73s.对数扫频信号采样率为48000 Hz 的3 s 信号，频率上、下限分别为22 和24 000 Hz，信号开始和末尾使用汉宁窗作0.05 s 的淡入淡出处理.

3.1 单传声器测量的非线性失真分析

单传声器测量条件下，可直接观察无球面散射下非线性失真对测量结果的影响.利用2.1.1 节的非线性失真发生器，仿真不同程度非线性失真干扰下(基频1000Hz 时，THD 分别为0%，0.45%和1.1%)的测量结果，结果显示MLS 法和对数扫频法抗非线性失真能力差异明显.在不产生非线性失真的情况下(THD 为0%)，两种测量方法获得的脉冲信号都有足够高的信噪比(大于100 dB).当引入非线性失真后，两种测量方法的峰值信噪比和信噪比均有不同程度的下降(MLS 法的PNSR =9 dB，SNR =26 dB;对数扫频法的PNSR=24 dB，SNR=34 dB).但在相同非线性失真干扰下，MLS 方法的测量精度损失要远高于对数扫频法(见图5，峰值为1.18).随着非线性失真进一步增大(THD 为1.1%)，MLS 方法的测量性能急剧下降(PNSR= -8dB，SNR=15.8 dB).同时，非线性失真产生的干扰分布在MLS 法测量的脉冲响应周期内［12］.相比之下，使用扫频信号测量(PNSR=16 dB，SNR=28 dB)，由谐波失真产生多次谐波成分分布在脉冲的非因果部分(见图6，峰值为1.18).这是由于对数扫频法中的不同阶次的频率成分经过时间反转处理后造成的，其在脉冲响应时间轴上的偏移位置ΔtN满足［15］:

式中，T 为对数扫频信号时间长度，ω1、ω2为角频率上限和下限，N 为阶次.

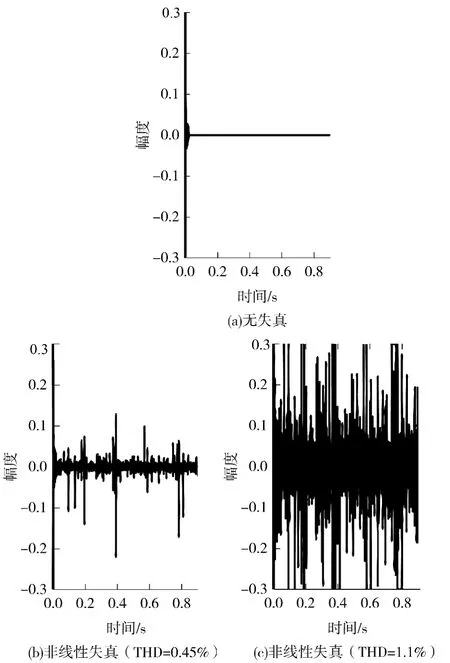
图5 MLS 方法在不同非线性失真条件下的脉冲响应Fig.5 Impulse response in non-linear distortion measured by MLS method

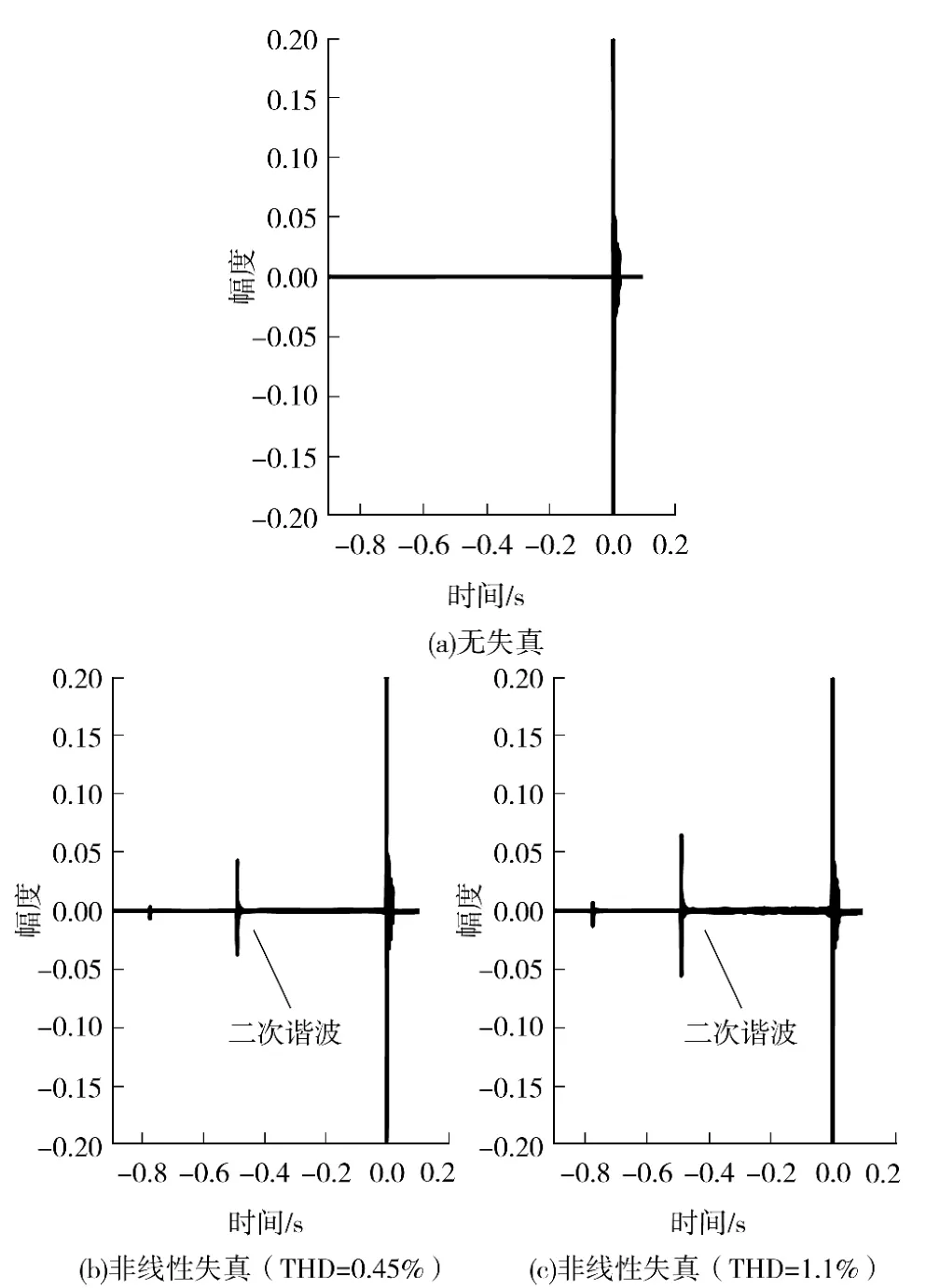
图6 对数扫频方法不同时非线性失真条件下的脉冲响应Fig.6 Impulse response in non-linear distortion measured by sweep method

3.2 球形传声器阵列检拾的非线性失真分析

用刚球模型模拟传声器阵列对入射声波的散射.利用自由场条件下的入射平面波(也就是单传声器测量的信号)，经过由刚球模型构成的线性滤波器，可分析球面散射引起的期望声压成分和非线性失真成分的变化.在文中，分别以200、500、1000 和5000Hz 4 个单频的期望声压(纯音)信号代入刚球模型计算，图7给出球面上单个传声器检拾到信号总谐波失真与声波入射角的关系.结果表明，总谐波失真取决于入射声波相对于受声点的位置，刚球模型滤波器对非线性失真有放大或者衰减的作用.球面上面对声波入射方向的传声器，其测量信号的THD 将略微高于单传声器测量信号，而背对声源入射方向的传声器，由于球体阴影作用导致的高频信号衰减，使得总谐波失真降低.实际单传声器的总谐波失真测量结果验证了仿真结果的有效性，但受环境声反射和传声器阵列的电声性能影响，与仿真结果略有偏差.基频信号为200Hz 时，球面上最小THD 位置点出现在夹角130°左右，随着基频信号频率提高，最小THD 位置点将向正背面迁移.由于现实中扬声器的非线性失真特性，低频信号产生的总谐波失真(扬声器实际测量THD 为3.15%，基频为100 Hz)要远高于高频(扬声器实际测量THD 为0.07%，基频为5000 Hz)，意味着低频产生的非线性失真影响将更明显，球面实际的非线性失真分布可能主要取决于低频信号的非线性变化.

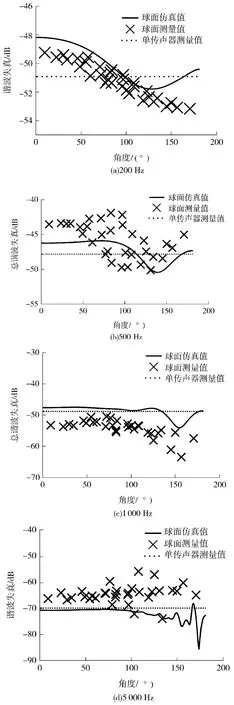
图7 球面上纯音信号的总谐波失真与入射角的关系Fig.7 Relation between THD and incidence angle of pure tones on the sphere

3.3 讨论

当声源面对刚球表面传声器时，刚球对高频声波的近似反射作用，使传声器接收到的高频声压提高大约6 dB［16］.当声源背对刚球表面传声器时，刚球对高频声波的阴影作用，使传声器接收到的高频声压明显衰减.对半径为0.1 m 的球，对大约3 kHz 以上高频声波起明显作用.值得注意的是，根据式(10)，刚球散射模型的频率响应与球半径及传声器位置有关，文中为了与实际测量对应，仿真中设置球半径为0.0975 m，并选择了与实际传声器阵列一致的传声器分布.当取不同球半径以及传声器分布时，其定量结果也有所不同，但是并不影响上述定性结论.

在球形传声器阵列输出的波束形成算法中，面对刚球表面传声器输出的贡献最大，因此声源的非线性失真对波束形成的影响将变得明显.因此，仿真结果表明，球形阵列传声器阵列的传输函数测量采用抗非线性失真能力更强的对数扫频法更佳.

4 测量验证

利用扬声器系统和球形传声器阵列组成的测量系统，比较MLS 法以及对数扫频法实际测量性能，并验证仿真结果.测量设备主要包括:B＆K 定制64 通路球形传声器阵列以及采集系统，RME fireface UC 音频接口，KEF LS50 同轴扬声器，具体布置见图8.测量场地为华南理工大学建筑声学实验室的半消声室，为了进一步消除地面反射的影响，在传声器阵列四周的地面上铺设了吸声材料，满足近似自由场环境.阵列支撑杆的半径为0.015 m，与球形传声器阵列相比(半径为0.0975 m)，反射影响较小.

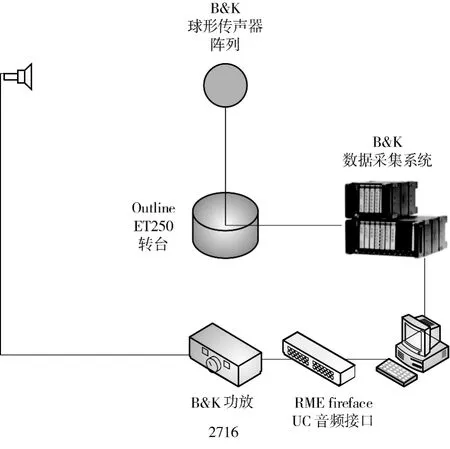
图8 测量系统布置Fig.8 Setup of measure system

图9(a)和图9(b)给出了使用对数扫频法和MLS 法的实际测量结果.结果证实了3.1 节的结论，在相同扬声器非线性失真的条件下，MLS 法测得脉冲响应的信噪比大约为23 dB 左右，要远小于对数扫频法45 dB 信噪比.同时测量结果显示使用两种测量方法测量得到的脉冲响应信噪比随着入射夹角呈相反的变化趋势.对数扫频法测量结果体现整体信号强度对信噪比的作用(图10(c)显示了传声器接受信号强度随着入射夹角衰减)，面向声源的传声器拥有最高的信噪比，并随着受声点转向背对声源方向，信噪比逐渐降低，最大最小信噪比相差约20 dB，MLS 法测量结果则随着入射夹角增大，信噪比小幅度提高.根据3.2 节的结论，球面散射的作用，使得背对声源表面接收点信号的非线性失真程度降低，是球面上MLS 信号测量结果信噪比显示相反趋势的主要原因.图10(b)结果同样显示，在无法保证扬声器系统非线性失真足够小的情况下，提高测量信号强度，对改善MLS 测量结果信噪比作用较小.

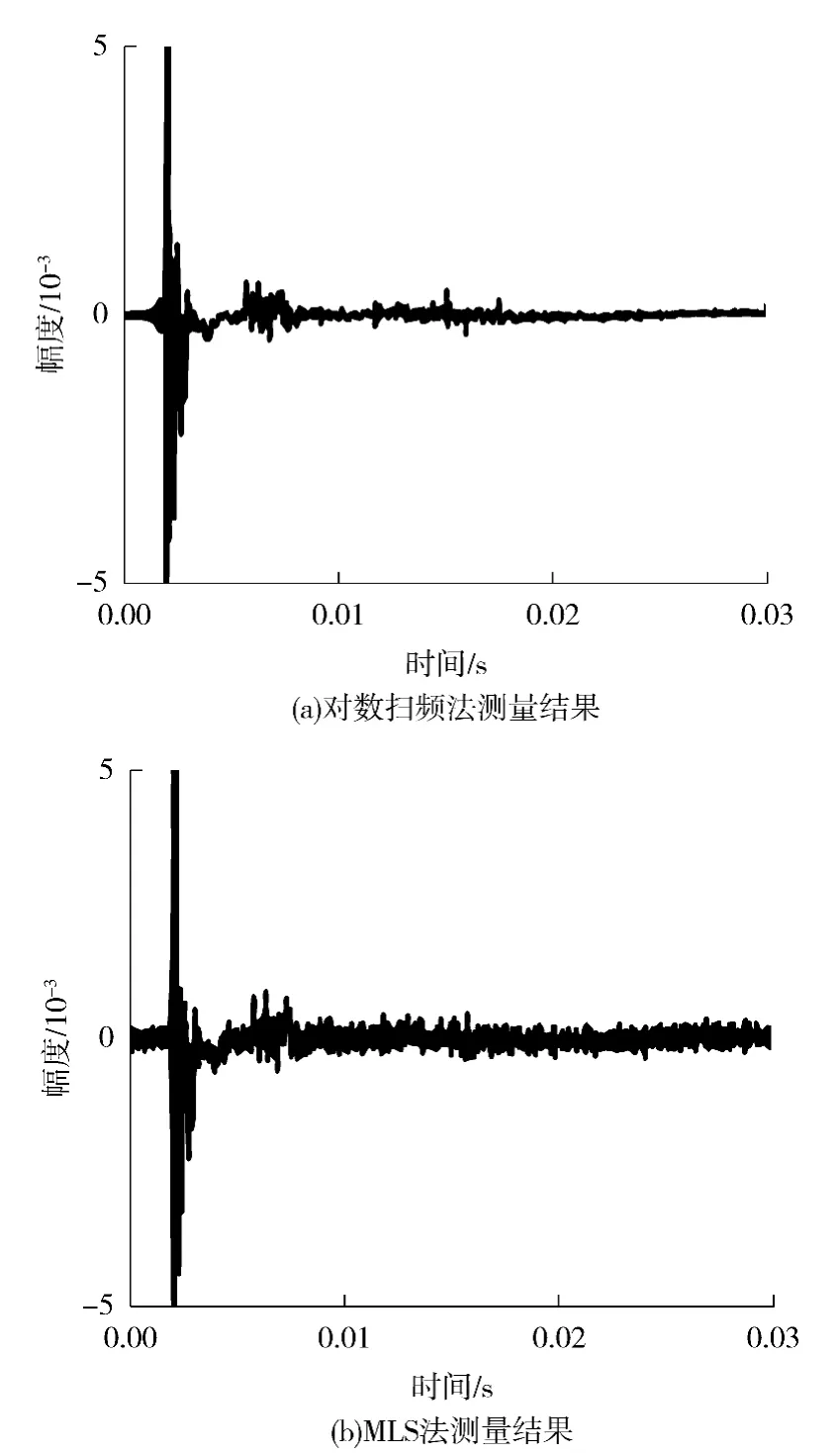
图9 正对声源入射方向受声点处的脉冲响应Fig.9 Impulse response of receiver against sound source

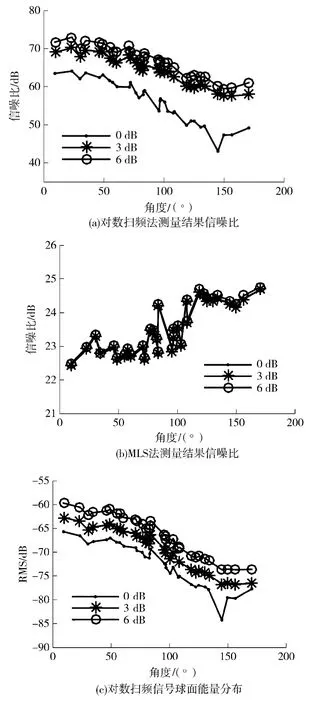
图10 两种方法测量结果的信噪比和球形传声器能量分布Fig.10 SNR of results measured by two methods and RMS distribution on the sphere

5 结论

文中利用仿真和实际测量，分析了在刚性球形传声器阵列测量中，非线性失真对两种常用脉冲响应测量方法的影响，提出了一种对非线性失真评估方案.由于刚性球面对声波的散射作用与频率有关，传声器检拾得到的谐波成分以及谐波失真将因入射声波角度而发生变化.

总谐波失真在背对声源的受声点位置较正面低.这个结果表明，取决于受声点的位置，测量器件几何形状可对信号非线性失真有放大或衰减的作用.这种特性将较大程度干扰对非线性失真更敏感的测量方法(如MLS 法)的测量结果，而对对数扫频法影响较小.

总体而言，对数扫频方法较MLS 法有更好的抗非线性失真能力，更适合球形传声器阵列脉冲响应测量.

［1］Khaykin D，Rafaely B.Acoustic analysis by spherical microphone array processing of room impulse responses［J］.J Acoust Soc Am，2012，132(1):261-270.

［2］Huleihel N，Rafaely B.Spherical array processing for acoustic analysis using room impulse responses and timedomain smoothing［J］.J Acoust Soc Am，2013，133(6):3995-4007.

［3］Xie B.Head-related transfer function and virtual auditory display［M］.United States:J Ross Pub，2013.

［4］Stan G，Embrechts J，Archambeau D.Comparison of different impulse response measurement techniques ［J］.Journal of the Audio Engineering Society，2002，50(4):249-262.

［5］孟子厚.厅堂声学测量中不同激励声源的比较［J］.应用声学，2005，24(1):19-23.Meng Zi-hou.Comparison of acoustic measurements with different sound sources in a concert hall ［J］.Applied Acoustics，2005，24(1):19-23.

［6］Torras Rosell A.Methods of measuring impulse responses in architectural acoustics ［D］.Copenhagen:Technical University of Denmark，2009.

［7］Ciric D，Pantic A，Radulovic D.Transient noise effects in measurement of room impulse response by swept sine technique［C］∥2011 10th International Conference on Telecommunication in Modern Satellite Cable and Broadcasting Services (TELSIKS).［S.l.］:IEEE，2011:269-272.

［8］饶丹.稳态噪声对最大长度序列测量的影响［J］.电声技术，2009，33(11):84-87.Rao Dan.Effect of steady noise on measurement with maximum length sequences［J］.Audio Engineering，2009，33(11):84-87.

［9］Schroeder M R，Atal B S.Computer simulation of sound transmission in rooms ［J］.Proceedings of the IEEE，1963，51(3):536-537.

［10］Farina A.Simultaneous measurement of impulse response and distortion with a swept-sine technique［J］.Proceedings of Audio Engineering Society Convention，2000，108:5093.

［11］Narendra K S，Gallman P.An iterative method for the identification of nonlinear systems using a Hammerstein model［J］.IEEE Transactions on Automatic Control，1966，11(3):546-550.

［12］杨春花.运用m 序列测量房间脉冲响应的技术研究［D］.天津:天津大学信息工程学院，2007.

［13］Kaizer A J M.Modeling of the nonlinear response of an electrodynamic loudspeaker by a volterra series expansion［J］.J Audio Eng Soc，1987，35(6):421-433.

［14］Morse P M C，Ingard K U.Theoretical acoustics［M］.United States:Princeton University Press，1986.

［15］Dietrich P.Uncertainties in acoustical transfer functions:modeling，measurement and derivation of parameters for airborne and structure-borne sound ［M］.Berlin:Logos Verlag Berlin，2013.

［16］Duda R O，Martens W L.Range dependence of the response of a spherical head model ［J］.J Acoust Soc America，1998，104(5):3048-3058.