考虑摩擦系数的沥青路面动态轴载换算*
韩丁 申飞 李凌林
(合肥工业大学 交通运输工程学院,安徽 合肥230009)
国内现有的道路设计方法通常将车辆荷载简化为双圆静态均布荷载,以双轮单轴BZZ-100(100 kN)为标准轴载,以设计弯沉值作为路面整体刚度的控制指标,对沥青混凝土面层、基层和底基层进行层底弯拉应力验算[1].实践证明现有规范设计方法具有较大的局限性,因而很多学者主张路面设计时应考虑移动荷载的影响.陈少幸等[2]提出了基于沥青层疲劳特性设计指标,推导出基于等效疲劳原则的轴载换算公式.胡朋等[3]使用动荷载系数功率谱密度、动荷载大小及分布概率,推导了考虑动荷载的当量轴载换算公式.各国学者也对动荷载作用下路面结构的动力响应进行了大量的理论研究.Lv 等[4]采用数学方法求解出Kevlin 地基上无限大板在移动荷载作用下动态响应的数值解.罗苏平等[5-6]依据Biot 理论和Fourier 变换等方法求解了路面各结构层在移动交通荷载作用下的动力响应.然而在计算路面动力响应理论解析解时,大多涉及到复杂的被积函数和多重广义积分运算,以致路面动力响应的求解受到了极大的限制.随着数值有限元仿真的发展,越来越多的动力学问题可以通过数值模拟来求解.张丽娟等[7]对重复荷载作用下的沥青混合料进行粘弹性有限元分析,预测出重复荷载作用下AC-13 基质和改性沥青混合料的变形.李凌林等[8]通过编写UTRACLOAD 和DSLOAD 子程序用有限元分析计算了水平移动荷载作用下的沥青路面响应,发现水平剪切力引起的竖向永久变形和由正压力引起的竖向永久变形相比同样严重.Patil 等[9]使用包含无限单元的三维有限元模型分析无限介质属性对有限元计算的影响,并获得采用无限边界时动荷载作用下路面结构的动力响应.目前数值模拟缺少有效性验证和多因素耦合作用下路面的动力响应分析.
针对以上问题,基于二维Lamb 问题验证了数值计算的有效性,并对三维数值计算中的阻尼参数和模型尺寸进行了比选.在考虑路面摩擦系数、荷载移动速度和轴载水平等因素的基础上,分析了刚性基层沥青路面的三维动力学数值计算模型,给出了以沥青层底弯拉应力为指标并考虑摩擦系数的动态轴载换算公式.
1 数值计算模型有效性分析
1.1 基于Lamb 问题的理论验证
Lamb 研究了垂直点源和线源脉冲分别位于弹性半空间体表面和内部时动力波的传播问题,Pekeris 等[10-11]对垂直点源Lamb 问题进一步分析获得了解析解.文中建立二维数值计算模型模拟垂直点源脉冲的传播,并与解析解进行比较验证数值计算的有效性.计算模型尺寸为10 m×10 m,单元类型为CPE4,材料泊松比为0.25,弹性模量为1.4 GPa,密度为2300 kg/m3,几何模型如图1(a)所示.脉冲荷载垂直向下施加于点A,荷载形式见图1(b).取B为观察点,图1(c)为B 点竖向位移计算结果和解析解的比较图,两类结果的曲线形状与幅值大小都比较接近,计算结果略大于解析解,该差异是由数值模型的计算效率和有限元计算时间步长设置导致.
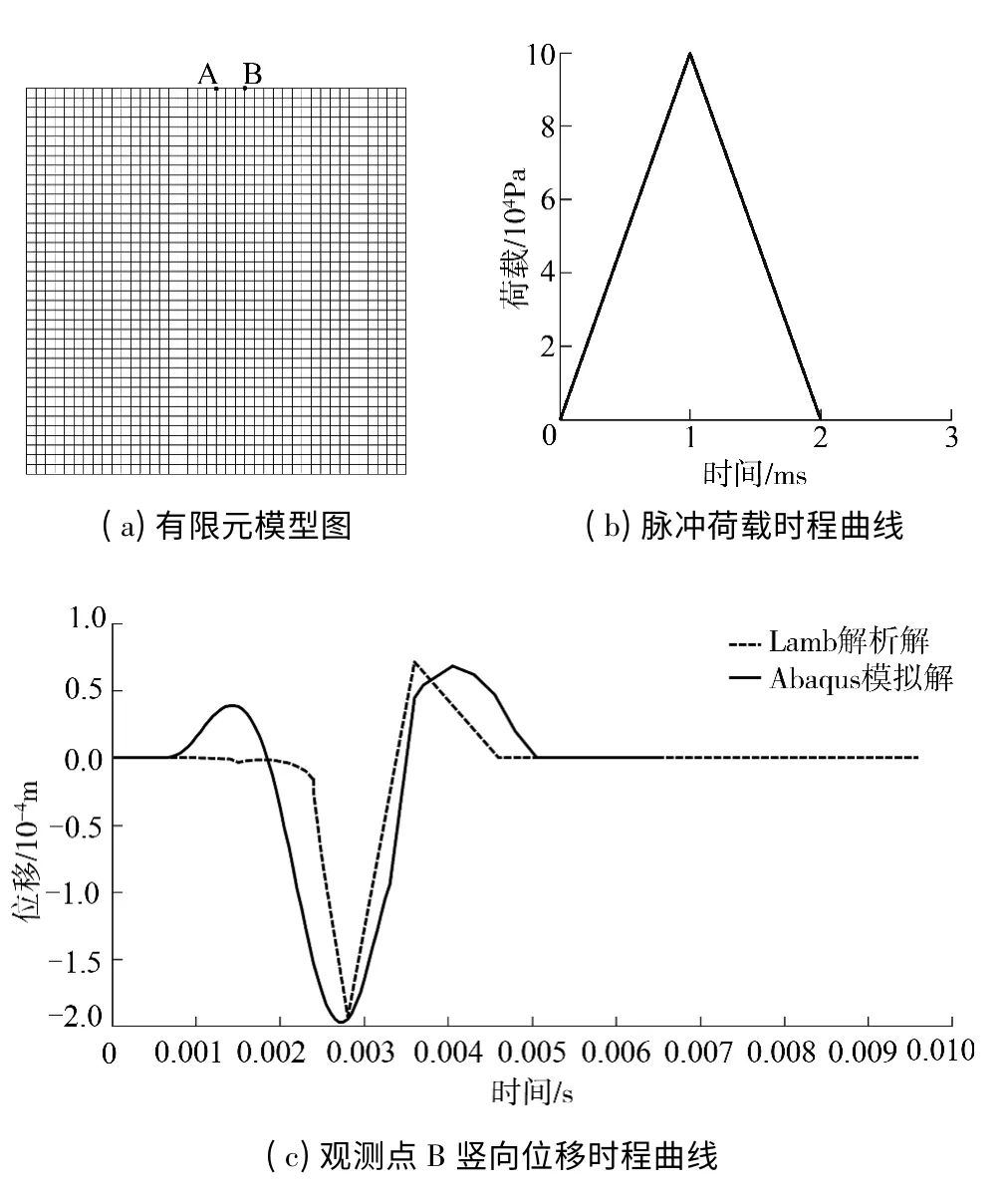
图1 数值计算有效性验证Fig.1 Verification of numerical calculation validity
1.2 阻尼参数的比选
为评价β 阻尼的影响,选取4 m×4 m×4 m 的立方体试件,动态弹性模量E = 2.0 GPa,密度ρ =2400 kg/m3,最小单元长度L=0.05 m,底面全约束,其他各面法向约束,荷载加载在半径为0.15 m 的1/4圆形承载板上,模型如图2所示.对承载板施加垂直向下的半正弦荷载,荷载幅值为0.1 MPa,作用时间为0.03 s.
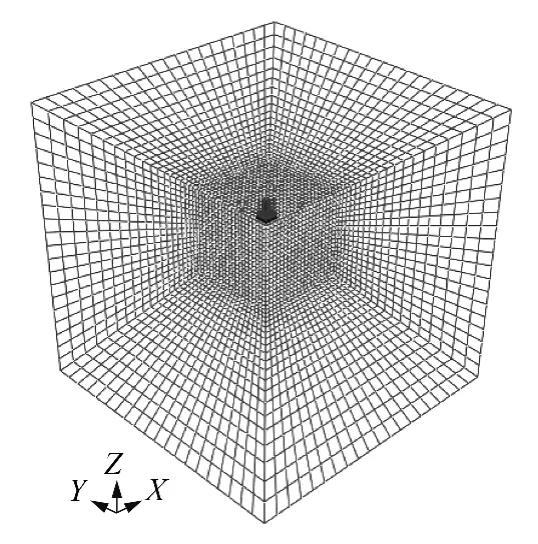
图2 阻尼因子分析模型Fig.2 Damping factor analysis model
无阻尼时的初始稳定时间增量计算式为

此时tsat=5.5×10-5s,β 阻尼因子优先使用小于或等于无阻尼计算的初始稳定时间增量.根据初始稳定时间增量选取的β 阻尼因子见表1.在计算模型中选取3 个表面点分别距加载点1.0、1.6 和2.2 m,作为测点1、2 和3,比较输出的位移时程曲线.未考虑阻尼情况下的位移曲线如图3(a)所示,振动曲线中包含较多振荡,根据输出曲线确定振动的幅值存在误差,通过消噪读取测点1、2 和3 的位移幅值分别为9.4×10-7、5.7×10-7和3.6×10-7m.
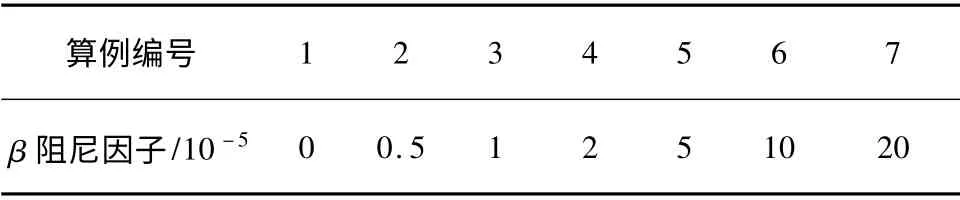
表1 β 阻尼因子数值Table1 β damping factor value
对比图3(a)和图3(b)发现,β 阻尼因子可以有效消除振荡,阻尼因子为5 ×10-6时各测点的位移幅值分别为9.46 ×10-7、5.9 ×10-7和3.77 ×10-7m,与未考虑阻尼的振动幅值对比,平均误差为2.95%.算例2 至6 位移曲线的对比如图3(b)、(c)和(d)所示,可见随着β 阻尼因子的增大,曲线逐渐趋于平滑,但振动幅值也有减小的趋势.计算发现β 阻尼因子取2 ×10-5和5 ×10-5时振动消噪的效果较好,且振动幅值与无阻尼情况相比变化不大,平均误差分别为0.84%和1.01%,因此β 阻尼因子取2 ×10-5.
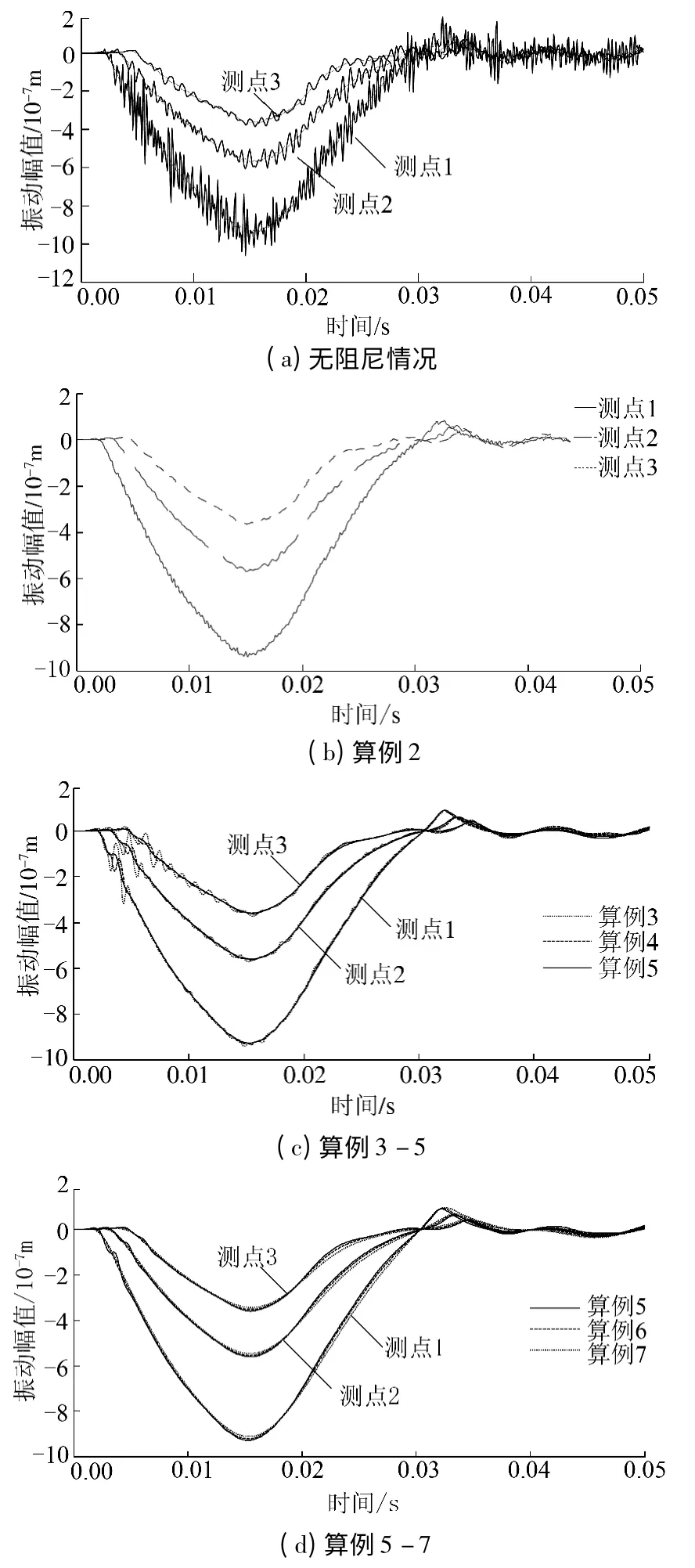
图3 不同阻尼情况下各测点振幅时程曲线Fig.3 Displacement-time history curves of measuring points in different damping conditions
1.3 数值计算模型尺寸
建立刚性基层路面结构有限元模型,模型尺寸为7 m×4.375 m×3.4 m,路面各结构层厚度及材料参数见表2.
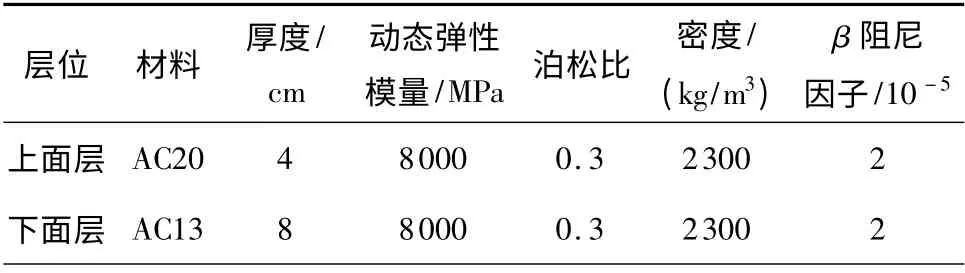
表2 沥青路面结构及材料参数表[12-13]Table2 Structure and material parameters of asphalt pavement[12-13]
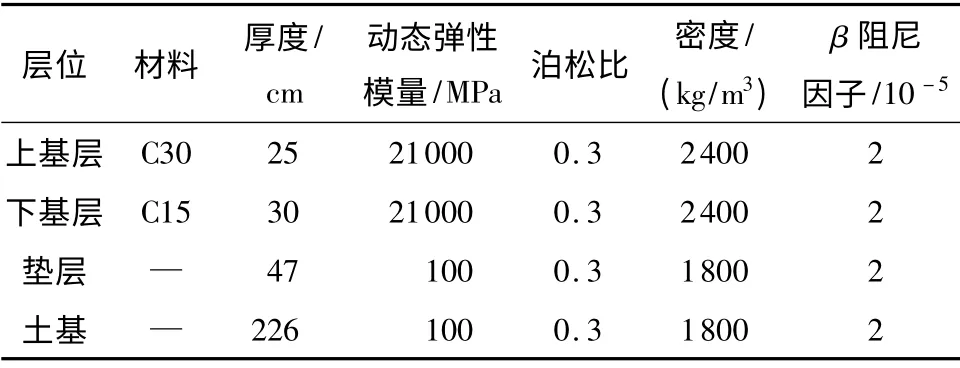
续表2
模型四周边界约束法向位移,底部边界全约束.在两个直径为0.213 m 的圆形加载面上施加荷载,通过加载面的移动实现荷载的移动.对荷载通过区域的路面结构网格进行加密,如图4所示.
图4 移动荷载作用下沥青路面模型Fig.4 Model of asphalt pavement under moving load
1.4 模型尺寸验证
为确定有限元模型尺寸的合理性,建立无限元模型进行对比计算,车辆荷载采用标准轴载BZZ-100,速度为80 km/h,沿z 轴正方向运动,路面摩擦系数为0.5[14].选取的应力输出位置为加载面行驶轨迹中间段的圆心正下方,分析路面结构的层底动态弯拉应力和沥青面层的动态剪应力.
如图5、6 所示,有限元和无限元模型的弯拉应力曲线基本一致,有限元模型剪应力计算值大于无限元模型计算值,两类模型误差较小.剪应力存在差异的原因是有限元模型底部全约束,而无限元模型能实现无限远边界条件.考虑到计算效率和推广性,文中采用有限元模型.
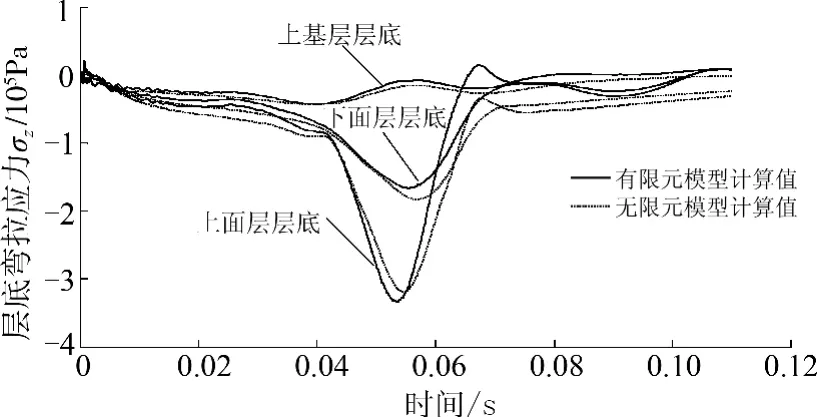
图5 层底弯拉应力σz时程曲线Fig.5 Time curves of bottom flexural stres σz
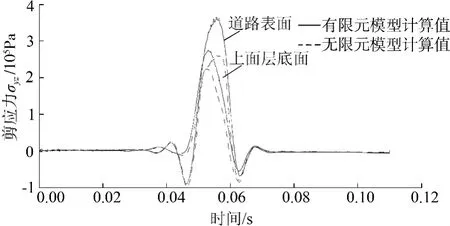
图6 剪应力σyz时程曲线Fig.6 Time curves of shear stress σyz
2 结构动力响应影响因素分析
移动荷载作用下路面结构的动力响应非常复杂,除与路面材料特性和路面结构组合有关外,还受车速、路面摩擦系数和车辆轴载等其他因素的影响.
车辆荷载采用标准轴载BZZ-100,速度为80 km/h,沿z 轴正方向运动,路面摩擦系数为0.5[14],层底弯拉应力观察点位置为动载行驶轨迹中间段加载面圆心的正下方.计算发现各结构层中平行于行驶方向(沿z 轴)的弯拉应力σz均大于垂直于行驶方向(沿x 轴)的σx,所以选取σz进行分析.路面各结构层层底弯拉应力时程曲线如图7所示,可以看出层底弯拉应力σz在路面结构中衰减很快,如上面层层底为0.332 MPa,下面层层底为0.167 MPa,上基层层底为0.044 MPa.因此,汽车匀速行驶状态下荷载的弯拉作用主要集中于沥青面层,对刚性基层及以下区域的影响明显变小.
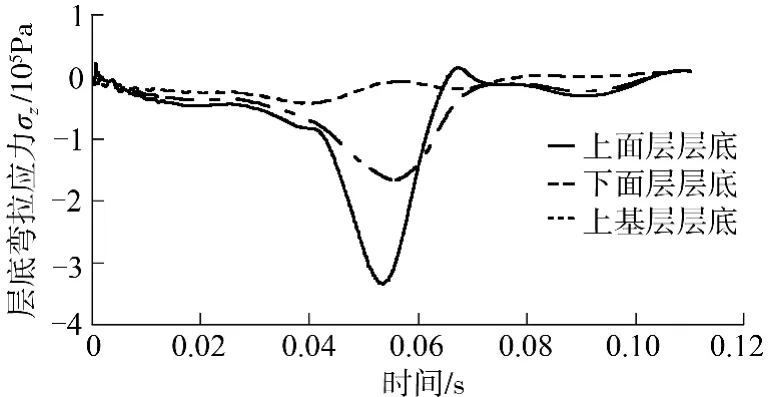
图7 层底弯拉应力时程曲线Fig.7 Bottom flexural stress-time curves
2.1 路面摩擦系数
根据文献[14]中选取接触面摩擦系数为0.3、0.5、0.7 和0.9,其他工况保持不变,路面各结构层层底弯拉应力时程曲线如图8所示.路面摩擦系数由0.3 变为0.9 时,上面层层底弯拉应力由0.290 MPa 增加到0.450 MPa,表明改变摩擦系数有明显影响.
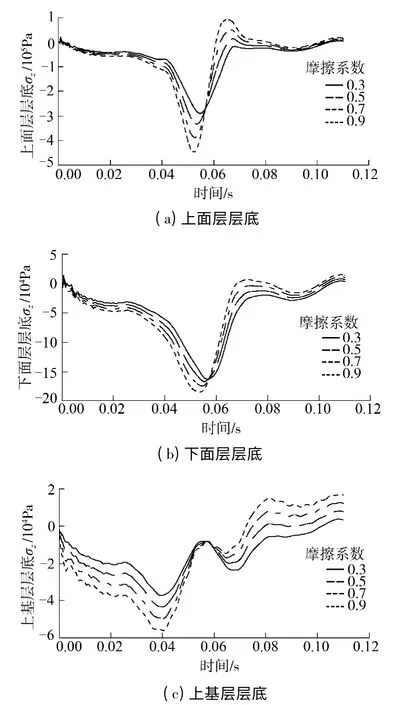
图8 不同摩擦系数下层底弯拉应力时程曲线Fig.8 Time history curves of bottom flexural stress at different friction coefficients
2.2 荷载移动速度
荷载移动速度分别取60、80、100 和120 km/h,其他工况保持不变,路面各结构层层底弯拉应力时程曲线如图9所示.可以发现荷载移动速度发生变化后,路面各结构层所受弯拉应力仍保持稳定,说明在路面平整度较好且车辆保持匀速行驶的情况下,荷载移动速度的影响很小,即通过车速控制措施难以减轻对路面结构的损坏.
2.3 车辆轴载
轴载分别取6、10、16 和20 t,其他工况保持不变,路面各结构层层底弯拉应力时程曲线如图10所示.当轴载由6t 增加到20t 时,上面层层底弯拉应力值由0.200MPa 增加到0.667MPa,增加了233.5%,下面层层底弯拉应力值由0.100MPa 增加到0.334MPa,增加了234.0%,上基层层底弯拉应力值由0.026 MPa 增加到0.087 MPa,增加了234.6%.
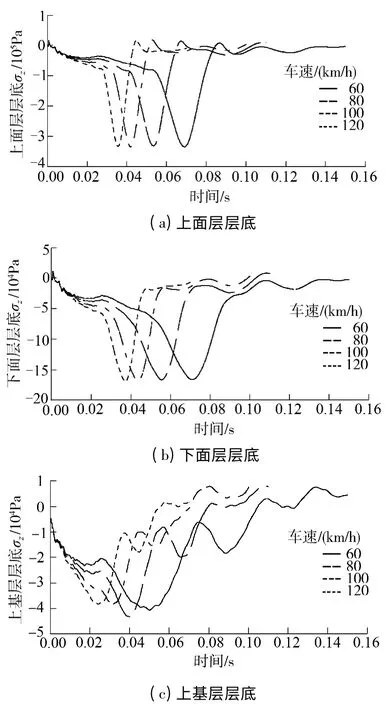
图9 不同荷载速度作用下层底弯拉应力时程曲线Fig.9 Time history curves of bottom flexural stress at different speeds
通过层底弯拉应力的分析,可以发现应力值增幅与荷载增幅非常接近,路面各结构层所受应力随轴重呈线性变化.
3 当量轴载换算
3.1 轴载换算理论公式
美国公路工程师协会(AASHTO)根据路面使用性能变化基本方程式推导的轴载换算公式为目前大多数设计的基础,其柔性路面当量轴载换算公式为[15]
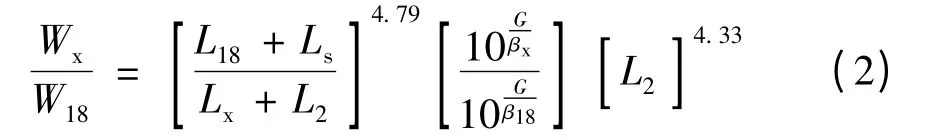
式中,W18为标准轴载(80 kN)作用次数,Wx为被换算轴载作用次数,L18为标准轴载,Lx为被换算轴载.βx=为最终服务性指数,Ls为标准轴载,L2为被换算轴载,下标数字1 表示单轴,2 表示双轴,3 表示三轴,SN 为路面结构数.
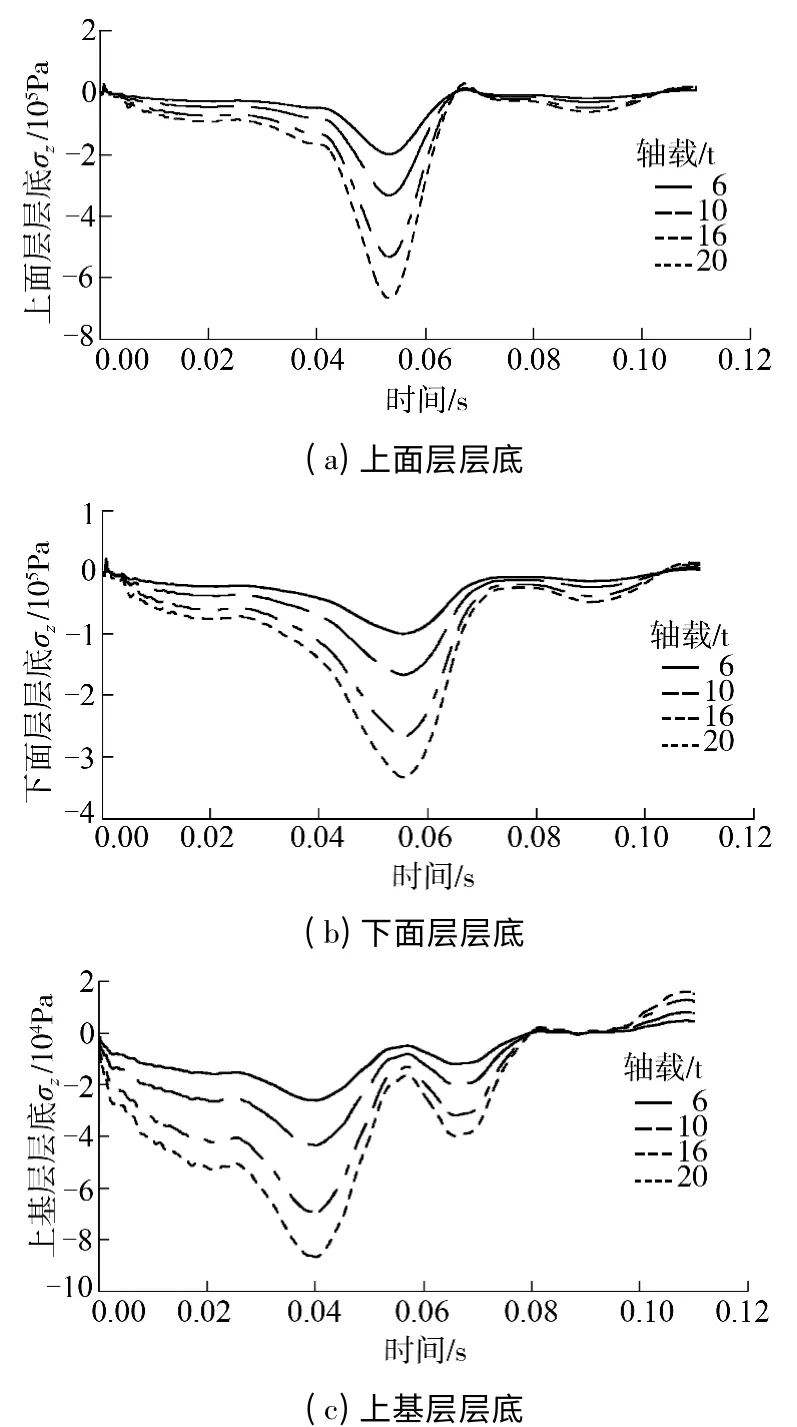
图10 不同轴载作用下的层底弯拉应力时程曲线Fig.10 Time history curves of bottom flexural stress at different axle loads
我国现行规范[1]根据弹性层状体系理论,对于单轴双轮组在不同轴载作用下的层底弯拉应力比的简化公式描述为

式中,Pi为第i 个轴载大小,σi为Pi产生的层底弯拉应力,a、b 为系数.
设计层底弯拉应力σd为

式中,N 为轴载作用次数,A、c 为系数,根据轴载换算等效原则计算获得轴载换算简化公式:
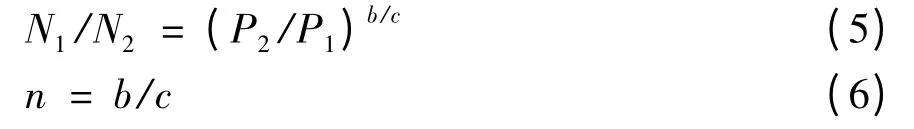
式中,Ni为第i 个轴载的作用次数.目前沥青层底弯拉应力轴载换算公式中换算指数n 为4.35,它仅适用于单后轴介于50 ~130 kN 之间的情况.随着轴载的增加,现行的静态换算公式逐渐无法满足安全需求.
3.2 考虑摩擦系数的动态轴载换算
由图9可以发现,荷载移动速度对路面结构层层底弯拉应力的影响较小,因此在进行轴载换算因素分析时不考虑速度的影响,结合实际,取荷载移动速度80km/h.不同摩擦系数和轴载作用下沥青层层底弯拉应力峰值见图11,可以看出,轴载和摩擦系数的改变对沥青层底弯拉应力的影响非常明显.
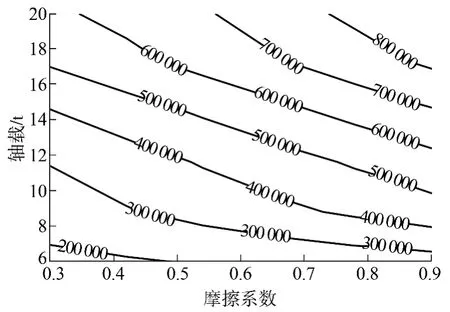
图11 不同摩擦系数及轴重作用下沥青层底弯拉应力峰值(单位:Pa)Fig.11 Bottom flexural stress peaks of asphalt layer under different friction coefficients and axle loads(Unit:Pa)
根据不同轴重和路面摩擦系数下的沥青层底弯拉应力计算结果,按式(7)计算以沥青层底弯拉应力为换算指标的轴载换算系数a 和b.计算时取p =100 kN,σ 为对应的沥青层底弯拉应力,

图12为参数a、b 数值示意图,可以发现随摩擦系数的变化,参数a、b 变化范围较小,平均值分别为1.00 和1.01.其中b 值大于《公路沥青路面设计规范》(JTG D50—2006)的轴载换算系数0.87.
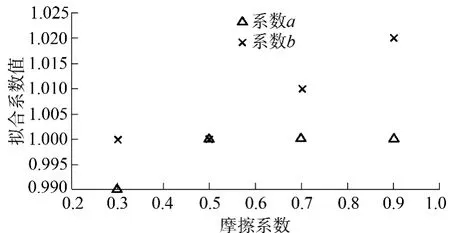
图12 参数a、b 数值Fig.12 Values of parameters a and b
文献[1]中认为沥青层底允许弯拉应力按式(4)表达,其中c=0.2 最符合沥青路面的疲劳特性.依据式(5)和式(6),考虑路面摩擦系数的动态轴载换算公式为

式中,n 为5.05,大于当前规范值4.35.因此,使用考虑摩擦系数的动态轴载换算公式计算的累积作用轴次明显大于当前规范静载公式的换算结果.
4 结论
依据垂直点源的二维Lamb 问题解析解验证了数值计算的有效性,并分析选择合理的阻尼参数和模型尺寸进行三维数值计算,得出以下结论:
(1)摩擦系数由0.3 变为0.9 时,上面层层底弯拉应力增加了55.1%;路面平整度保持较好,荷载匀速移动时,改变移动速度,路面各结构层所受应力保持稳定.轴重由6 t 增为20 t 时,路面各结构层层底弯拉应力增加了234%左右.路面各结构层所受应力随轴重呈线性变化,摩擦系数对道路各结构层层底弯拉应力明显,车辆匀速行驶时车速对路面动力特性影响较小.
(2)考虑动荷载作用时的当量轴载换算指数n为5.05,大于当前规范值4.35.因此使用动态轴载换算公式计算的累积作用轴次明显大于当前规范静载公式的换算结果,使用考虑摩擦系数的动态轴载换算公式进行路面结构设计更加安全.
[1]JTG D50-2006,公路沥青路面设计规范[S].
[2]陈少幸,虞将苗,任伟新,等.基于疲劳等效的柔性基层沥青路面轴载换算研究[J].武汉理工大学学报:交通科学与工程版,2010,34(4):762-768.Chen Shao-xing,Yu Jiang-miao,Ren Wei-xin,et al.Study on axle load conversion of flexible basement asphalt based on fatifue equivalen[J].Journal of Wuhan Uniwersity of Technology:Transportation Science & Enginee-ring,2010,34(4):762-768.
[3]胡朋,潘晓东.考虑动荷载影响的当量轴载换算理论分析[J].哈尔滨工业大学学报,2011,43(6):91-95.Hu Peng,Pan Xiao-dong.Equivalent standard axle load conversion in theory considering dynamic load[J].Journal of Harbin Institute of Technology,2011,43(6):91-95.
[4]Lv Peng-min,Tian Run-li,Liu Xiao-yun.Dynamic response solution in transient state of viscoelastic road under moving load and its application[J].Journal of Engineering Mechanics,2010,136(2):168-173.
[5]罗苏平,但汉成,李亮,等.移动交通荷载下饱和沥青路面的水力耦合分析[J].华南理工大学学报:自然科学版,2012,40(2):104-111.Luo Su-ping,Dan Han-cheng,Li Liang,et al.Coupled hydro-mechanical analysis of saturated asphalt pavement under moving traffic loads [J].Journal of South China University of Technology:Natural Science Edition,2012,40(2):104-111.
[6]Fang Xue-qian,Yang Shao-pu.Dynamic response of road pavement resting on a layered poroelastic half-space to a moving traffic load[J].International Journal for Numerical and Analytical Methods in Geomechanics,2014,38(2):189-201.
[7]张丽娟,陈页开.重复荷载下沥青混合料变形的粘弹性有限元分析[J].华南理工大学学报:自然科学版,2009,39(11):12-16.Zhang Li-juan,Chen Ye-kai.Viscoelastic finite element analysis of deformation of asphalt mixtures under repeated load[J].Journal of South China University of Technology:Natural Science Edition,2009,39(11):12-16.
[8]李凌林,黄晓明.水平移动荷载作用下沥青路面的永久变形[J].华南理工大学学报:自然科学版,2011,39(3):125-129.LiLing-lin,Huang Xiao-ming.Permanent deformation of asphalt pavement under horizontal moving load[J].Journal of South China University of Technology:Natural Science Edition,2011,39(3):125-129.
[9]Patil V A,SawanV A t,Deb Kousik.3D finite-element dynamic analysis of rigid pavement using infinite elements[J].International Journal of Geomechanics,2013,10(3):533-544.
[10]Pekeris C L.The seismic surface pulse[J].Proceedings of the National Academy of Sciences of the United States of America,1955,41(7):469-480.
[11]刘凯欣,刘广裕.垂直点源问题的一个精确解[J].科学通报,2004,49(5):419-423.Liu Kai-xin,Liu Guang-yu.An exact solution for a normal point source problem[J].Chinese Scinece Bulletin(In Chinese),2004,49(5):419-423.
[12]侯芸,孙四平,郭忠印.移动荷载下刚性路面响应的参数影响分析[J].同济大学学报:自然科学版,2003,30(1):31-35.Hou Yun,Sun Si-ping,Guo Zhong-yin.Dynamic response sensitivity analysis of plate on elastic foundation subjected to moving point loads [J].Journal of Tongji University:Natural Science Edition,2003,30(1):31-35.
[13]黄兵,吴玉,艾长发,等.结构参数对沥青路面动态响应的影响[J].公路交通科技,2013,30(9):8-13.Huang Bing,Wu Yu,Ai Chang-fa,et al.Influence of structural parameters on dynamic response of asphalt pavement[J].Journal of Highway and Transportation Research and Development,2013,30(9):8-13.
[14]胡朋,潘晓东.不同状态下路面摩擦系数现场试验研究[J].公路,2011,2(2):20-24.Hu Peng,Pan Xiao-dong.Field experiment and study on pavement friction coefficient under different conditions[J].Highway,2011,2(2):20-24.
[15]王端宜,张肖宁.路面结构设计理论[M].广州:华南理工大学交通学院,2005:63-65.

