基于修正算法的高速公路路段旅行时间估计*

沈旅欧 庄岩浩 刘伟铭† 巫威眺

(1.华南理工大学 土木交通学院，广东 广州510640;2.西南交通大学 交通运输与物流学院，四川 成都610031)

路段旅行时间估计用于定位车辆在道路上的位置，进而准确估算路段流量，同时其也是进行旅行时间可靠性研究必需的数据基础［1］.文献中路段旅行时间估计主要有两种方法:轨迹法和交通流理论法.文献［2-6］介绍了几种采用交通感应器数据的轨迹法.其中，Van Lint 等［5］提出了基于分段线性速度(PLSB)的轨迹法，路段速度是通过对上游和下游传感器的速度进行线性插值得到.Shen 等［6］利用感应器数据对比分析了不同的插值方法对路段旅行时间估计的影响.另外，Nam 等［7-12］对基于交通流理论的旅行时间估计方法进行了研究，这种方法应用随机排队理论和路段上的车辆数进行时间预测，具有可捕获动态交通流特征的优点.近年，于德新等［13］则提出了一种基于GPS 数据及车辆运行特性分析的单车路段行程时间估计方法.

目前，国内外对旅行时间估计的研究几乎都是基于感应器、浮动车或GPS 数据，但在我国高速公路上感应器的安装率不高且数据欠稳定.在我国，高速公路基本都采用封闭式收费系统，此系统详细记录了车辆进出高速的相关信息.然而，仅有少数学者利用收费系统数据开展研究.其中较早的有杨晓光［14］对数据进行预处理后直接采用系统记录计算旅行时间，却发现误差较大.后来，王海燕等［15］针对国内目前检测器安装量不足，提出了一种基于收费系统数据的高速公路出入口OD 流量推算方法.最近，沈强［16］探讨了利用高速公路收费数据作为数据资源进行路网运行状态评价的可行性.

旅行时间可靠性研究必须要有长时间的数据记录作为支撑，如果能充分利用高速公路历史收费系统数据，开展旅行时间可靠性研究，具有现实意义.路段流量与旅行时间可靠性密切相关，因此，通过一套准确的旅行时间估计方法准确估算路段流量对旅行时间可靠性研究至关重要.然而，收费系统的记录与实际的路段旅行时间存在偏差［14］，这很大程度影响了直接应用收费系统数据，导致偏差是由于3 个不确定因素:①数据噪声，如特殊驾驶习惯、交通事故、突发事件等;②车辆在收费站产生的延误;③短距离行驶的车辆由于刚进入高速很快就要驶离高速，驾驶员通常都选择右侧车道，造成收费系统记录的短距离行程时间与此路段的实际平均旅行时间不符.有鉴于此，文中研究利用高速公路数据对路段旅行时间进行修正，以期获取准确的路段旅行时间估计，进而准确估算路段流量，为进一步进行旅行时间可靠性研究提供必要支持.文中首先针对数据噪声提出了数据预处理的方法，然后针对收费系统记录的较短距离旅行时间跟实际路段旅行时间误差较大的问题提出了修正算法，依据修正算法得到了更准确的路段旅行时间数据，在此基础上通过轨迹法计算所得的所有路段旅行时间矩阵，最后采用某收费系统数据验证了此算法在旅行时间估计中应用的有效性.

1 路段旅行时间估计

在展开论述之前，为进行后面的分析，提出如下4 个定义:①一个上游入口和一个下游出口组成一个“出入口对”;②一个“出入口对”中的入口或出口可抽象为一个“节点”;③两个“节点”之间为一个“路段”;④两个相邻“节点”之间为一个“基本路段”.

高速公路的路段旅行时间是车辆在一个路段两个节点之间的平均旅行时间.

高速系统记录了车辆从入口到出口的完整旅行时间，因此不仅包含路段旅行时间，还包含其他延误时间.路段旅行时间估计的目的是通过一定的方法估计车辆的路段旅行时间.

1.1 平均旅行时间定义

平均旅行时间t(p)i，j的定义为

1.2 数据预处理

系统记录旅行时间不仅包含路段旅行时间，还包含其他延误时间(如收费站延误).除此之外，受一些不确定因素(如:中途停车、个别特别快或特别慢的行驶速度等)影响，收费系统的记录中从同一时间区间出发的车辆中存在少量车辆的旅行时间与其他车辆的存在很大差异，这少量的异常旅行时间数据称为噪音.因此，需要对数据进行预处理，利用概率统计方法去除噪音.

根据文献［17］，相同时间区间出发的车辆旅行时间服从正态分布.基于此，定义如下旅行时间的统计量.

设从时间区间p 出发，行驶在出入口对i、j 之间车辆的平均旅行时间为

式中，N 表示时间区间p 内出发的车辆数，i 为入口节点，j 为出口节点.

旅行时间标准差S 为

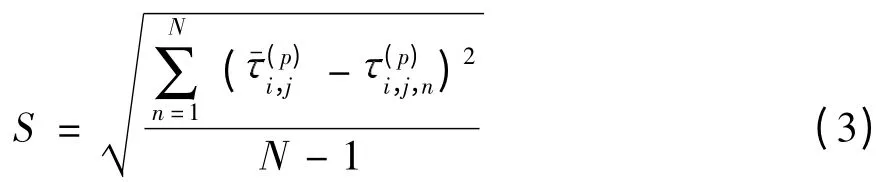
(1)提取旅行时间阈值下限.高速公路一般限速120 km/h，假设最大速度为限速的115%，则最小旅行时间=路程/最大速度.以此最小旅行时间为数据的下限，当数据中的旅行时间小于此阈值时被判断为无效数据，将其从样本中剔除;

(2)重新计算样本中剩余数据的均值-(p)i，j 和方差S;

1.3 基于轨迹法的路段旅行时间估计

在利用收费系统数据进行路段旅行时间估计时，由于较长路段往往包含若干基本路段的旅行时间数据，但是这样估计的旅行时间往往是按照从出发地点开始的每个时间区间，比如10 min 时段内所有出发的车辆到达下游出口的平均旅行时间，而车辆在向下游行驶的过程中，时间也在向前推移.因此，要准确地估计出上游各入口在各时段内到达下游出口的旅行时间需要考虑车辆随时间推移的行驶轨迹特性.因而可运用轨迹法对路段旅行时间进行估计.

轨迹法［5-6］的主体思路是通过重构车辆在路段上的虚拟行驶轨迹及时间轨迹，估计车辆的路段旅行时间.假设一条道路有K 个出入口，即有K 个节点，K-1个基本路段，如图1所示.

图1 路段定义示意图Fig.1 Definition of road sections

假设沿线各基本路段之间的旅行时间是独立的，同时还假设在同一路段sk，k+1的同一个较小的时间区间p 内的同一类型车辆行驶速度恒定.这样，路段和时间可以抽象为一个由时空网格单元{sk，k+1，p}(k ∈［1，2，…，K -1］，p ∈［1，2，…，P］)组成的时空网格区域，sk，k+1表示一个基本路段，p 表示时间区间，如图2所示.在每一个时空网格单元{sk，k+1，p}内，速度v(sk，k+1，p)是恒定的.因此从任意一个节点k 出发的车辆，可以找到其进入和离开每一个时空网格单元{sk，k+1，p}的位置和时刻，把车辆经过的所有时空网格单元的进入点和离开点连接起来，就是车辆的行驶轨迹.

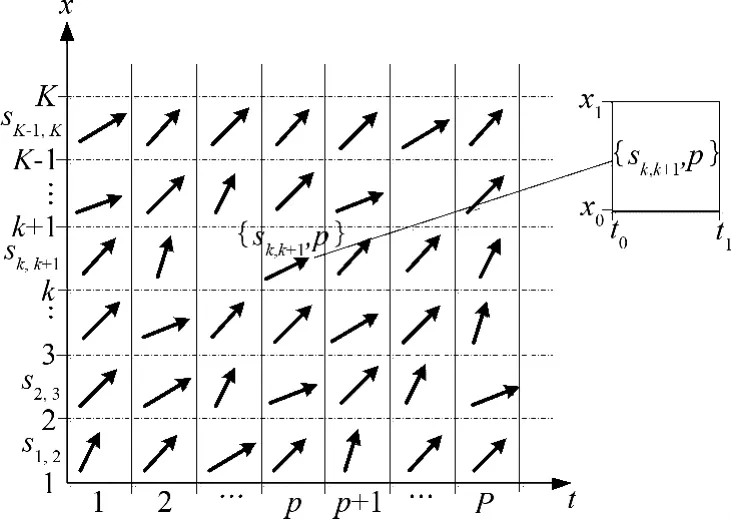
图2 时空网格Fig.2 Time-space grid

将每个时空网格单元{sk，k+1，p}看成一个矩形区域，它的边界为时间轴上的［t0，t1］，空间轴上的［x0，x1］.{x0，t0}表示车辆进入当前矩形区域的位置和时刻，{x*，t*}表示车辆离开当前矩形区域的位置和时刻，{x*，t*}同时也是车辆进入下一矩形区域的初始位置和时刻.因此，某个路段sk，k+1的距离范围为［x0，x1］，车辆贯穿整个路段至少需要通过一个时空网格单元.

车辆离开矩形区域{sk，k+1，p}的位置x*和时间t*可以通过如下方法计算:

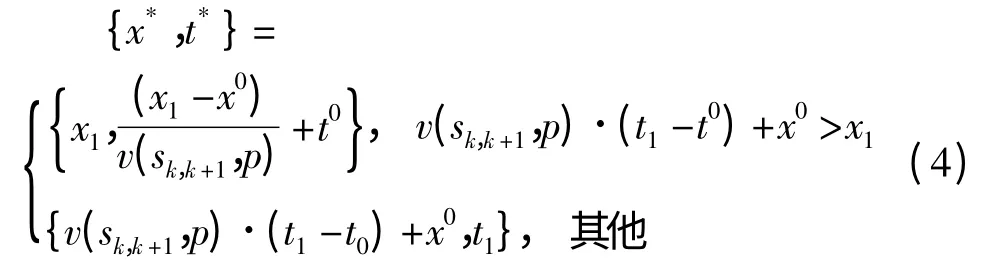
由时间区间p 出发的车辆在路段sk的行驶轨迹x(t)可以通过如下方法计算:

5）机械类课程三维建模与仿真平台可通过网络实现区域共享甚至可以全国共享，不同地域的学校中的学生可以进行相同的虚拟实验，彼此交流。

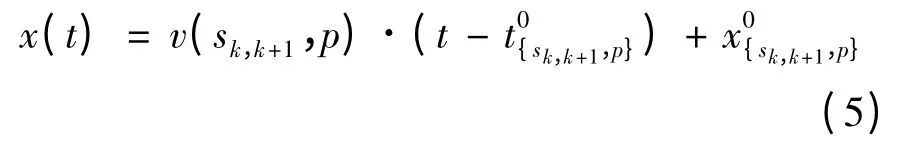
如图3所示，车辆由时空网格单元{sk，k+1，p}进入的位置和时刻，以及从另一个时空网格单元{sk，k+1，p+1}离开时的位置和时刻，可通过式(4)、(5)计算得到.因此，车辆在整个路段sk，k+1的旅行时间Travel，当整段旅程含多个路段时，只需要通过计算车辆在各个路段上的旅行时间，然后将它们求和，就可以估计出车辆在整段旅程的完整旅行时间.因为同一时间区间内由同一节点进入道路的车辆在宏观上具有相似的轨迹，因此只需获得这些车辆在每一个时空网格中的平均行驶速度，就可以计算这些车辆的平均行驶轨迹.

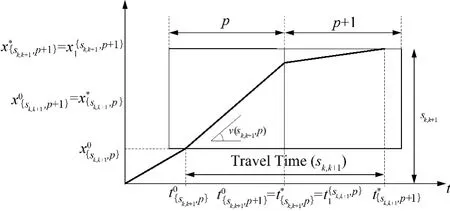
图3 时空网格中车辆的虚拟行驶轨迹Fig.3 Virtual trajectory of vehicle in Time-Space grid

2 路段速度计算

高速公路收费系统数据记录了路径上K 个节点之间的旅行时间，同一个时间区间p(p = 1，2，…，P)出发的车辆，任意两个节点之间的旅行时间经过1.2 节的数据预处理后，可以排列成一个(K - 1)× (K - 1)上三角时间矩阵T(p):

式中，k(k = 1，2，…，K -1)表示当前出发节点.此上三角矩阵记录了车辆平均旅行时间.

应用轨迹法时，需知道相邻两个节点之间基本路段的速度.由于路径上任意两个节点间的距离sk，k+1是已知的，因此仅需要知道基本的路段旅行时间，就可以计算车辆在基本路段的速度.

根据矩阵，定义“原始速度”为

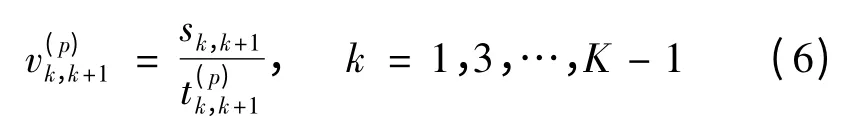
2.1 时间区间搜索

由于收费系统记录了完整的旅行时间数据，因此可以计算从任意一个节点的某个时间区间出发的车辆到达下游节点所花费的平均旅行时间，以及到达时间区间.也可以通过车辆到达某个节点所在的时间区间，反推车辆从上游节点出发的时间区间和路段旅行时间.

前面介绍了T(p)为一个(K - 1)× (K - 1)的上三角时间矩阵，其中p(p = 1，2，…，P)为车辆的出发时间区间，T(p)包含该时段从一条路径上各个节点出发的车辆在路径上任意两个节点之间的平均旅行时间.统计一天中P 个时间段的数据，就可得到P 个上三角矩阵，即(T(1)，T(2)，T(3)，…，T(P)).

通过搜索表1，可以根据出发节点和出发时间区间查找到达目的节点所处的时间区间，也可以通过目的节点和到达目的区间的时间区间反推出出发节点的出发时间区间.相应的搜索算法流程图如图4所示.其中，图4(a)为已知当前出发时间区间r 和出发节点i，目的节点为j，搜索车辆到达目的节点j时所处的时间区间p 和时间矩阵T(p)的搜索算法流程图.图4(b)为已知车辆在路径上的出发节点i，目的节点为j，以及车辆到达节点j 的时间区间p，查找车辆出发时间区间r 和时间矩阵T(r)的搜索算法流程图.

表1 旅行时间二维表Table1 Two-dimension table of travel time

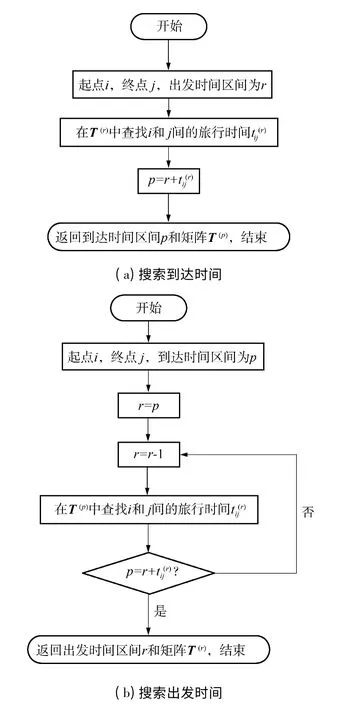
图4 时间搜索算法流程图Fig.4 Flow diagram of time searching algorithm

2.2 路段旅行时间获取

高速公路收费系统数据直接记录了车辆在收费出入、口的时间，因此，两者相减可直接得到两出、入口之间的旅行时间.同时，由于出入口对之间存在内嵌现象，即有些距离较长的出入口对包含了一些相对较短的出入口对.在这种情况下，由较长的出入口对所包含的较短的出入口对的旅行时间还可以通过出入口对之间的旅行时间相减的方式来获取，即两段内嵌路段之间的旅行时间之“差”.

例如，一条路径上有3 个节点A、B、C，分别对应3 个时间区间r、p、q，表示一辆车由时间区间r 内从A 出发，经过B、C 时所处的时间区间分别为p、q，其中p、q 可以通过2.1 节所述方法计算.在延误时间较短的情况下，AB 间的路段旅行时间近似于从A 到B 的车辆系统记录旅行时间，即;同时，也可以通过车辆在AC 和BC 两个路段的平均旅行时间之“差”得到，即tAC-tBC.但是tAC和tBC并不属于同一时间区间.因为tAC表示的是某个时段内由A 出发，行至终点为C 的车辆的旅行时间，假设一辆车由时间区间r 从A 出发，在时间区间p 到达B，并继续向C 行驶，此时tAC应属于T(r)，表示为，相应地tBC为时间区间p 从B 出发，行至终点为C 的车辆的旅行时间，因此tBC属于T(p)，应表示为.

在现实条件下，延误是不可忽略的，因此以上所述的路段旅行时间与实际路段旅行时间还存在一定的误差，但由于其包含了行驶过程中距离和时间要素，因此其对下文的研究至关重要.

2.3 路段旅行时间修正算法

当车辆行驶路程越长，其消耗在出、入口收费站的延误时间占全程所记录的旅行时间的比例越小，而车辆在路段上的实际行驶时间所占的比例越大，所以收费系统记录的旅行时间随着车辆行驶路程的增加而越接近车辆在道路上的实际旅行时间.可以得出，第2 节中的上三角旅行时间矩阵T(p)中越靠近右上角的数据越准确，而越靠近对角线即路段越短的数据越不准确.而依据轨迹法，所有路段的旅行时间都可以由对角线上的元素推得.因此，在通过2.1 节获取到达和出发时间的基础上，需要一个修正算法，基于已知的旅行时间矩阵T(p)，推导出能准确反映各个基本路段的旅行时间数据，即对角线上各元素.

在2.2 节中已知获取任意基本路段sk，k+1旅行时间的方法，可以用两个关联路段的旅行时间之“差”来表示.而采用不同计算方法的旅行时间之间存在的差异是由于车辆行驶的距离长短差异造成的.由于“系统记录旅行时间”与“路段旅行时间”存在偏差，需要通过一定修正算法得到“路段旅行时间”.自然地可以把用来表示基本路段sk，k+1的所有“旅行时间”，赋予一个与旅行时间数据所对应的路段长度一致的权值，即:路段距离越长权值越大，并把所有“旅行时间”乘以此权重后相加得到最终的“修正路段旅行时间”.

从节点k 到节点k +1 的旅行时间修正算法如下.

1)当k=1 时，

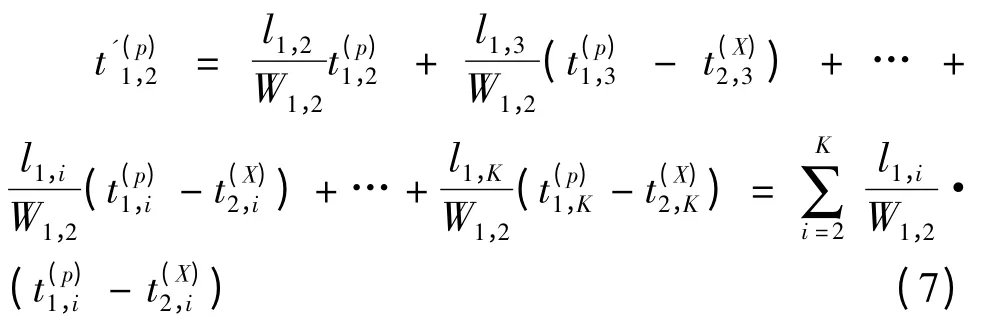
其中

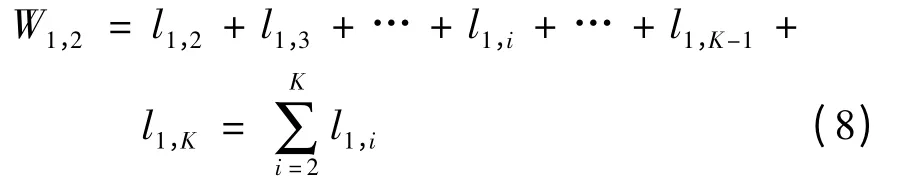
式(7)中p 为车辆从节点1 出发时所处的时间区间，X 为车辆从节点1 行驶到节点2 时所处的时间区间，W1，2为车辆行驶路程之和.

2)当1 ＜k ＜K -1 时，

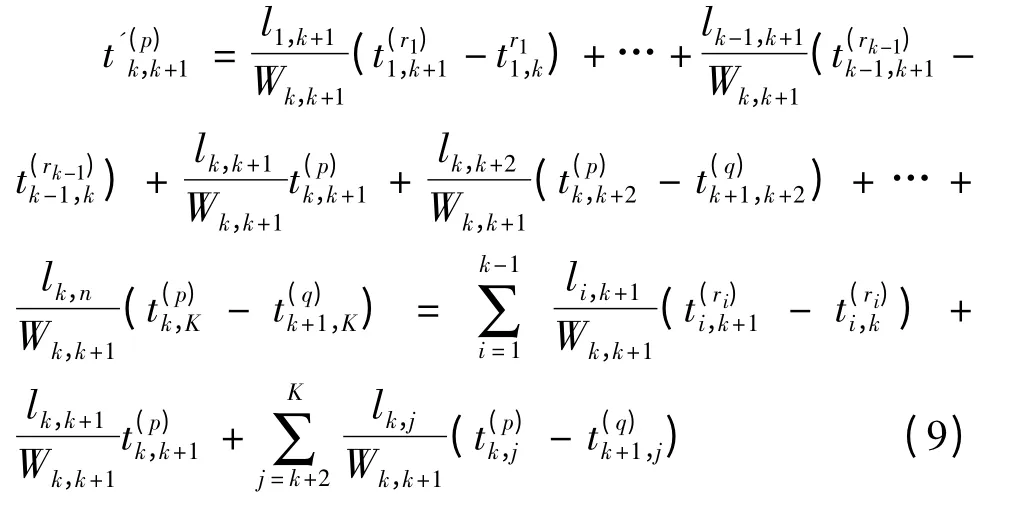
其中，

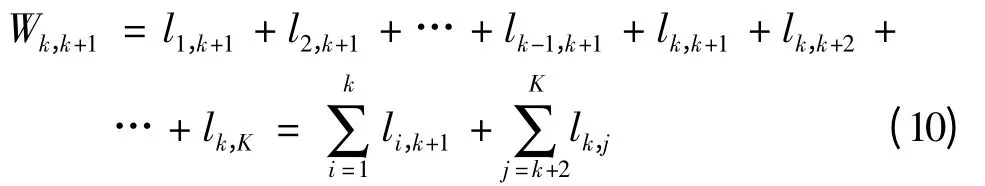
式(9)中p 为车辆从当前节点k 出发的时间区间，ri(i=1，2，…，k -1)为从k 节点上游的k -1 个节点出发的车辆的出发时间区间，在时间区间ri从上游k -1 节点出发的车辆行驶到节点k 时所处的时间区间，恰为p，而q 为由时间区间p 从节点k 出发的车辆到达下游节点k +1 时所处的时间区间，Wk，k+1为车辆行驶路程之和.

3)当k = K -1 时，

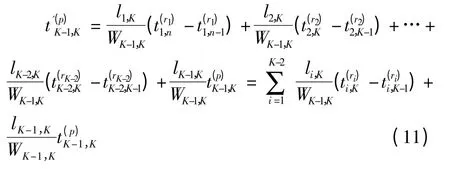
其中，

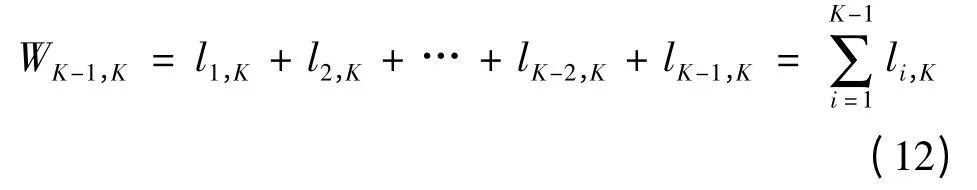
式(11)中，p 为车辆从当前节点K-1 出发的时间区间，ri(i=1，2，…，K-2)为从K -1 节点的上游K-2 个节点出发的车辆的出发时间区间，由时间区间ri上游K-2 个节点出发的车辆行驶到节点K -1时所处的时间区间恰为p，WK-1，K为车辆行驶路程之和.

最后，相邻节点k 到k+1(k=1，2，3，…，K -1)的旅行时间经过修正算法修正为.

鉴于轨迹法采用路段速度直接计算旅行时间，根据上面修正的旅行时间，可以计算修正路段速度:

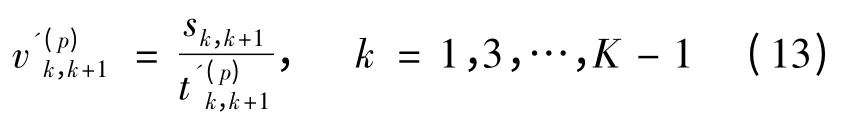
当划分的时间区间足够小，每个时间区间内计算出的修正路段速度可以直接作为该时间区间内车辆在路段上的行驶速度，运用轨迹法进行路段旅行时间估计.

3 算例

基于某高速公路2011年的收费系统数据对文中提出的算法进行验证.某高速公路全长122.8 km，宽33.1 m，双向6 车道、全封闭、全立交，全程有18个节点，17 个路段，限速120 km/h.收费系统中记录的旅行时间包含了车辆在收费站延误等实际行驶以外的所有时间损耗.因此，“系统记录的旅行时间”往往稍大于“实际路段旅行时间”.根据2.3 节分析，车辆行驶路程越长，延误等时间损耗在收费系统记录的旅行时间中所占的比例越小，因此可以把相距较远节点间的“系统记录旅行时间”近似作为“实际路段旅行时间”的真值.通过在相距较远的节点间，分别使用修正路段速度和原始速度采用轨迹法估计路段旅行时间，如果使用修正路段速度估计的路段旅行时间与实际路段旅行时间相对误差更小，则说明速度修正方法有效.因此，选取该高速公路上最长路段，其“系统记录旅行时间”可以作为真值来核测较长路段的路段旅行时间估计的准确性，进而对修正算法的有效性进行评价.

算例的研究路段选取该高速公路的最长路段.在数据量充足的情况下，由于每个出发时间区间的数据都经过第1 节中所述数据预处理算法的处理，可以保证任一时刻开始的时间区间内出发的车辆旅行时间数据的相似性，同时，通过对数据的分析，该高速每天车流稳定持续时段为早上7:30 到晚上8:30 左右，因此在满足每个时间区间内数据量和时间区间内旅行时间数据相似度的情况下，时间区间选定为10 min.

图5为早上7:30 到晚上8:30 每10 min 一个时间区间出发，在该条高速公路最长路段上行驶车辆实际路段旅行时间和两种估计路段旅行时间比较，其中实际路段旅行时间为ta，用估计的路段旅行时间为tb，用估计的路段旅行时间为tc.

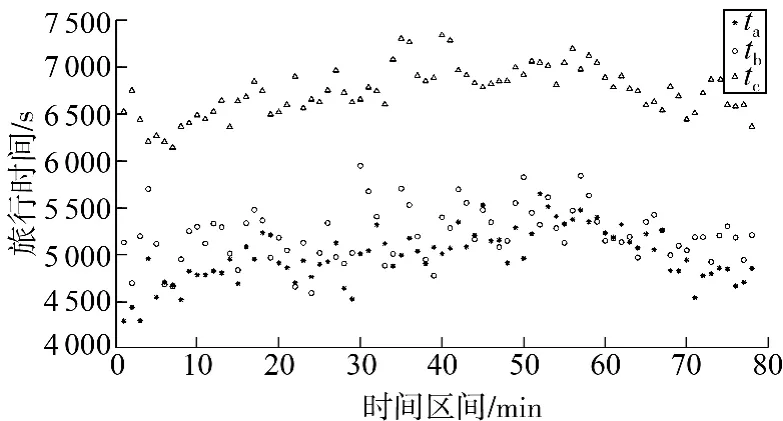
图5 实际路段旅行时间和从两种估计算法计算得到的路段旅行时间的对比Fig.5 Comparison of actual travel time and estimated travel time obtained by two methods

从图5中可以看出在绝大多数时间区间内，tb比tc更接近ta，以相对误差为评价指标:

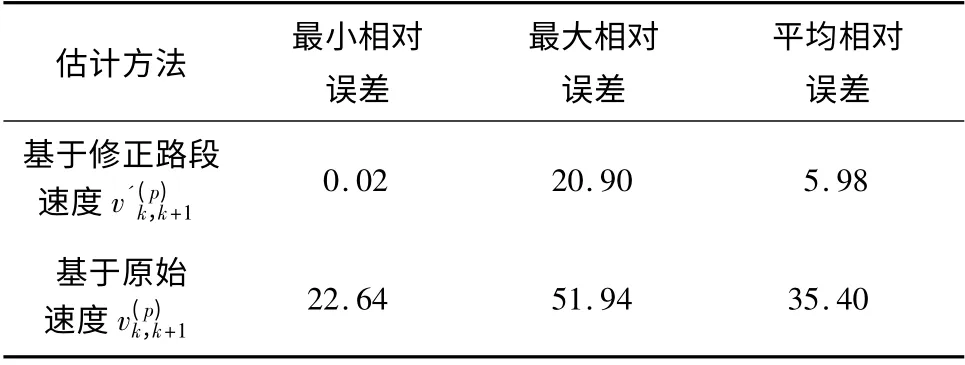
表2 基于修正速度和基于原始速度的旅行时间估计对比Table2 Comparison of estimated travel time between methods based on original speed and corrected speed %

4 结论

文中基于高速公路收费数据，提出了一种基于修正算法的路段旅行时间估计.实例证明，与基于路段原始数据计算得到的路段旅行时间相比，该改进算法计算的路段旅行时间与实际路段旅行时间误差更小，更能反映车辆的实际行驶速度.本方法可以应用在基于收费数据的路段旅行时间估计中.后续工作将进一步研究通过车辆旅行时间估计估算各路段流量，为旅行时间可靠性研究提供数据支持.

［1］Transportation Research Board.Strategic highway research program 2-reliability focus area overview，Transportation Research Board of the National Academies［DB/OL］.［2009-12-31］.http:∥www.trb.org/StrategicHighwayResearchProgram2SHRP2/Pages/Reliability_159.aspx.

［2］Cortes C E，Lavanya R，Oh J S，et al.General-purpose methodology for estimating link travel time with multiplepoint detection of traffic ［J］.Transportation Research Record，1802，2002:181-189.

［3］Dailey D J.Travel time estimates using a series of singleloop volume and occupancy measurements ［C］∥Proceedings of the 77thAnnual Meeting of the Transportation Research Board.Washington D C:［s.n］，1997.

［4］Lindveld C D R，Thijs R，Bovy P H L，et al.Evaluation of online travel time estimators and predictors ［J］.Transportation Research Record 1719，2000:45-53.

［5］Van Lint J W C，Van Der Zijpp N J.Improving a travel time estimation algorithm by using dual loop detectors［J］.Transportation Research Record，1855，2003:41-48.

［6］Shen Lu-ou，Hadi M.Practical approach for travel time estimation from point traffic detector data［J］.Journal of Advanced Transportation，2011，47(5):526-535.

［7］Nam D H，Drew D R.Traffic dynamics:methods for estimating freeway travel times in real-time from flow measurements ［J］.Journal of Transportation Engineering.1996，122(3):185-191.

［8］Nam D H，Drew D R.Analyzing freeway traffic under congestion:traffic dynamics approach［J］.Journal of Transportation Engineering，1998，124(3):208-212.

［9］Nam D H，Drew D R.Automatic measurement of traffic variables for intelligent transportation systems applications［J］.Transportation Research，Part B:Methodological，1999，33(6):437-457.

［10］Petty K F，Bickel P，Ostland M，et al.Accurate estimation of travel times from single-loop detectors ［J］.Transportation Research，Part A:Policy and Practice，1998，32(1):1-17.

［11］Coifman B.Estimating travel times and vehicle trajectories on freeways using dual loop detectors［J］.Transportation Research，Part A:Policy and Practice，2002，36(4):351-364.

［12］Hoogendoorn S P.Model-based multi-class travel time estimation［C］∥Proceedings of the 80thAnnual Meeting of the Transportation Research Board.Washington D C:［s.n.］，2000.

［13］于德新，高学英，杨兆升.基于GPS 数据及车辆运行特性分析的单车路段行程时间估计［J］.吉林大学学报:工学版，2010，40(4):965-970.Yu De-xin，Gao Xue-ying，Yang Zhao-sheng.Individual vehicle travel-time estimation based on GPS data and analysis of vehicle running characteristics［J］.Journal of Jilin University:Engineering and Technology Edition，2010，40(4):965-970.

［14］杨晓光，张汝华，储浩，等.基于高速公路收费系统的交通信息采集与处理基本问题研究［J］.系统工程，2004，22(11):4-11.Yang Xiao-guang，Zhang Ru-hua，Chu Hao，et al，Study on traffic information collecting and processing based on freeway toll system［J］.Systems Engineering，2004，22(11):4-11.

［15］王海燕，项乔君，陆键，等.高速公路出入口OD 矩阵推算方法［J］.公路交通科技，2005，22(2):108-110，115.Wang Hai-yan，Xiang Qiao-jun，Lu Jian，et al.Method of expressway ramp OD matrix calculation［J］.Journal of Highway and Transportation Research and Development，2005，22(2):108-110，115.

［16］沈强.基于高速公路收费数据的路网运行状态评价［J］.公路交通科技，2012，29(8):118-126.Shen Qiang.Road network mobility performance evaluation based on freeway toll data［J］.Journal of Highway and Transportation Research and Development，2012，29(8):118-126.

［17］Van Lint J W C.Reliable travel time prediction for freeways［M］.Netherlands:Travel Research School，2004.