考虑车辆运行特性的双车道超车模型*

许伦辉 胡三根 伍帅 罗强

(1.华南理工大学 土木与交通学院，广东 广州510640;2.广州大学 土木工程学院，广东 广州510006)

超车是公路上一种普遍的交通现象.当车道前方车辆速度小于后车速度，且相邻车道上有足够超车空间，则后车会采取借用相邻车道来完成超车过程，以追求最大驾驶效益.近些年，我国因超车不当引发的交通事故呈明显上升趋势，尤其是在高速公路上，60%以上的交通事故都与超车有关［1］.因此，对超车模型研究不仅可为道路安全超车提供理论指导，有效提高道路通行能力和服务水平，更可以降低由于不合理超车所引起的交通事故的发生率.

目前，有关超车模型研究方法国内外有很多.Worrall 等［2］运用所采集的数据分析了多车道车辆换道行为，提出车辆换道方式和频率与道路和交通状况等因素有关.Rilett 等［3］论证了车辆安全超车与车辆加速、减速及安全距离等因素之间的关系.而国内主要研究方法有元胞自动机的方法［4］和建立微分方程求解的方法［5］，但这些方法都过于繁琐，而且不能给出超车车辆与被超车辆在超车过程中的速度与时间的关系表达式.薛国新等［6-7］采用固定支梁挠度曲线模拟了高速公路的超车过程，虽然模型能计算出两车辆的实时速度和位置大小，但由于假设换道时间T 为常数，使得模型与实际超车现象不符.后来，唐铁桥等［8］在薛国新等人建立的模型基础上，提出了一种考虑换道过程中可能存在的延滞时间、车辆跟驰时的安全距离和超车过程中两车所行驶的路程之间的关系模型，还提出了双车道双向行驶的车辆超车模型.

虽然上述的研究成果对车辆超车行为给出了定性与定量的分析，但很少有学者对超车车辆的类型进行划分，且对超车过程车辆速度及加速度变化也研究得甚少.王润琪等［9］对超车过程进行考虑，将超车类型分为小汽车与普通货车两种类型，车辆间安全距离都取相同的车头间距D0，车辆分类与车头间距计算过于简单.文中在现有模型的基础上，以车辆运行特性为标准对车辆分类，且依据车辆动力特性进行参数选取，并考虑不同车道限速条件，最终建立超车车辆从超车行为产生到超车结束所需的超车时间和距离的计算模型，并论证了超车时间和距离与超车车辆类型及自身速度、被超车辆速度和对向车辆速度有关，模型更符合实际超车现象.

1 双车道车辆超车情形分析

为更好地分析车辆超车行为，以期建立更切实际的超车模型.首先对车辆在超车行为产生到超车过程结束这一过程中各车辆运动位置关系进行描述，如图1所示.

从图1可知，超车车辆为F，被超车车辆为L，实线车表示超车行为发生前车辆起始位置，虚线车表示超车过程中和超车过程结束时两车辆行驶位置.为保证车辆F 能顺利完成超车过程，应满足以下几点条件:

(1)超车前，超车车辆F 与被超车辆L 应有足够的安全车头间距，以防止被超车辆突然减速或紧急制动时发生追尾碰撞或斜向碰撞;

(2)超车结束后，被超车车辆L 与超车车辆F之间应有足够的车头间距，以防止超车车辆突然减速或紧急制动时发生追尾碰撞或斜向碰撞;

(3)超越车在超越过程中，行驶距离要大于被超越车在原车道行驶距离与相关的安全间距及车辆长度之和;

(4)超车过程中，超车车速要满足超车道的限速条件.

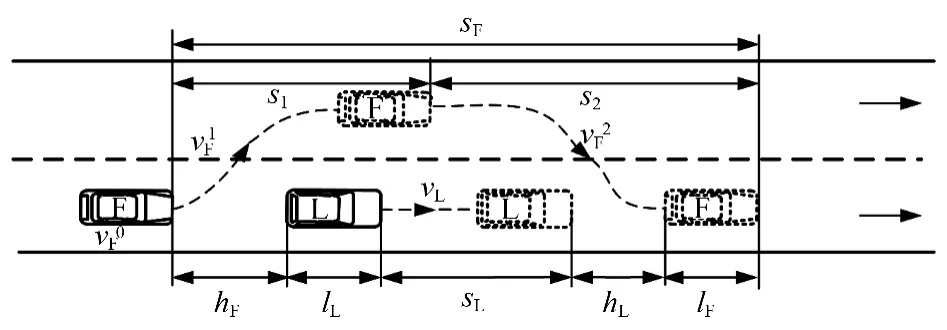
图1 超车前与超车后的前后车辆位置关系Fig.1 Positions of the following vehicle and leading vehicles before and after overtaking

根据上述几点条件，超车车辆在超车过程中所行驶的距离应满足如下关系式:

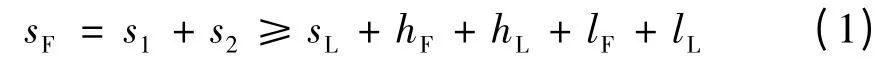
式中:sF为超车车辆F 在整个超车过程中所行驶的距离;s1为超车车辆F 加速换道行驶距离;s2为超车车辆F 匀速并道行驶距离;sL为被超车辆L 所行驶的距离;hF、hL分别为车辆间最小跟驰安全间距.lF、lL分别为超车车辆F 和被超车辆L 的长度.

2 双车道车辆超车建模与分析

2.1 车辆类型分类

众所周知，不同车辆的运动特性是不相同的，即车辆的加速性能、制动性能及车辆自身的大小完全不一样.目前，公路上所行驶的车辆不仅只有小汽车，小客车、中型车、大型车及全挂车也占据了一定的比例，因此对上述这些车辆的超车行为进行分析有重要意义.以往的车辆超车模型很少以车辆类型进行单独研究，主要是以小汽车为主要研究对象.由于车辆之间性能差异较大，以小汽车为例所建立的超车模型并不适用于其他类型车辆，尤其在混合交通流情况下，研究各类车辆的超车模型更有实际意义，更能提高道路交通安全性.

针对以往公路中车辆分类以车辆轴距为标准，造成车型偏多、分类重心与实际不符等问题，荣建等［10］提出以车辆运行特性为分类标准，并结合考虑车辆结构特征和轴距出现频率的分类方法，将公路中运行的车辆分为微型车、小客车、大中型车和不定型车4 种.因为不定型车所占比例不超过5%，因此文中只讨论前3 种车型.在公路中各车型的描述见表1.表2为上述3 种车型的车辆相关特性，车辆行驶最大加速度［11］及期望车速［12］见表2.

表1 以车辆运行特性划分的车辆类型Table1 Vehicles classified by vehicle running characteristics

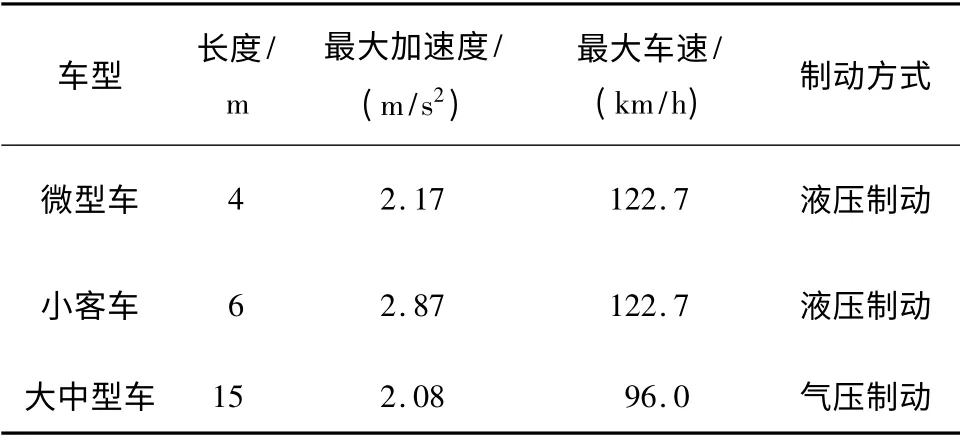
表2 各类车型特性Table2 Vehicles dynamics performance

2.2 双车道单向行驶车辆建模分析

如图1所示，超车车辆F 若要保证安全超越车辆L，超车车辆F 在超车过程中所行驶的距离要满足关系式(1).超车车辆F 的超车过程可以分为2个阶段:

(1)加速换道阶段.换道开始超车车辆F 以初始速度v0F加速到超车速度v1F(v1F＞vL)，加速度为a.此段行程时间为t1，行驶距离为s1.

(2)匀速并道阶段.超车车辆F 以超车速度v1F匀速行驶到原车道，完成一次超车过程.此段行程时间为t2，行驶距离为s2.

上述2 个阶段总的行程时间为t:

式中

超车车辆F 总的行驶距离为sF，

s1，s2分别为

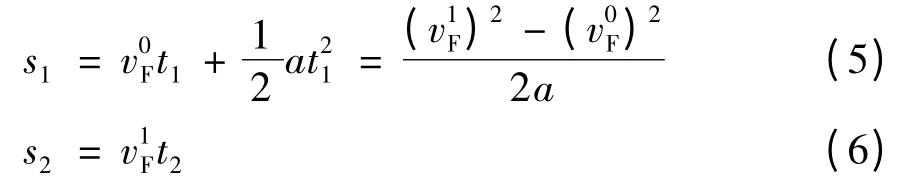
被超车辆L 总的行驶距离sL为

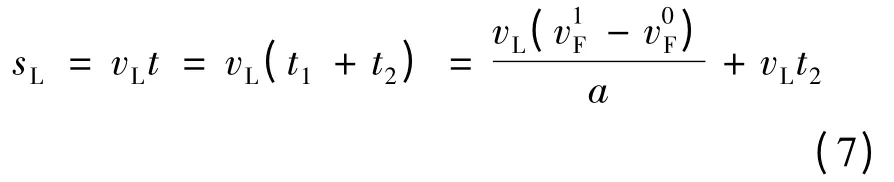
将式(5)-(7)代入式(1)可得:

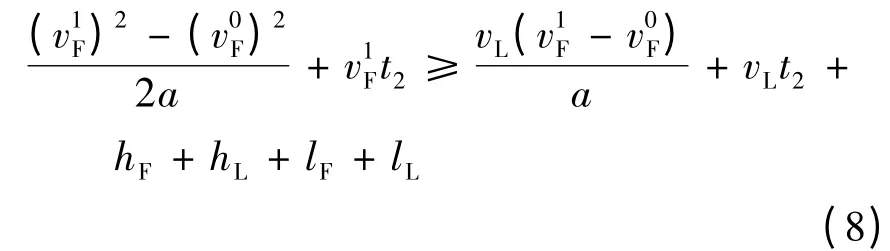
由式(8)可求得t2，即:

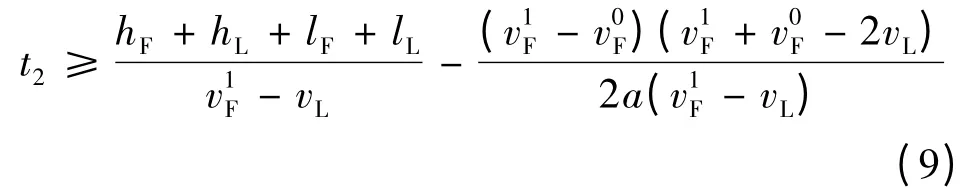
由式(3)、式(9)可求得总的超车时间t:

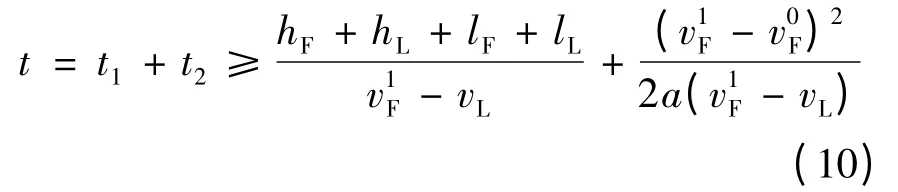
式中，hF为车辆F 跟驰时与车辆L 所需最小安全间距.为保证足够安全，文中只考虑被超车辆L 突然停车时，车辆F 与车辆L 所必须保持的最小行车间距.则

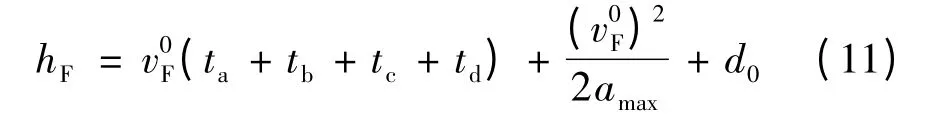
同理，

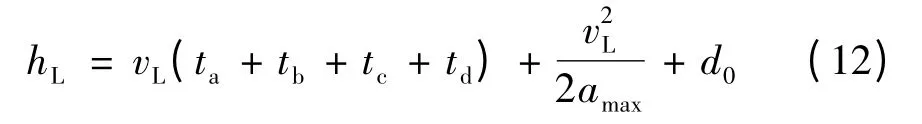
式中:ta为驾驶员反应时间，tb为驾驶员将右脚从加速踏板移动到制动踏板的时间，ta+ tb一般取值为0.8 ～1.3 s;tc为制动协调时间，即驾驶员踩下制动踏板到消除制动装置的间隙和弹性所需时间，一般取值0.2s［13］;td为制动力增加时间，它一方面取决于驾驶员踩制动踏板的速度，另外更重要的是受车辆制动方式的影响，驾驶员急速踩制动踏板时，液压制动系td为0.15 ～0.20s，真空助力和气压制动系td为0.3 ～0.9 s［14］;amax为车辆F 最大加速度，它的大小主要跟路面的附着系数有关，满足如下关系式:

式中:g 为重力加速度，取值9.8 m/s2;f 为路面附着系数，一般在0.2 ～0.8 之间［15］;d0为安全裕量，一般取值范围在2 ～5 m.

综上所述，超车车辆F 在超车过程中所行驶的距离为

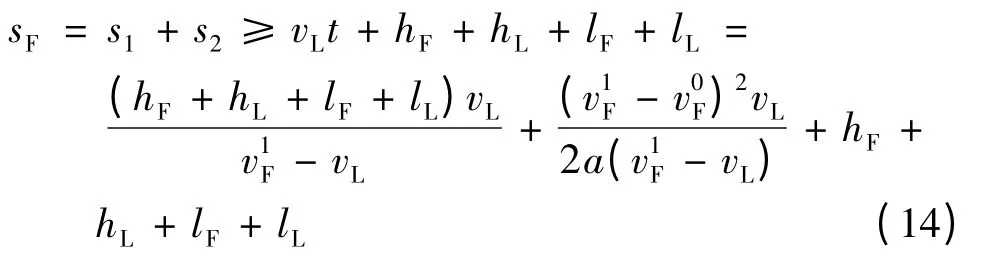
2.3 双车道双向行驶车辆超车建模

目前，国内存在很多双车道公路，同方向仅只有一个车道.由于道路中行驶的车辆种类比较多，车辆之间速度大小不一，在此情况下，很容易发生车辆借助对向车道进行超车.为了保证车辆能顺利借助相邻车道超越前车并安全驶回原车道，而不与对向车道驶来的车辆发生正面碰撞，超车车辆在此过程中所行驶的安全距离称为最小超车距离，也称超车视距［16］.视距是指驾驶人从车内能看到该车道前方中心线上障碍物高(0.1 m)处的可见长度［16-17］，即超车前超车车辆与对向车道车辆之间的最小距离，也称为车流空隙长度.若超车前超车车辆与对向车道的车辆之间距离小于最小超车视距，此时超车可能会导致交通事故发生;相反，则可以安全超车.

图2为双车道双向行驶车辆超车情形，并给出各车辆之间的时间-位置关系，由此可以计算出超车车辆所需的最小超车视距.不考虑对向车辆O 的行驶速度受超车车辆的干扰，即在整个超车过程中，对向车辆的速度保持稳定.为保证车辆F 与车辆O绝对不发生碰撞，车辆F 安全驶回原车道后与车辆O 间隔hF+ hO距离，此时若不发生碰撞，车辆F 并道过程就不会与车辆O 发生碰撞.

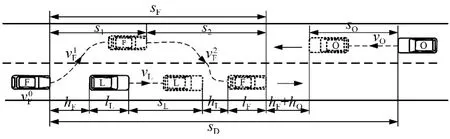
图2 双向双车道超车示意图Fig.2 Overtaking scheme in a two-lane bidirectional traffic flow

根据前文分析可知，对向车辆O 在整个超车过程所行驶的距离sO为

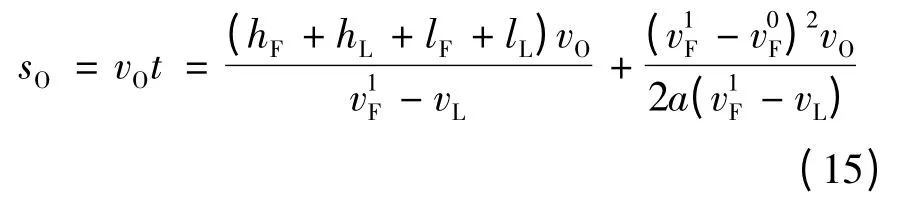
因此，在此情形下超车车辆F 安全超车所需的最小超车视距sD为

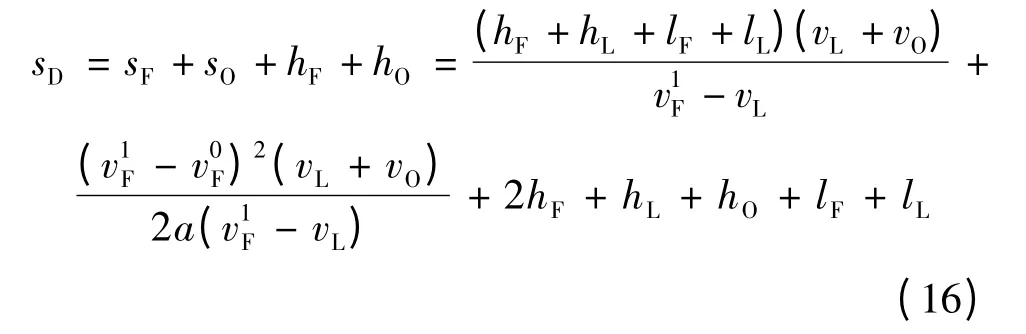
式中，hO为车辆O 减速至停车所行驶的距离，计算公式为

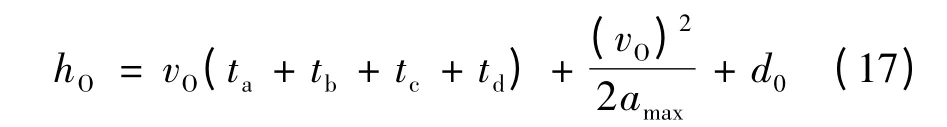
其他变量含义同前.

3 双车道单向行驶超车模型数值分析

为保证模型的实用性和计算结果的可靠性，在模型数值分析前需对相关前提条件作以下说明:

(1)加速度a 取常值.为了说明文中超车模型与车辆运行特性有关，同时也为保证能与唐-黄模型在相同建立条件下(匀加速超车)进行数值结果对比分析，文中只针对超车加速度a 为常数的情形给出模型数值分析.而对于变加速超车(a 时变)的复杂情形，需有待进一步研究.

(2)为使模型计算结果更符合实际超车现象，文中模型数值分析都是基于不同车辆运行特性及不同道路等级的设计时速等前提下给出.

(3)引入的唐-黄模型给出的计算结果都是基于与文中模型数值计算的相同前提条件下得到的，确保两者模型计算结果具有可对比性.

3.1 超车时间与车辆类型关系

由式(10)可知，最小超车时间和车辆F 的超车速度v1F与被超车辆L 的速度vL两者差值v1F- vL大小及车辆F 超车时的加速度大小相关.若车辆L 速度vL很大，超车时间也会相应增大，超车过程会变长;反之，超车时间会减小，很快完成超车.若车辆F加速度a 越大，加速到超车速度v1F的时间就越短，整个超车时间也随之减小.显然，超车时间计算公式与实际超车现象相符.

为保证超车过程足够安全，ta+tb取值为1.2s，tc取值为0.2s，d0取值为5m.根据文献［15］规定，计算超车时间与超车距离在潮湿路面下取值，即f 取值为0.5，amax为4.9 m/s2.现以3 种类型车辆分别超越不同速度的小客车情形为例，来分析不同车辆完成超车时花费的时间与v1F- vL大小之间的关系，并假设车辆F 初始速度v0F为70 km/h，车辆L 初始速度vL也为70km/h.图3为3 种类型车辆超越前车所需的最小超车时间与v1F- vL大小之间的关系曲线.图4为唐-黄模型的最小超车时间与v1F- vL大小之间的关系曲线.

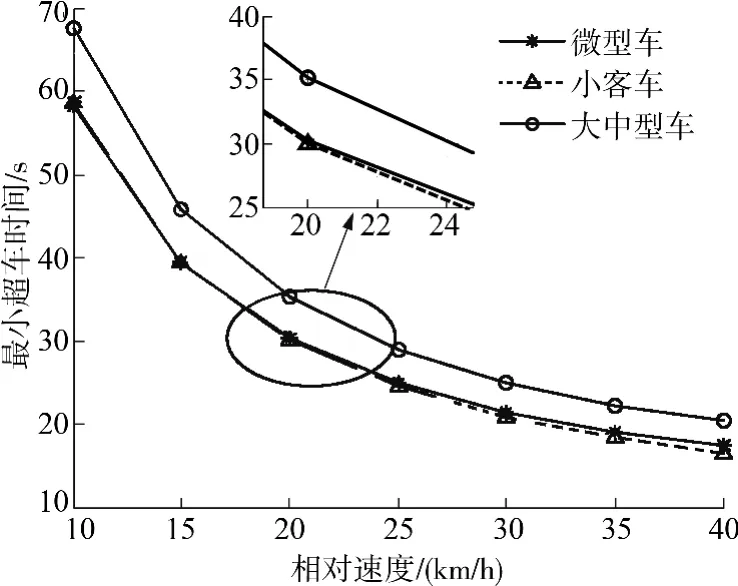
图3 不同类型车辆超越小客车时的最小超车时间Fig.3 Plot of minimum overtaking time of kinds of vehicles overtaking mid-size cars

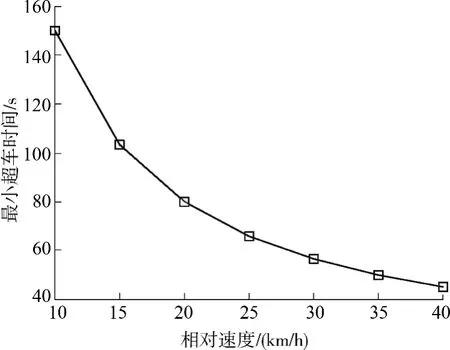
图4 唐-黄模型的最小超车时间与相对速度关系Fig.4 Plot of minimum overtaking time versus relative speed obtained by Tang-Huang model

对比图3与图4中的曲线可知，在超车过程中，文中所求得的最小超车时间远小于唐-黄模型所计算出的超车时间，且不同车辆超车所需的最小超车时间也不相同，究其原因是由于文中考虑了车辆在超车过程中不同车辆运行特性.又因为中大型车的加速度和最大行驶速度都要小于微型车与小客车，超车相对后者两种车型更为困难，超车时间也相对会长些，这与实际超车情况相吻合.

3.2 超车距离与车辆类型关系

车辆F 完成一次超车过程，所行驶最小超车距离可由式(14)求得.从式(14)中可以得出，超车距离与超车速度v1F、被超车辆速度vL及超车车辆加速度a 相关，如果被超车辆L 的速度vL很大，超车距离会很长，很难快速完成超车;如果车辆F 与车辆L的速度相等，即v1F-vL= 0 ，则车辆F 的超车距离sF会趋向无穷大，无法超车;如果车辆F 换道加速度a越小，超车距离也会变大.因此，超车距离计算公式能很好地反映不同车辆行驶过程中的实际超车现象.

仍以3 种不同类型车辆分别超越不同速度的小客车情形为例，来计算不同车辆超车时所行驶的超车距离，计算结果如表3.考虑到不同等级公路不同车道限速条件，超车车辆的超车速度v1F取道路设计时速，超车车辆的初始速度v0F取值与被超车辆行驶速度vL相同，因为引起超车的分界条件是被超车辆行驶速度小于或等于超车车辆的行驶速度［9］，其他参数取值同上.

由表3可知，超车距离会随着被超车辆速度增加而增大，且在相同的超车环境下，不同类型车辆超车距离也会不一样.由表3可知，超车车辆以超车速度80 km/h 安全超过行驶速度为50 km/h 的被超车辆，所需的超车距离为303.50 m，超车时间为14.38 s，超车较为容易.当被超车辆速度提高到60 km/h，所需的超车距离猛增到541.43 m，超车时间为24.68 s，超车困难;这是因为被超车辆的速度越接近超车车辆的超车速度，超车车辆越需要更长时间和超车距离才能完成超车.又例如，当被超车辆行驶速度为50 km/h，超车车辆超车速度由60km/h 增大到80km/h 时，超车距离从631.77m 突降到303.50m，超车时间从38.01s 减少到14.38 s.因此，当被超车辆速度一定时，在满足道路限速条件下，超车车辆适当增加超车速度，可以有效减少超车时间和超车距离，缩短超车过程，减少车辆发生碰撞的可能性.同理，对于小客车和大中型车，由表3可得到同样结论.另外，从表3中可知唐-黄模型所计算出的超车时间和超车距离都比文中建立的模型计算值要大，且不同类型的车辆超车时间和超车距离都相同，显然与实际不符.

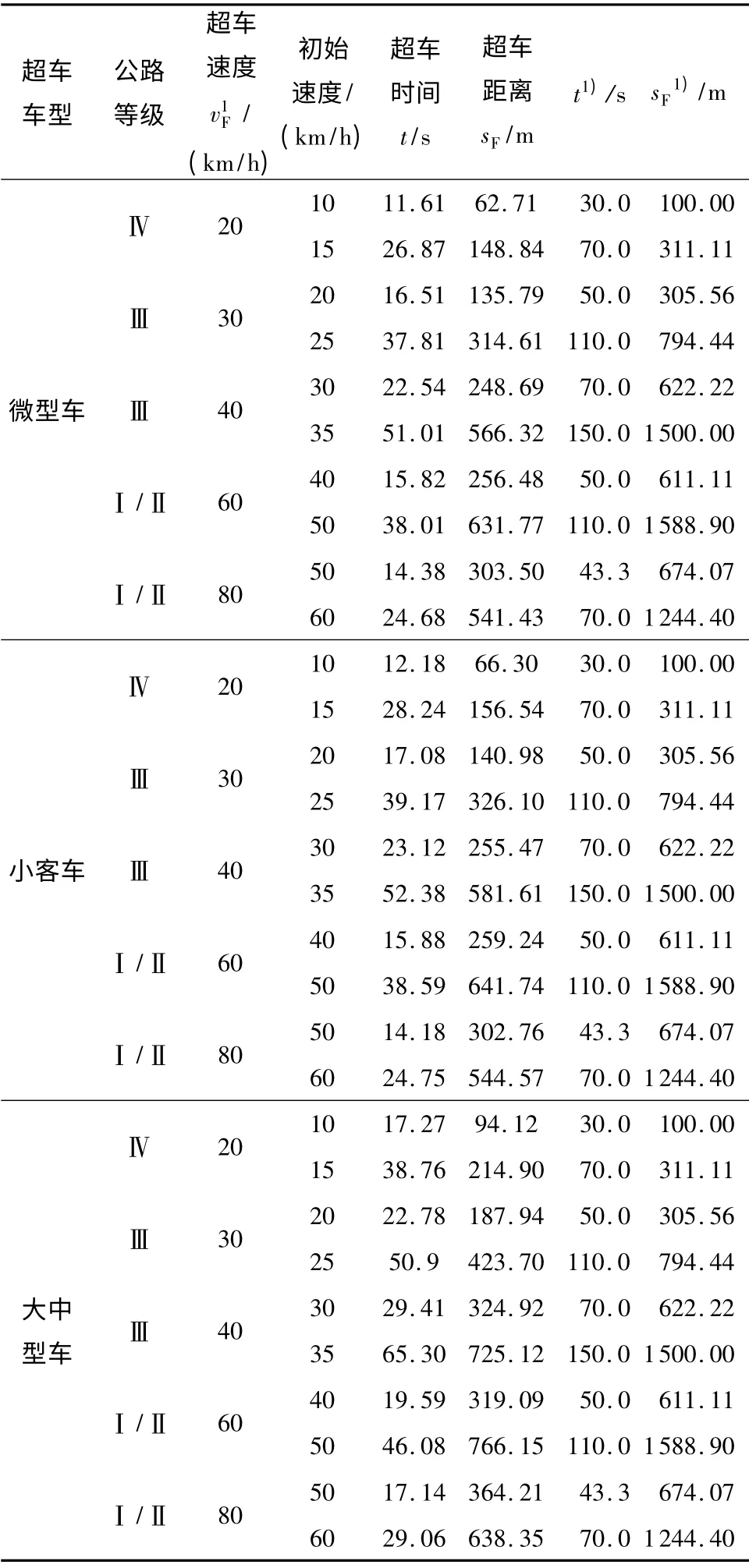
表3 单向双车道微型车、小客车、大中型车超车距离计算值Table3 Calculated values of micro cars、mid-size cars and fullsize cars overtaking distances for two-lane highway

4 双车道双向行驶超车模型数值分析

同样以3 种不同类型车辆分别超越不同速度的小客车情形为例，并假设对向车辆O 也为小客车来计算不同车辆借助对向车道超车时所需的最小超车视距.根据公路相关设计规范，Ⅰ级公路采用分向分道行驶，不存在借助对向车道进行超车现象，因而只对Ⅱ、Ⅲ、Ⅳ级公路超车时间与超车视距进行计算.由于考虑到模型的真实性，对向车辆O 的行驶速度不宜过大，否则超车车辆不能及时借助对向车道完成超车，势必会需要很长的超车视距才能保证安全超车，而且在该种情况下不存在超车的可能，其他参数设定同上文所述.不同情形下的超车时间与超车视距计算结果如表4所示.

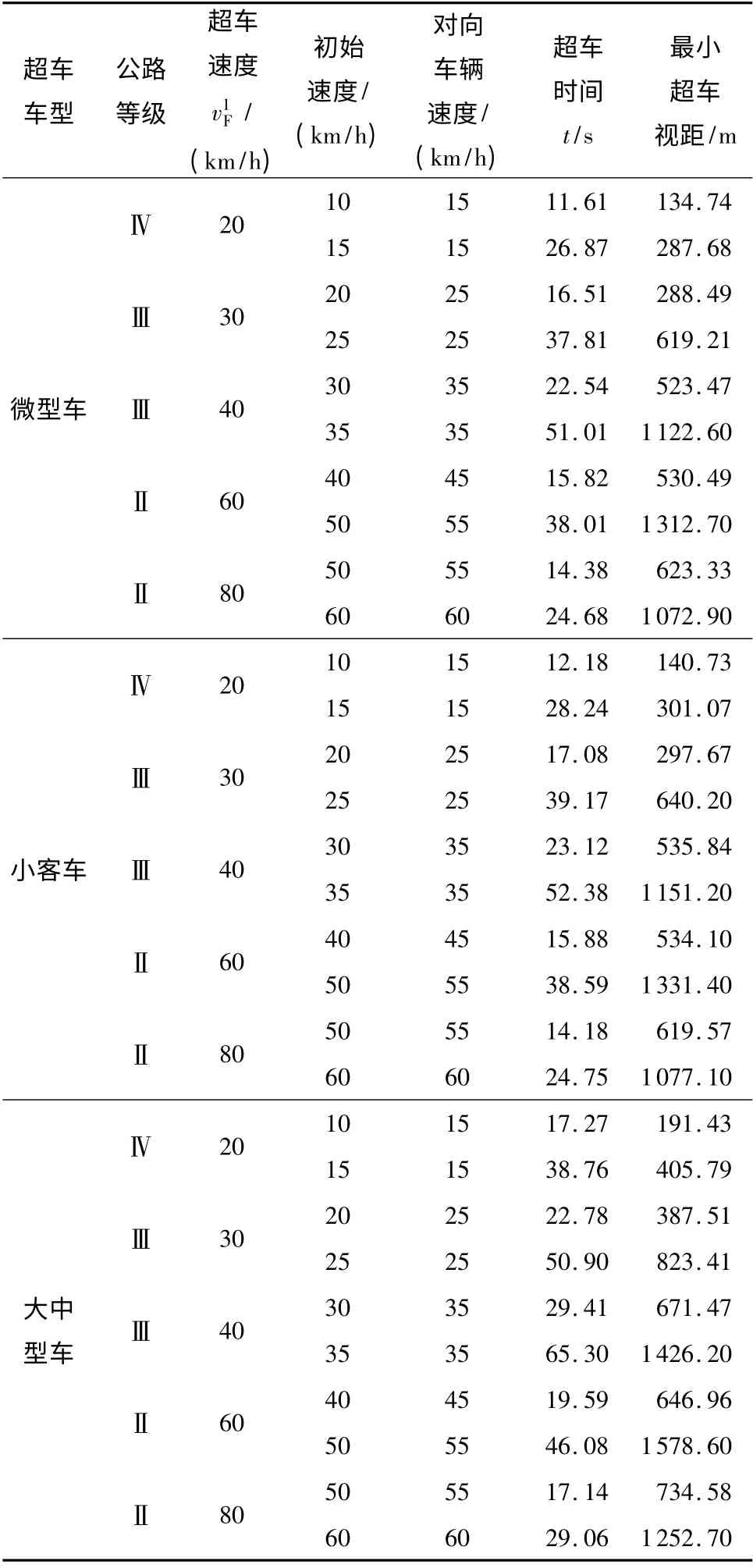
表4 双向双车道公路上微型车、小客车、大中型车超车视距计算值Table4 Calculated values of micro cars、mid-size cars and fullsize cars overtaking sight distances for two-lane bidirectional highway

由表4中超车时间和超车视距计算值可知，若车辆F 安全超越前车时，车辆F 与对向车辆O 之间距离要大于表中所对应的最小超车视距，否则不能安全超车.从表中数据还可以得出，超车时间和超车视距会随着被超车辆L 和对向车辆O 的速度增加而增大，不同类型车辆超车所花费的超车时间和最小超车视距会不同，大中型车超车时间和最小超车视距显然都大于微型车和小客车.由表4可知，当超车速度为60 km/h，被超车车辆为40 km/h 和对向车辆速度为50 km/h 时，微型车完成超车过程所花费的时间为15.82 s，最小超车视距为530.49 m，能很快完成超车;若被超车辆速度提升到50 km/h，且对向车辆O 的速度为55 km/h 时，微型车完成超车过程所花费的时间增长到38.01 s，最小超车视距迅速增大到1312.7 m，超车过程迅速变长，超车相比前种情况更为困难.另外，当被超车辆速度为50km/h，对向车辆速度为55 km/h 时，车辆F 超车速度从60 km/h增加到80 km/h时，最小超车视距从1312.7 m减少到623.33 m，超车时间从38.01 s 减少到14.38 s，有效缩短了超车视距和超车时间.因此，在路况条件较好的情况下，超车车辆可以适当提高超车速度，可以减少所需的超车时间和最小超车视距，快速完成超车过程.同理，对于小客车和大中型车，由表4中数据可以得出相同结论.

综上所述，由文中建立的超车模型所得到的超车时间和最小超车视距，均与超车车辆自身行驶速度和超车速度与被超车辆速度两者差值以及与车辆类型(最大加速度不同)密切相关.

5 结语

文中在对文献中现有超车模型研究的基础上，以车辆运行特性作为车辆分类的首要标准，并结合考虑车辆的轴距出现频率和结构特征，对超车车辆进行细致分类，设计了不同类型车辆双车道超车场景，并考虑不同道路的等级情况(车道数、设计时速)，从而建立了计算超车车辆从超车行为产生到超车过程结束所需的超车时间和距离的数学模型，有助于车辆进行超车行驶时提供判断与辅助决策，尤其对建立智能车辆超车辅助驾驶系统能提供理论依据，即当实际超车视距小于模型所计算的理论值，辅助系统给予预警并改变当前行驶状态，保证车辆行驶的安全.另外，也可为路况条件较差、车辆速度较大或车辆密度较大等路段是否设置超车禁止标志提供参考和借鉴.对于超车过程中的加速度变化及模型变量取值等还有待进一步研究.另外，超车过程中驾驶员的心理承受度和换道舒适性尚未考虑.

［1］Kretschmer M，Neubeck J，Wiedemann J.Combining vehicle dynamics control and decision making procedures towards safe overtaking maneuvers［J］.SAE Technical Paper Series，2005，7(12):408-412.

［2］Worrall R D，Bullen A G R.An empirical analysis of lane changing on multilane highways ［J］.Highw Res Rec，1970，303:30-43.

［3］Rilett L R，Hutchinson B G，Whitney M.Mechanics of the passing maneuver and the impact of large trucks ［J］.Transportation Research，Part A，1990，24(6):121-128.

［4］薛郁，董力耘，戴世强.一种改进的一维元胞自动机交通流模型及减速概率的影响［J］.物理学报，2001，50(3):445-449.Xue Yu，Dong Li-yun，Dai Shi-qiang.An improved one-dimensional cellular automation model of traffic flow and the effect of deceleration probability［J］.Acta Physica Sinica，2001，50(3):445-449.

［5］邹智军，杨东援.交通仿真系统中的纯微观跟车模型［J］.同济大学学报，2001，29(8):899-902.Zou Zhi-jun，Yang Dong-yuan.Pure-micro car following model for traffic simulation system［J］.Journal of Tongji University，2001，29(8):899-902.

［6］薛国新，顾怀中.用固支梁挠度曲线模拟高速路基本超车过程［J］.力学与实践，2003，25(6):31-32.Xue Guo-xin，Gu Huai-zhong.Modeling basic overtaking process on a high-way with the deflection curve of a beam with fixed ends［J］.Mechanics in Engineering，2003，25(6):31-32.

［7］薛国新，顾怀中.高速公路交通流问题的分段固支梁计算机仿真模型［J］.系统仿真学报，2003，15(12):1796-1798.Xue Guo-xin，Gu Huai-zhong.Simulating traffic flow of a highway with segment fixed-end-beam model［J］.Journal of System Simulation，2003，15(12):1796-1798.

［8］唐铁桥，黄海军，梅超群.一种改进的超车模型［J］.交通运输系统工程与信息，2005，5(4):23-25.Tang Tie-qiao，Huang Hai-jun，Mei Chao-qun.An improved overtaking model ［J］.Journal of Transportation System Engineering and Information Technology，2005，5(4):23-25.

［9］王润淇，周勇君，肖传恩.双车道公路超车视距计算方法［J］.交通运输工程学报，2011，11(3):68-73.Wang Run-qi，Zhou Yong-jun，Xiao Chun-en.Calculation method of overtaking sight distance for dual highway［J］.Journal of Traffic and Transportation Engineering，2011，11(3):68-73.

［10］荣建，刘小明，任福田，等.基于高速公路通行能力分析的车辆分类研究［J］.中国公路学报，1999，12(3):82-89.Rong Jian，Liu Xiao-ming，Ren Fu-tian，et al.Vehicle classification for expressway capacity analysis［J］.China Journal of Highway and Transport，1999，12(3):82-89.

［11］Satish Chandra，Shalinee Shukla.Overtaking behavior on divided highways under mixed traffic conditions ［J］.The 8thInternational Conference on Traffic and Transportation Studies，2012，43:313-322.

［12］刘震，符锌砂.基于人-车-路综合影响的期望速度研究［J］.中外公路，2010，30(1):41-43.Liu Zhen，Fu Xin-sha.Research on expectation speed on integrate affects of driver-vehicle-road ［J］.Journal of China ＆ Foreign Highway，2013，30(1):41-43.

［13］胡三根.基于SPCE061A 的汽车防碰撞报警系统研究［D］.广州:华南理工大学土木与交通学院，2013.

［14］陈家瑞.汽车构造［M］.北京:人民交通出版社，2002.

［15］王润琪，蒋科军.ABS 汽车制动距离的分析与计算［J］.中南林学院学报，2005，25(2):70-73.Wang Run-qi，Jiang Ke-jun.Analysis and calculation of braking distance of ABS automobiles ［J］.Journal of Central South Forestry University，2005，25(2):70-73.

［16］ITG B01—2003，公路工程技术标准［S］.

［17］ITG D20—2006，公路路线设计规范［S］.