Pseudo-Linear Kalman Filter-based GPS Active Aircraft Tracking Algorithm

Zhimin Chen,Yuanxin Qu,Yuming Bo,Yongliang Zhang,Bo Cong,Xinfeng Yu

Pseudo-Linear Kalman Filter-based GPS Active Aircraft Tracking Algorithm

Zhimin Chen1,2,Yuanxin Qu1,Yuming Bo1,Yongliang Zhang1,Bo Cong1,Xinfeng Yu1

For the sake of a higher accuracy of active aircraft GPS tracking,the tracking algorithm based on pseudo-linear Kalman filter is hereby proposed.This algorithm simplifies geometrical and algebraic relations to obtain a pseudo-linear model,then tracking the target by means of Kalman filter algorithm.Meanwhile,the tracking algorithm is studied to build a velocity&position tracking model and a velocity&acceleration tracking model.As shown by the experimental result,the tracking algorithm based on pseudo-linear Kalman filter can meet the requirement of active aircraft GPS tracking,but also attain a higher tracking accuracy in velocity&acceleration tracking model.

Pseudo-linear;Kalman filter;GPS;Tracking model.

1 Introduction

During GPS aircraft tracking,there is a need to establish a motion model in the light of aircraft’s maneuvering characteristics and meanwhile predict target state by means of online estimation[Mosavi,Nabavi,and Nakhaei(2014);Teng and Shi(2012)].As one of the most classic prediction methods,Kalman filter algorithm carries out recursive estimation with the use of minimum mean square error,and achieves high performance in linear system[Baiden,Bissiri,Luoma,and Henrich(2014);He,Martin,and Bilgic(2014)]. Strictly speaking,however,GPS aircraft tracking algorithm is strongly non-linear.As a result,only by studying corresponding non-linear filter algorithm,will aircraft GPS tracking requirement be met[Nievinski and Larson(2014)].

Kalman filter algorithm and its improved algorithm have been studied and applied for a long time due to its simple principle and low computing amount.EKF implements non-linear estimation by means of traditional KF algorithm after the lin-earization of Taylor expansion.This algorithm carries out Taylor expansion for non-linear system equation or observation equation to figure out first-order approximate term.Consequently,it is inevitable that the linearization of non-linear problems will result in linearization errors[Zhou,Yang,and Mi(2012)].Additionally,the real-time performance of target tracking will be also influenced by the highly complex Jacobian matrix of system or observation equation.

To eliminate the deficiencies of existing algorithms,active aircraft GPS tracking algorithm based on pseudo-linear Kalman filter is presented,and the pseudo-linear model it builds has lessened the complexity of algorithm and established a tracking model by estimating the target state with KF algorithm.As revealed by the simulation experiment,the improved algorithm proposed herein has high tracking accuracy.

2 Kalman filter

Kalman filter is to estimate the optimal system state in combination with observation information and state transition rule.

Assuming the state space model of dynamic system is:

WhereX(t)stands for system state at the time oft;Y(t)for the observed value of state;W(t)for system noise;V(t)for observation noise;Φ for state transition matrix;Hfor observation matrix and Γ for driving matrix of system noise.

Below is the computing process of Kalman filter:

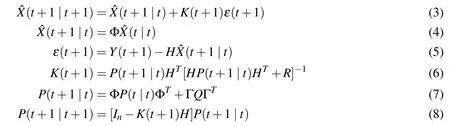
3 Pseudo-linear kalman filter

Kalman filter algorithm is derived based on minimum mean square error,and its thought is to construct the linear vector model of unknown parameters and find the solution of state vector by means of recursion under the condition of minimum error.This algorithm demands that there should be a linear relationship between the states of adjacent moments as well as between the state and the observed variable.The observation model studied herein is termed as pseudo-linear Kalman filter since the observation vector and matrix are associated with the observed variable including errors[Wang,Haynes,Huang,Dong,and Atluri(2015)].

The state transition equation is built according to different motion forms of the target,mainly including uniform motion,uniformly accelerated motion and maneuvering form[Rao and Reddy(1996);Yazdanparast and Vosooghi(2014);Liu and Ding(2011)].Assuming the state variable of uniformly moving target is(n)=the state transition equation of target motion can be expressed as follows:

Where Φ(n+1,n)=refers to state transition matrix,withbeing the unit matrix of 3×3 andTbeing the observation time interval;and(n)to the process noise of the known mean value and variance.The state variable of the target moving at uniform velocity is hypothesized as follows:

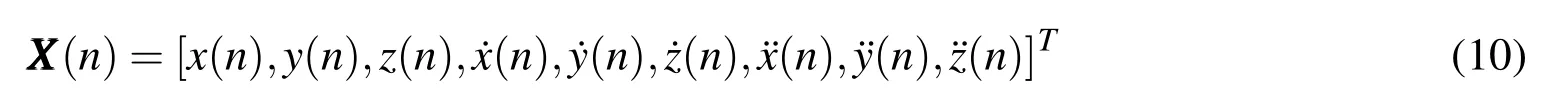
The state transition matrix of state transition equation is expressed as follows:

For the maneuvering target,there is some relationship between state acceleration and state noise[Chen,Bo,Wu,and Zhou(2013)],and different motion scenes always correspond to different tracking models.In this paper,the typical statistical model is adopted,and its state transition matrix is represented as follows:

Where,γ1=with α reflecting the maneuvering speed.

The covariance matrix of state error is represented as follows:

Where,

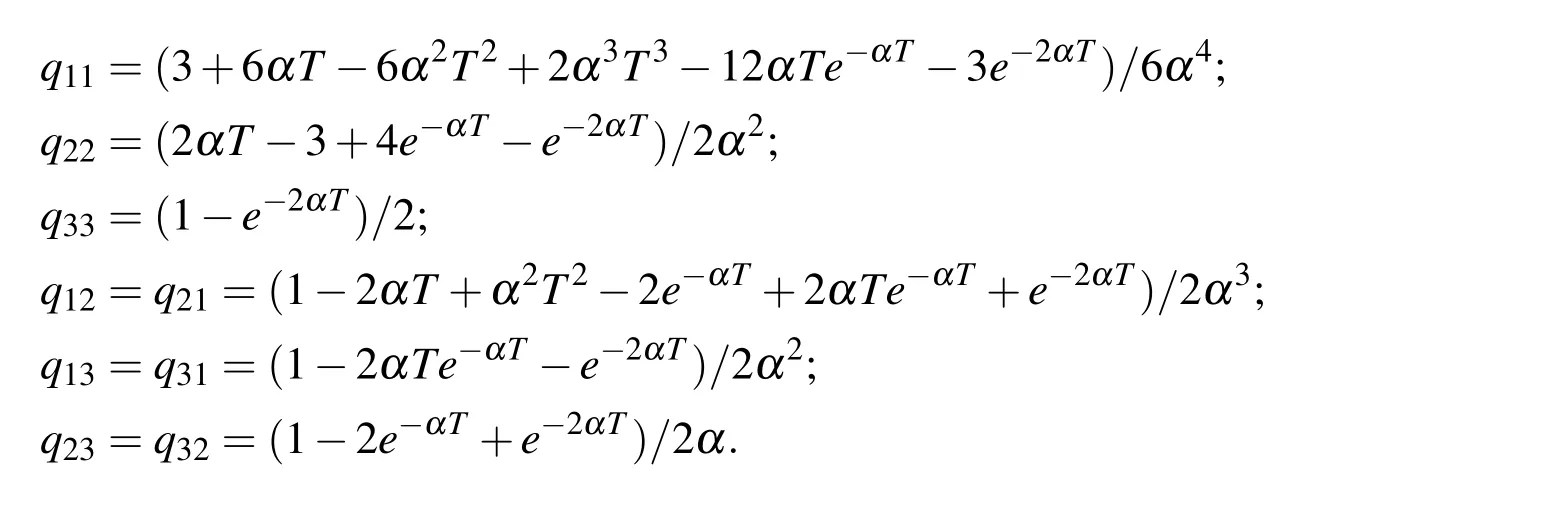
Therefore,the process equations of pseudo-linear Kalman filter in this paper are summarized as follows:

The non-linear observation equation is built as follows:

Where Θ =[θ,ϕ,τ1,...,τK]T.Here,the initial moment is analyzed and the differential treatment for both sides of the equation is conducted:

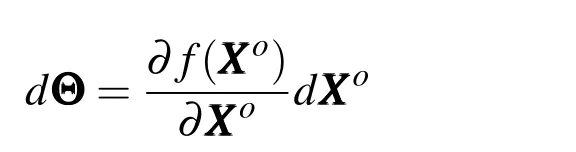
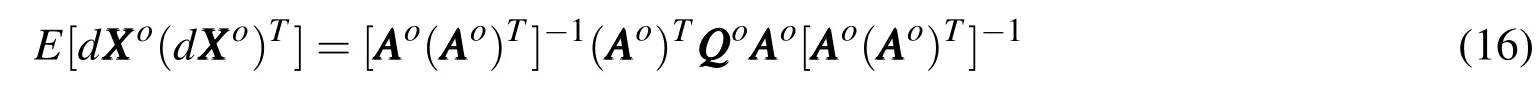
Wheremeans the covariance matrix of velocity and acceleration errors at initial moment.Considering it is difficult to figure out the theoretical value,an initial value=6is given:

The filter algorithm begins,withn=1,2,3,...

Since target state involves not only target position but also target velocity and acceleration,the observation matrix of the target should be transformed according to different motion models.For the uniform motion model,the observation matrix isand for uniformly accelerated motion and maneuvering model,the observation matrix isBelow is the computing process of gain matrix:

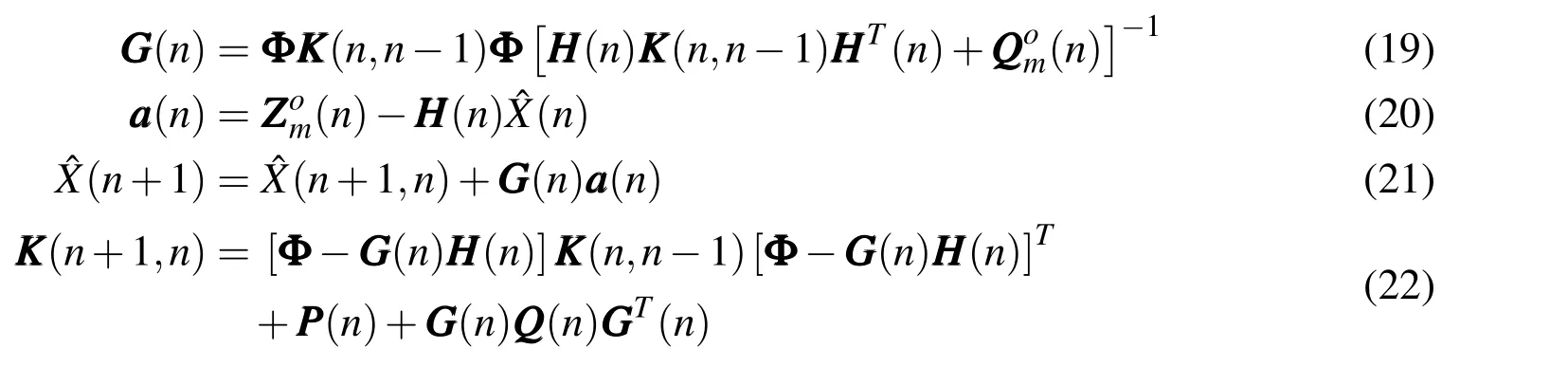
4 Tracking model

In filter,dynamic model is completely determined by two matrix parameters:

(1)Dynamic coefficient matrixF;

(2)Dynamic perturbation variance matrixQ.

The matrix parameters of two different aircraft dynamic models are shown in table 1,in which the parameter values are constant and so is the state transition matrix Φ:

The independent parameters of the models can be fixed by filter.Since system model is time-invariant,the limited dependent variables are determined by the Riccati differential equation of steady matrix,namely:

Only when the characteristic value ofFlies in the left half of complex plane,will there be a solution to the equation.Surely,even if the Riccati differential equation of full matrix lacks finite solution,the reduced equations of the sub-matrix withP∞and correspondingF’s sub-matrix will still have a finite and stable solution.

4.1 Velocity&Position model(V&P model)

V&P model can estimate the three-dimensional position and velocity.In the active aircraft dynamic model,the tracker will face changes in zero-mean white noise acceleration,unbounded steady-state velocity,and unbounded steady-state position.In case of the loss of GNSS signal,the uncertain velocity changes will be increased in finitely unless corresponding measures are taken,such as,restricting velocity changes to a certain maximum value.The tracker based on this model can work efficiently in the presence of GNSS signal.

The complete model is comprised of three position components and three velocity components,and the three-dimensional V&P model has a need for the filtering parameters as follows:

4.2 Velocity&Acceleration model(V&A model)

This model also contains the time-dependent constant of acceleration τa,which is conducive to differentiating between the models with different maneuvering characteristics.Nevertheless,there will be a difficulty in finding a solution by means of closed formula if the model is seen as the steady-state equation of RMS velocity and acceleration functions.

The sub-matrix of state transition matrix Φ in relation to velocity and acceleration along a single axis is expressed in the form as follows:

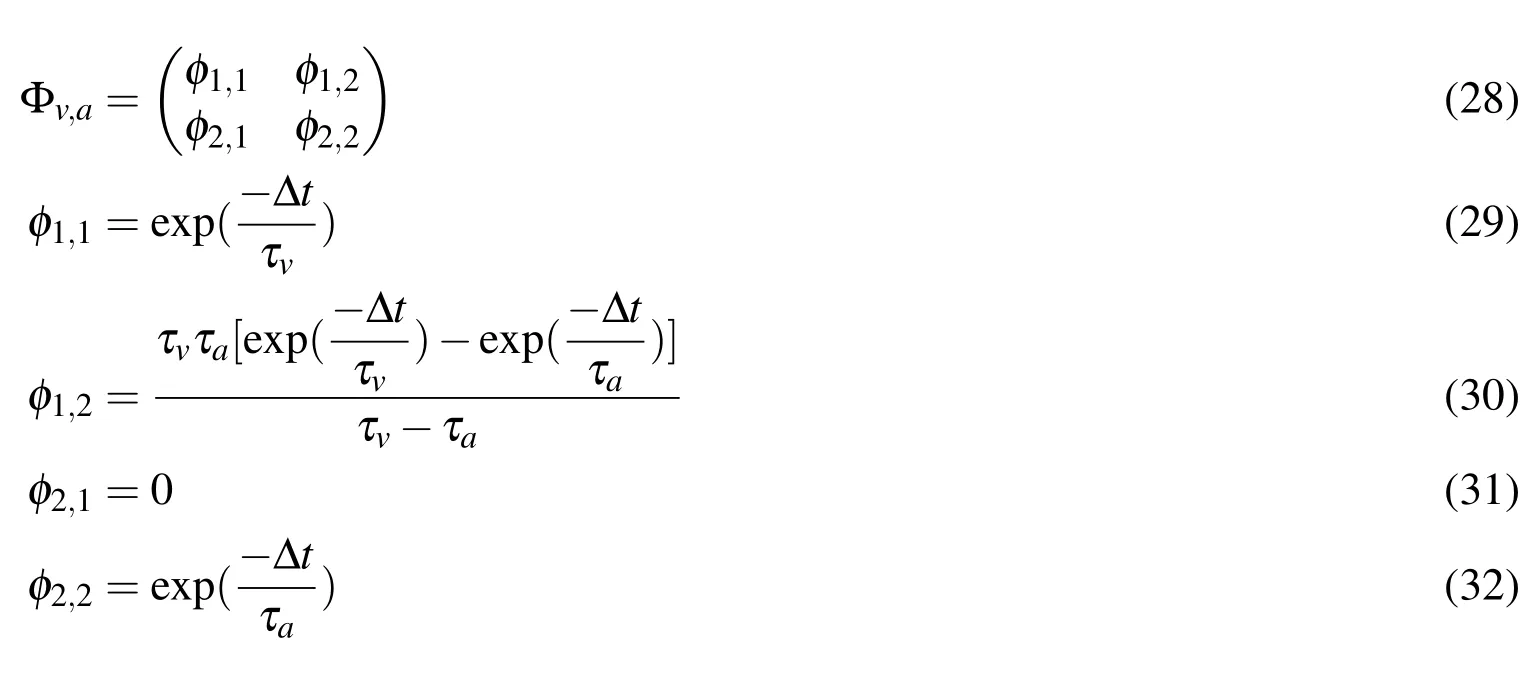
Sub-matrix ofQis represented as follows:

Corresponding RICCATI equation can be used to find a solution for following equation:

Steady-state RICCATI equation can be utilized to find a solution for the correlation coefficient between velocity and acceleration components;that is,

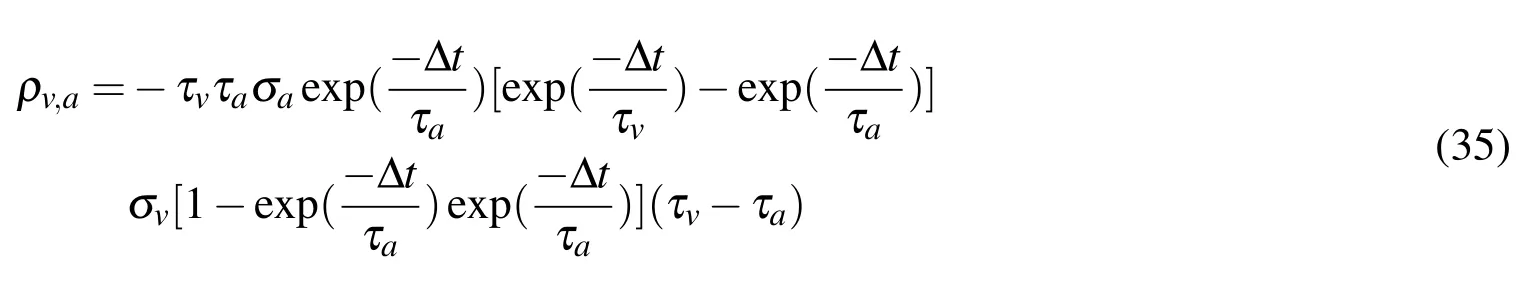
Since the surplus element of the independent variable τvin RICCATI equation is 0,it is necessary to find a solution for the transcendental equation.

5 Experimental simulation

The velocity is 35m/s;the tracking length is 1000mand the satellite number is 29,crossover height is 15m,RMS position uncertainty is 52.0,RMS pseudo range uncertainty is 20,RMS pseudo range measurement white noise is 20,correlation time-constant of pseudo range errors is 90.

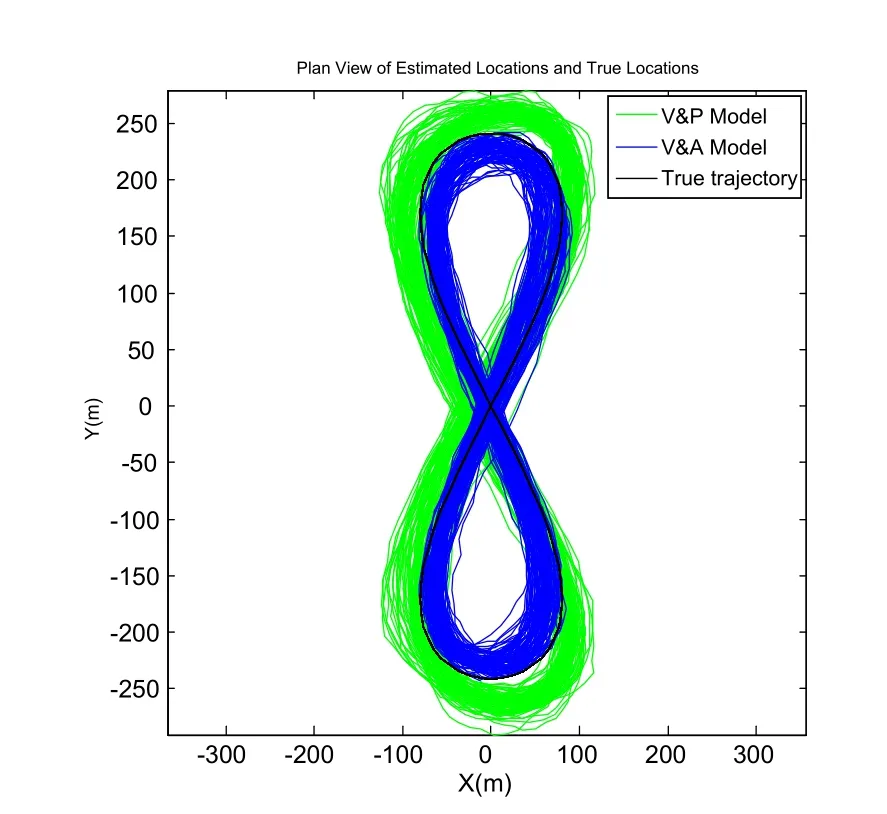
Figure 1:Tracking trajectory of CH model and C model.

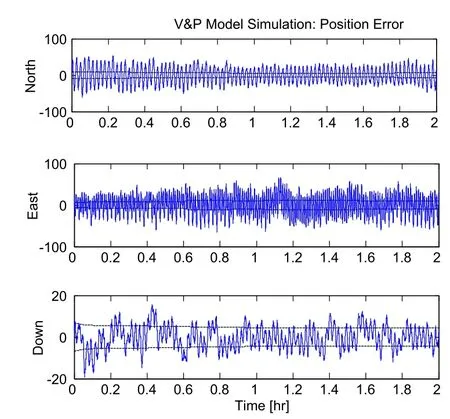
Figure 2:Position error of V&P model.

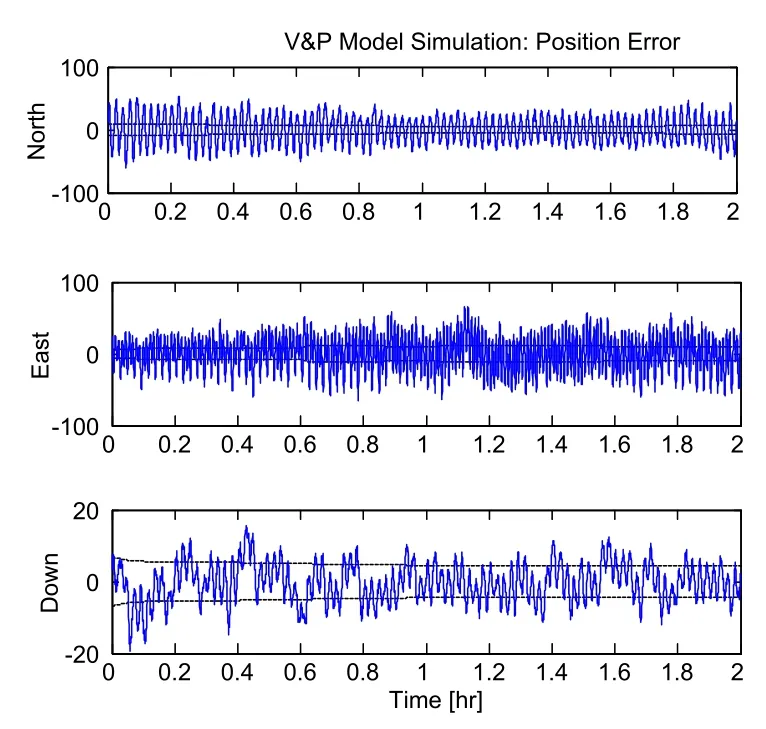
Figure 3:Position error of V&A model.

As shown by the simulation result,the tracking algorithm based on pseudo-linear Kalman filter can achieve high aircraft GPS tracking accuracy.The reason is that the pseudo-linear model internally built by the algorithm proposed herein has strong adaptability,able to track the state values of the maneuvering targets.Additionally,the V&P model and V&A model built herein are equipped with distinctive characteristics.V&P model,which shows some advantages in terms of velocity estimation,can control the velocity errors in three directions within 9.1m,while V&A model achieves higher accuracy in respect of position prediction,able to control the position errors in three directions within 17.2.

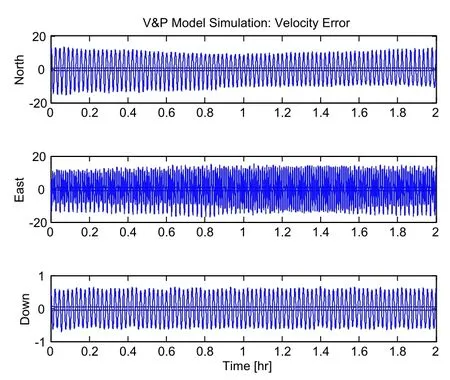
Figure 4:Velocity error of V&P model.

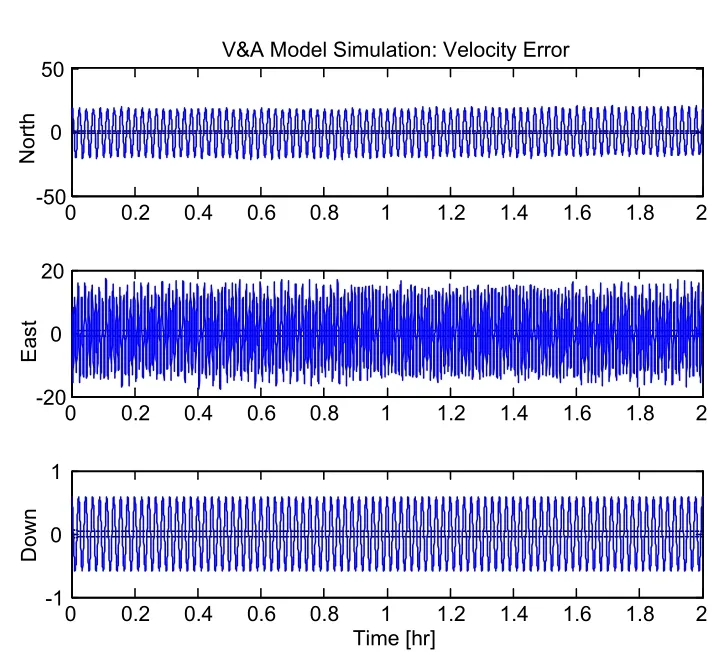
Figure 5:Velocity error of V&A model.

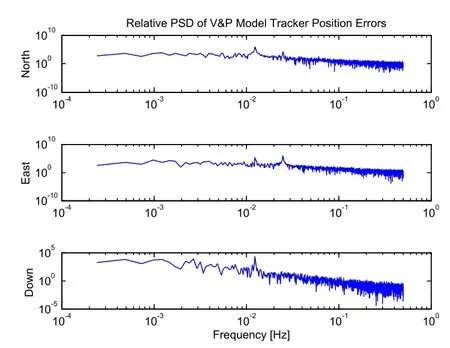
Figure 6:PSD of V&P model position error.

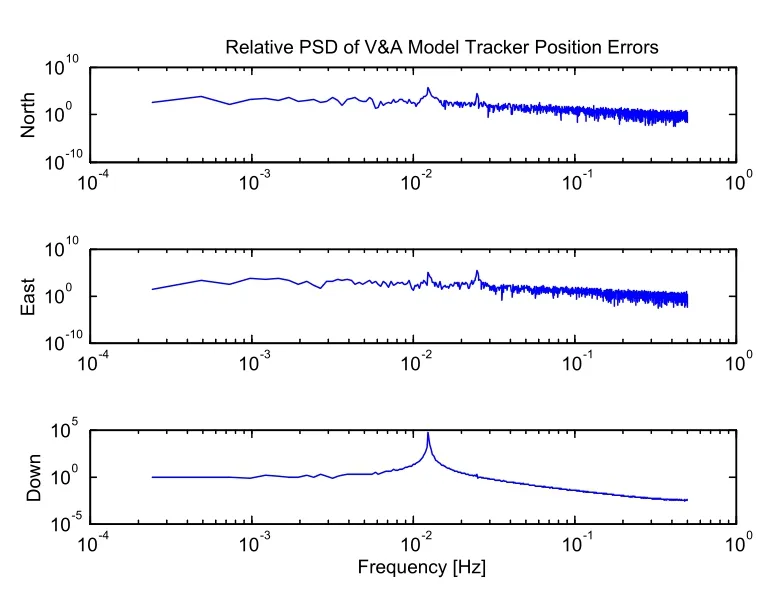
Figure 7:PSD of V&A model position error.

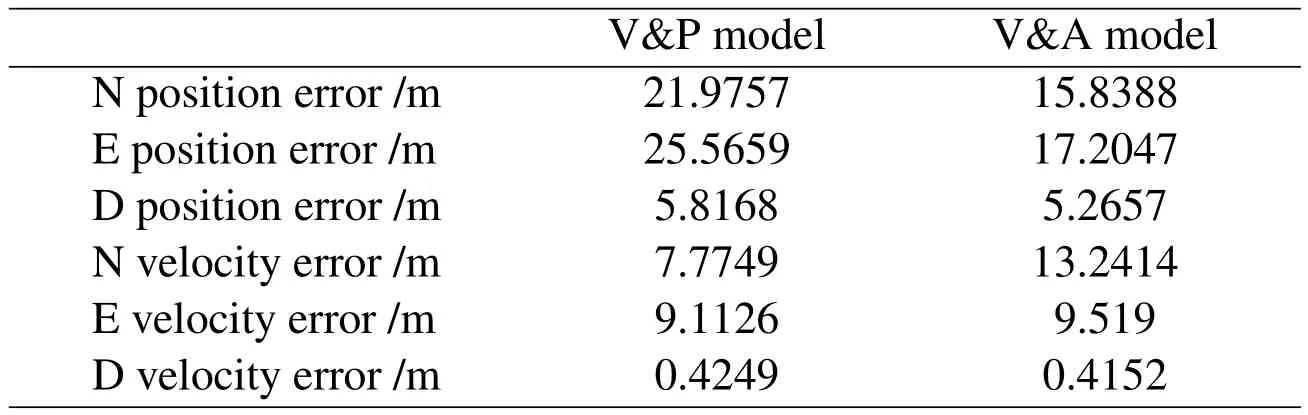
Table 1:Tracking average error in different model.

6 Conclusion

In view of active aircraft GPS tracking characteristics,the tracking algorithm based on pseudo-linear Kalman filter is hereby proposed to upgrade the target tracking efficiency.Meanwhile,by transforming the tracking algorithm,the pseudo-linear filter model is built to track the moving targets by way of traditional Kalman filter algorithm.Besides,the improved algorithm has been verified in different models.The experiment demonstrates that the tracking algorithm based on pseudo-linear Kalman filter can consist well with the characteristics of active aircraft GPS tracking,thus attaining high tracking accuracy and robustness.

Acknowledgement:This work is partially supported by the National Natural Science Foundation of China(61501521);National Natural Science Foundation of China(U1330133);National Natural Science Foundation of China(61473153);National Natural Science Foundation of China(61403421);National Natural Science Foundation of China(61203266);Defense Advanced Research Project of China(40405070102).Thanks for the help.

Mosavi,M.R.;Nabavi,H.;Nakhaei,A.(2014):Neural technologies for precise timing in electric power systems with a single–frequency GPS receiver.Wireless Personal Communications,vol.75,no.2,pp.925–941.

Teng,Y.L.;Shi,Y.B.(2012):Clock–based RAIM method and its application in GPS receiver positioning.Journal of Central South University of Technology,vol.19,no.6,pp.1558–1563.

Baiden,G.;Bissiri,Y.;Luoma,S.;Henrich,G.(2014):Mapping utility infrastructure via underground GPS positioning with autonomous telerobotics.Tunnelling and Underground Space Technology,vol.39,pp.6–14.

He,Y.H.;Martin,R.;Bilgic,A.(2014):Scalable low–complexity GPS and DGPS positioning using approximate QR decomposition.Signal Processing,vol.94,pp.445–455.

Nievinski,F.G.;Larson,K.M.(2014):Forward modeling of GPS multipath for near–surface reflectometry and positioning applications.GPS Solutions,vol.18,no.2,pp.309–322.

Zhou,Y.;Yang,X.;Mi,C.(2012):State estimation of unequipped vehicles utilizing microscopic traffic model and principle of particle filter,CMES:Computer Modeling in Engineering&Sciences,vol.89,no.6,pp.497–512.

Wang,H.K.;Haynes,R.;Huang,H.Z.;Dong,L.T.;Atluri,S.N.(2015):The use of high–performance fatigue mechanics and the extended kalman/particle filters,for diagnostics and prognostics of aircraft structures.CMES:Computer Modeling in Engineering&Sciences,vol.105,no.1,pp.1–24.

Rao,K.D.;Reddy,B.S.(1996):Ridge regression based EKF for GPS navigation under bad GDOP conditions.IETE Journal of Research,vol.42,no.6,pp.377–382.

Yazdanparast,M.;Vosooghi,B.(2014):A research on Damavand magma source model using GPS data.Geomatics,Natural Hazards and Risk,vol.5,no.1,pp.26–40.

Liu,Y.J.;Ding,F.(2011):Hierarchical least squares identification method for periodically non–uniformly sampled systems.Control and Decision,vol.26,no.3,pp.453–456.

Chen,Z.M.;Bo,Y.M.;Wu,P.L.;Zhou,W.J.(2013):A new particle filter based on organizational adjustment particle swarm optimization.Applied Mathematics&Information Science,vol.7,no.1,pp.179–186.

1China Satellite Maritime Tracking and Controlling Department,Jiangyin,214431,China)

2Corresponding author.