Improved Adaptive Particle Filter for Integrated Navigation System

Mengchu Tian,Yuming Bo,Zhimin Chen,Panlong Wu,Gaopeng Zhao

Improved Adaptive Particle Filter for Integrated Navigation System

Mengchu Tian1,Yuming Bo1,Zhimin Chen2,3,Panlong Wu1,Gaopeng Zhao1

Particle filter based on particle swarm optimization algorithm is not precise enough and easily trapping in local optimum,it is difficult to satisfy the requirement of advanced integrated navigation system.To solve these problems,an improved adaptive particle filter based on chaos particle swarm was proposed and used in GPS/INS integrated navigation system.This algorithm introduced chaos sequence to update the weight and threshold,which could improve the quality of samples and reduce the local optimization and enhance the global searching ability.In addition,the avoid factor was set which made the particles be away from low likelihood area.Finally,simulation results indicate that this algorithm improved the accuracy and robustness of GPS/INS integrated navigation system.

Adaptive;Particle filter;Integrated navigation;Chaos;Avoid factor.

1 Introduction

GPS/INS integrated navigation system has upgraded the overall performance of navigation system[Soon,Scheding,Lee,and Durrant-Whyte(2008)] significantly based on complementation between the advantages of GPS and those of INS in terms of error propagation.With GPS position information or velocity information used for periodic calibration by INS,the performance of integrated navigation will be superior to that of any sub-system applied independently [Bhatt,Aggarwal,and Devabhaktuni(2012)].Provided GPS receiver is capable of receiving the information sent by at least four satellites,GPS will be able to offer solution position information,and INS will measure the position and attitude information of the aircraft by means of angular rate sensor and linear acceleration.It is proved that integrated navigation can conquer respective deficiencies to deliver more accurate and reliable navigation information to carriers.

As the filtering algorithm used most frequently in the integration scheme,Kalman filtering can produce some positive filtering effects in the environment of linear model and Gaussian noise[Cho(2014)].Nevertheless,Kalman filtering will result in severe errors if the maneuvering amplitude of carriers is large or GPS signal is disturbed or shielded.It is found that particle filter can make up for the aforementioned deficiencies of Kalman filtering[Zhou,Yang,and Mi(2012)]and involve itself in filtering in the face of non-linear model and non-Gaussian noise.Despite so,particle filter cannot address the problem of particle shortage effectively,or ensure the accuracy without a large number of particles in unknown initial state[Chen,Bo,Wu,and Yu(2012);Wang,Haynes,Huang,Dong,and Atluri(2015)].PF based on Intelligent Optimization Algorithms conduces to significant improvement of particle degradation in PF and great enhancement of precision[Chen,Bo,Wu,and Zhou(2013)].Particle swarm optimization-based PF(PSO-PF)is a typical representative of Intelligent Optimization Algorithm which introduces PSO algorithm into PF[Yang and Sun(2013)].Through introduction of the latest measurement value to the sample distribution,along with the utilization of PF algorithm for sampling process optimization and constantly update of particle speed,the sample distribution is inclined to move to the area with higher posterior probability.PSO-PF improves the particle degradation of PF and is easier for actualization[Yang and Sun(2013)].Unfortunately PSO-PF is a process of iterative optimization which will prolong the calculation time because of the high iterative frequency,and thus is hard to meet the needs of real-time integrated navigation.Moreover,PSO-PF may be easily trapped into local optimization,influencing the precision and stability of target tracking.

In this paper,efforts are devoted to bringing forth a GPS/INS navigated integration system based on improved particle swarm optimization algorithm.In this system,chaos algorithm is introduced into particle swarm optimization algorithm to optimize the initialization and update process of weight and threshold value of particle filter algorithm,which has not only heightened the quality of initial samples and algorithm’s global searching ability,but also reduced local extrema.Meanwhile,escape factor is designed to keep the particles away from the areas of true values to some extent,which has contributed to a higher filtering accuracy.

2 Building of integrated navigation model

2.1 State and measurement equations

The application of filter to GPS/INS integrated navigation system is ultimately intended for a more accurate navigation parameter[Hu,Gao,and Zhong(2015)],and the selection of filter state normally resorts to indirect process,i.e.,the error ΔXof the navigation parameter outputted by a certain navigation system is taken as filter’s estimated state.While indirect process is used for estimation,the state of filter will be the combination of various errors in navigation system,without participating in the computing processes of the navigation parameters in navigation system,such as the computing process of INS’mechanical layout equation.Therefore,the estimation process of filter is independent of the computation of the navigation parameters in original navigation system,and the inertial navigation system(INS)can still have its strength of high update frequency fully revealed.

Supposing the combination mode of GPS/INS integrated navigation system relies on the combination between attitude and velocity,system’s measurement values can be divided into two values[Ding,Wang and Rizos(2007)],namely,difference value of position measurement and that of velocity measurement.Difference value of position measurement means that the difference between the position information(about longitude,latitude and altitude)rendered by INS and the information of relevant position calculated by GPS receiver is figured out as measurement information.Difference value of velocity measurement means that the difference between the information rendered by INS and the information of relevant velocity offered by GPS receiver is worked out as another type of measurement information.The error state equation of GPS/INS integrated navigation system is shown as follows:

The position measurement information of INS can be expressed as the sum of true value and corresponding error under the geographic coordinate system.

The position measurement information offered by GPS receiver can be expressed as the difference between true value and corresponding error under the geographic coordinate system.

Where λt,Lt,andhtstand for actual location,andNE,NN,andNUfor the errors of GPS receiver in the eastward,northward and skyward directions.

The position measurement vector is defined as follows:

Where,

The variances of measurement noise arerespectively.

Where,σpis the pseudo-range measurement error of GPS receiver.

The velocity measurement information of INS can be expressed as the sum of true value and corresponding velocity error under the geographic coordinate system.

WherevE,vN,andvUrepresent the true velocities along eastward,northward and skyward axes under geographic coordinate system.

The velocity measurement information of GPS can be also expressed as the difference between true value and corresponding velocity measurement error under the geographic coordinate system

WhereMN,ME,andMUconstitute the components of velocity measurement errors of GPS receiver along three axes,namely,northward,eastward and skyward axes.Below is the definition of velocity measurement vector:

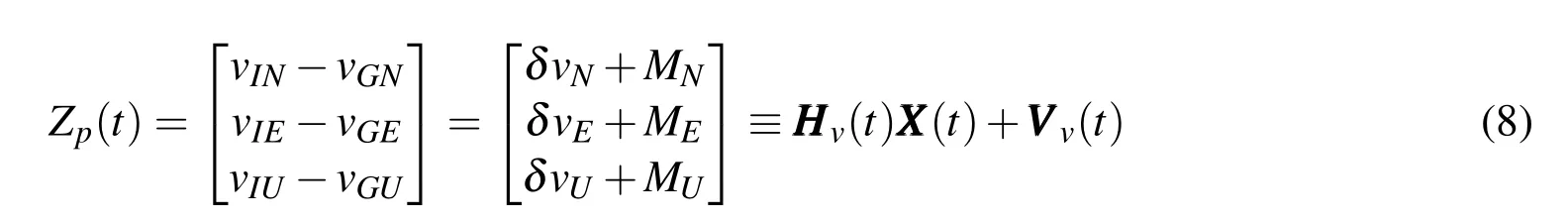
Assuming the measurement velocity of pseudo-range rateof GPS receiver is,the standard deviations of the eastward,northward and skyward velocity errors resulting from pseudo-range rate will be:

The combination of position measurement vector with velocity measurement velocity can figure out the measurement equation of GPS/INS position and speed integration system as follows:

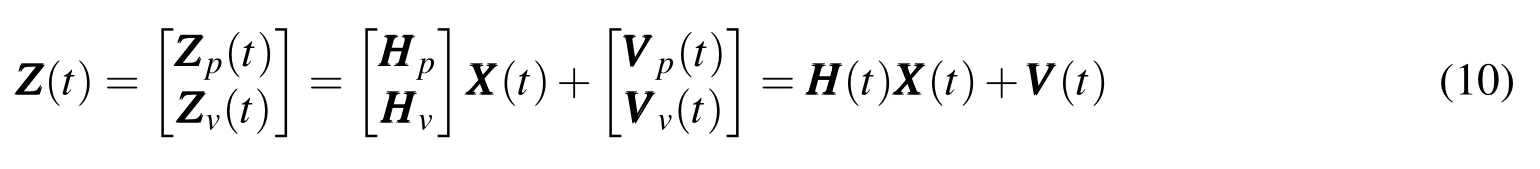
2.2 Discretization of state and measurement equations

Following result can be obtained through the discretization of state equation(1)and measurement equation(10):

Where,

As required by filter,the system and measurement noises of state and measurement equations should be equipped with following characteristics:

Where,

3 Particle filter

In the indirect estimation on the integrated navigation,navigation parameter error equation constitutes the main part of system’s state equation.However,considering that there is a small error,the rules of navigation parameter error can be described by the classical Kalman filtering and first-order linear approximation equation in case of the requirement for low accuracy,and its model error will not be high.

Particularly,however,the military field has made an increasingly higher demand on the accuracy of integrated navigation in recent years,because of which the model error resulting from the use of low-order approximation cannot be ignored any more.Meanwhile,given that the system noise and measurement noise may be the non-Gaussian noises,particle filter can be applied to non-linear system effectively in the environment of non-Gaussian noise effectively since conventional Kalman filtering is prone to divergence[Gordon,Salmond,and Smith(1993);Hwang and Sung(2013)].

Particle filter is an approximate calculation of Bayes estimation based on sampling theory.Combining Monte Carlo Method and Bayesian Theory together[Kong,Liu,and Wong(1994)],particle filter follows the basic thought that to find a group of random sample for approximation of posterior probability density,replace the in finitesimal calculus in light of posterior probability density function by sample mean value,and thus acquire the minimal estimate of variance[Li,Lu,and Gao(2010)].

Assuming the nonlinear dynamic process is expressed as follows:

If the initial probability density of the state is known asp(x0|y0)=p(x0),then the state predictive equation is:

and the state renewal equation is:

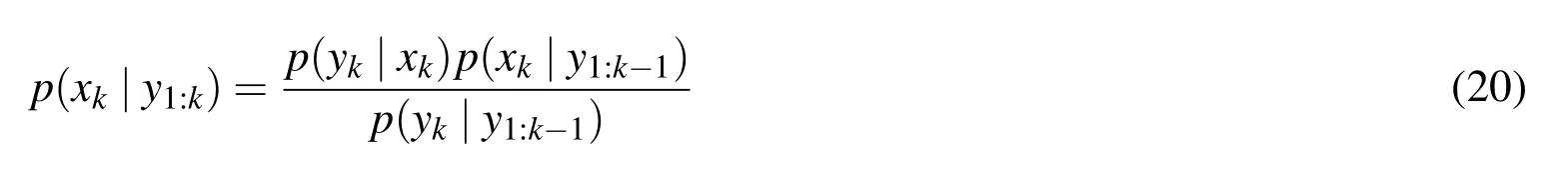
where

Supposing there is a known and easily-sampling importance functionq(x0:k|y1:k),which is rewrote as

Then the weight formula is

To sampleNsample pointsthen the probability density is:

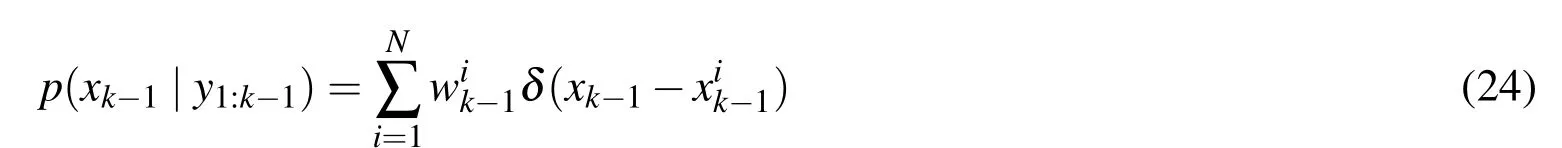
and the renewal probability density is:

State estimate:

4 PSO-PF algorithm

4.1 Basic PSO algorithm

Particle swarm algorithm is an intelligence optimization algorithm imitating birds’clustering movement.It is widely applied to target tracking,positioning and navigation,mode identification etc.by virtue of its advantages of simple concept,ease in actualization,fewer parameters,and effectiveness in solving complicated optimization and so on.PSO algorithm can be expressed as follows[Li,Bai,and Zhang(2010)]:to randomly initialize a particle swarm whose number ismand dimension isn,in which theith particle’s position isXi=(xi1,xi2,···xin)and its speed isVi=(vi1,vi2,···vin).During each iteration,the particles can renew their own speed and position through partial extremum and global extremum so as to reach optimization[MirHassani and Abolghasemi(2011)]. The update formula is:

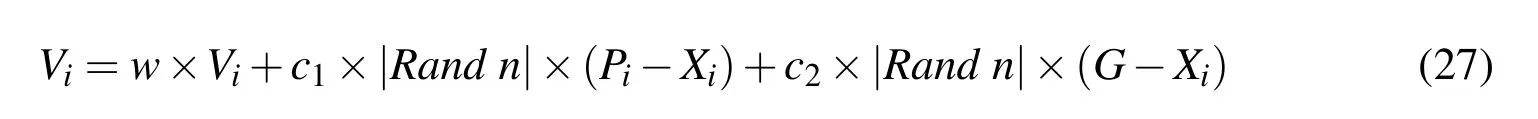
WhereRandis a random number within interval(0,1),wis the inertia coefficient(A larger inertia coefficient means stronger global search ability,while a smaller one stands for stronger local search ability),c1andc2are learning factors.

4.2 Description of standard PSO-PF algorithm

Though the particles with small weight make limited contributions to state estimation,they represent some information.The exclusion of particles will influence the accuracy of estimation.However,as PSO is introduced for sample optimization,particle set gets closer to high likelihood area prior.As a result of this,the distribution of particle weight will be more reasonable.The importance sampling process of conventional PF is suboptimal,whereas the incorporation of PSO algorithm will optimize the sampling process of PF,allow the weight of particle sets are more inclined to high likelihood region,accordingly solving the problem of particle impoverishment,and conducing to reduction of particle numbers required by PF.PSO method is fused with PF and the key lies in utilizing the optimal state valuePpbestexperienced by the particles and the state valuePgbestof the maximum particle with the greatest objective function value,and updating the speed and position of each particle on a real-time base through equation(29)and(30),accordingly forcing the particles to be closer to the real state.

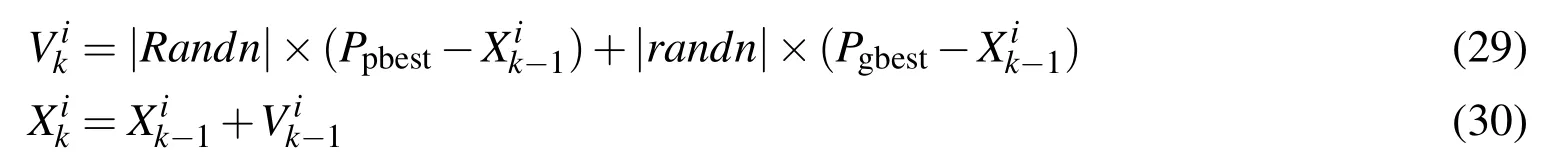
Wherewis the inertia coefficient,|Randn|and|randn|are positive Gaussian distribution random numbers.

5 Algorithms in this paper

5.1 Improvement principle

(1)In PSO-PF,initialization is a simple and random process,and it is not able to guarantee particles quality.To address this problem,this paper introduces chaos to PSO-PF to acquire CPSO-PF which can generate initial particles relying on the ergodicity of chaotic motion,cut down the probability of local optimum.

(2)As for PSO-PF,when it updates the speed and position of a particle by using equation(29)and(30),essentially it is to guide the next iteration position relying on its own information,individual extremum information and global information.In fact,this is a positive feedback process.When its own information and predominate,this algorithm may be easily trapped into local optimal solution.Focusing on the aforesaid problem,the algorithm presented in this paper attach the particles with chaotic motions,allowing the particles to jump out of the local extremum interval,and thus alleviating the phenomenon of local optimization.Finally the algorithm can find the optimal value within the global scope.

(3)As the improved algorithm has intensified the chaos perturbation against particle movement,the chaos perturbation will have partial particles approach the regions deviating from true values despite the improvement in the convenience of particle swarm and the reduction in local optimization.To address this problem,inspirations are brought from the characteristic that bacterial colonies draw close to the favorable growth environment and keep away from the adverse growth environment.On this basis,an escape factor is designed for the improved algorithm in the hope of keeping the particles away from the areas of true values for the sake of better particle quality.

(4)The non-linear setting of escape factor is required,since non-linear setting can not only reflect particle movement in a better way,but also ensure the rapid convergence of algorithm in early optimization stage.In the later stage,the particles will become better at deviating from the areas of true values,which can improve particle quality and avert the excessive perturbation of chaos algorithm.

5.2 Chaos

The basic thought of chaos optimization algorithm is to map the chaotic variable from chaotic space to solution space,and then make a search based on the ergodicity,randomness and regularity of chaotic variable.Chaos optimization algorithm is characterized by the insensitivity to initial value,easiness to get rid of local minimum,rapid search speed,high computation accuracy and global asymptotic convergence.

Chaos can be defined as a motion state with randomness[Wakano and Hauert(2011)]that can be generally acquired by Logistic mapping and Tent mapping etc.in this paper,the chaotic sequence is obtained through Logistic mapping and its iterative formula is[Zhu,Zhang,Wong,and Yu(2011)]:

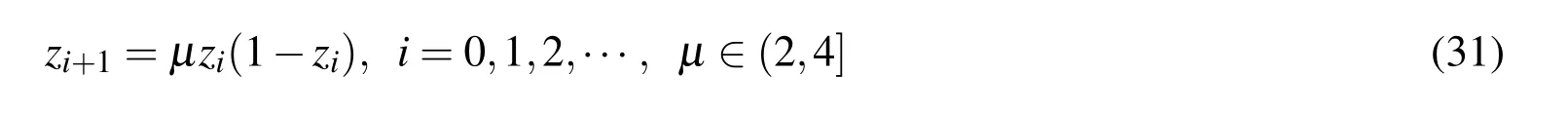
In which µ is the control parameter,whenµ=4,0≤z0≤1,Logistic is completely in a chaotic state and optimized searching can be conducted by using it.All the simulation in this paper is performed whenµ=4.

5.3 Escape Factor

Bacterial colonies usually live in different growth environments.For instance,in the laboratory with attractants and escape agent,individual bacteria will march toward the favorable growth environment but keep away from the adverse growth environment by instinct.This action will increase the survival probability of individual bacteria substantially and help bacteria find an environment more beneficial to growth in other places.

The improved algorithm proposed herein has recorded particle’s worst individual position and worst global location,withpwset as the worst individual position andgwas the worst global position:

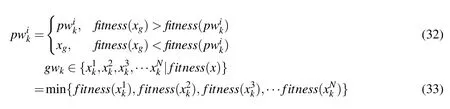
According to biological phenomenon of bacterial colonies,the attraction and escape behaviors are performed simultaneously.Thus,the particle velocity update of the algorithm proposed herein can be expressed as follows:

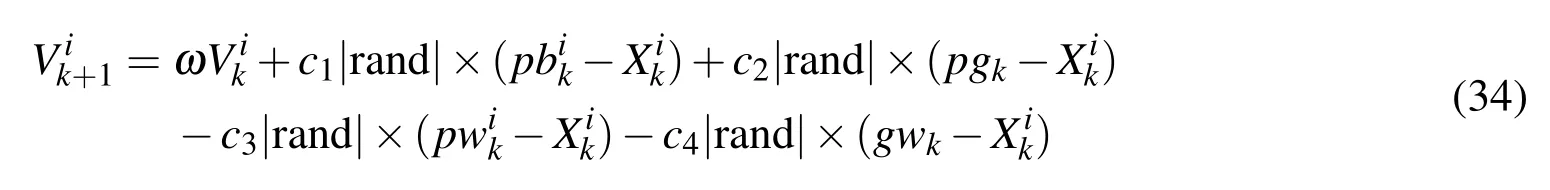
The intensity of particle’s convergence and escape behaviors is supposed to be controlled within a proper range.Otherwise,the chaotic particle movement will be easily incurred to affect the optimization result.In view of this,reference can be made to the method that sets the inertia weight of particle swarm optimization algorithm.Wherewis constant,it is set as 0.8.In this method,c3andc4are designed to change linearly over time,whereas the time series of linear changes cannot reflect the movement behaviors of particle swarm effectively,thus causing the increase in the number of iterations.Following numbers of experimental comparisons,the escape factorsc3andc4are set as follows:

In which iter max is the largest iteration number,and when iter max=150,the value curves ofc3andc4will be:

Figure 1:Iteration Diagram of Escape Factors.

The non-linear setting can assure the rapid convergence of the algorithm proposed herein in the early optimization stage,and in the later stage,the particles will become better at deviating from the areas of true values,which can improve particle quality and avert the excessive perturbation of chaos algorithm.

5.4 Steps for proposed algorithm improvement

The algorithm steps are listed as follows:

(a)Whenk=0,takeNparticles{,i=1,...,N}as samples from importance function at the initial time,and record its support interval[a0,b0].The importance density function[Li and Wang(2012)]is expressed in equation(36):

Giving the fitness function:

(b)Calculate the importance value

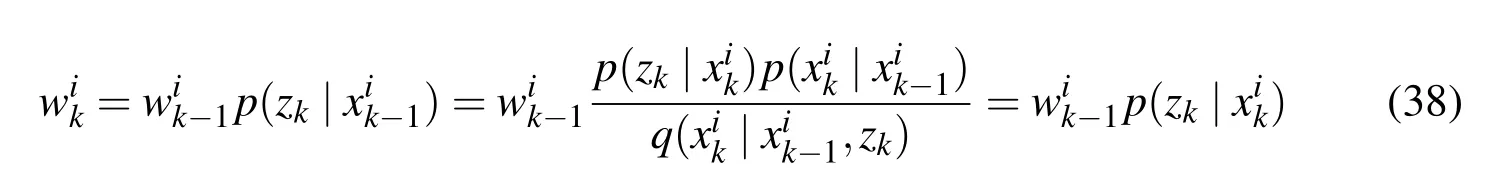
(c)The random numberz0within[0,1]will be generated.By using equation(31)for chaos calculation,a new N-dimensional vectorz={z1,z2,z3,···zN}is acquired and is mapped to the interval[a0,b0]of the sampling point of the importance function relying on equation(39).

In which°denotes the dot product among vectors.Then the initial samples ofNchaos assignments are obtained:

(d)To update the speed according to equation(34)and limit the speed withinvmax;maputo the range of chaotic motion[−β ,β ],and the disturbance quantity is:

Compare their fitness.IfYremains the same.

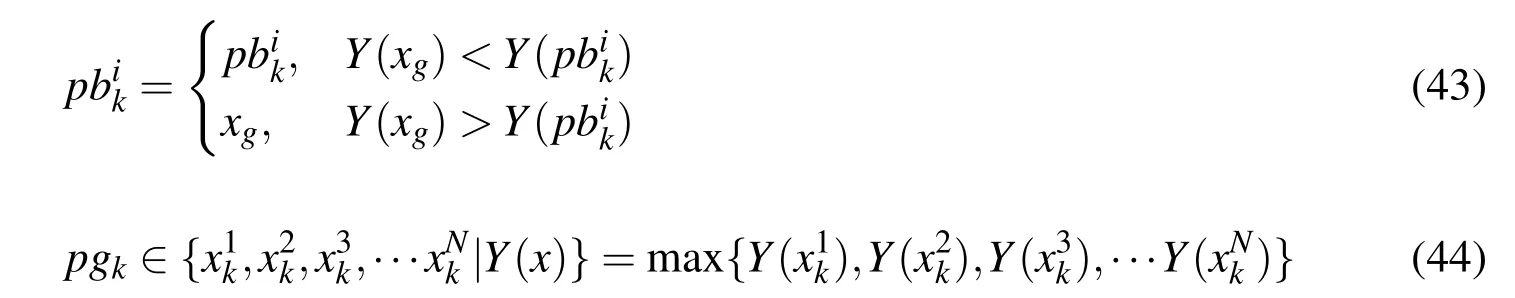
When the optimal value of particle complies with the initially-set threshold value ε,it is indicated that the particles have been already distributed around the true values.By now particle optimization should be stopped.

(e)Calculate the importance weight of the particles after optimization and perform normalization.

6 Experimental simulation

Let the latitude and longitude of the initial position of system state vector be 32°and 118°,respectively;the random and constant drift errors of the gyroscope be 0.05°/h,respectively;the random and constant bias errors of the gyroscope be 50µgand 100µg,respectively;the update cycle of inertial navigation be 0.01s;the cycle of Kalman filtering be 1s;and the simulation time be 500s.In this paper,an analysis is implemented on the position and velocity error curves along northward,eastward and skyward directions before and after the integrated filter correction.This aims to display the estimation results of the integrated filter more clearly,as well as present the trajectory charts of GPS and INS signals,error estimation curve,and the position and velocity error curve diagram along northward,eastward and skyward directions.

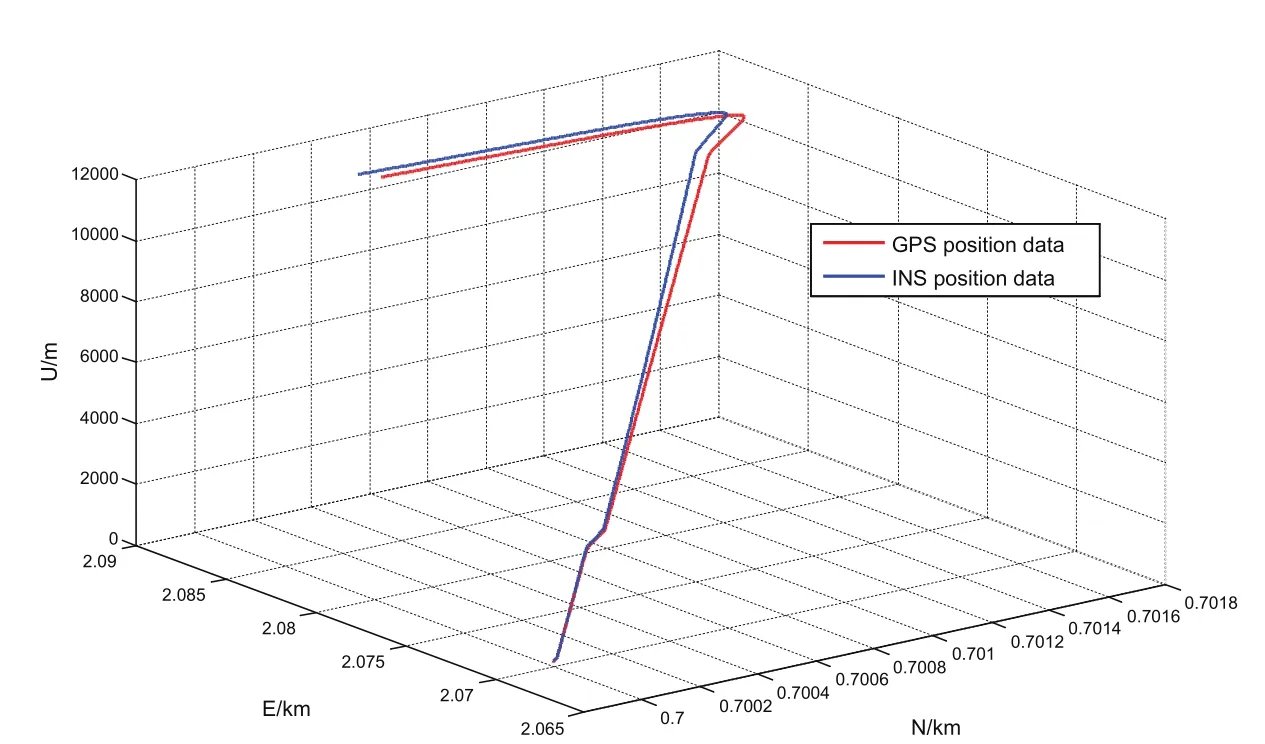
Figure 2:GPS/INS position data.

As shown by Figure 2,GPS locating signal varies slightly from INS locating signal in early stage,whereas their locating data are largely different from each other with the passage of time,which proves to be the unavoidable deficiency of INS locating.As revealed by Figure 3,the improved filtering algorithm has forecasted the noise errors and measurement deviation errors in an accurate way.As illustrated by Figures 4 and Figures 5,the system faces rapid divergence prior to the application of integrated filter,but the parameter errors of the system are correctly upon the use of improved particle filter algorithm.According to the figures above,integrated filter can control the position errors within 34m,with the mean square deviations of position errors along northward,eastward and skyward directions being 6.87m,7.2m,and 4.83m,respectively and those of velocity errors being 0.20m/s,0.21m/sand 0.14m/s,respectively.The statistical simulation result above has veri fied the feasibility of the improved particle filter algorithm proposed herein,and conquered the defect that filter is prone to failure on the condition of high observation accuracy to maintain a high estimation accuracy.

Figure 3:Noise prediction in different directions.

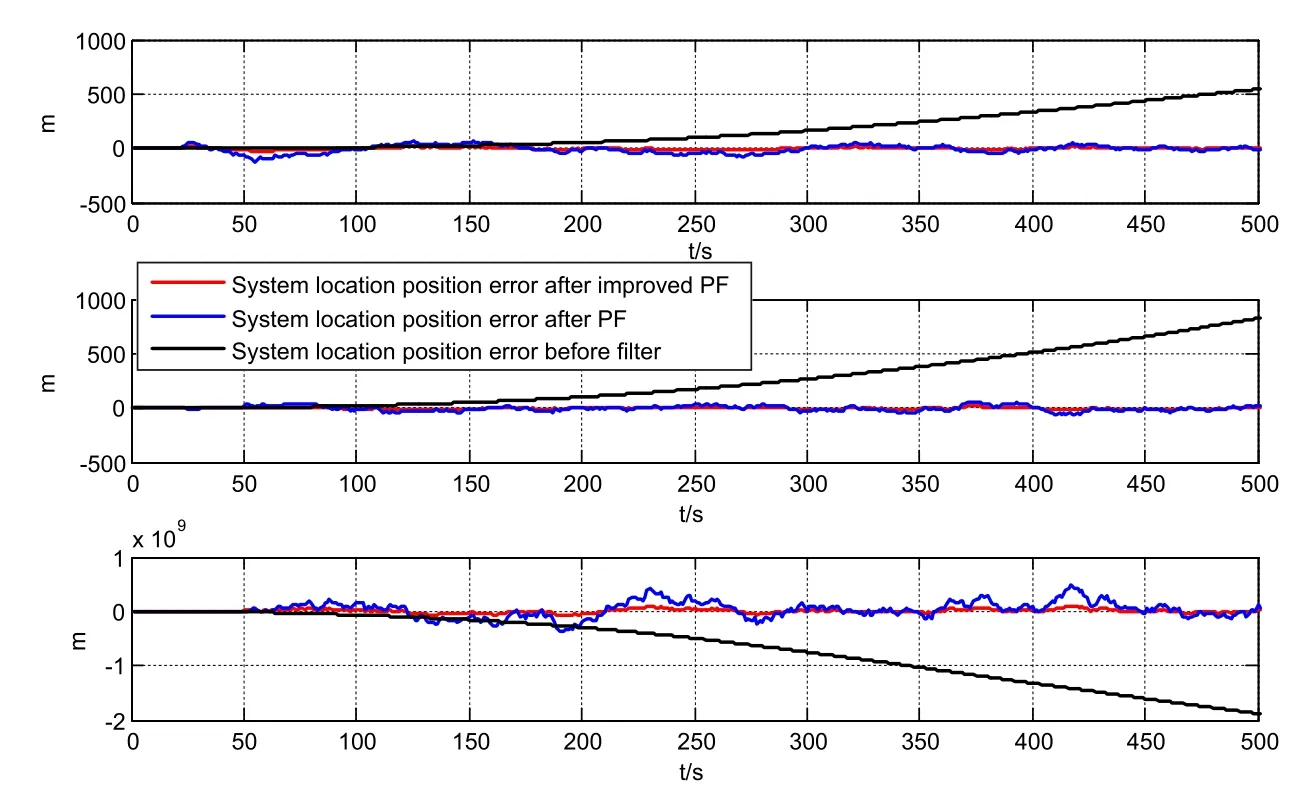
Figure 4:Position error in different directions.

Figure 5:Velocity error in different directions.

7 Conclusion

PSO-PF may be easily trapped in local optimization and not precise enough,thus is hard to reach the requirement of integrated navigation. After analyzing the deficiencies of PSO-PF,in this paper,an improved adaptive particle filter based on chaos particle swarm was proposed and used in GPS/INS integrated navigation system is presented.It increases the effectiveness of samples by using chaotic sequence for sample initialization and attaches chaotic perturbation to the state value in filtering,forcing the particles to be free from local optimization and reducing the iterations,and the avoid factor was set which made the particles be away from unreal area.The experimental data reveal that the algorithm proposed herein is applicable for GPS/INS integrated navigation system due to its high prevision.

Acknowledgement:This work is partially supported by the National Natural Science Foundation of China(61501521);National Natural Science Foundation of China(U1330133);National Natural Science Foundation of China(61473153);National Natural Science Foundation of China(61403421);National Natural Science Foundation of China(61203266);Defense Advanced Research Project of China(40405070102).Thanks for the help.

Soon,B.K.;Scheding,S.;Lee,H.K.;Durrant-Whyte,H.(2008):An approach to aid INS using time-differenced GPS carrier phase(TDCP)measurements.GPS Solution,vol.12,no.4,pp.261–271.

Bhatt,D.;Aggarwal,P.;Devabhaktuni,V.(2012):A novel hybrid fusion algorithm to bridge the period of GPS outages using low-cost INS.Expert Systems with Applications,vol.41,no.5,pp.2166–2173.

Cho,S.Y.(2014):IM- filter for INS/GPS-integrated navigation system containing low-cost gyros.IEEE Transactions on Aerospace and Electronic Systems,vol.50,no.4,pp.2619–2629.

Zhou,Y.;Yang,X.;Mi,C.(2012):State estimation of unequipped vehicles utilizing microscopic traffic model and principle of particle filter.CMES:Computer Modeling in Engineering&Sciences,vol.89,no.6,pp.497–512.

Chen,Z.M.;Bo,Y.M.;Wu,P.L.;Yu,S.L.(2012):A particle filter algorithm based on chaos particle swarm optimization and its application to radar target tracking.Journal of Computational Information Systems,vol.8,no.7,pp.3081–3090.

Wang,H.K.;Haynes,R.;Huang,H.Z.;Dong,L.T.;Atluri,S.N.(2015):The use of high-performance fatigue mechanics and the extended kalman/particle filters,for diagnostics and prognostics of aircraft structures.CMES:Computer Modeling in Engineering&Sciences,vol.105,no.1,pp.1–24.

Chen,Z.M.;Bo,Y.M.;Wu,P.L.;Zhou,W.J.(2013):A new particle filter based on organizational adjustment particle swarm optimization.Applied Mathematics&Information Science,vol.7,no.1,pp.179–186.

Yang,Z.;Sun,W.(2013):A set-based method for structural eigenvalue analysis using kriging model and pso algorithm.CMES:Computer Modeling in Engineering&Sciences,vol.92,no.2,pp.193–212.

Hu,G.;Gao,S.;Zhong,Y.(2015):A derivative UKF for tightly coupled INS/GPS integrated navigation.ISA Transactions,vol.56,pp.135–144.

Ding,W.;Wang,J.;Rizos,C.(2007):Improving adaptive Kalman estimation in GPS/INS integration.The Journal of Navigation,vol.60,no.3,pp.517–529.

Gordon,N.;Salmond,D.J.;Smith,A.F.M.(1993):Novel approach to nonlinear/non-Gaussian Bayesian state estimation.IEEE Proceedings F:Radar and Signal Processing,vol.140,no.2,pp.107–113.

Hwang,K.;Sung,W.(2013):Load balanced resampling for real-time particle filtering on graphics processing units.IEEE Transactions on Signal Process,vol.61,no.2,pp.411–419.

Kong,A.;Liu,J.S.;Wong,W.H.(1994):Sequential imputations and Bayesian missing data problems.Journal American Statistical Association,vol.89,no.425,pp.278–288.

Li,Y.Z.;Lu,Z.Y.;Gao,Q.X.(2010):Particle filter and mean shift tracking method based on multi-feature fusion.Journal of Electronics&Information Technology,vol.32,no.2,pp.411–415.

Li,Y.;Bai,B.;Zhang,Y.(2010):Improved particle swarm optimization algorithm for fuzzy multi-class SVM.Journal of Systems Engineering and Electronics,vol.21,no.3,pp.509–513.

MirHassani,S.A.;Abolghasemi,N.(2011):A particle swarm optimization algorithm for open vehicle routing problem.Expert Systems with Applications,vol.38,no.9,pp.11547–11551.

Wakano,J.Y.;Hauert,C.(2011):Pattern formation and chaos in spatial ecological public goodsgames.Journal of Theoretical Biology,vol.268,no.1,pp.30–38.

Zhu Z.L.;Zhang W.;Wong K.W.;Yu H.(2011):A chaos-based symmetric image encryption scheme using a bit-level permutation.Information Sciences,vol.181,no.6,pp.1171–1186.

Li,H.W.;Wang,J.(2012):Particle filter for manoeuvring target tracking via passive radar measurements with glint noise.IET Radar,Sonar&Navigation,vol.6,no.3,pp.180–189.

1School of Automation,Nanjing University of Science and Technology,Nanjing,210094,China

2China Satellite Maritime Tracking and Controlling Department,Jiangyin,214431,China)

3Corresponding author.