Analytical and FE Modeling of FG Beams Based on A Re fined Shear Deformable Beam Theory for Static and Dynamic Analyses of FG Beams With Thermoelastic Coupling

Cong Xie,Guangyu Shi,2

Analytical and FE Modeling of FG Beams Based on A Re fined Shear Deformable Beam Theory for Static and Dynamic Analyses of FG Beams With Thermoelastic Coupling

Cong Xie1,Guangyu Shi1,2

The static and dynamic thermoelastic analyses of the beams made of functionally graded materials(FGMs)are presented in this paper.Based on the refined third-order shear deformation beam theory proposed by the senior author and the variational principle,the governing equations of FG beams are deduced.The influence of temperature on Young’s modulus and coefficients of thermal expansion is taken into account when FG beams are subjected to thermal loading.The resulting governing equations are a system of the eighth-order differential equations in terms of displacement variables,and the thermoelastic coupling is included in the equations.An accurate and reliable two-noded beam element is developed for the bending and free vibration analysis of FG beams by employing the re fined third order shear deformation beam theory and the quasi-conforming element technique.Several typical examples of FG beams are solved using the present FG beam element to show the effects of the material distribution and thermal loading on the defections,stresses and natural frequencies of FG beams.The accuracy of both the analytical solutions and numerical results given by the proposed models are validated against the results reported in the literature or the 2D finite element results solved by the authors.The results show that the present models are capable of yielding not only accurate displacements but also accurate stresses and higher-order frequencies of free vibration for the FG beams with thermoelastic coupling.

Functionally graded(FG)beams,Modeling of FG beams,Thirdorder shear deformation beam theory,Thermoelastic coupling,FG beam element,Computational efficiency.

1 Introduction

Functionally graded materials(FGMs)are a special type of composite materials that material properties change smoothly and continuously from one surface to the other of a structural component by gradually varying the volume fraction of the constituent materials.Compared with traditional composite materials,FGMs possess various advantages,for instance,smooth transition of stress distributions,minimization or elimination of stress concentration,and can be designed to achieve specific properties for different applications etc.[Birman and Byrd(2007)].Thus micro/nano-beams,plates and membranes made of FGMs are widely used as structural or functional members in MEMS and NEMS[Ebrahimi and Salari(2015)].FGMs also have broad potential applications in modern engineering including aerospace,automobile,electronic, optic industries[Birman and Byrd(2007)].Structural components made of ceramic–metal FGMs are able to combine the advantages of ceramics and metals,and they are now developed as very useful and efficient structural members in high temperature environments.Consequently,the static and dynamic analyses of FGM structures are identified as an interesting and important field of study in recent years[Birman and Byrd(2007);Thai and Kim(2015)].

Many investigations on the thermoelastic analysis of FG beams are reported in the literature in the past two decades.Noda(1999)addressed the problem of thermal stresses in FGMs and studied the optimal composition pro files to decrease the thermal stresses in FGMs.Sankar and Tzeng(2002)presented an exact elasticity solution for thermal stresses of FG beams,in which the Young’s modulus and temperature field varies exponentially in the thickness direction.Chakraborty,Gopalakrishnan,and Reddy(2003)developed a beam element to study the thermoelastic behavior of FG beams,in which the beam element formulation was based on Timoshenko beam theory(TBT)and accounting for an exponential and a power law variation of the material properties of FG beam.Lü,Chen,Xu,and Lim(2008)developed semi-analytical elasticity solutions for the bending and thermal deformation of 2D FG beams with various boundary conditions,exponential variation of material properties were adopted in it.Giunta,Crisafulli,Belouettar,and Carrera(2013)presented a thermoelastic analysis of FG beams where the beam models are hierarchically derived by means of a unified formulation that makes the formulation independent from the displacements polynomial approximation order over the cross-section.Most of them considered thermal loadings,but the studies of FG beams accounting for the temperature-dependent characteristics of FGMs are rather limited.Mahi,Adda Bedia,Tounsi,and Mechab(2010)presented an analytical method for thermoelastic vibration analysis of symmetric FG beam subjected to initial thermal stresses with general boundary conditions.Zhang(2013)used the physical neutral surface and a high order shear deformation theory for the nonlinear bending analysis of FG beams in thermal environments.Shen and Wang(2014)investigated the nonlinear analysis of shear deformable FG beams resting on elastic foundations in thermal environments.

The accuracy of the resulting stresses is more important than the accuracy of resulting displacements in the real applications of shear deformable FG beams,thus it is important to develop FG beam models that are capable of accurately calculating the stresses of FG beams.By using the mixed-collocation with over-integration,Dong,El-Gizawy,Juhany,and Atluri(2014a)developed a 4-node quadrilateral membrane element for the analysis of homogeneous,FG or laminated thick-section beams.Later,they extended the 4-node membrane element to an 8-node solid element for the analysis of FG or laminated thick-section plates and shells[Dong,El-Gizawy,Juhany,and Atluri(2014b)].The numerical results show that the over-integration along beam thickness or plate thickness is a good scheme to accurately compute the stresses.The aforementioned 4-node quadrilateral plane element was also extended to the analysis of smart composite beams[Ray,Dong,and Atluri(2015)].The 2D 4-node element and 3D 8-node element developed by Dong,El-Gizawy,Juhany,and Atluri(2014a,2014b)with over-integration can yield accurate axial stress and transverse shear stress.However they are not computational efficient as the over integration used in the evaluations of element stiffness matrix and stresses demands more computations.By employing a more rigorous kinematics of displacements,Shi and Voyiadjis(2011)proposed a re fined third-order shear deformation beam theory.Wang and Shi(2012)demonstrated that this new beam theory is capable of yielding accurate transverse stresses and predicting correct boundary layer solutions at the locations with displacement boundary conditions.Wattanasakulpong,Gangadhara,and Kelly(2010)employed the aforementioned beam theory to investigate thermal buckling and thermoelastic vibration of FG beams under uniform temperature field,and they demonstrated that this re fined third-order shear deformation beam theory possess some significant features in comparison with Euler–Bernoulli beam theory and Timoshenko beam theory in particular for the high shearflexible FG beams.Zhang,He,Liu,Gan,and Shen(2014)used the beam theory proposed by Shi and Voyiadjis(2011)and a strain gradient elasticity theory to develop an analytical model for static and dynamic analyses of size-dependent FG microbeam resting on elastic foundations.And their results showed that the beam theory proposed by Shi and Voyiadjis is very accurate.Nevertheless,the modeling of FG beams based on this beam theory for bending analysis of FG beams with thermoelastic coupling is not found in the open literature.

The issue of computational efficiency of FG beam elements is also desirable in the real engineering application.Shi and Voyiadjis(1991)demonstrated that the assumed strain method which is based on the quasi-conforming element technique[Tang,Chen,and Liu(1980)]is an approach to formulate accurate and efficient shear flexible arch/beam elements and shell elements,since the resulting elements are not only free from shear locking,but also free from the time consuming numerical integration.The objectives of this paper are two-folded.The first objective is to use the re fined third-order shear beam theory proposed by Shi and Voyiadjis(2011)for the theoretical modeling of FG beams with thermoelastic coupling.The other is to present a reliable,accurate and efficient two-noded FG beam element for the bending and free vibration analyses of FG beams with thermoelastic coupling,in which the beam element is formulated based on the re fined third-order shear deformation beam theory and the quasi-conforming element technique[Tang,Chen,and Liu(1980);Shi,Lam,and Tay(1998)].The accuracy of both the analytical solutions and the numerical results given by the proposed models is validated by the comparison of the present results with the results reported in the literature or the 2D finite element results solved by the authors.The results show that the present models are capable of yielding not only accurate displacements but also accurate stresses and higher-order frequencies of free vibration for the FG beams with thermoelastic coupling.

2 Effective material properties of FGMs

A typical simply-supported FG beam composed of ceramic and metal is depicted in Fig.1,where the dimensions of the beam are of lengthL,thicknesshand widthb.It is assumed that the composition of a FG beam is varied from the top surface of the beam to its bottom surface,i.e.,the top surface(z=h/2)of the beam is ceramic-rich whereas the bottom surface(z=-h/2)is metal-rich,wherezis in the coordinate along the upward normal of the beam middle surface.

Figure 1:Schematic of a typical simply-supported FG beam

The volume fraction of ceramic,Vc,of the FG beam follows the Voigt model defined by a simple power law as

whereNis the volume fraction index and takes only positive values(0≤N＜∞).Then the effective material propertiesPf,such as Young’s modulusEfand coef ficient of thermal expansion αf,can be characterized by

in whichPcandPmrepresent the material properties of ceramic and metal respectively;Vmis the metal volume fraction and it satisfies the relationship ofVc+Vm=1.

From Eqs.(1)and(2),one has

Since FG structures are most commonly used in high temperature environment where significant changes in mechanical properties of the constituent materials are to be expected,it is essential to take account of the temperature-dependency of material properties for the accurate prediction of the mechanical response.Therefore,the effective Young’s modulusEfand coefficient of thermal expansion αfof FG beams are assumed to be temperature-dependent.They can be expressed as the following nonlinear function of temperature[Touloukian(1967)]

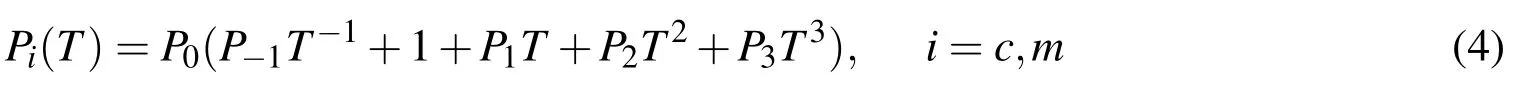
whereP0,P-1,P1,P2andP3are the coefficients of temperatureT(K)which are unique to the constituent materials.Since the mass density ρfdepends weakly on temperature change,it is assumed in this study that ρfis a function ofzonly.The effective material properties of selected Si3N4/SUS304 FGM are listed in Table 1[Reddy and Chin(1998)].A constant value of Poisson ratio is used for Si3N4/SUS304 FGM because there is only a small difference between the Poisson ratios of ceramic and metal and the influence of the manor change of Poisson ratio on the structural response is negligible.The average value ν=0.28 can be used for Si3N4/SUS304 FGM[Wattanasakulpong,Gangadhara,and Kelly(2010)].

The temperature field is assumed to be linearly distributed through the beam thickness when the FG beam is subjected to steady-state thermal loading,that is

The linear variation of temperature across FG beam thickness is justified when the thickness of a FG beam is within the dimension of milimeter.Substituting Eq.(5)into Eq.(4),the variation of FGM material properties through the beam thickness can be determined.

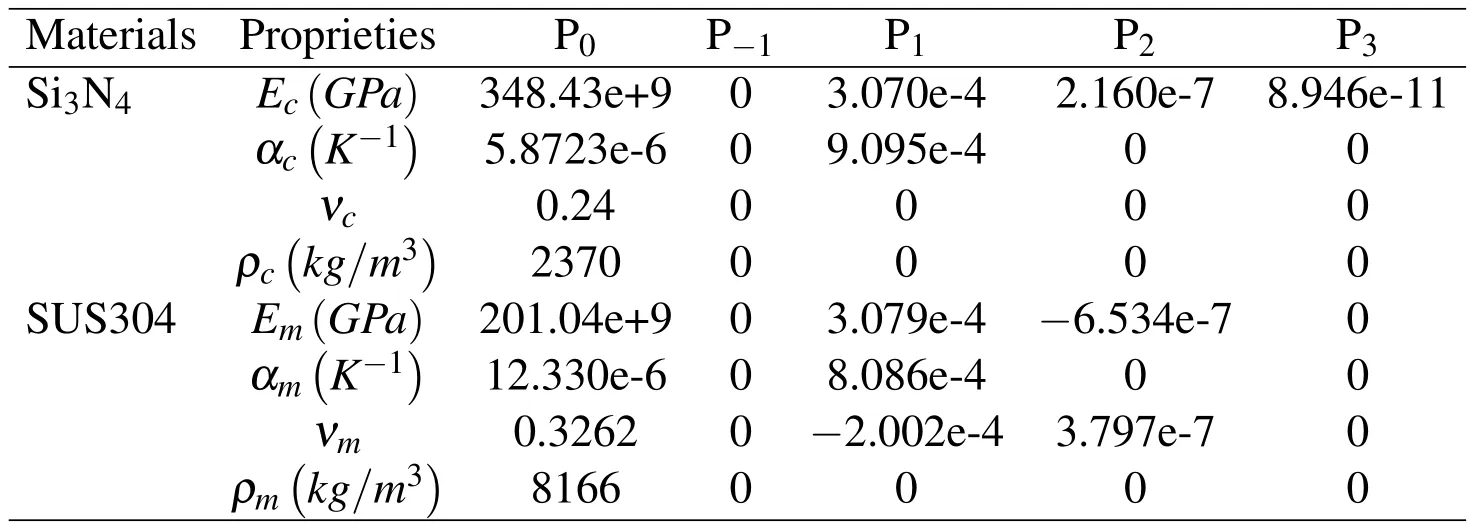
Table 1:Coefficients in temperature-dependent functions for ceramic and metals

3 Analytical modeling of FG beams

3.1 Kinematics of the re fined shear deformable beam theory and the corresponding trains

The displacement field in the re fined third-order shear deformation beam theory proposed by Shi and Voyiadjis(2011)is of the form

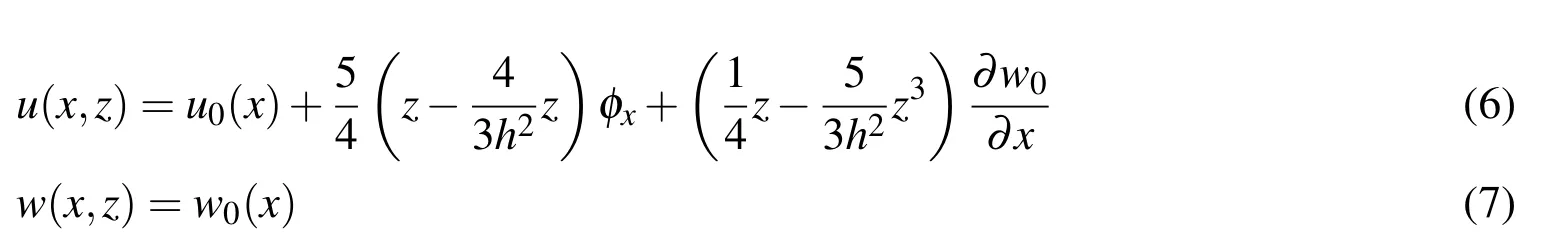
in which the quantities with subscript“0”denote the values at the middle surface of the beam wherez=0;u0andw0are the axial displacement and the deflection of a point on the beam reference plane respectively;φxis the averaged rotation of the beam cross-section through the beam thickness.

It follows from Eqs.(6)and(7)that the nonzero linear strains of a beam take the form

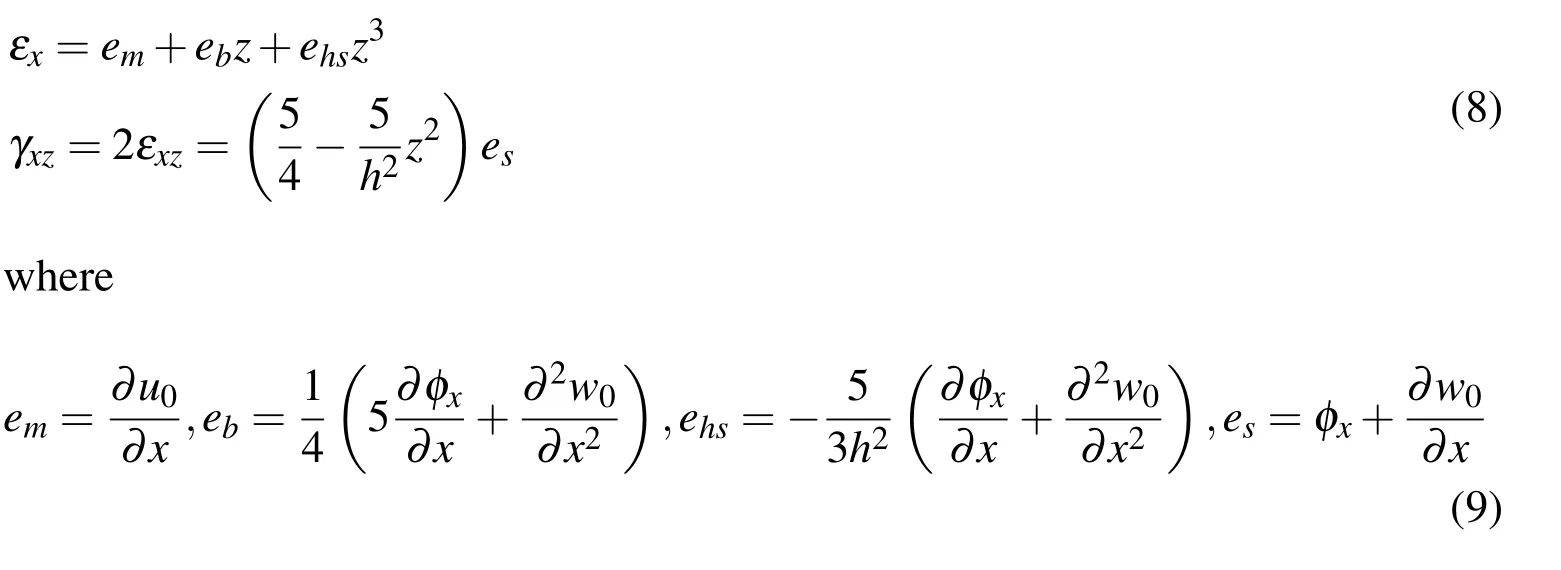
3.2 Constitutive relations of FG beams

Under the bending in thex-zplane induced by thermal-mechanical coupling loading,the constitutive relations of shear flexible FG beams made of isotropic material are of the form

in which

where ΔT(z)=T(z)-T0is the temperature rise from the reference temperatureT0at which there are no thermal strains.

3.3 Variational consistent equilibrium equations and the corresponding boundary conditions

It follows from Eqs.(8–10)that the strain energy of a FG beam with a lengthLand an area of cross sectionAcan be defined in terms of the generalized displacements u0,w0and φxas

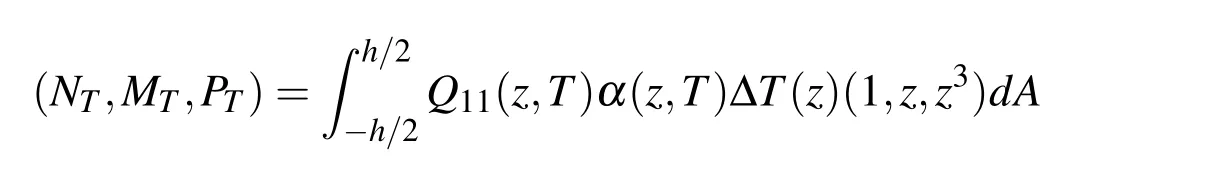
The various coefficients in the above expression are:A11is the extensional stiffness,B11is bending–extension coupling stiffness,D11is bending stiffness,E11is warping–extension coupling stiffness,F11is warping–bending coupling stiffness,H11is warping–higher order bending coupling stiffness,S11is shear stiffness;andNT,MT,PTare,respectively,the axial forces,bending moments and supplementary bending moment induced by thermal loading.

When the distributed bending moment is not considered,the external work of a beam performed by the distributed loadq(x)per unit length acting on the beam surface is of the form

Consequently,for a transverse shear deformable beam with the external load defined above,the corresponding variational principle leads to

By substituting Eqs.(12)and(14)into Eq.(15),using integration by parts and collecting the terms corresponding to δu0,δ φxand δw0in the line integral,one obtains the following three differential equations:

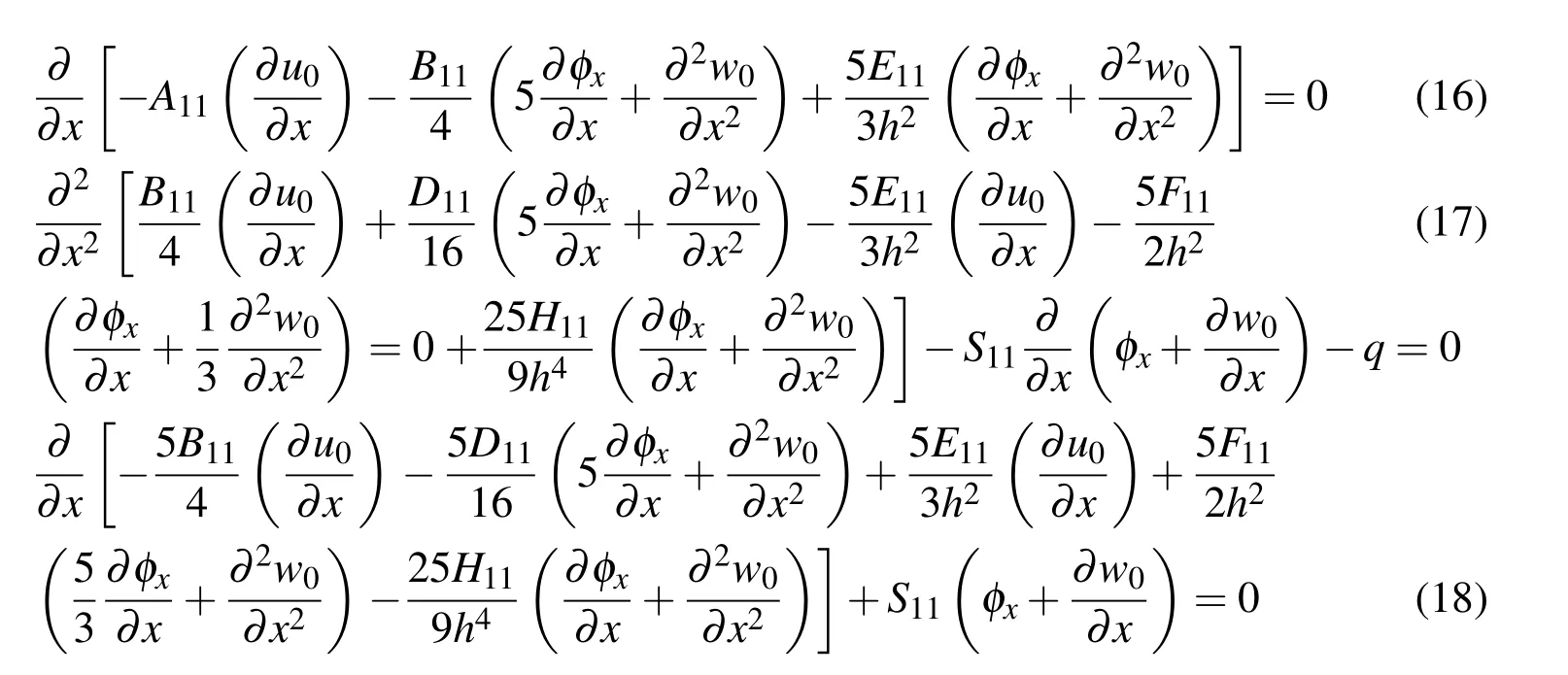
Denoting the generalized axial force corresponding to axial displacementu0as,the generalized bending moment acting on the beam cross section corresponding to φxas,the generalized transverse force corresponding to deflectionw0asand the supplementary bending moment corresponding to ∂w/∂xas,these quantities take the form

Utilizing the generalized stress resultants and stress couples defined in Eqs.(19–22),the boundary conditions at the typical supports of transverse shear deformable beams take the following form.

1.At a clamped support,

2.At the end with displacement free but with specified stresses,

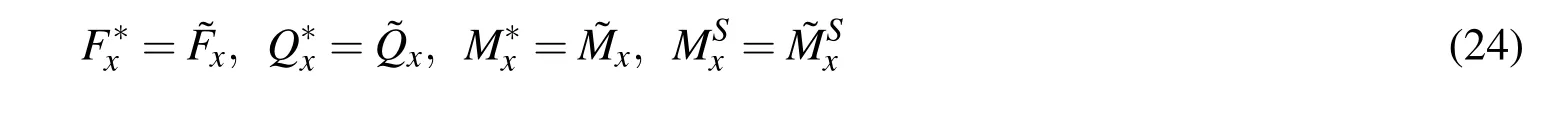
3.At a pin support,

4.At a roller support,

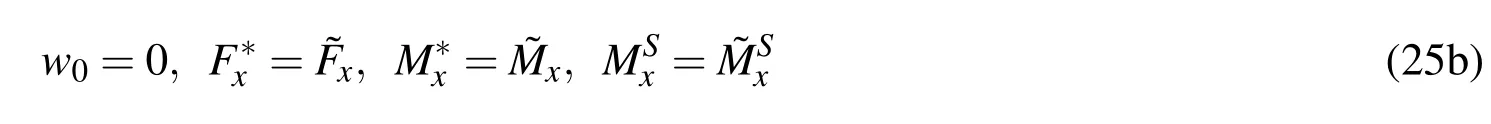
The quantities with“～”in the above expressions denote the values given by the specified stresses acting on the cross-section of beam end.The boundary conditions of a simply supported beam are of the combination of Eqs.(25a and 25b).It should be noted that under the action of thermal loading,the response of a simple beam supported by the pin support at its both ends is different from that a simple beam supported by a pin support at one end and by a roller support at the other.

4 Two-noded beam element of FG beams

The present formulation of FG beam element is based on the re fined third-order shear deformation beam theory proposed by Shi and Voyiadjis(2011),which has been proved a high accuracy and efficiency in both static and dynamic analyses[Wang and Shi(2013)].

4.1 Strains of shear deformable FG beams

By using a shear variable γ defined as[Shi,Lam,and Tay(1998)]

then Eq.(6)can be rewritten as

with α =1/4 and β =5/(3h2).

It follows from Eq.(27)and Eq.(7)that the new expressions of the axial strain and the transverse shear strain under consideration take the forms

in which

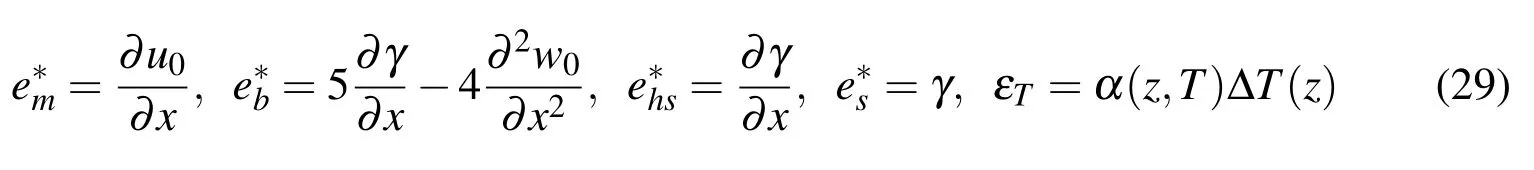
The strains defined above are the functions of the deflection and transverse shear deformation,and they results in aC1-continuity element under the displacement based formulation.Corresponding to the strains defined in Eq.(29),the simplest nodal degrees of freedom at nodei,qi,for a two-noded beam element can be chosen as

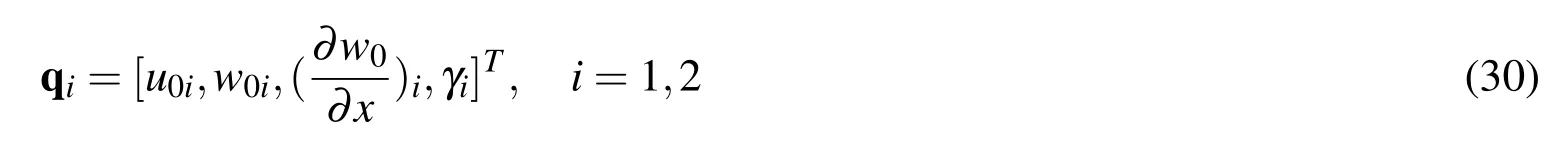
Fig.2 illustrates the two-noded FG beam element in this study.The nodal variables in Eq.(30)lead to a cubic approximation for deflectionw0and a linear transverse approximation for shear strain γ.Then it follows from second expression of Eq.(29)that the resulting bending strain of the beam element is linear.Because the bending strain is the dominant term in bending problems,then in finite element analysis,the strain expressions derived from the displacement defined in Eq.(27)should lead to a more accurate result than those higher-order beam theories in which the bending strain is merely approximated as a constant over an element,even though these beam elements have the same number of degrees of freedom at each node[Shi,Lam,and Tay(1998)].

Figure 2:The nodal variables of the present two-noded element of shear flexible FG beams

4.2 Element stiffness matrix of shear flexible FG beam

Now let consider a FG beam element of lengthland rectangular cross-section with thicknesshand widthb.The strain energy of the beam element with the strains defined in Eqs.(28)and(29),Πe,is of the form

The stiffness parameters in Eq.(31)are defined in Eq.(13).The element strains in Eq.(31)can be expressed in terms of the element nodal displacement qeand the element strain matrices as follows

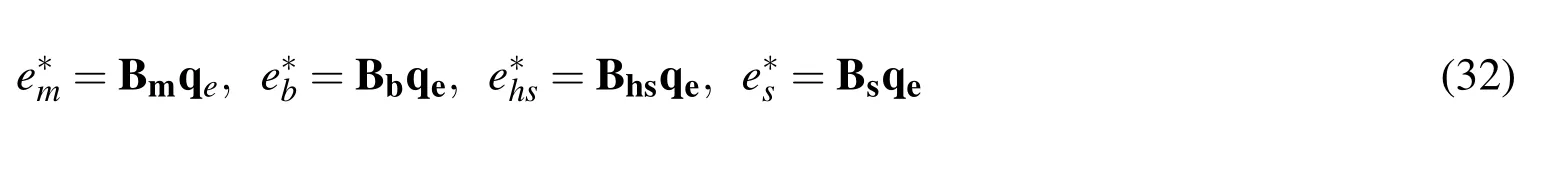
Consequently,the element strain energy Πein Eq.(31)takes the form

If one de fines element membrane,bending,shear gradient,transverse shear and coupling stiffness matrix,respectively,as the following

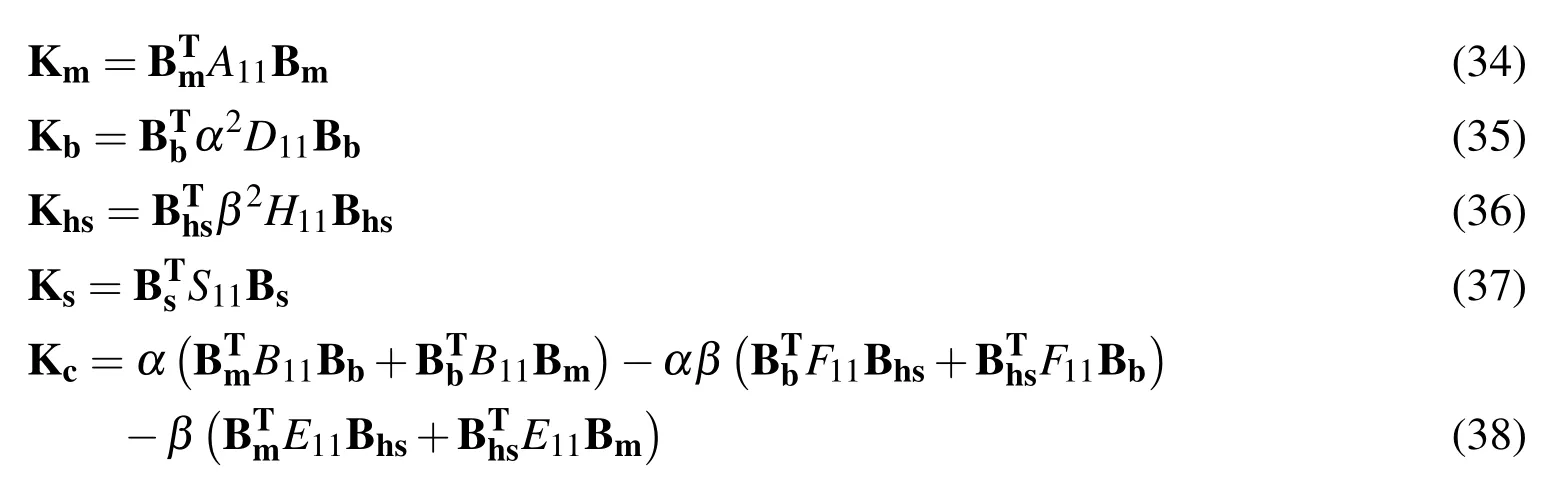
then the element stiffness matrix K obtained from Eq.(33)is of the form

The thermal loading vector PTis of the form

4.3 Element strain matrix evaluated by the quasi-conforming element technique

The quasi-conforming element technique[Tang,Chen,and Liu(1980)]is employed in this work to evaluate the element strain matrices in Eq.(32).The element strain field in a quasi-conforming element is interpolated directly over the element domain rather than differentiated from the assumed displacement field,and the compatibility in an element domain is satisfied in a weak form.Let aprimesignify the assumed element strain field,then the element strain energy in Eq.(31)can be modified as

whereαm,αbi(i=1,2),αhsandαsare the strain parameters of the assumed element field which can be determined from the weak form of compatibility given in Eq.(41)at the element level.

Let the integrals for the weak form of strain compatibility in Eq.(41)be satisfied individually,and let the test functions in Eq.(41)be the same as the trial functions.Then the last four integrals in Eq.(41)lead to the strain matrices defined in Eq.(32)as

By substituting B matrices above into Eqs.(34–38),the element stiffness matrix can be obtained.Since the B matrices given in Eqs.(43–46)are either constant or involved with linear function,the resulting element stiffness matrix can be evaluated explicitly,i.e.no numerical integration is needed,which makes the resulting beam element very computationally efficient.

5 The FE modeling for dynamic analysis of FG beams

5.1 Velocities of shear deformable beams

It follows from the Eq.(27)and Eq.(7)that the velocities in thex-direction andz-direction respectively take the forms

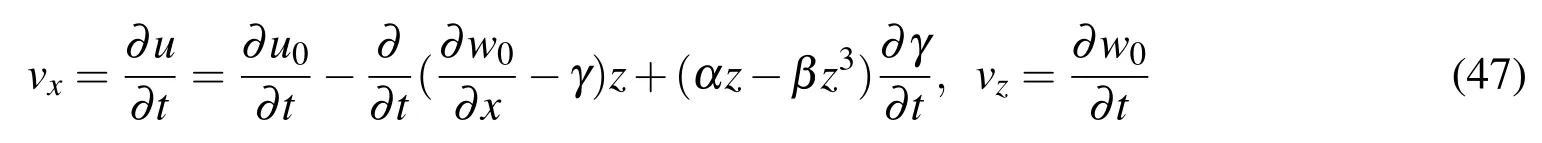
5.2 Equations of motion of FG beam element

In dynamic analysis,the equation of motion is expressed in terms of the element stiffness matrix and the mass matrix obtained from Hamiltonian principle.Let ΠeandTebe the element strain energy and kinetic energy respectively,then Hamiltonian principle states that

In the analysis of natural frequency of a system,the work done by external forces is neglected and the damping is not considered. Then Eq.(48)leads to the equilibrium equations of a system as

The mass matrix based on the shear deformation beam theory will be presented in next section.

5.3 Consistent mass matrix of shear deformable beams

The kinetic energy of a FG beam element with density ρ(z),Te,corresponding to the re fined shear deformable beam theory used in this work takes the form

By defining

the element kinetic energyTecan be written as

The expression above shows that similar to the stretching and bending coupling in the stiffness matrix,there is also an axial and rotary velocity coupling in the mass matrix when the density is not symmetric about the reference plane of the FG beams.The coupling of the transverse shear velocity and the deflection slope velocity is always non-zero as long as the transverse shear deformation is not zero.The element displacement interpolations are needed to evaluate the velocities defined in Eq.(47).The displacements over the beam element depicted in Fig.2 can be interpolated in terms of the element nodal displacement vector qeas

Mw,Muand Mwxis,respectively,the usual transverse,axial and rotary inertia matrices;Mγis the mass matrix resulting from the higher-order displacement;and Muw,Muγand Mwxγare the coupling terms of different components of the axial displacement.The variational consistent mass matrix defined above can account for the contribution of the higher-order displacement to the mass matrix and the results show that the consistent mass matrix can provide more accurate results than those given by lump mass matrix.

6 Examples of static analysis of FG beams

Analytical and numerical analyses based on the governing equations and the FG beam element given in the previous sections are carried out to evaluate static deflections and stresses of FG beams.The effects of the material distribution and thermal loading on the defections and stresses of various FG beams are studied by the numerical results given by the present FG beam element,and the validation against other results is carried out to show the accuracy and efficiency of the present FG beam element.

6.1 Convergence and accuracy study of the present FG beam element

A clamped-clamped FG beam with aspect ratio ofL/h=15and subjected to a point loadFat the midspan is considered here.The beam is made of Si3N4/SUS304 with volume fraction indexN=1000(metal rich).Table 2 shows the convergence of the deflection given by the present FG beam element,in which the deflections of FG beam are normalized as:

The non-dimensional deflections obtained from different beam elements and the analytical solution given by the present governing equations are tabulated in the table.It can be seen from the results in the table that the present FG element is more accurate than FGM-HSDT-RN and HSDT-FGM-SR presented by Kadoli,Akhtar,and Ganesan(2008),particularly when a coarse mesh is used.

6.2 Deflections of FG beams under mechanical loading

The influence of the volume fraction index on the deflections of FG beams is shown by the bending analysis of simply-supported FG beams under action of uniformly distributed lateral load.The width of the beam is 0.1m and different aspect ratios ofL/hare considered.The FG beam is composed of Aluminum(Al:Em=70 GPa,

νm=0.3)and Zirconia(ZrO2:Ec=200 GPa,νc=0.3).The top surface of thebeam is metal-rich whereas the bottom surface is ceramic-rich[¸Sim¸sek(2009)](it should be noted that the volume fraction of ceramicVcin the present example is defined differently from that defined in Eq.(1)).The defections of the FG beam are normalized by the static deflection of the fully aluminum beam under the uniformly distributed load,¯w=w/(5ql4/384EAlIz).

Table 2:Calculated deflections of clamped FG beam with L/h=15 and loaded at the midspan

The maximum non-dimensional deflections of the FG beams with different values of volume fraction indexes and aspect rations are listed in Table 3,where HOSDT stands for the higher-order shear deformation theory[¸Sim¸sek(2009)]and BSWI stands for the B-spline wavelet on the interval finite element method[Zuo,Yang,Chen,Xie,Zhang,and Liu(2014)].The use of the B-spline wavelet can achieve very accurate approximation for the field variables of one-dimensional beam problems with the price of higher cost of computation.20 elements are used in the present FEA to take account of the distributed load.Table 4 shows that the present results agree well with the results reported by¸Sim¸sek(2009)and Zuo,Yang,Chen,Xie,Zhang,and Liu(2014),which demonstrates that the present FG beam element is very accurate.

6.3 Axial stresses of modulus graded plate under uniaxial loading

The structures with FGMs behave differently from the structures made of conventional materials.Thus it is interesting and worthwhile to examine the axial stress distribution of a structural member with graded modulus under the action of simple tensile loading.To this end,a cantilevered plate with modulus grading subjected to a uniformly distributed tensile load at the free edge is considered.As shown in Fig.3,the non-dimensional width,length and thickness of the plate are 10,10,and 1 respectively[Dong,El-Gizawy,Juhany, and Atluri(2014b)].Non-dimensional Young’s modulus of the plate is exponentially varying in the thickness directionzwhereE=eβzwith β =log5.ThusE=1 at the lower surface andE=5 at the upper surface of the plate.Poisson ratiov=0 in this numerical example.

The cantilevered plate shown in Fig.3 can be directly modeled as a cantileveredbeam with a width of 10 since the Poisson ratiov=0 in this plate.The axial stress atx=5,y=0 of the cantilevered plate with the graded modulus is computed by one element of the present FG beam element.The distribution of the resulting axial stress across the plate thickness is displayed in Fig.4,and the 3D element results obtained from the CEH8 C0brick element given by Dong,El-Gizawy,Juhany,and Atluri(2014b)and the analytical solution given by Zhong and Yu

(2007)are also given in the figure.It should be noted that vertical axiszin Fig.4 denotes the plate thickness coordinate which is different from the coordinate system used by Dong,El-Gizawy,Juhany,and Atluri(2014b).The analytical solution of Zhong and Yu(2007)was considered as the exact solution in the paper of Dong,El-Gizawy,Juhany,and Atluri(2014b).It should be pointed out that the present stress results are deduced directly from the constitutive relations described in the previous section.It can be seen from Fig.4 that the axial stress prediction given by the present FG beam element for this modulus graded plate coincides with the exact solution even with a coarse mesh composed of only one beam element,which demonstrates that the present FG element are very computational efficient and accurate in the stress prediction.

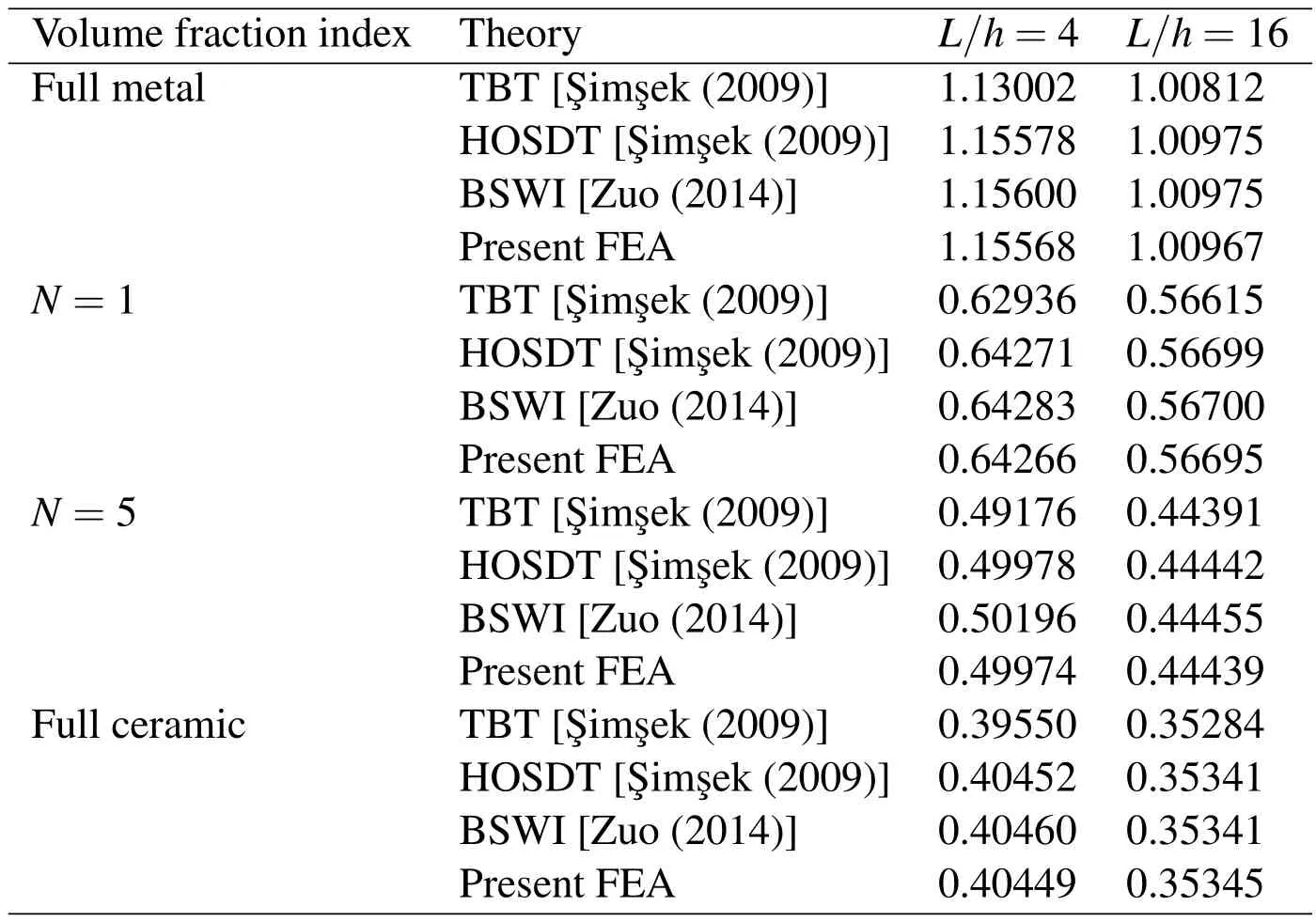
Table 3:Maximum non-dimensional deflections of FG beams with various values of volume fraction indexes and different aspect ratios

Figure 3:A cantilevered modulus graded plate subjected to a tensile load

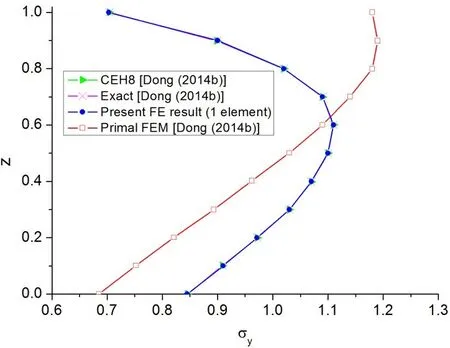
Figure 4:Axial stress distribution across the plate thickness at x=5,y=0 for a cantilevered modulus graded plate under uniformly distributed tensile load(N=1/length)at the free end.

6.4 Stresses of modulus graded beam under transverse force

A cantilevered beam with modulus grading subjected to a unit transverse force at the free end is considered in this example.As illustrated in Fig.5,the nondimensional length and thickness of the beam are 5 and 1 respectively[Dong,El-Gizawy,Juhany,and Atluri(2014a)].Non-dimensional Young’s modulus is exponentially varying in the beam thickness direction,i.e.E=eβzwith β =log5.ThusE=1 at the bottom surface of the beam,andE=5 at its top surface.Poisson ratiov=0 in this numerical example.

Figure 5:A cantilevered beam with graded modulus subjected to a transverse force

The axial stress of the cantilevered beam atx=0.5 and the transverse shear stress atx=2.5 are computed by the present FG beam element.The distributions of the axial stress and transverse shear stress across the cantilevered FG beam thickness are plotted in Fig.6 and Fig.7 respectively,where the 2D membrane element results obtained from the mixed-collocation element(CEQ4)developed by Dong,El-Gizawy,Juhany,and Atluri(2014a)and the analytical solution given by Zhong and Yu(2007)are also displayed in the figures for comparison.Fig.6 shows that the neutral axis of this modulus graded beam is shifted toward the top surface because of the higher value of Young’s modulus at the top surface.One can also find it from Fig.6 that the present FG beam element yields very accurate axial stress prediction for this modulus graded beam even with a coarse mesh composed of only three beam elements,which demonstrates that the present two-noded FG element possesses not only highly computational efficiency but also high accuracy.

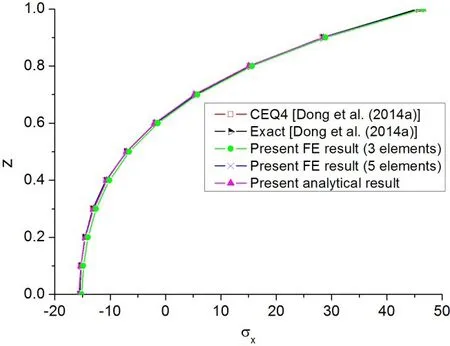
Figure 6:Axial stress distribution across the thickness of the cantilevered modulus graded beam(x=0.5)under a unit transverse force at the free end

The present shear stresses shown in Fig.7 agree well with the exact solution,but they are not as accurate as the present results of the axial stress.This can be at-tributed to that the shear deformable beam theory proposed by Shi and Voyiadjis(2011)was originally presented for the analysis of shear flexible beams made of homogeneous materials,in which the shear function is symmetric with respect to the beam middle surface.As a result the symmetric shear function would result in some error when it is applied to the computation of transverse shear stress of a modulus graded beam that is a beam made of inhomogeneous material.Nevertheless,the present shear stress results are satisfactory in general as shown in Fig.7,and the shift of the maximum shear stress can also be characterized correctly in the present result,which indicates that the re fined shear deformation beam theory proposed by Shi and Voyiadjis(2011)can be efficiently applied to the modeling of modulus graded beams.

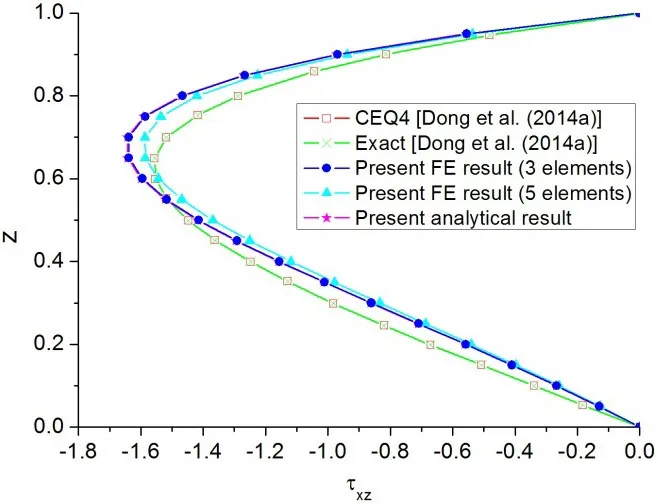
Figure 7:Shear stress distribution across the thickness of the cantilevered modulus graded beam under a unit transverse force at the free end

6.5 Defections and stresses of FG beams under thermal loadings

Since FG structures are most commonly used in high temperature environments,it is essential to take thermal loadings into consideration for the accurate validation of any new model of FGMs.A Si3N4/SUS304 FG beam supported by a pin and a roller,respectively,at each end of the beam is considered for the study.The aspect ratio of the beam is ofL/h=20 andb=h[Shen and Wang(2014)].20 beam elements are used in the present FEA.Table 4 shows the maximum non-dimensional deflections(wmax/h)of Si3N4/SUS304 FG beams under the non-uniform thermal loading ofTt=500 K,Tb=300 K for different values of the volume fraction indexes.The present results are validated by the comparison with 2D FEM results obtained from the commercial code ANSYS by the authors.In the 2D finite ele-ment model of ANSYS,the gradations of Young’s modulus,coefficient of thermal expansion and the temperature field across the beam thickness are modeled by an equivalent multilayered FG beam in which each lamina is assumed to be homogeneous and equal thickness.Two lamination schemes of 40 laminae and 80 laminae respectively along the FG beam thickness are used in the equivalent layered FG beam models based on ANSYS to ensure the convergence of the numerical results given by the equivalent multilayered FG beam.Each lamina in the equivalent multilayered beam model of the FG beam is meshed by two layers of Plane183 elements,and 800 elements are used in the beam axial direction.It can be seen from Table 4 that the deflections given by the present FG beam element agree very well with the numerical results obtained from the 2D plane stress elements of ANSYS.

Table 4:Maximum non-dimensional defections of FG beams with different N under thermal loading

The distributions of the calculated axial stresses through the cross-section of the midspan of Si3N4/SUS304 FG beams induced by the thermal loading for the case of volume fraction indexN=2 are plotted in Fig.8.It can be seen from Fig.8 that the ANSYS 2D results of the equivalent multilayered beam are approaching to the present FE results with the increase of the lamina number used for the equivalent multilayered beam,which demonstrates the accuracy of the present stresses results.

The influence of non-uniform thermal loading on the maximum non-dimensional deflections of Si3N4/SUS304 FG beams is depicted in Fig.9,where different volume fraction indexes are considered.Fig.10 illustrates the axial stress distributions cross the FG beam thickness at the midspan of the Si3N4/SUS304 FG beams withN=2 under different non-uniform thermal loadings.

The stress in a FG beam subjected to thermal loading also depends on the distribution of its constituents. The influence of the volume fraction index of Si3N4/SUS304 FG beams on the axial stress induced by non-uniform thermal loading is illustrated in Fig.11,whereTt=500 K,Tb=300 K.It can be observed from Fig.11 that the shift of the neutral surface of the FG beams gets larger as the increase of the volume fraction indexN.

The accuracy of the predicted stress of the FG beam elements under thermo-mechanical coupling loading is practically interested and important in the engineering applica-tion of FG beam.Fig.12 shows the axial stress distributions of Si3N4/SUS304 FG beams withN=2 under different thermo-mechanical coupling loadings.

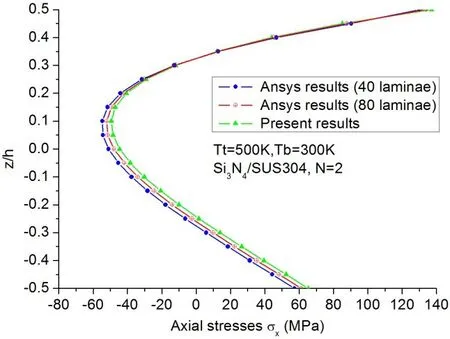
Figure 8:Axial stress distribution across the cross-section(at x=L/2)of Si3N4/SUS304 FG beam with N=2 under non-uniform thermal loading of Tt=500 K and Tb=300 K

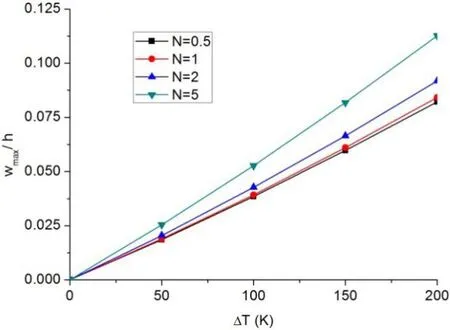
Figure 9:Maximum non-dimensional deflections of FG beams versus non-uniform temperature rise for different values of volume fraction index

7 Examples of free vibration analysis of FG beams

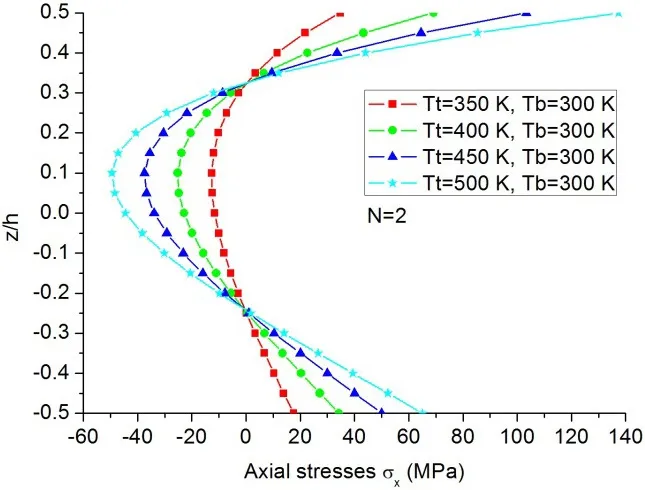
Figure 10:Axial stress distributions of FG beams with N=2 under various nonuniform thermal loadings

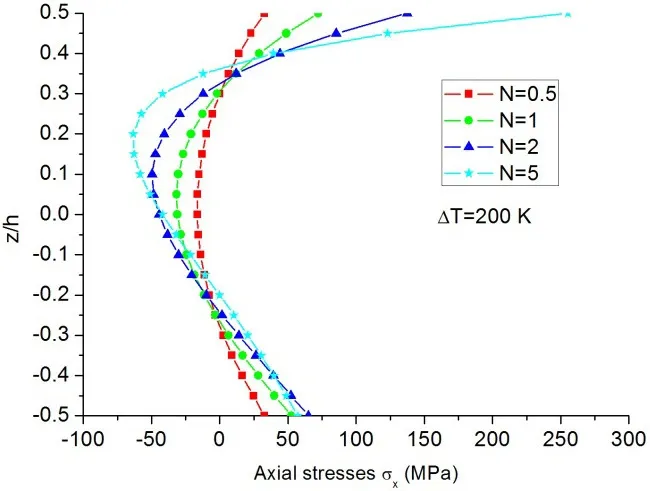
Figure 11:Axial stress distributions(at x=L/2)of the FG beams with different values of volume fraction index under non-uniform thermal loading of Tt=500 K and Tb=300 K

Numerical analyses based on the FG beam element given in the previous sections are carried out to study the free vibration of FG beams.The effects of the material distribution and thermal loading on the frequencies of various FG beams are studied by the numerical results given by the present FG beam element,and the validation against other results are carried out to show the accuracy and efficiency of the present FG beam element.

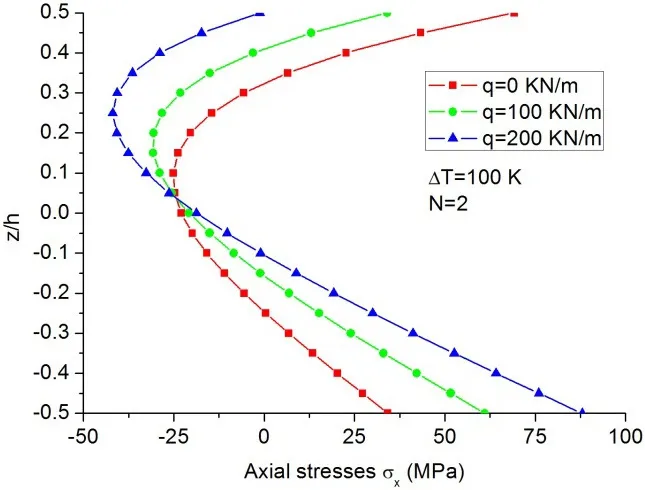
Figure 12:Axial stress distributions(at x=L/2)of the FG beams with N=2 under uniformly distributed load and non-uniform thermal loading of Tt=400 K and Tb=300 K

7.1 Natural frequencies of FG beams

To verify the free vibration results given by the present FG beam element,some numerical examples are solved for the FG beams without thermal loadings.The simply supported FG beam under consideration is composed of ceramic(Ec=380 GPa,νc=0.3)and aluminum(Em=70 GPa,νm=0.3),and the aspect ratio of the beam isL/h=20.Constant density is assumed for FG beam with ρ=2700 kg/m3[Aydogdu(2007)].The non-dimensional frequency is defined asIn order to accurately calculate the higher-mode frequencies of FG beam,40 elements are used in the present FEA.The non-dimensional fundamental frequencies given by different theories are tabulated in Table 5,and the non-dimensional frequencies of the fifth-mode given by different theories are listed in Table 6.In these two tables,CBT denotes Euler-Bernoulli beam theory,FSDBT stands for Timoshenko beam theory,PSDBT stands for the parabolic shear deformation beam theory and ESDBT stands for the exponential shear deformation beam theory[Aydogdu and Taskin(2007)].

The results in Table 5 indicate that the fundamental frequencies given by different theories are almost identical.However,the differences of the frequencies of the fifth-mode given by different theories are quite considerable.CBT,in which the transverse shear deformation is not taken into account,yields a much higher frequency of the fifth-mode flexural vibration.The rest of the beam theories give quite close prediction for the frequency of the fifth-mode,while the present FG beam element which is based on the re fined third-order beam theory proposed by Shi andVoyiadjis(2011)gives a higher value.It was shown by Wang and Shi(2013)that the present re fined third-order shear beam theory yields almost the identical results of the fundamental frequency with other higher-order beam theories,but yields more accurate higher-mode frequencies than other higher-order shear deformation beam theories.The accuracy of the higher-mode frequencies given by the present FE modeling will be validated in next subsection by the comparison with the numerical results obtained from the 2D element of ANSYS with very fine mesh.

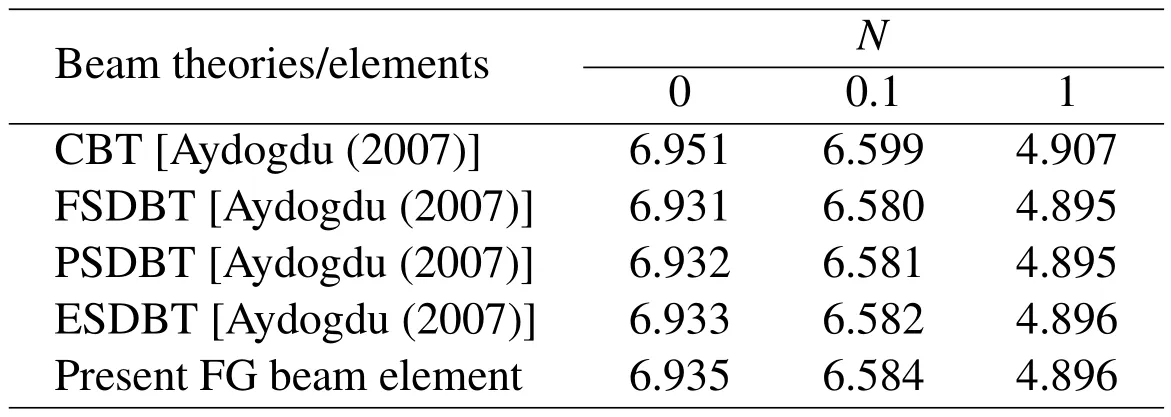
Table 5:Non-dimensional fundamental frequencies of simply supported FG beam given by different theories

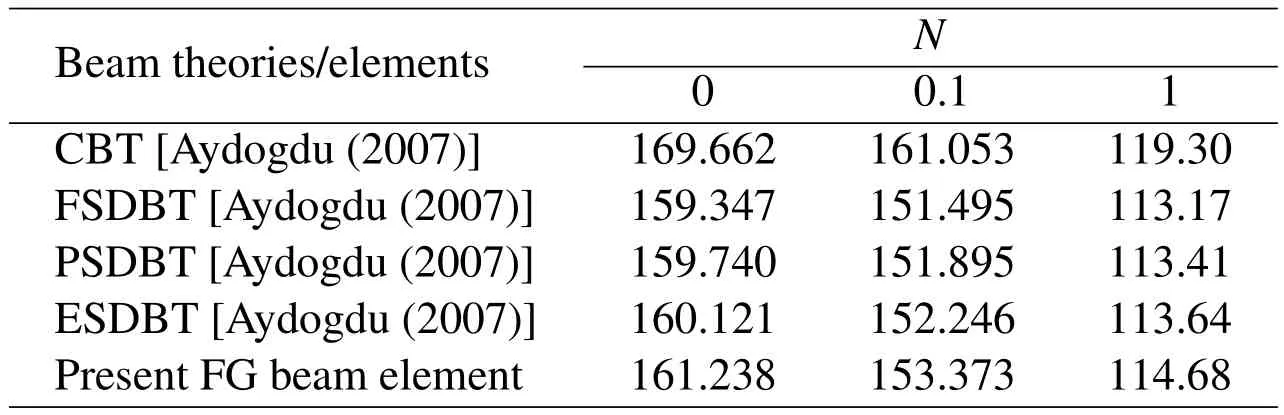
Table 6:Non-dimensional frequencies of the fifth-mode of simply supported FG beam given by different theories

7.2 Influence of temperature on frequencies of FG beams

Some examples are solved for the prediction of natural frequencies of the present FG beams under thermal loadings.A movable simply-supported Si3N4/SUS304 FG beam withL=2m,h=0.1m,b=0.1m[Shen and Wang(2014)]is considered.20 elements are used in the present FEA.Table 7 and Table 8 tabulate the results of the first three non-dimensional natural frequencies of Si3N4/SUS303 FG beams(L/h=20)under thermal environments obtained from the present FG beam element and the analytical solutions given by Shen and Wang(2014).The nondimensional frequency in the tables is defined asUnder a uniform thermal environment,the present results agree with the results of Shen and Wang(2014).However,under the non-uniform thermal environment,the natural frequencies given by the present FG beam element are different from the results of Shen and Wang(2014),particularly the difference between the results of Mode 1 of the FG beam withN=5 are significant.Therefore,a numerical analysis for the problem under consideration using ANSYS was carried out by the authors to check the accuracy of these two results.40 laminae across the FG beam thickness are used in the ANSYS computational model to ensure the accuracy of the numerical results.Each lamina in the equivalent multilayered beam model of the FG beam is meshed by two layers of Plane183 elements,and 800 elements are used along the beam axial direction.A mesh of 80 x 800 in the equivalent multilayered model of the FG beam is fine enough to obtain an accurate numerical result.The ANSYS results in Table 8 indicate that the present results are correct.

Table 7:Comparisons of non-dimensional natural frequencies for Si3N4/SUS304 FG beams under uniform thermal loading

Because of the inhomogeneity,the temperature field affects the dynamic behavior of FG beams.Fig.13 illustrates the effects of uniform thermal loading and non-uniform thermal loading on the fundamental frequencies of Si3N4/SUS303 FG beams withN=2.The aspect ratio of the FG beam isL/h=20,and the beam is modeled by 20 beam elements.It can be seen from Fig.13 that the fundamental frequencies decrease with the increase in temperature,and a uniform thermal loading has a more significant influence on the fundamental frequencies of the Si3N4/SUS303 FG beam than the given non-uniform thermal loading.

Table 8:Comparisons of non-dimensional natural frequencies for Si3N4/SUS304 FG beams under non-uniform thermal loading

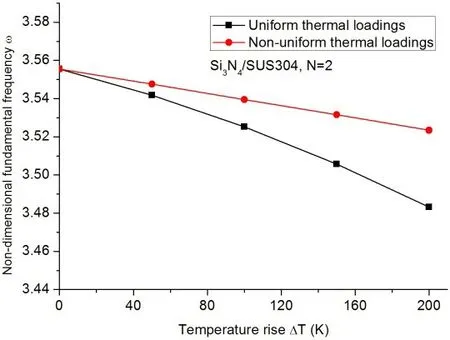
Figure 13:Non-dimensional fundamental frequencies of Si3N4/SUS304 FG beams with N=2 under uniform thermal loading and non-uniform thermal loading

8 Conclusion

This paper presents the analytical and FE modeling of FG beams for the static and dynamic analyses of the FG beams with thermoelastic coupling.The governing equations of FG beams are derived by using a re fined third-order shear deformation beam theory and the variational principle.An accurate and reliable two-noded beam element is developed based on the refined third-order shear deformation beam theory and the quasi-conforming element technique.The analytical solutions of the bending problems of FG beams under thermal loading are solved using the present governing equations of FG beams.A number of numerical examples of the bending and free vibration of FG beams with thermoelastic coupling are solved by the two-noded FG beam element,and the accuracy of the present numerical results is validated with the results reported in the literature or the 2D finite element results solved by the authors.Both the analytical solutions and the numerical results show that the analytical model and the FG beam element presented in this work have the following features.

1.The geometric middle surface of FG beams can be efficiently used as the reference surface,i.e.the surface withz=0,in the chosen re fined thirdorder shear deformation beam theory to achieve accurate results in the static and dynamic thermoelastic analyses of FG beams with different values of the volume fraction index and thermoelastic coupling.

2.The two noded FG beam element given in this study is not only efficient,but also capable of yielding very accurate stresses and frequencies of highermode vibration of FG beams with thermoelastic coupling,although merely a coarse mesh of beam elements is used in the numerical analysis.

Acknowledgement:The financial support provided by the grant of NSFC-91230113 is thankfully acknowledged.

Aydogdu,M.;Taskin,V.(2007):Free vibration analysis of functionally graded beams with simply supported edges.Mater.Design.,vol.28,pp.1651–1656.

Birman,V.;Byrd,L.W.(2007):Modeling and analysis of functionally graded materials and structures,Appl.Mech.Rev.,vol.60,no.5,pp.195–216.

Chakraborty,A.;Gopalakrishnan,S.;Reddy,J.N.(2003):A new beam finite element for the analysis of functionally graded materials.Int.J.Mech.Sci.,vol.45,no.3,pp.519–539.

Dong,L.;El-Gizawy,A.S.;Juhany,K.A.;Atluri,S.N.(2014a):A simple locking-alleviated 4-node mixed-collocation finite element with over-integration,for homogeneous or functionally-graded or thick-section laminated composite beams.CMC:Computers Materials&Continua,vol.40,no.1,pp.49–77.

Dong,L.;El-Gizawy,A.S.;Juhany,K.A.;Atluri,S.N.(2014b):A simple locking-alleviated 3D 8-Node mixed-collocation C0 finite element with over-Integration,for functionally-graded and laminated thick-section plates and shells,with&without Z-Pins.CMC:Computers Materials&Continua,vol.41,no.3 pp.163–192.

Ebrahimi,F.;Salari,E.(2015):A semi-analytical method for vibrational and buckling analysis of functionally graded nanobeams considering the physical neutral axis position.CEMS:Computer Modeling in Engineering&Sciences,vol.105,no.2,pp.151–181.

Giunta,G.;Crisafulli,D.;Belouettar,S.;Carrera,E.(2013):A thermomechanical analysis of functionally graded beams via hierarchical modelling.Compos.Struct.,vol.95,no.1,pp.676–690.

Kadoli,R.;Akhtar,K.;Ganesan,N.(2008):Static analysis of functionally graded beams using higher order shear deformation theory.Appl.Math.Model.,vol.32,no.12,pp.2509–2525.

Lü,C.;Chen,W.;Xu,R.;Lim,C.W.(2008):Semi-analytical elasticity solutions for bi-directional functionally graded beams.Int.J.Solids Struct.,vol.45,no.1,pp.258–275.

Mahi,A.;Adda Bedia,E.A.;Tounsi,A.;Mechab,I.(2010):An analytical method for temperature-dependent free vibration analysis of functionally graded beams with general boundary conditions.Compo.Struct.,vol.92,no.8,pp.1877–1887.

Noda,N.(1999):Thermal stresses in functionally graded materials.J.Therm.Stresses,vol.22,no.4,pp.477–512.

Ray,M.C.;Dong,L.;Atluri,S.N.(2015):Simple efficient smart finite elements for the analysis of smart composite beams.CMC:Computers Materials&Continua,vol.37,no.2,pp.65–99.

Reddy,J.N.;Chin,C.D.(1998):Thermomechanical analysis of functionally graded cylinders and plates.J.Therm.Stresses,vol.21,no.6,pp.593–626.

Sankar,B.V.;Tzeng,J.T.(2002):Thermal stresses in functionally graded beams.AIAA J.,vol.40,no.6,pp.1228–1232.

Shen,H.;Wang,Z.(2014):Nonlinear analysis of shear deformable FGM beams resting on elastic foundations in thermal environments.Int.J.Mech.Sci.,vol.81,no.4,pp.195–206.

Shi,G.;Voyiadjis,G.Z.(1991):Simple and efficient shear flexible two-node arch/beam and four-node cylindrical shell/plate finite elements.Int.J.Num.Meth.Eng.,vol.31,pp.759–776.

Shi,G.;Lam,K.Y.;Tay,T.E.(1998):On efficient finite element modelling of composite beams and plates using higher-order theories and an accurate composite beam element.Compos.Struct.,vol.41,no.2,pp.159–165.

Shi,G.;Voyiadjis,G.Z.(2011):A sixth-order theory of shear deformable beams with variational consistent boundary conditions.J.Appl.Mech.,vol.78,no.2,pp.856–875.

Simsek,M.(2009):Static analysis of a functionally graded beam under a uniformly distributed load by Ritz method.Int.J.Eng.Appl.Sci.,vol.1,no.3,pp.1-11.

Tang,L.;Chen,W.;Liu,Y.(1980):Quasi-conforming element for finite element analysis.J.Dalian Inst.Tech.,vol.19,no.2,pp.19–35.(in Chinese)

Thai,H.T.;Kim,S.E.(2015):A review of theories for the modeling and analysis of functionally graded plates and shells.Compos.Struct.,vol.128,pp.70–86.

Touloukian,Y.S.(1967):Thermophysical Properties of High Temperature Solids Materials.New York,MacMillan.

Wang,X.;Shi,G.(2012):The boundary layer solutions induced by displacement boundary conditions of shear deformable beams and accuracy study of higher-order beam theories.J.Eng.Mech.AMCE,vol.138,no.11,pp.1388–1399.

Wang,X.;Shi,G.(2013):A new assumed strain beam element based on a sixthorder beam theory for static and dynamic analysis of composite beams.APCOM&ISCM,11–14th December,Singapore.

Wattanasakulpong,N.;Gangadhara,P.B.;Kelly,D.W.(2011):Thermal buckling and elastic vibration of third-order shear deformable functionally graded beams.Int.J.Mech.Sci.,vol.53,no.9,pp.734–43.

Zhang,B.;He,Y.;Liu,D.;Gan,Z.;Shen,L.(2014):Size-dependent functionally graded beam model based on an improved third-order shear deformation theory.Eur.J.Mech A-Solid.,vol.47,pp.211-230.

Zhang,D.(2013):Nonlinear bending analysis of FGM beams based on physical neutral surface and high order shear deformation theory.Compos.Struct.,vol.100,no.5,pp.121–126.

Zhong,Z.;Yu,T.(2007):Analytical solution of a cantilever functionally graded beam.Compos.Sci.Technol.,vol.67,no.3,pp.481–488.

Zuo,H.;Yang,Z.B.;Chen,X.F.;Xie,Y.;Zhang,X.W.;Liu,Y.(2014):Static,free vibration and buckling analysis of functionally graded beam via B-spline wavelet on the interval and Timoshenko beam theory.CEMS:Computer Modeling in Engineering&Sciences,vol.100,no.6,pp.477–506.

1Department of Mechanics,Tianjin University,Tianjin,China

2Corresponding author.E-mail:shi_guangyu@163.com