A Metamodel-Based Global Algorithm for Mixed-Integer Nonlinear Optimization and the Application in Fuel Cell Vehicle Design

Haoxiang Jie,Huihong Shi,Jianwan Ding,Yizhong Wu,Qian Yin

A Metamodel-Based Global Algorithm for Mixed-Integer Nonlinear Optimization and the Application in Fuel Cell Vehicle Design

Haoxiang Jie1,2,Huihong Shi3,Jianwan Ding2,4,Yizhong Wu2,Qian Yin2

This paper improves the adaptive metamodel-based global algorithm(AMGO),which is presented for unconstrained continuous problems,to solve mixed-integer nonlinear optimization involving black-box and expensive functions.The new proposed method is called as METADIR,which can be divided into two stages.In the first stage,the METADIR adopts extended DIRECT method to constantly subdivide the design space and identify the sub-region that may contain the optimal value.When iterative points gather into a sub-region to some extent,we terminate the search progress of DIRECT and turn to the next stage.In the second phase,a local metamodel is constructed in this potential optimal sub-region,and then an auxiliary optimization problem extended from AMGO is established based on the local metamodel to obtain the iterative points,which are then applied to update the metamodel adaptively.To show the performance of METADIR on both continuous and mixed-integer problems,numerical tests are presented on both kinds of problems.The METADIR method is compared with the original DIRECT on continuous problems,and compared with SO-MI and GA on mixed-integer problems.Test results show that the proposed method has better accuracy and needs less function evaluations.Finally,the new proposed method is applied into the component size optimization problem of fuel cell vehicle and achieves satisfied results.

Metamodel;Black-box function;Mixed-integer nonlinear optimization;Fuel cell vehicle.

1 Introduction

Withthedevelopmentofcomputertechnique,engineerscanadoptavarietyofmodeling and simulation software to construct accurate analysis models of different fi elds,such as Computational Fluid Dynamics models[Li,Zhao,and Ni(2013)].and Finite Element Analysis models[Jie,Wu,and Ding(2014)].These simulation models generally have higher complexity and cost a lot of computation overhead.So when solving the optimization design involving these simulation models,the metamodel technique is usually adopted to approximate the expensive black-box analysis model in order to reduce the computational cost and shorten the design cycle.And the metamodel-based optimization algorithm has been well studied and widely used in dealing with continuous variable problems for the last 30 years[Gu,Li,and Dong(2012);Donald,Schonlau,and Welch(1998);Wang andShan(2007);Wu,Luo,Zhang,and Zhang(2014)].However,the study about applying the metamodel technique into the mix-integer optimization is a new area of optimization method based on metamodel technique.And it has gradually aroused the interest of researcher in recent six years.Hemker,De Gersem,von Stryk,and Weiland(2008)took use of surrogate model to approximate the simulation based objective function in the optimization design of superconductive magnet and then employed the branch and bound method the deal with the approximate MINLP.Holmström,Quttineh,Edvall(2008)extended the adaptive RBF method into mixed-integer constrained problems,and adopted the commercial TOMLAB optimization environment to solve the sub-MINLPs in the search process.Davis and Ierapetritou(2009)applied the Kriging and RSM metamodel into the branch and bound framework to solve problems with continuous and binary variables.Rashid,Ambani,and Cetinkaya,(2012)took use of multi-quadric RBF metamodel to approximate the actual expensive model and construct two auxiliary MINLP to determine the iterative points.SO-MI method was presented by Müller,Christine,and Piché(2013)to deal with the mixed-integer nonlinear problems involving expensive black-box functions.In SO-MI,Müller adopted the random sampling strategy for determining the iterative points rather than using the conventional MINLPs sub-solvers.

In this paper,we propose a metamodel based optimization method to solve the MINLPinvolvingblack-boxandexpensivefunctions,whichiscalledasMetamodel-Direct method for MINLP(METADIR).The new proposed method can be divided into two stages and is the extension of the adaptive metamodel-based global algorithm(AMGO)[Jie,Wu,and Ding(2014)],which is presented to deal with unconstrained continuous problems.In the first stage,the METADIR method firstly adopts improved DIRECT algorithm to subdivide the design space and identify the sub-region that may contain the optimal value.When the iterative points gather into the potential optimal sub-region to some extent,we terminate the subdivision and turn to the second phase.In this stage,the local metamodel is constructed in this sub-region.Then an auxiliary MINLP problem,extended from AMGO,is established based on the local adaptive metamodel to obtain the iterative points.Repeatedly update the metamodel using the iterative points,and finally the approximate optimal solutions are obtained when meeting the terminal conditions.Numerical tests are presented on both continuous and mixed-integer problems.The METADIR method is compared with original DIRECT method on continuous problems and compared with GA and SO-MI methods on MINLP problems.Tests result show that the proposed method has satisfactory accuracy and cost less function evaluations.Finally,the new proposed method is applied into the component size optimization problem of fuel cell vehicle and achieves satisfied results.

The remainder of the paper is organized as follows:The basic terminology involved in the algorithm will be described in section 2;Section 3 will detail the new proposed method;In section 4,we will give the numerical tests of the algorithm and the engineering application is given in section 5.Finally,the conclusions will be presented in section 6.

2 Basic terminology

2.1 Mixed integer nonlinear programs(MINLP)

The generalized MINLP problem can be expressed as below:

Where the design variablesX=[x,y]∈Rd,xandyare continuous and integer variables respectively,and wheref(x,y),g(x,y)are the objective function and constraint functions that may be nonlinear and multimodal,xl,ylandxu,yudenote thelowerandupperboundsofthevariables,nisthenumberoftheintegervariables.In this paper,we assume thatf(x,y),g(x,y)are defined and deterministic for allX∈[Xl,Xu].So the relaxation problem of the MINLP in equation(1)can be given as:

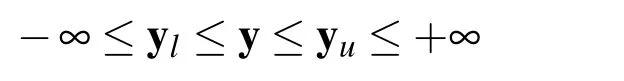
2.2 RBF metamodel

In this paper,the RBF metamodel is adopted to approximate the original expensive function.Radial basis function is an interpolation model using a weighted sum of simple basis functions attempting to emulate a complex or black-box function[Broomhead and Lowe 1988].The RBF metamodel is easy to construct,and can disposehighdimensionandhighorderproblemseffectively.Krishnamurthy(2003)presented the polynomial augmented RBF,which can provide better approximating precision.The RBF model with second-order polynomial we adopted can be described as:

Wherexis design variable of n dimension,andPr(x)is the monomial term in the second-order polynomial and γris the coefficient corresponding toPr(x).The number of polynomial coefficients ism=(n+1)(n+2)/2.The points which are sampled and evaluated can be described asS={x1,x2,...,xN},andrw=‖x−xw‖;φ is the basis function and the most common basis functions are listed as following:

Linear φ(x)=x

Cubic φ(x)=(x+c)3

Thin plate spline φ(x)=x2ln(c∗x)

Gaussian φ(x)=e−c∗x2

2.3 AMGO method

The AMGO method is presented to solve unconstrained optimization involving expensive black-box function.The AMGO adopts LHD sample method to obtain the initial data,and then construct the initial metamodel.In the searching process,an auxiliary function,which is given in equation(4),is established to determine the iterative point.The iterative points are then used to update the metamodel.The steps above are repeated until meeting the terminal conditions.

whereLis the distance factor,andtis the exponent.The expression ofLis list below:

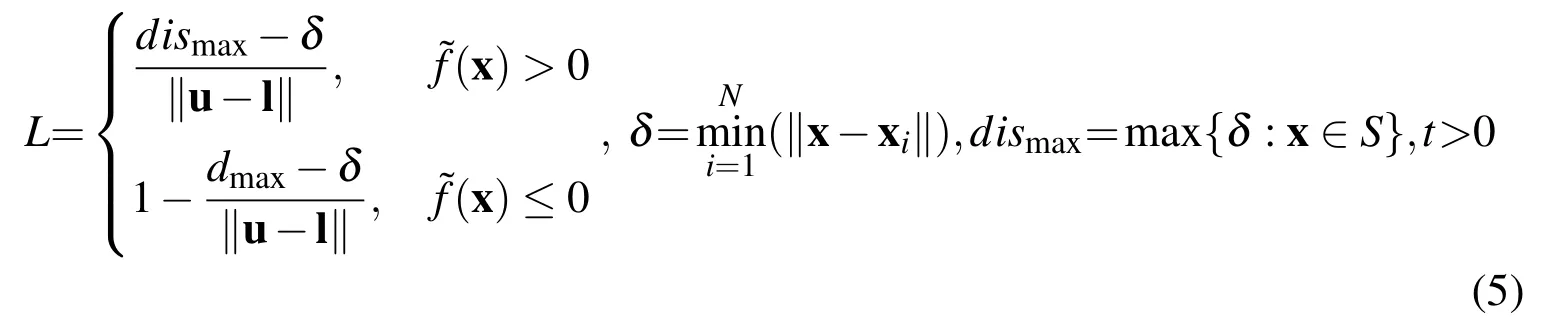
In equation(5),δ is the minimum distance between design pointxwith sampled pointsxi(i=1,2,...,N),anddismaxis the maximum distance among the sampled pointsxi(i=1,2,...,N).

The exponenttis applied to adjust the global and local search abilities of AMGO method in searching process.In each cycle,exponenttemploys a range of values(wherelis the length of distance exponent array τ ),starting from 0 to a larger one.

2.4 DIRECT algorithm method

The DIRECT algorithm is presented by Jones,Perttunen,and Stuckman(1993)based on lipschitz optimization,which doesn’t depend on the expression of objective function.The DIRECT is initially proposed to solve bound constrained problems and is then extended to handle with nonlinear constrained optimization described in(2)by optimizing the L1 penalty functions[Donald(2004)]given below:

where λ is a user-supplied penalty parameter

In the optimization process,DIRECT determines the Lipschitz constant adaptively to balance the global and local search ability.The basic thought of this method is:(1)Transform the search space to be unit hypercube.(2)Then trisect the search space,calculate the function valueof central point in each sub-hypercube and determine the potentially optimal sub-hypercube.(3)The potentially optimal rectangles will be further divided into smaller hypercube in which the central points will be samples.(4)Repeat(2–3)until the termination conditions is met.

3 Metamodel based method for mixed integer nonlinear optimization

In this work,the problems we studied are mix-integer nonlinear optimization involving black-box or expensive simulation based function.And if the constraints of the design problem are computation-intensive functions,they will be added into objective functions as Lagrange penalty terms.In the engineering application,some design problems are based on complex simulation models,such as CFD or FEAmodel,whichwouldcosthugecomputationaloverheadintheoptimizationdesign process and greatly increased the product development cycle.So our goal is to develop a global optimization algorithm that can obtain reasonably good solutions under less expensive function evaluations.The METADIR method firstly adopts the DIRECT algorithm to subdivide the original design space.As continually explore the design space,the sample points will gradually gather in to some subregion that contains the potential global minimum.However,the DIRECT method usually cost a lot of evaluation points to get convergence.So in METADIR,we stop the DIRECT process when the density of sample points in some region achieve to some extent,and take use of metamodel technique to establish a fine surrogate model in this local region.Then construct the auxiliary optimization problem according to the metamodel and update the metamodel.Repeat this procedure and fi nally we will obtain the approximate optimal solution of the original problem.In METADIR,the auxiliary function we established is extended from the AMGO method for unconstrained continuous problems.

3.1 DIRECT method for MINLP

The DIRECT method requires no knowledge of the information of objective function expression,and determines the iterative points barely based on current samples data.So it’s suitable for black-box functions or simulation based problems.In this work,the DIRECT algorithm is extended to solve the mixed-integer nonlinear problem.The main barrier when adopting original DIRECT in MINLP problem is that some of the variables are continuous but the others are discrete integer.So the improvement is mainly on the treatment of integer variable.In the DIRECT search process,the relaxed NLP(2)of original problem is solved firstly and then round the variablesyobtained.When dividing the hyper-rectangle,the length of hyper-cubic corresponding to integer variable is equal to the number of integer variable values.The basic steps of DIRECT method for MINLP can be described as:

Step 1.Construct the hyper-cubicH0according to the bound of variables,calculate center pointXc0.If theyofXc0is not integer,round theXc0.Set centerXc0as the initial sample point

Step 2.Compute the function valuef(Xc0),gi(Xc0)andF(Xc0),setfbest=f(Xc0)then initializek=0

Step 3.Add the initial hyper-cubic into the set of potential optimal hyper-cubicS.

Step 4.Repeat following steps until meet the termination condition

Step 4.1.For each hyper-cubicHjin setS,calculate the vectorof center pointXcjto rectangular vertexes.Take the modulevjofas the measure for the size of hyper-cubicHj.Obtain the dimension to subdivide theHjaccording to maximum component in.If the selected dimension to subdivide corresponds to the continuous variable,then trisect the hyper-cubicHj.However,if the selected dimension to subdivide corresponds to the integer variable,and

(a)If the number of possible value of the integer variablenum≥3,then symmetrically divide theHjinto three hypercube.

(b)If the number of possible value of the integer variablenum=2,then divide theHjinto two hypercube.

(c)If the number of possible value of the integer variablenum=1,then this dimension inHjwill no longer chosen to subdivide,and re-select the dimension to subdivideHjaccording to

Step 4.2.Calculate the center points of new hypercube obtained,and if theyof these center points are not integer,round these center points.Compute the function value of these points;sort these hypercube according to the function value of center points for each modulevj.

Step 4.3.Update thefbest,setk=k+1,and clear the set of potential optimal hyper-cubicS.

Step 4.4.For differentvj,select the hyper-cubic with minimal function value on center point into setS.

3.2 Local refine using metamodel-based method

In the search process of DIRECT,the iterative points will gradually gather into the area around current minimum.But it will cost many sample points when the sub-hypercube divided is small enough to terminate the search progress and obtain the optimal point.For optimization problem involving expensive function,this will bring great computational cost.Figure 1[Finkel(2003)]shows the distribution of sample points when solving GP function with DIRECT under 11 iterations.From fi gure 1,we can see that there are so many sample points located into the local area which contains the optimum before the algorithm stops.

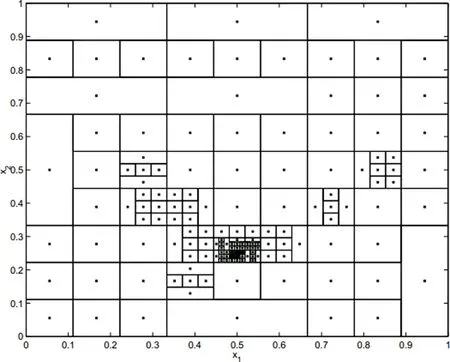
Figure 1:Distribution of sample points on GP.

In this paper,we consider when the sample points gather into some sub-region to some extent,an accurate metamodel is constructed to approximate the original expensive function in this local region.Then the metamodel based optimization method is applied to further refine the solution in this potential optimal area.Since the AMGO algorithm has a favorable performance in solving continuous problems,so we extend it to deal with MINLP problems to search the optimum in the local region.And the following auxiliary problem is then presented to obtain the iterative points.By continually updating the metamodel and solving this auxiliary problem,the approximate solution of original MINLP problem is obtained.

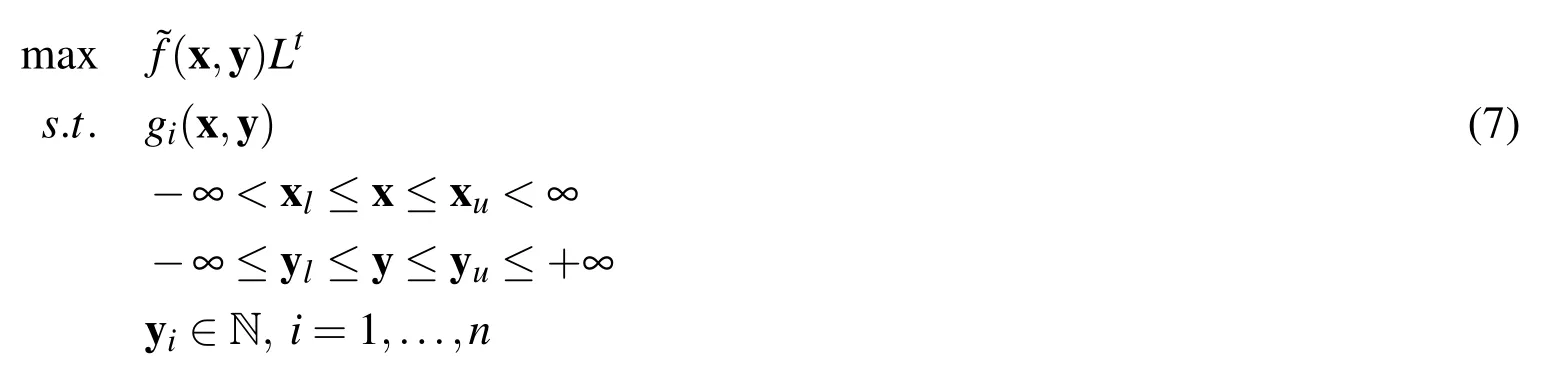
where the expression ofLand the description of exponenttare given in section 2.3.

3.3 Basic flow of the METADIR algorithm

In the new proposed algorithm,to ensure the final solution is feasible,one feasible point is required in the initial stage.Then the extended DIRECT method is applied to divide the design space and identify the potential optimal region.When detect a lot of sample points gathering into some local region,we stop the DIRECT search process and take use of metamodel to approximate the original problem in this local area.The density function of the sample points in the region is adopted to judge whether to terminate DIRECT search process and construct the accurate local surrogate model.The density function of the sample points in the region is defined as:

wheren(P)is the number of sample points in hyper cubicH,andV(H)is the hyper volume of hyper cubicH.

We calculate the hyper volume of hyper-cubic that contains the current best point and the 2dsample points closest to the current best point.Then the density function of this local region ρlocaland the average density function of the whole design space ρaveis obtained.If ρlocal≥ 5ρave,then terminate the DIRECT search process.The specific procedure and flow chart of the METADIR algorithm are given below.

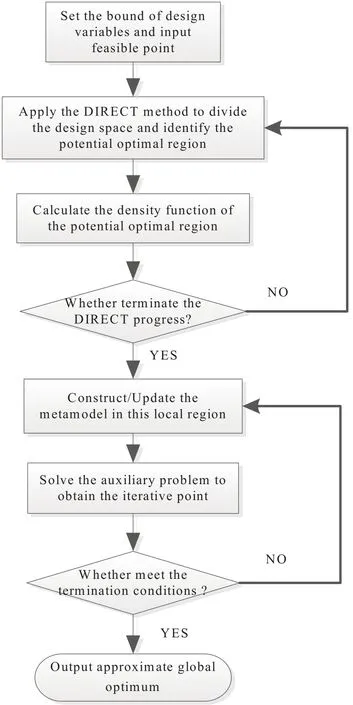
Figure 2:Flowchart of the METADIR method.

Step 1.Set the bound of design variables and input the known feasible points.

Step 2.Take use of extended DIRECT to continually divide the potential optimal region and update thefbest.

Step 3.Calculate the density function of sample points in current optimal region and decide whether terminate the DIRECT searching process.If yes,turn to step 4.Otherwise,turn to step 2.

Step 4.Construct/Update the local metamodel in the sub region.

Step 5.Solve the auxiliary problem in equation(7)to obtain the iterative points and update thefbest.

Step 6.Determine whether meeting the termination conditions?If yes,output the best point obtained;otherwise,turn to step 4.

4 Examples and discussion

In this section,the new proposed method is applied on four standard continuous numerical functions and compared with original DIRECT method,then a series of MINLP problems are chosen to test and compare the performance of the METADIR and the SO-MI methods.In the tests,we terminate the algorithms when the given maximal function evaluation number is achieved.All the experiments are performed on MatlabTM2014,the DIRECT toolbox is obtained from http://www4.ncsu.edu/eos/users/c/ctkelley/www/Finkel_Direct,and the SO-MI toolbox is provided at http://www.mathworks.com/matlabcentral/fileexchange/38530-surrogate-model-optimization-toolbox,and the GA code we used is the build-in version in global optimization toolbox in MatlabTM2014.In METADIR,the distance exponent array τ is set to be{0.01,0.1,1,10}.

4.1 Continuous problems

The functions we chosen to test the performance of proposed method on solving continuous problems are Branin,Hartman3,G4 and Pressure vessel design function.The Basic information of these functions is given in table 1.

Since DIRECT is a deterministic optimization method,we just need run one trial when test the performance of DIRECT on the benchmark functions.And 20 trials are performed on the new proposed method in order to reduce the effect of random error.Figures 3–6 show the search process of DIRECT method and the averaged optimal value obtained by the METADIR method.

Figures 3–6 demonstrate that the new proposed method performs better than DIRECT algorithm on the all test problems,and the accuracy and rate of convergenceby METADIR are both excel that by DIRECT.In the four continuous problems we adopted,Branin and Hartman3 are simple unconstrained functions,while G4 and PVD are nonlinear constrained problems.On Branin and Hartman3,tests result

show that the proposed method is slightly better than DIRECT on both accuracy and rate of convergence.From figure 5,we can see that DIRECT method cannot solve G4 problem effectively,while the METADIR method can rapidly converge around the global optimum after identifying the potential region.And as shown in fi gure 6,the accuracy and search rate of METADIR is much better than DIRECT on PVD function.

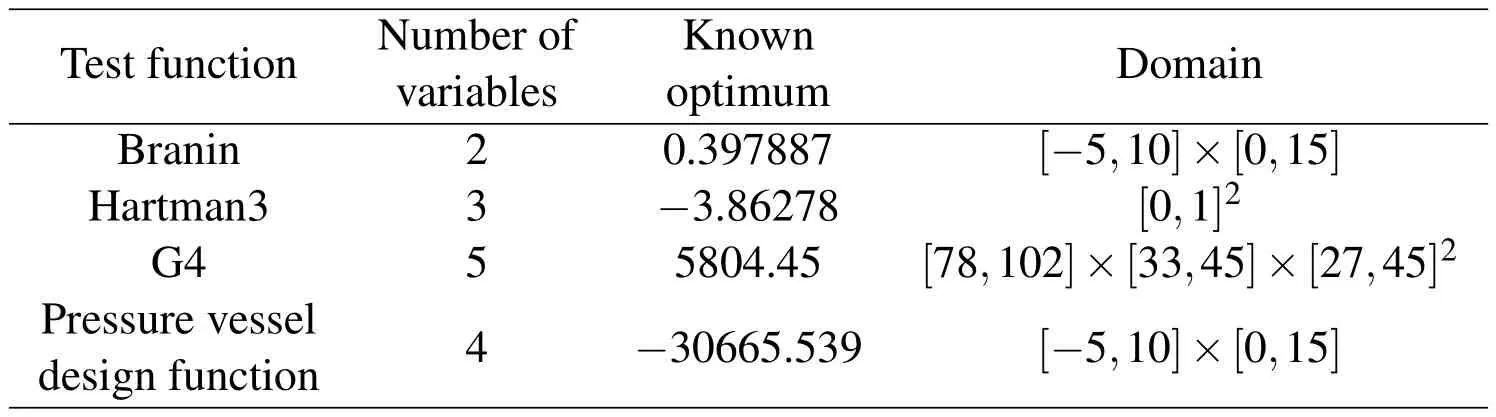
Table 1:Basic information of the continuous test problems.

Figure 3:Test results on Branin function.

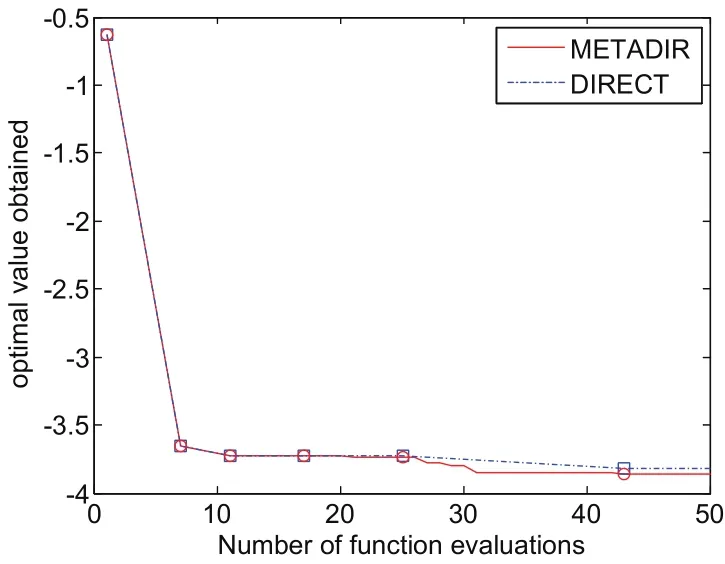
Figure 4:Test results on Hartman3 function.

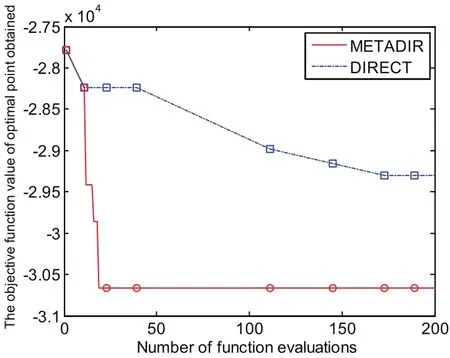
Figure 5:Test results on G4 function.

Figure 6:Test results on PVD function.

4.2 Mixed-integer problems

Inthispart,thenewproposedmethodistestedonaserialofmixed-integerproblems,and compared with the GA and SO-MI algorithms.These functions have already applied into the numerical test of Müller’s research[Jones,Donald R.(2004)].The expressions of these problems are given below:Problem 5

Problem 6

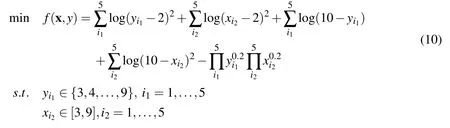
Problem 7

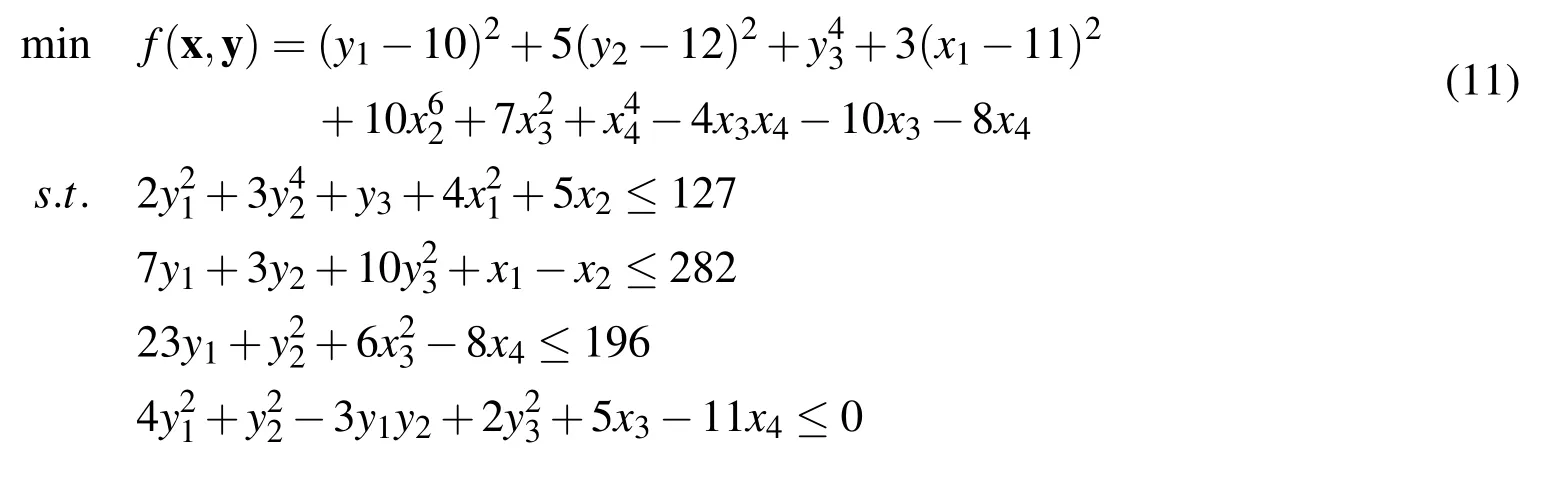
Problem 8

Problem 9

Problem 10

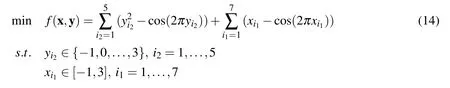
When testing on problems 5–10,the maximum number of function evaluations is set to be 200.For each test problem,20 trials are executed in order to reduce the effects of random error in test process.The mean and the standard deviation of optimum obtained by the three methods are given in table 2.In addition,the corresponding average number of function evaluation and the standard deviation are also calculated and listed.

Tests results in table 2 show that the new proposed method performs better than GA on all the six functions and better than SO-MI on problems 5–8.For problem 5,METADIR can rapidly converge,and the optimal point obtained by METADIR is better than that found by SO-MI and GA.When solving problem 6,the GA algorithm cannot found a satisfied solution under 200 function evaluations.But both METADIR and SO-MI can obtain an approximate optimal point,of which the function value is very close to global optimum.For test problem 7,the new proposed method is slightly better than SO-MI on both accuracy and search speed,while the performance of GA is very poor.Data in table also shows that METADIR can find significantly better solution than all other two methods on problem 8.When handling problems 9 and 10,SO-MI performs the best,and METADIR is slightly better than GA.On the test of problems 9 and 10,both GA and the new proposed method are not converge under the given function evaluation.

?

5 Application in component size optimization of fuel cell vehicle

Since the FCV is one of the most promising solutions to the atmospheric pollution andenergycrisis,theresearchaboutFCVhasattractedtheinterestofengineeringin modern automobile industry.In this section,the new proposed METADIR method is further applied into the component size optimization problem under ADVISOR platform.The configuration of Fuel Cell Vehicle is given in figure7 below:

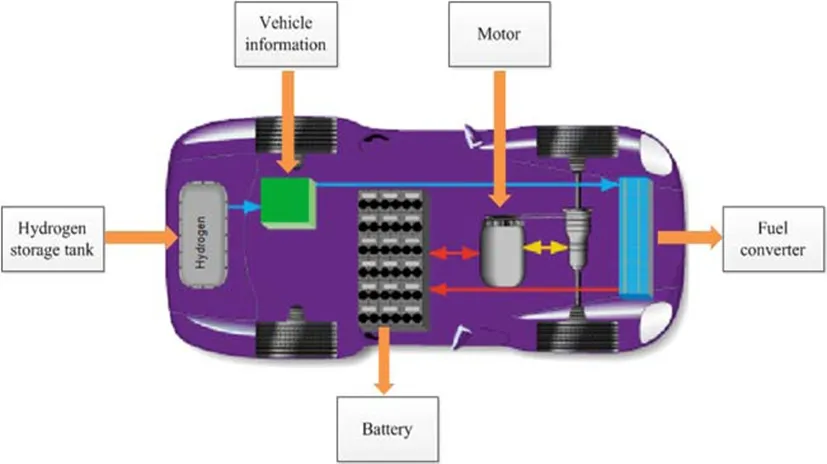
Figure 7:Configuration of Fuel Cell Vehicle.

5.1 Descriptions of FCV size optimization problem

In order to acquire better fuel economy and maintain satisfactory vehicle performance,the optimal design of component size of power system in FCV is very crucial.Since the optimization design based prototyping is expensive and time consuming,so simulation model based optimization process is widely used in modern vehicle design[Shiau and Michalek(2010)].ADVISOR is an effective simulation platform for vehicle design and analysis,which is developed by national renewable energy laboratory of USA based on Matlab/Simulink environment.The block diagram of the Fuel Cell Vehicle in ADVISOR is given in figure8:

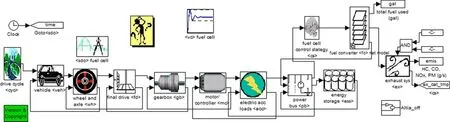
Figure 8:The block diagram of Fuel Cell Vehicle.

In this section,the goal of this optimization is to maximize the fuel economy of the vehicle under the given performance constraints,the detailed information about the design variables are listed in table 3.

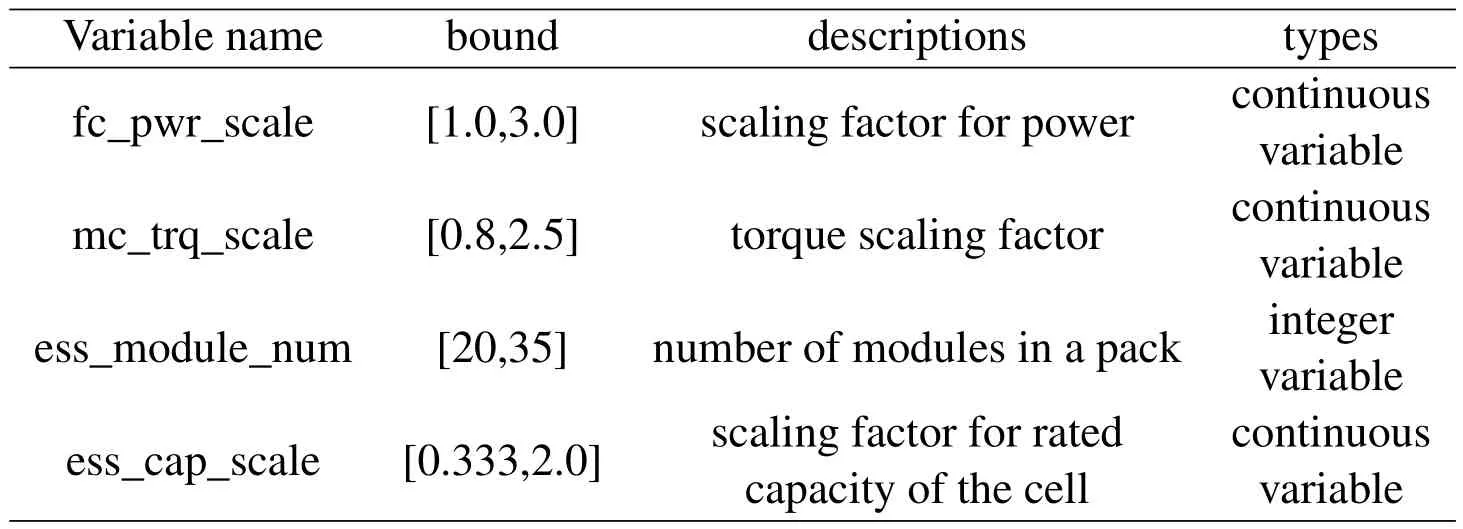
Table 3:Design variables.

And the optimization problem can be expressed as:

minf=FuelConsumption(x)

Subject to following constraints:

(1).The accelerationtime from 0–96.5km/h＜=11.2s

(2).The accelerationtime from 64–96.5km/h＜=4.4s

(3).The accelerationtime from 64–96.5km/h＜=20.0s

(4).The gradeability at 88.5km/h with 408kg cargo＞=6.5%

(5).Difference between requested speed and the actual speed at every second＜=3.2km/h

(6).Difference between final and initial battery state of charge(SOC)＜=0.5%

From the descriptions of the optimization problem above,it is can be seen that the analytical expressions of objective and constraint functions are unknown.The objectiveandconstraintfunctionvaluesareobtainedbyperformingthe“test_procedure”,“acceleration test”and “grade-ability test”simulation in Advisor platform.And the basic parameters of the test FCV is listed in table 4.

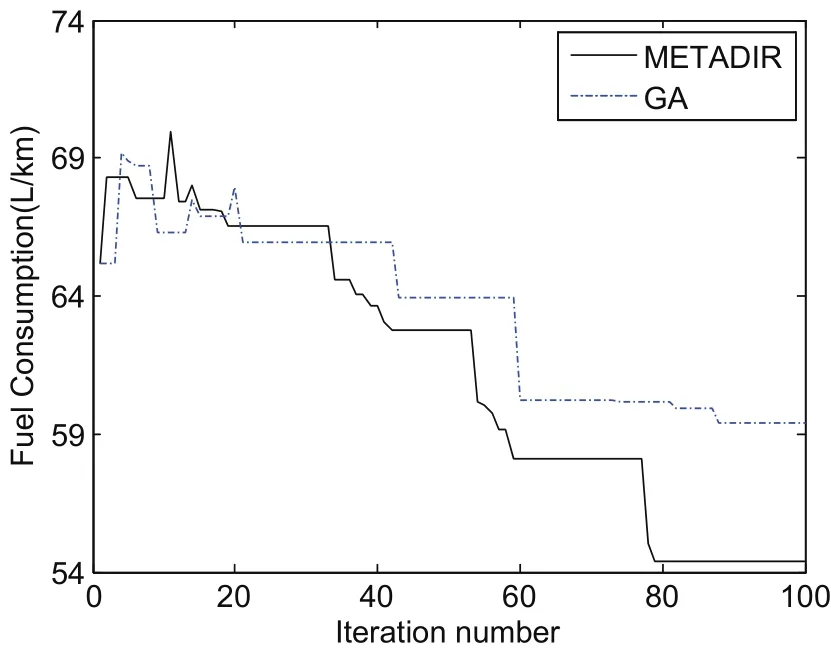
Figure 9:Iteration curve of FCV sizing optimization.

Table 4:Vehicle parameters.

5.2 Results and analysis

The new proposed method is compare with real-code GA algorithm in this optimal design,and the maximum number of iteration in METADIR and GA is set to 100.The number of population in GA is 20.The iteration curve is given in figure 9 and the performance of optimized vehicle model obtained by the METADIR and GA methods are given in table 5.

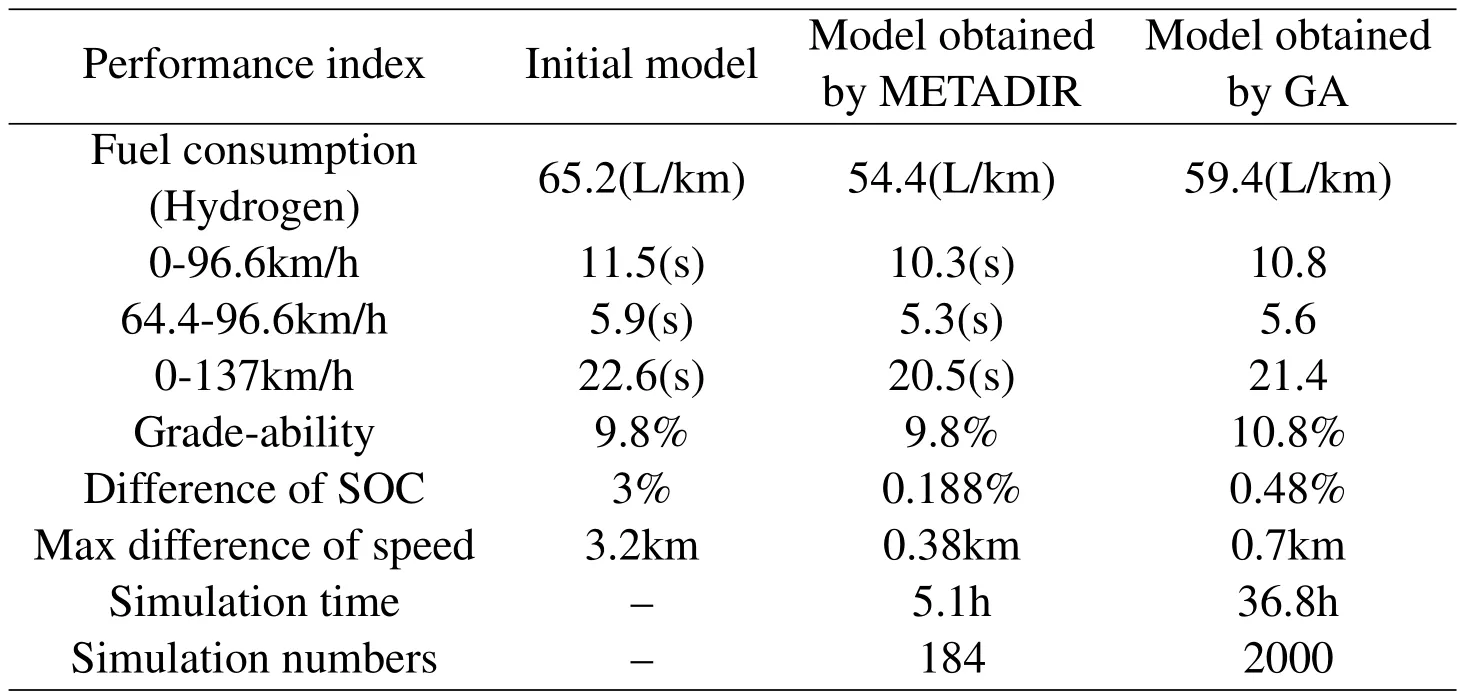
Table 5:Optimization Results.

It can be seen from table 5 that the new proposed METADIR method has better convergence performance than GA in solving the given sizing optimization problem.The fuel consumption of mode obtained by METADIR is 15.56%better than the initial model,and is 8.41%better than the model obtained by the GA method.And both the vehicle models obtained by METADIR and GA meet the given performance constraints.But the number of simulation and computational time cost by MEATDIR are both much lesser than that cost by GA.

Then the performance of vehicles obtained by GA and METADIR is further compared bellow.Figure 10 gives the working efficiency section of Fuel Converter,and fi gures 11–12 describe the discharging and charging ef fi ciency of storage batter.

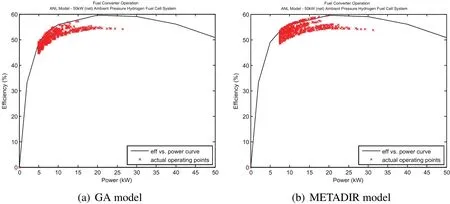
Figure 10:The scatter chart about Efficiency/Power of Fuel Converter.

From figure 10,it is can be seen that the working efficiency section of fuel converter of vehicle obtained by METADIR is better than that of vehicle obtained by METADIR.In addition,figure11 and figure12 show that the storage batter in GA vehicle model will conduct frequently charging and discharging when the FCV is running.However,the storage batter in METADIR vehicle model will discharge fi rstly,andwhentheSOCreducestosomeextent,thestoragebatterwillbecharged,which is bene fi cial to improve the working life of storage battery.

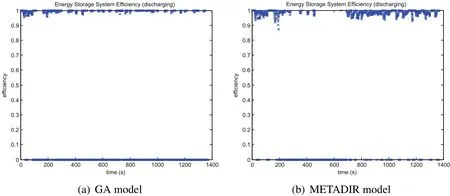
Figure 11:The scatter chart of storage batter discharging efficiency.

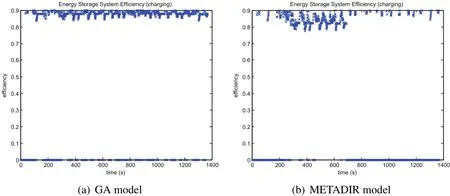
Figure 12:The scatter chart of storage batter charging efficiency.

6 Conclusions

Metamodel based method in solving optimization problems involving expensive function and mixed-integer design variables have gradually aroused researchers’interest.In this paper,an improved adaptive metamodel-based global algorithm named as METADIR is proposed to handle mixed-integer nonlinear optimization problems involving expensive black-box function.

In the searching process of METADIR,the improved DIRECT method is firstly applied to constantly subdivide the original design space and identify the potential optimal region.When the sample points gather around the current optimal point to some extent,we terminate the subdivision and turn to construct local metamodel in the potential optimal region obtained.In METADIR,the density function of the sample points in the region is adopted to decide whether to stop the subdivision process.After establishing the metamodel,the auxiliary function of AMGO is extended into MINLP problems to determine the iterative points,and the new data are then applied to update the metamodel.

The new proposed method is firstly compared with original DIRECT in solving continuous problems.Test results show that the METADIR method can better handle with the given four numerical functions,and the computational cost of METADIR is also less than original DIRECT.Then the METADIR is tested on six mixed-integer functions,and compared with SO-MI and GA methods.In the trials,the new proposed method performs better than GA on all the six test problems,and exceeds SO-MI on 4 out of six benchmark functions.Finally,the METADIR is applied to solve the sizing optimization problem in fuel-cell vehicle along with GA.The experiments indicated that the proposed method can obtain a slightly better solution than GA under less function evaluations.

In summary,this algorithm has a satisfactory precision and low computational cost,which makes it can widely applied in design optimization problems with black-box function involving continuous or mix-integer design variables.

Acknowledgement:ThisworkissupportedbytheNationalNatureScienceFoundation of China[number 51575205]and National High Technology Research and Development Program(863 Program)of China[number 2013AA041301].

Broomhead,D.S.;Lowe,D.(1988):Radial basis functions,multi-variable functional interpolation and adaptive networks:DTIC Document.

Davis,E.;Ierapetritou,M.(2009): A kriging based method for the solution of mixed-integer nonlinear programs containing black-box functions.Journal of Global Optimization,vol.43,no.2–3,pp.191–205.doi:10.1007/s10898-007-9217-2

Finkel,D.E.(2003): DIRECT Optimization Algorithm User Guide.from http://www4.ncsu.edu/eos/users/c/ctkelley/www/Finkel_Direct/.

Gu,J.;Li,G.Y.;Dong,Z.(2012):Hybrid and adaptive meta-model-based global optimization.Engineering Optimization,vol.44,no.1,pp.87–104.

Hemker,T.;De Gersem,H.;von Stryk,O.;Weiland,T.(2008): Mixedinteger nonlinear design optimization of a superconductive magnet with surrogate functions.IEEE Transactions on Magnetics,vol.44,no.6,pp.1110–1113.doi:10.1109/TMAG.2007.916165

Holmström,K.;Quttineh,N.-H.;Edvall,M.(2008):An adaptive radial basis algorithm(ARBF)for expensive black-box mixed-integer constrained global optimization.Optimization and Engineering,vol.9,no.4,311–339.doi:10.1007/s11081-008-9037-3.

Jie,H.;Wu,Y.;Ding,J.(2014):An adaptive metamodel-based global optimization algorithm for black-box type problems.Engineering Optimization,ahead-ofprint,pp.1–22.doi:10.1080/0305215X.2014.979814.

Jones,D.R.;Perttunen,C.D.;Stuckman,B.E.(1993):Lipschitzian optimization without the Lipschitz constant.Journal of Optimization Theory and Applications,vol.79,no.1,pp.157–181.doi:10.1007/BF00941892.

Jones,D.R.(2004):DIRECT Optimization Algorithm User Guide addendum.from http://www4.ncsu.edu/eos/users/c/ctkelley/www/Finkel_Direct/.

Jones,D.R.;Schonlau,M.;Welch,W.J.(1998):Efficient global optimization of expensive black-box functions.Journal of Global Optimization,vol.13,no.4,pp.455–492.

Krishnamurthy,T.(2003):Response surface approximation with augmented and compactly supported radial basis functions.Paper presented at the Proceeding of the 44 th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.AIAA Paper.

Müller,J.;Shoemaker,C.A.;Piché R.(2013): SO-MI:A surrogate model algorithm for computationally expensive nonlinear mixed-integer black-box global optimization problems.Computers and Operations Research,vol.40,no.5,pp.1383–1400.doi:http://dx.doi.org/10.1016/j.cor.2012.08.022.

Rashid,K.;Ambani,S.;Cetinkaya,E.(2012):An adaptive multiquadric radial basis function method for expensive black-box mixed-integer nonlinear constrained optimization.Engineering Optimization,vol.45,no.2,pp.185–206.doi:10.1080/0305215X.2012.665450.

Li,S.;Zhao,F.;Ni,Q.-J.(2013):Multiobjective optimization for ship hull form design using SBD technique.CMES:Computer Modeling in Engineering and Sciences,vol.92,no.2,123–149.

Shiau,C.-S.N.;and Michalek,J.J.(2010):A MINLP Model for Global Optimization of Plug-In Hybrid Vehicle Design and Allocation to Minimize Life Cycle Greenhouse Gas Emissions.Paper presented at the ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.

Wang,G.G.;Shan,S.(2007):Review of metamodeling techniques in support of engineering design optimization.Journal of Mechanical Design,vol.129,no.4,pp.370–380.

Wu,J.;Luo,Z.;Zhang,Y.;Zhang,N.(2014): An interval uncertain optimization method for vehicle suspensions using Chebyshev metamodels.Applied Mathematical Modelling.

1No.711 Institute,China Shipbuilding Industry Corporation,Shanghai,China

2National CAD supported Software Engineering Centre,Huazhong University of Science and Technology,Wuhan,PR China

3Financial school,Capital University of Economics and business,Beijing,PR China

4corresponding author,Email:dingjw@mail.hust.edu.cn