Large Deformation Hyper-Elastic Modeling for Nonlinear Dynamic Analysis of Two Dimensional Functionally Graded Domains Using the Meshless Local Petrov-Galerkin(MLPG)Method

Mohammad Hossein Ghadiri Rad,Farzad Shahabian,2,Seyed Mahmoud Hosseini

Large Deformation Hyper-Elastic Modeling for Nonlinear Dynamic Analysis of Two Dimensional Functionally Graded Domains Using the Meshless Local Petrov-Galerkin(MLPG)Method

Mohammad Hossein Ghadiri Rad1,Farzad Shahabian1,2,Seyed Mahmoud Hosseini3

A meshless method based on the local Petrov-Galerkin approach is developed for elasto-dynamic analysis of geometrically nonlinear two dimensional(2D)problems in hyper-elastic functionally graded materials.The radial point interpolation method(RPIM)is utilized to build the shape functions and the Heaviside step function is used as the test function.The mechanical properties of functionally graded material are considered to continuously vary in a certain direction and are simulated using a nonlinear power function in volume fraction form.Considering the large deformations,it is assumed that the domain be made of large deformable neo-Hookean hyperelastic materials.Rayleigh damping is employed to model energy dissipation in analyses.The Newmark finite difference method is used to treat the time dependence of the variables.At any time step of Newmark method,the Newton-Raphson iteration technique is employed to solve the nonlinear governing equations.Accuracy of the proposed method is verified using the results available in the literature.It is shown that the present MLPG method is a suitable meshless method for large deformation problems.The nonlinear time histories and wave propagations of displacement field for various FG distributions and damping ratios are studied in detail.

MeshlesslocalPetrov-Galerkin(MLPG)method;Geometricallynonlinear problems;Functionally graded materials(FGMs);Neo-Hookean constitutive model;Nonlinear time history;Wave propagation analysis;Rayleigh damping.

1 Introduction

In recent decades,the meshless methods are being increasingly applied for various engineering problems.In these methods,the distributed nodes,rather than the meshing,are used for discretization of problem domain and its boundaries.A variety of meshless methods has been proposed by the researchers.Smooth particle hydro dynamics(SPH)[Gingold and Monaghan(1977)],reproducing kernel particle method(RKPM)[Liu,Jun,Li,Adee,and Belytschko(1995)],element-free Galerkin(EFG)[Belytschko,Lu,and Gu(1994)],meshless local Petrov-Galerkin method(MPLG)[Atluri and Zhu(1998)],local boundary integral equation(LBIE)[Atluri,Sladek,Sladek,and Zhu(2000)]and Meshless natural neighbor Galerkin method[Cai and Zhu(2004)],are the most popular meshless methods.Among these,the MLPG method due to its special characteristics has been widely used.In this method the governing equations are satisfied over the local sub-domains with arbitrary shapes.Since no elements or background cells are required neither for interpolation of the trial and test functions nor for integration of the local weak-form of governing equations,the MLPG method is known as a truly meshless method.In addition in this method,the test and trial functions can be selected from different functional spaces.A review has been presented for analysis of problems in various fields of engineering and scientific with the use of the MLPG method[Sladek,Stanak,Han,Sladek,and Atluri(2013)].

Developments in the field of materials engineering lead to a new type of materials with smooth and continuous variation from one material to the other,which are called functionally graded materials(FGMs).In some engineering designs,dynamical prediction and analysis of FG structures under shock loading is very important.Many researchers have focused on dynamic behavior of these structures using meshless methods.Sladek,Sladek,Zhang,and Schanz(2006)presented a meshless local Petrov-Galerkin method for static and dynamic analysis of continuously non-homogeneous and linear visco-elastic solids.Sladek,Sladek,Krivacek,Wen,and Zhang(2007)for the first time developed the MLPG method to solve dynamic plate bending problems described by the Reissner-Mindlin theory.Moussavinezhad,Shahabian,and Hosseini(2013)developed the meshless local Petrov-Galerkin method for two dimensional dynamic stress analyses in 2D-FG cylinders.Hosseini,Shahabian,Sladek,and Sladek(2011)studied on the effects of uncertainty in constitutive mechanical properties for functionally graded thick hollow cylinders.At the same year,Hosseini,Shahabian,Sladek,and Sladek(2011)successfully applied the MLPG method for coupled thermo-elasticity analysis of FG thick hollow cylinders based on Green-Naghdi theory.In another work,Hosseini,Sladek,and Sladek(2013)extended this method for analysis of non-Fick diffusion elasticity problems.The wave propagation of mass diffusion,temperature and elas-tic waves in two dimensional problems at various time instants are also presented and discussed in details by Hosseini,Sladek,and Sladek(2014).Chen,Xu,and Tong(2015)applied the meshless local natural neighbour interpolation method to solve linear dynamic problems of FGMs in continuously heterogeneous and linear viscoelastic media.

In geometrically nonlinear analysis,changing in geometry as the structure undergoes the large deformations must be taken into account.Meshless methods due to their advantage in eliminating mesh distortion have been successfully employed for geometrically nonlinear analysis of solids.Hehua,Wenjun,Yongchang,and Yuanbin(2007)solved two dimensional problems with incompressible large deformation using meshless local natural neighbor interpolation method(MLNNIM).They presented the large-deformation formulae according to the both total Lagrangian(TL)and updated Lagrangian(UL)methods.Gu,Wang,and Lam(2007)developed the local Kriging meshless method for large deformation analyses of microelectro-mechanical systems[Lin,Naceur,Coutellier,and Laksimi(2014)].studied on shell structures undergoing very large deformations using the shell-based SPH method.A geometrically nonlinear dynamic meshless method for analysis of FG thick hollow cylinders is presented by Ghadiri Rad,Shahabian,and Hosseini(2015).In their study,because of large deformations,the neo-Hookean hyperelastic constitutive model was considered for the problem.In another work,Ghadiri Rad,Shahabian,and Hosseini(2015)developed the MLPG method for nonlinear dynamic analyses of FG thick hollow cylinder with Rayleigh damping.

The objective of this paper is to develop the well-known MLPG method for the solution of geometrically nonlinear dynamic equations in 2D domains.For this purpose the formulations are given in the Cartesian coordinate system in contrast with Ghadiri Rad,Shahabian,and Hosseini(2015)papers in which the cylindrical coordinate system was used.It should be mentioned that using the MLPG method with Heaviside test function in the Cartesian coordinate system leads to a set of differential equations needed to integrate only over the boundaries of sub-domains.The linear curve integration over the boundaries rather than the integration over the area of sub-domains,improve the accuracy and computational efficiency of the MLPG method especially in geometrically nonlinear dynamic analysis.The mechanical properties of FG material are simulated using a nonlinear power function.Considering the large deformations,it is assumed that the domain is made of large deformable neo-Hookean hyperelastic materials.The nonlinear equations of motion are obtained based on total Lagrangian approach.These equations are solved using the incremental-iterative Newmark/Newton-Raphson technique.Several numerical examples with various loadings and boundary conditions are presented to demonstrate the convergence and efficiency of developed method.The compari-son of numerical results with those reported in the literature shows that the MLPG method is very effective for the large deformation analyses.In this paper,the two dimensional nonlinear wave propagation of displacement field for various FG distributions and damping ratios are studied in details in addition to time history analysis.

2 Overview of the radial point interpolation method

In radial point interpolation method,the displacement function ‘u’at a point of interest‘xi’using ‘n’nodes located in its support domain ‘Ωs’can be approximated as follows:

where ‘uh’is the approximation of displacements,‘R’is a vector of radial basis function(RBF)and ‘a’is a vector of coefficients.Multi-quadric(MQ)function,exponential(Exp)function,thin plate spline(TPS)function and logarithmic radial basis function are the most commonly used RBFs.In this paper,the multi-quadrics(MQ)radial basis function is used which is defined as:

where ‘c’and ‘q’are the constant values which have to be determined using numerical investigations.

The radial point interpolation method(RPIM)obtains its approximation at any point of interest by letting the interpolation function pass through the function valuesateachscatterednode(fieldnode)withinthesupportdomainofpointofinterest[Liu and Gu(2005)].Thus,in order to determine the coefficient vector‘a’,the RPIM approximation should be satisfied at the all nodes located in support domain as follows:

where ‘Us’is a vector of nodal values of displacements and the moment matrix‘RQ’is a matrix of nodal values of RBFs at the all nodes in support domain.

Since the distance is directionless,the moment matrix is symmetric.By solving the Eq.(3)and then substituting into Eq.(1),the RPIM shape functions‘N’can be obtained as follows:

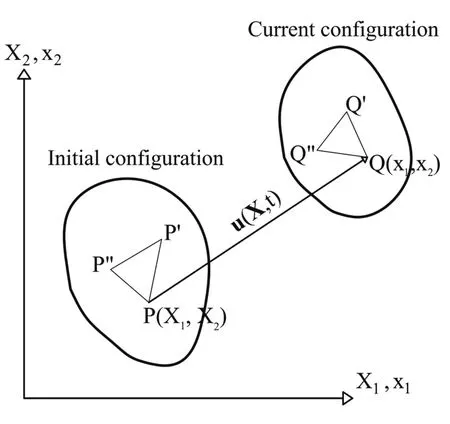
Figure 1:Two configurations of a body with finite deformation.

3 Geometrically nonlinear dynamic formulation

3.1 Kinematics

Fig.1 shows the initial and current configurations of a body.The relation between the current coordinates ‘xi’and the initial coordinates ‘Xi’of a point such as ‘P’is given by:

where,‘ui’denotes the displacement of point‘P’in the ‘i’direction.Using the Chain rule,the last equation can be differentiated as:

here,‘Fij’is the deformation gradient tensor which gives the relationship of a line‘dX’at the initial configuration to the line ‘dx’at the deformed configuration.

In this paper,a comma denotes the differentiation.The deformation gradient vector‘F’is defined as follow:

Differentiation of Eq.(9)and then replacing the displacement‘ui’with its approximation function from Eq.(6),leads to:

where

3.2 Strain-displacement relationship

The Green’s strain tensor‘εij’in the Cartesian coordinate system is given by:

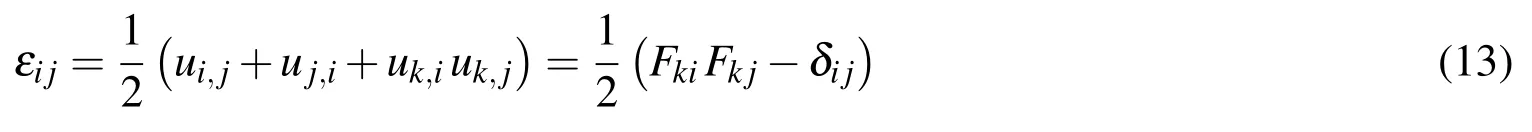
Using the Chain rule,one can obtain the differentiated form of Eq.(13)as:

The last equation can be rewritten in the following matrix form.

where

Finally,replacing ‘∆F’from Eq.(11),the Green’s strain-displacement relation can be obtained as follows:

where

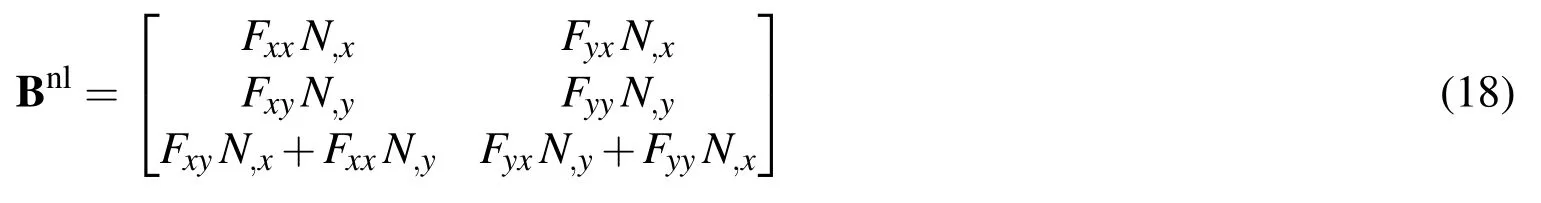
3.3 Constitutive relationship

For a hyper-elastic material the constitutive relationship can be derived from the strain energy function‘ψ(ε )’as:

Then,the fourth-order constitutive tensor can be obtained from:

Inthepresentstudy,acompressibleneo-Hookemodelisconsideredfortheproblem with the following strain energy function.

where ‘λ’and ‘µ’are the Lame constants,‘I1’stand for the first strain invariant and ‘J’is the determinant of deformation gradient tensor(J=det(Fij)).Using Eqs.(19)to(21),the second Piola-Kirchhof stress and constitutive tensors are given by[Gu,Wang,and Lam(2007)]:

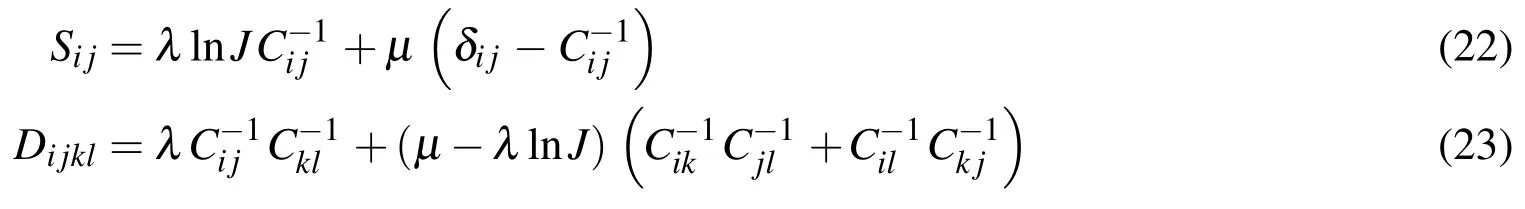
where

Using the constitutive tensor ‘Dijkl’and Strain-displacement relationship,the increment of second Piola-Kirchhof stress can be obtained with respect to the nodal displacements.

3.4 Elasto-dynamic governing equation

True loading and stresses exist only at the deformed configuration.Hence,the equilibrium equations of a body with large deformations must be written at the current configuration which is given by:

here,‘σji’is the Cauchy(real)stress tensor with the subscript notation which is interpreted as follows:the first letter represents the surface on which the stress is acting,and the second letter represents the direction of the stress. ‘bi’is the ‘i’directional body force per unit mass,‘ρ’is the mass density at the current configuration and‘¨ui’is the‘i’directional component of acceleration vector.Due to the deformed configuration is unknown,in order to solve Eq.(27),all quantities must be transferred to the solved configuration that can be either the initial configuration(TL)or the last known configuration(UL).Since in meshless methods the construction of the shape functions is performed during the analysis,using UL description needs more computational time.Thus,in this paper the formulation is done based on TL description.Using TL description,Eq.(27)can be transformed to the initial configurations,as follows:

where ‘ρ0’is the mass density at the initial configuration and ‘Pji’is the 1st Piola-Kirchhoff stress tensor.However,in order to use the more useful and symmetric second Piola-Kirchhoff stress tensor‘Sji’,the Eq.(28)can be transformed into:

The 1st and the second Piola-Kirchhoff stress tensors can be related to the Cauchy stress tensor as:

Following the weighted residual method,the weak form of Eq.(29)in a quadrature domain ‘Ωq’of an arbitrary node ‘xq’at the initial configuration can be obtained as follows:

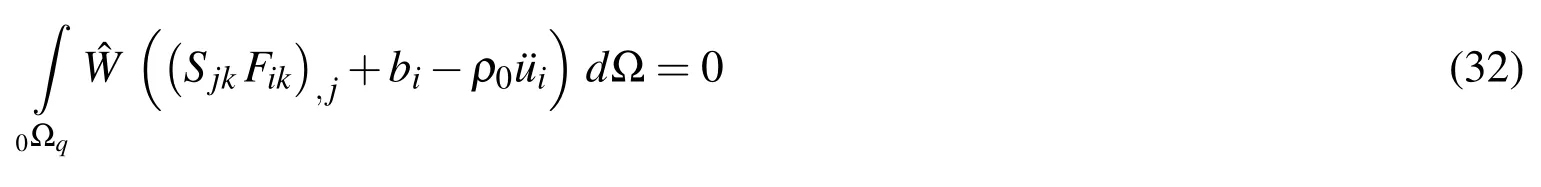
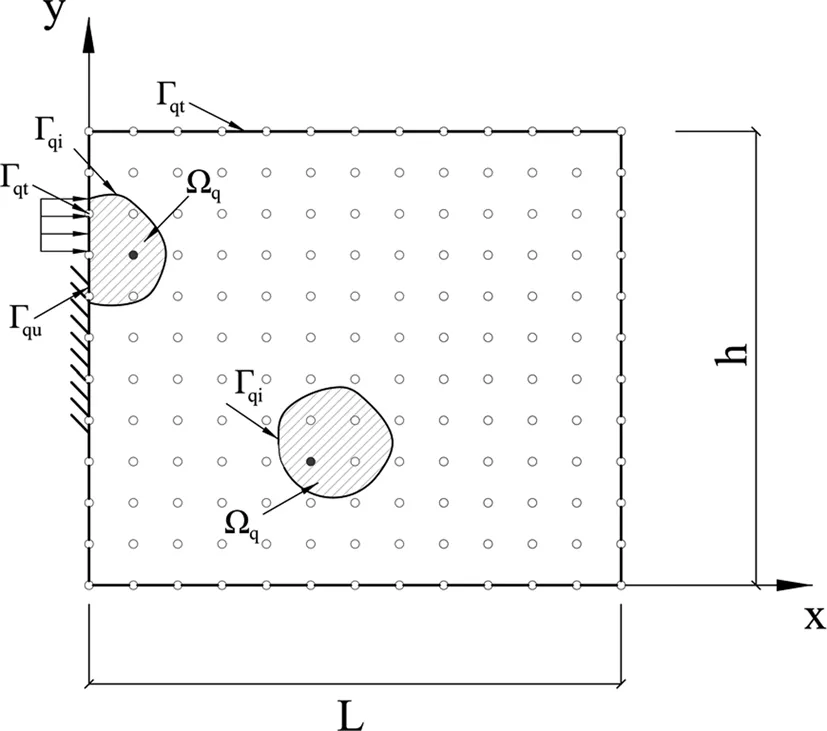
Figure 2:Local domains and their boundaries.

where(Γq= Γqi∪Γqu∪Γqt)and ‘Γqi’is the internal boundary,‘Γqu’is the essential boundary and ‘Γqt’is the natural boundary of local sub-domain ‘Ωq’(see Fig.2).In Eq.(13)‘Ti’is the ‘i’directional traction applied on the natural boundary ‘Γqt’.Using the chain rule,the incremental form of Eq.(33)can be obtained as:

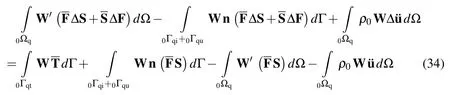
where‘∆S’,‘∆F’and‘∆¨u’respectively are the second Piola-Kirchhof stress,deformation gradient and acceleration increments from time ‘t’to ‘t+∆t’.The last equation can be rewritten in the following matrix form:

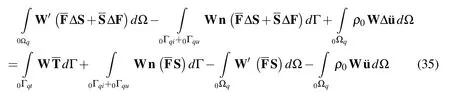
where

Replacing ‘∆F’and ‘∆S’from Eqs.(11)and(26)into Eq.(35),the incremental equation of motion at the time step ‘n’can be obtained as:

where‘∆’,‘∆’and‘∆un’are the incremental acceleration,velocity and displacement vectors,respectively. ‘M’and ‘KT’are the mass and tangent stiffness matrices and ‘∆Pn’is the equivalent nodal force vector which are defined as:

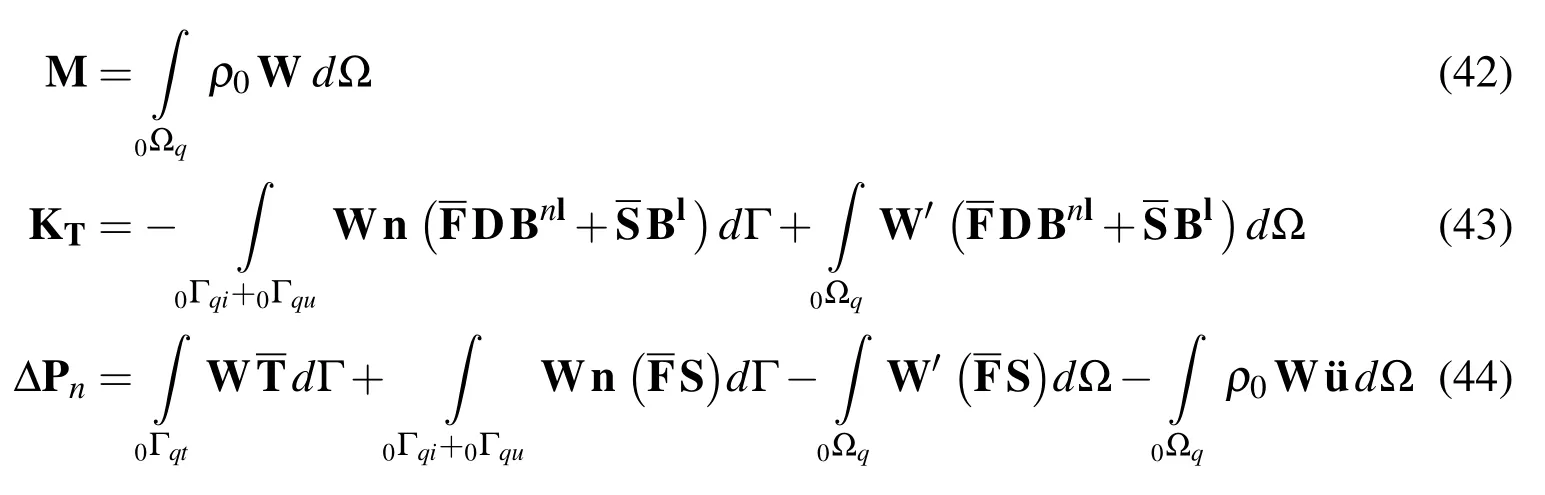
In this paper,the Rayleigh damping is employed to model the energy dissipation in the system.In this model the damping matrix is considered to be proportional of both stiffness and mass matrices.

where‘α’and ‘β’are the coefficients which can be determined from two specified damping ratios,using the following equation:

where ‘ωi’is the natural frequency of‘i’th mode.In this paper,both the first and second modes are assumed to have the same damping ratio ‘ξ’which is reasonable based on experimental data[Chopra(2001)].Thus,one can write:

4 Method of solution

4.1 Time steps

The equations of motion are solved using the Newmark/Newton-Raphson technique with suitable time steps.Newmark proposed the following approximation for velocity and acceleration at the ‘n’th time step[Chopra(2001)].

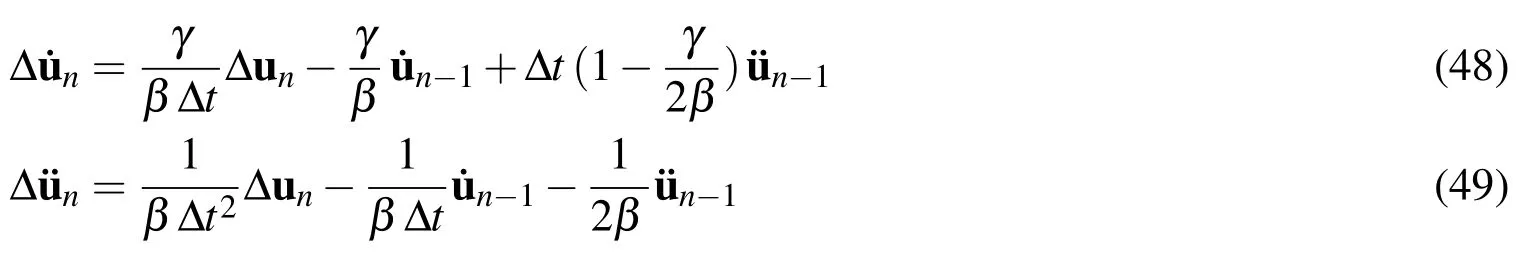
where ‘γ’and ‘β’are the Newmark’s parameters.The stability and convergence of this method can be achieved by typical choosing ‘γ=0.5’and ‘β =0.25’.Substitution Eqs.(48)and(49)into Eq.(41)yields Eq.(50).

With:

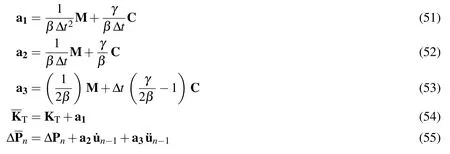
Since the Eq.(50)is nonlinear,the nodal incremental displacement vector‘∆un’must be computed using an iterative procedure which is presented in the next subsection.

4.2 Iteration steps

According to Eq.(50),it is necessary to solve the set of discretized equations for‘∆un’with the r.h.s.being dependent on the displacements‘un=un−1+∆un’.

Since‘∆Pn’isnonlinearfunctionof‘un’,itisnecessarytosolveEq.(50)iteratively,i.e.‘∆un’at‘k+1’iterative step is calculated from the equation:

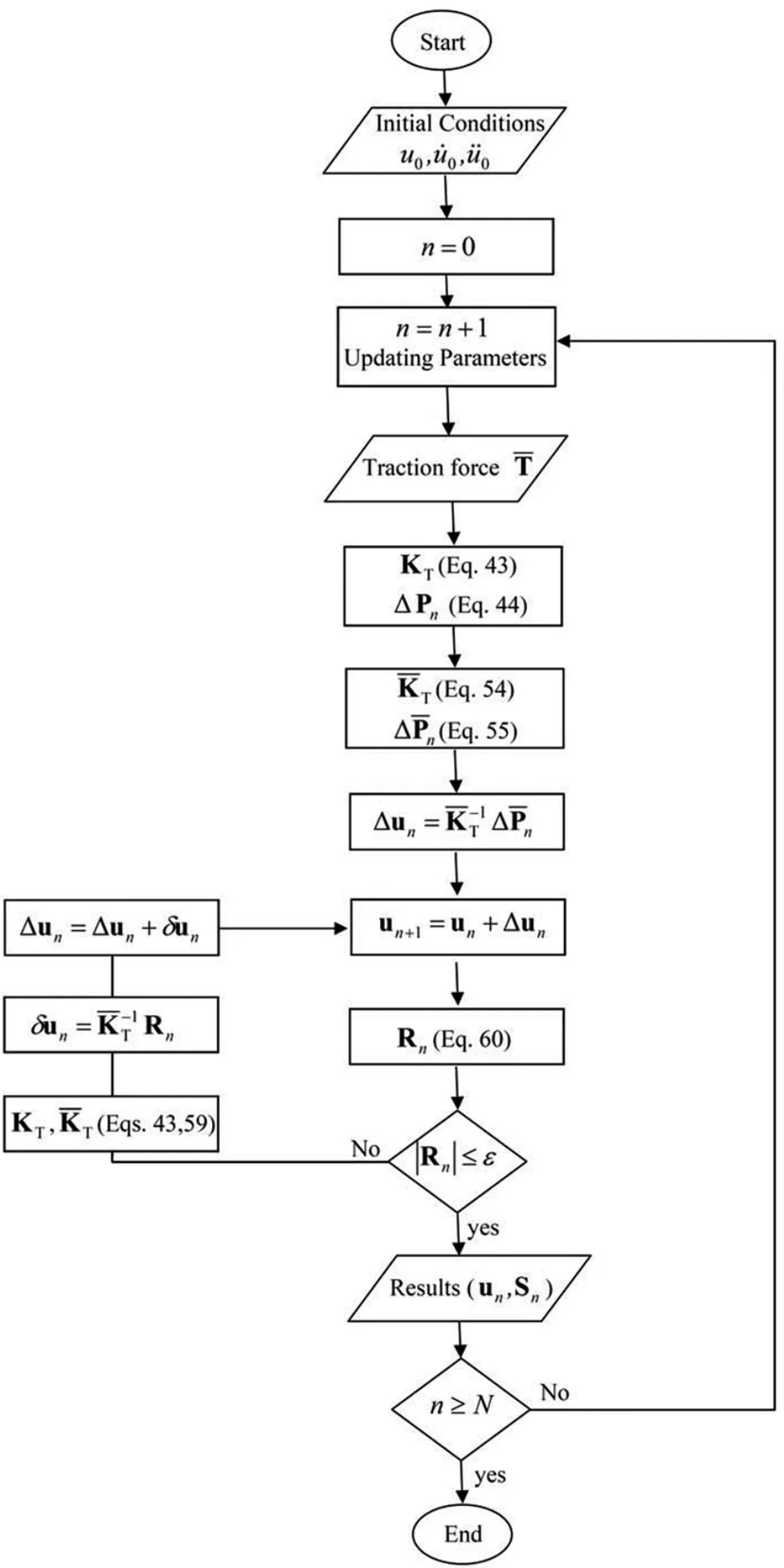
Figure 3:Flowchart of geometrically nonlinear dynamic analysis using MLPG method.

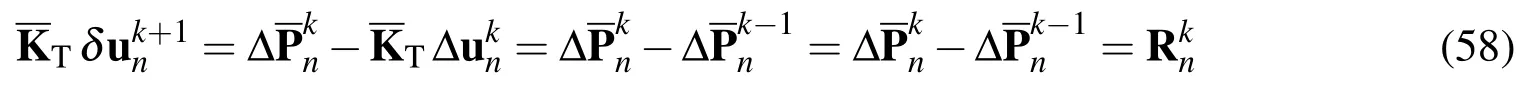
At the first iteration one can writes:

5 Numerical examples and discussions

In this section,the governing equations are analytically solved for nonlinear analysis of 2D hyper-elastic domains to show the capability of the MLPG method.

5.1 Verification of the present method:Nonlinear static analysis of cantilever deep beam

In the first example,a cantilever deep beam subjected to uniformly distributed shear stress at the free end of the beam is analyzed and the present results are compared with those of Gu,Wang,and Lam(2007).The thickness and the length of the deep beam are 2mand 10m,respectively.In this example,the beam is considered to be made of hyper-elastic neo-Hookean material with Lame constantsµ=5×103Pa,λ=3.3×103Pa.The following boundary conditions are assumed for the problem:

where at thekth loading step,the uniformly distributed shear stress‘fk’is:

where ‘β’is load scaling factor which is equal to ‘β =10’.In table 1 the vertical displacement of point‘A’(see Fig.4)obtained by the MLPG method with various nodal distribution are compared with those obtained by LoKriging method[Gu,Wang,and Lam(2007)].As can be seen in this table,in node distribution(6×11)a good agreement with the LoKriging solution is achieved.

Table 1:Vertical displacement of node A.

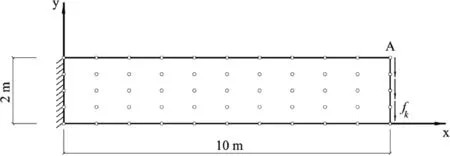
Figure 4:A sketch of cantilever deep beam subjected to shear force and nodal distribution.

In Fig.5 the vertical displacement along the top surface of the beam(y=h)for loading steps‘N=2’,‘N=4’,‘N=6’,and ‘N=8’are plotted and compared with the FEM results[Gu,Wang,and Lam(2007)].The percentage of differences in all points in this figure is less than 3 percent.This figure demonstrates the accuracy of the MLPG method for very large deformation problems.

5.2 FGM cantilever deep beam under shock loading

After verifying the results,the aforementioned beam is analyzed under the mechanical shock loading.The beam is supposed to be made of continuous combination of two distinct kinds of materials ‘M1’and ‘M2’.So that,the bottom and the top surfaces of the beam are entirely made of materials‘M1’and ‘M2’,respectively and the material properties at an arbitrary point of beam can be obtained as follows.

where ‘n’is non-negative volume fraction exponent,‘E’is elasticity modulus and‘ρ’is mass density of material.The mechanical properties of materials ‘M1’and‘M2’are listed in Table 2.

Table 2:Basic constituents of FGM.

The first five linear natural periods of vibration of the beam for various volume fraction exponents are listed in Table 3.As would be expected,the natural periods is decreased by increasing the volume fraction exponent.

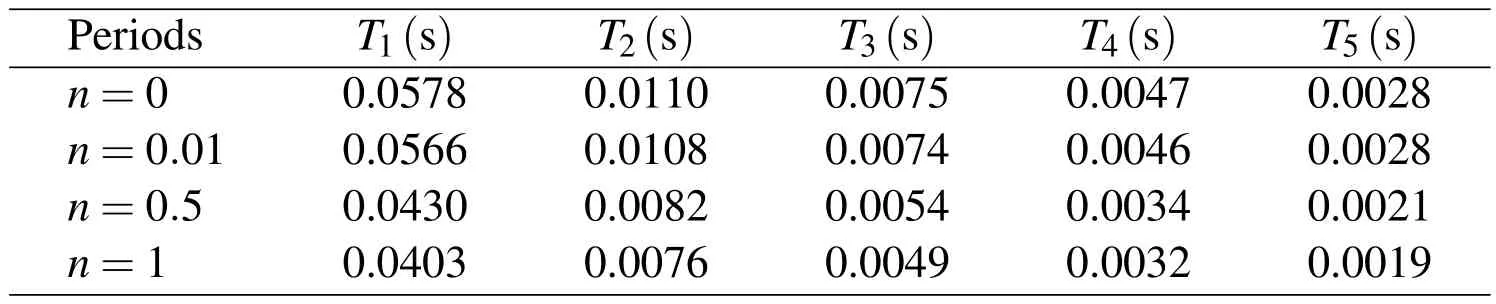
Table 3:Effect of volume fraction exponent on linear periods.

The same boundary conditions introduced in previous example(Eqs.(61)to(64))are considered with the following uniformly distributed time dependent shear stress‘fk’.

where ‘P0=18e8Pa/s’.Fig.6 shows the time history of the vertical displacement at the point‘A’obtained from nonlinear analysis with neo-Hookean constitutive model for‘n=0’and ‘ξ =0’.The obtained results from linear analysis are also plotted in the same figure.As can be seen in Fig.6,the vertical displacement amplitude of point‘A’in nonlinear analysis is smaller than the linear result.It means that the nonlinear analysis makes the beam stiffer than the linear analysis.

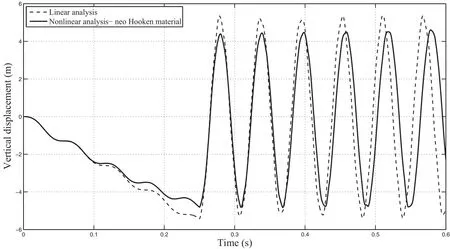
Figure 6:The comparison between linear and nonlinear time histories of vertical displacement of point‘A’for‘n=0’and ‘ξ =0.

Fig.7 shows the time history of vertical displacement at the point‘A’for‘ξ =0’.This figure is plotted with different values of volume fraction exponent.Increasing in the frequency and decreasing in the amplitude of vibration with increasing in volume fraction exponent‘n’is obvious in this figure.According to this figure it can also be seen that the period of free vibration is almost the same fundamental(first)natural period of the system presented in table.3.

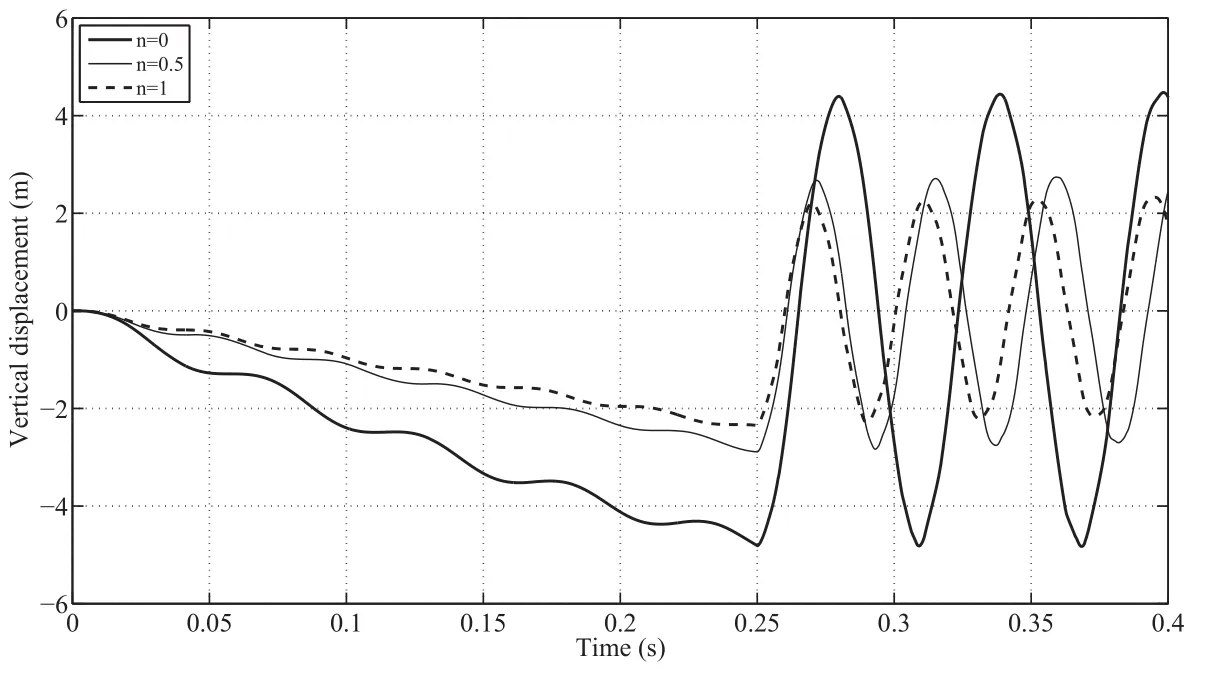
Figure 7:Effect of material grading pattern on time history of vertical displacement.

Fig.8 shows the effects of damping ratio ‘ξ’on time history of vertical displacement for ‘n=0’.This figure shows that,in typical range of damping ratios,the damping does not have significant influence on value of maximum vertical displacement and frequency of vibration.Also,it can be found that by increasing the damping ratio the rate of vibration decays will be increased.

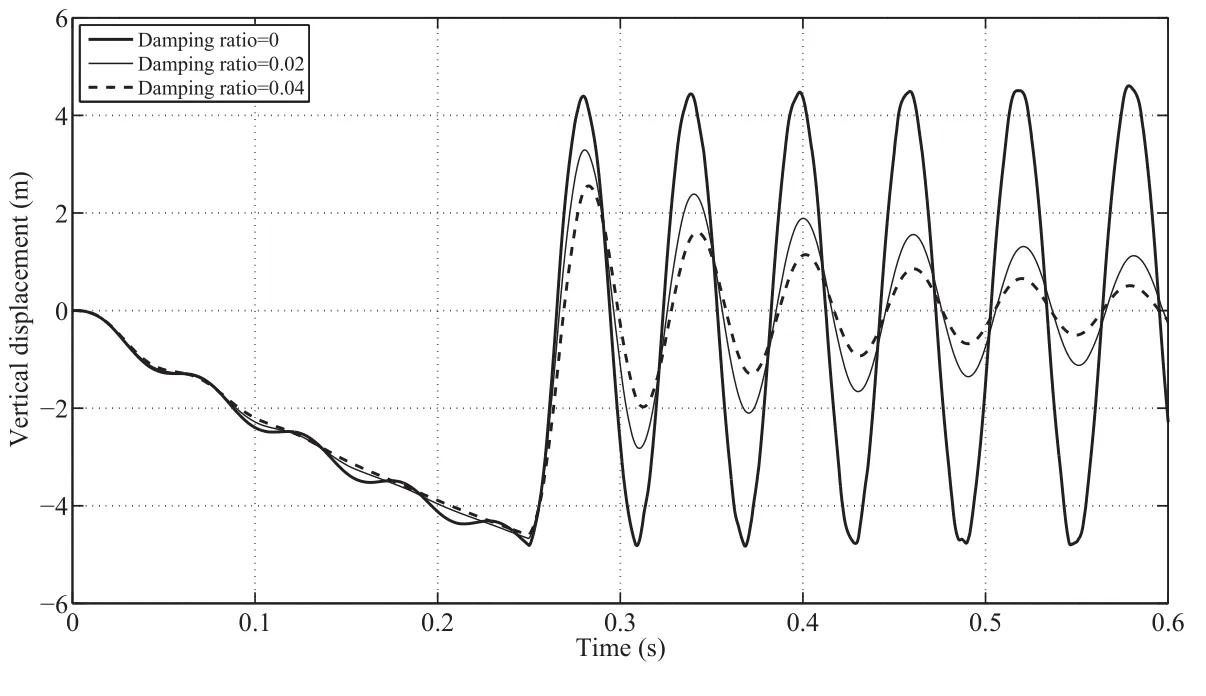
Figure 8:Effect of damping ratio on time history of vertical displacement.

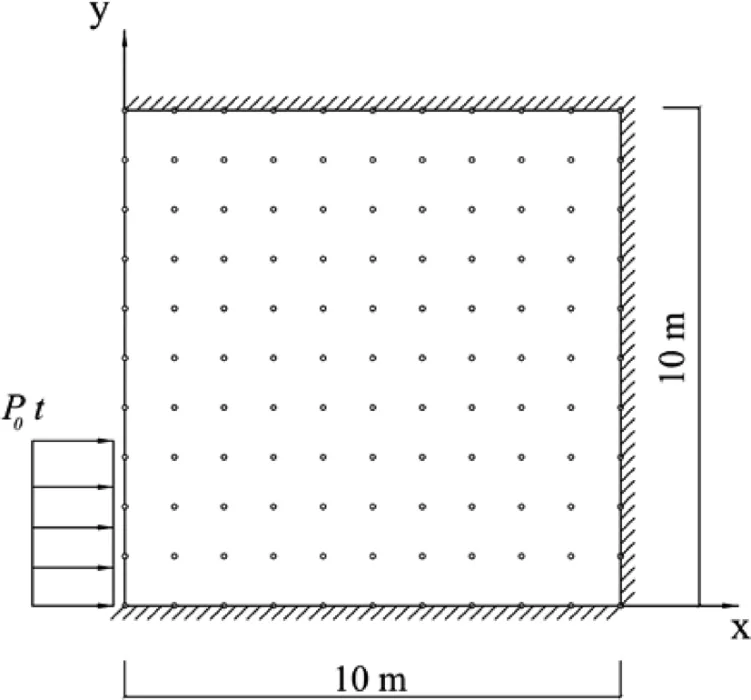
Figure 9:Two dimensional domain:geometry and boundary conditions.

5.3 Nonlinear wave propagation in two dimensional domains

In this section,the nonlinear horizontal displacement wave propagation of the two dimensional domain(5m×5m)with the following boundary conditions is studied(see Fig.9).

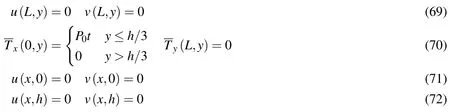
It is assumed that‘P0=8e12Pa/s’.The material properties are simulated using the rule of mixture as follows:

The wave propagation of horizontal displacement obtained by linear and nonlinear analysis can be tracked in Figs.10a and 10b,respectively.Comparing these figures reveals that there is no any significant difference between linear and nonlinear wave propagation speed.

Figure 10:Linear and nonlinear 2D wave propagation of horizontal displacement for‘n=0’and ‘ξ =0’.(a)Linear analysis(b)Nonlinear analysis.

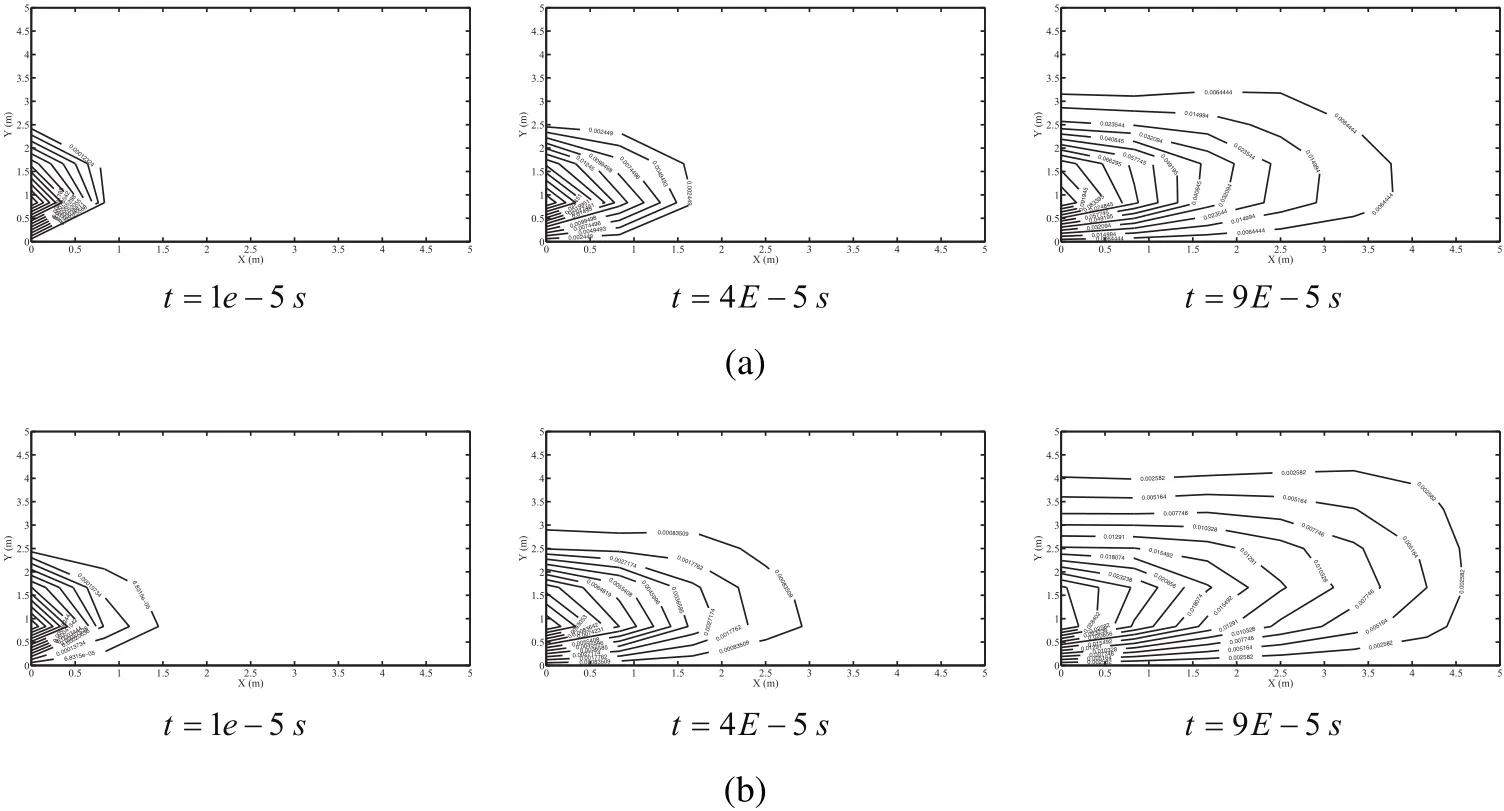
Figure 11:The 2D wave propagation of horizontal displacement for‘ξ =0’and various volume fractions.(a)‘n=0.01’(b)‘n=1’.

Fig.11 depicts the 2D horizontal displacement wave propagation for a FG domain with various grading patterns through horizontal direction.As would be expected,the grading pattern has significant effect on wave propagation so that by increasing the value of volume fraction exponent,the wave propagation speed is increased but the values of horizontal displacement contours are decreased.

The influence of damping ratio on nonlinear wave propagation is studied in Fig.12.

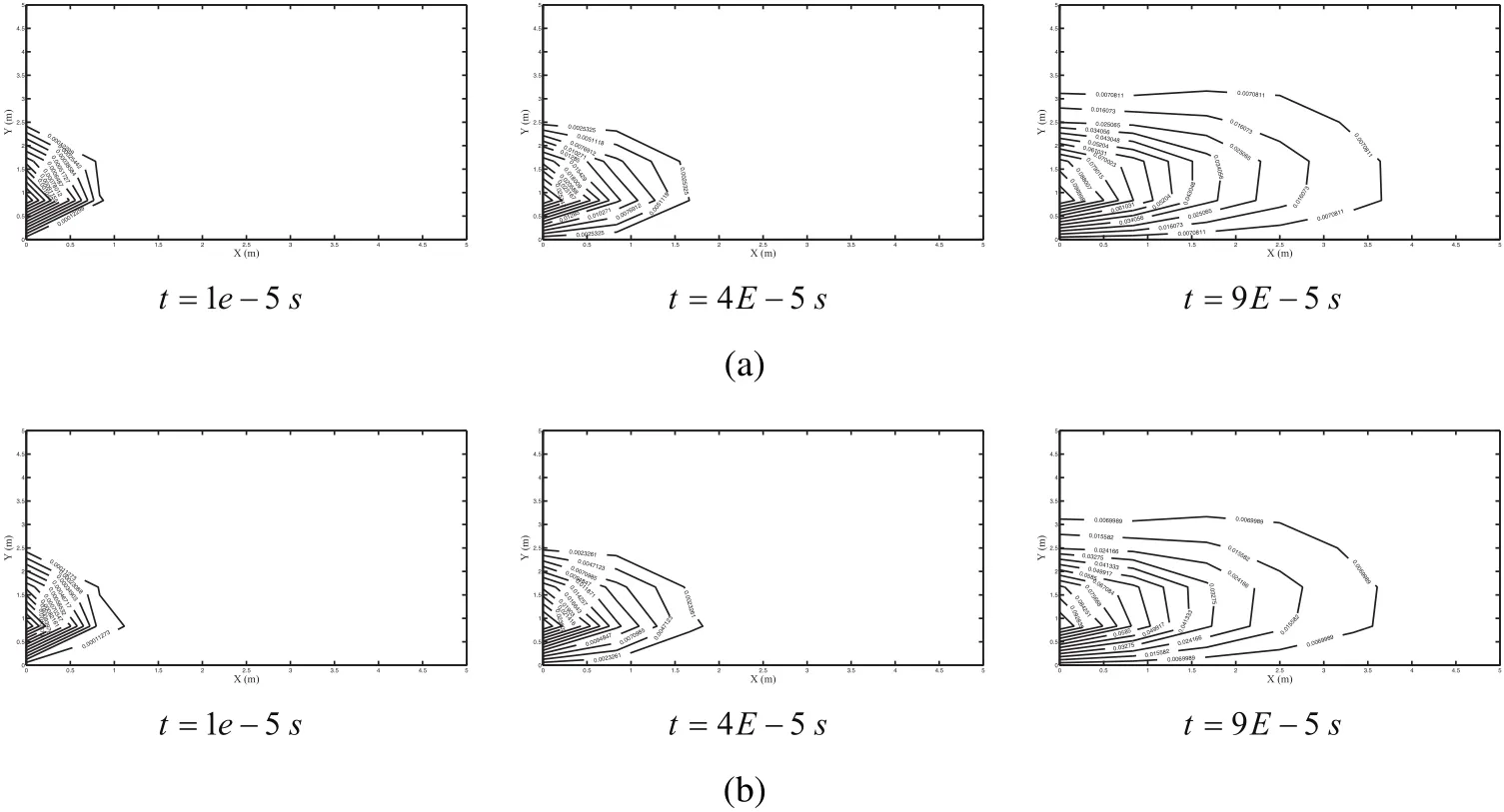
Figure 12:The 2D wave propagation of horizontal displacement for ‘n=0’and various damping ratios.(a)‘ξ =0.02’(b)‘ξ=0.08’.

It can be seen that by increasing the value of damping ratio,the wave propagation speed is identical but the values of radial displacement contours are decreased.It should be mentioned that the effect of the damping ratio on wave propagation is not very significant.

6 Conclusions

In this paper,the MLPG method is applied to study the time history and nonlinear wavepropagationin2Ddomains.Consideringthelargedeformations,itisassumed that the domain be made of large deformable neo-Hookean materials.The mechanical properties of FG domain are simulated using volume fractions exponent.The domain is analyzed under mechanical shock loading applied on its bounding surfaces.Rayleigh damping is employed to model energy dissipation in analyses.To obtain the solution of nonlinear equation of motion in time domain,the MLPG method is combined with the Newmark/Newton-Raphson technique with suitable time steps.Several numerical examples are given to demonstrate the accuracy and effectiveness of the presented method for two-dimension large deformation problems.The brief outline of the paper is as follows:

•Numerical examples demonstrate the accuracy and effectivenessof presented MLPG method for large deformation problems.

•A comparison between the time histories of linear and nonlinear analyses of cantilever deep beam under mechanical shock loading applied at the free end,shows that the nonlinear analysis makes the beam stiffer compared with the linear analysis.

•The volume fraction exponent increasing causes the decreasing of the amplitude of vibration and the increasing of the frequency of vibration.

•By increasing the damping ratio,the rate of vibration decays is increased.The damping does not have significant influence on value of maximum vertical displacement and frequency of vibration.

•The obtained results from linear and nonlinear analysis in 2D rectangular domain show that there is no any significant difference between linear and nonlinear results.It means that the obtained results from linear analysis can be employed for 2D wave propagation assessment.

•By increasing the value of volume fraction exponent,the wave propagation speed is increased and the values of radial displacement contours are decreased.

•By increasing the value of damping ratio,the wave propagation speed is almost identical and the values of horizontal displacement contours are slightly decreased.

Atluri,S.N.;Sladek,J.;Sladek,V.;Zhu,T.(2000):The local boundary integral equation(LBIE)and its meshless implementation for linear elasticity.Computational Mechanics,vol.25,pp.180–198.

Atluri,S.N.;Zhu,T.(1998):A new meshless local Petrov-Galerkin(MLPG)approachincomputationalmechanics.ComputationalMechanics,vol.22,pp.117–127.

Belytschko,T.;Lu,Y.Y.;Gu,L.(1994):Element free Galerkin methods.International Journal for Numerical Methods in Engineering,vol.37,pp.229–256.

Cai,Y.C.;Zhu,H.H.(2004):A meshless local natural neighbour interpolation method for stress analysis of solids.Engineering Analysis with Boundary Elements,vol.28,pp.607–613.

Chen,S.S.;Xu,C.J.;Tong,G.S.(2015):A meshless local natural neighbour interpolation method to modeling of functionally graded viscoelastic materials.Engineering Analysis with Boundary Elements,vol.52,pp.92–98.

Chopra,A.K.(2001):Dynamics of structures:Theory and applications to earthquake engineering.Prentice Hall:New Jersey.

Ghadiri Rad,M.H.;Shahabian,F.;Hosseini,S.M.(2015): Geometrically nonlinear elastodynamic analysis of Hyper-Elastic Neo-Hookean FG cylinder subjected to shock loading using MLPG method.Engineering Analysis with Boundary Elements,vol.50,pp.83–96.

Ghadiri Rad,M.H.;Shahabian,F.;Hosseini,S.M.(2015):A meshless local Petrov-Galerkin method for nonlinear dynamic analyses of hyper-elastic FG thick hollow cylinder with Rayleigh damping.Acta Mechanica,vol.226,pp.1497–1513.Gingold,R.A.;Monaghan,J.J.(1977): Smoothed particle hydrodynamics:theory and application to non-spherical stars.Monthly Notices of the Royal Astronomical Society,vol.181,pp.375–389.

Gu,Y.T.;Wang,Q.X.;Lam,K.Y.(2007):A meshless local Kriging method for large deformation.Computer Methods in Applied Mechanics and Engineering analyses,vol.196,pp.1673–1684.

Hehua,Z.;Wenjun,L.;Yongchang,C.;Yuanbin,M.(2007):A meshless local natural neighbor interpolation method for two-dimension incompressible large deformation analysis.Engineering Analysis with Boundary Elements,vol.31,pp.856–862.

Hosseini,S.M.;Shahabian,F.;Sladek,J.;Sladek,V.(2011):Stochastic meshless local Petrov-Galerkin(MLPG)method for thermo-elastic wave propagation analysis in functionally graded thick hollow cylinders.CMES:Computer Modeling in Engineering&Sciences,vol.71,no.1,pp.39–66.

Hosseini,S.M.;Sladek,J.;Sladek,V.(2011):Meshless local Petrov-Galerkin method for coupled thermoelasticity analysis of a functionally graded thick hollow cylinder.Engineering Analysis with Boundary Elements,vol.35,pp.827–835.

Hosseini,S.M.;Sladek,J.;Sladek,V.(2013): Application of meshless Local Integral Equations to two dimensional analysis of coupled non-Fick diffusionelasticity.Engineering Analysis with Boundary Elements,vol.37,pp.603–615.

Hosseini,S.M.;Sladek,J.;Sladek,V.(2014):Two dimensional transient analysis of coupled non-Fick diffusion-thermoelasticity based on Green-Naghdi theory using meshless local Petrov-Galerkin(MLPG)method.International Journal of Mechanical Sciences,vol.82,pp.74–80.

Lin,J.;Naceur,H.;Coutellier,D.;Laksimi,A.(2014): Efficient meshless SPH method for the numerical modeling of thick shell structures undergoing large deformations.International Journal of Non-Linear Mechanics,vol.65,pp.1–13.

Liu,G.R.;Gu,Y.T.(2005):An Introduction to Meshfree Methods and Their Programming.Springer.

Liu,W.K.;Jun,S.;Li,S.;Adee,J.;Belytschko,T.(1995):Reproducing kernel particle methods for structural dynamics.International Journal for Numerical Methods in Engineering,vol.38,pp.1655–1679.

Moussavinezhad,S.M.;Shahabian,F.;Hosseini,S.M.(2013):Two dimensional stress wave propagation in finite length FG cylinders with two directional nonlinear grading patterns using MLPG method.Journal of Engineering Mechanics,vol.140,pp.575–592.

Sladek,J.;Sladek,V.;Krivacek,J.;Wen,P.H.;Zhang,C.H.(2007):Meshless local Petrov-Galerkin(MLPG)method for Reissner-Mindlin plates under dynamic load.Computer Methods in Applied Mechanics and Engineering,vol.196,pp.2681–2691.

Sladek,J.;Sladek,V.;Zhang,C.H.;Schanz,M.(2006): Meshless local Petrov-Galerkin method for continuously nonhomogeneous linear viscoelastic solids.Computational Mechanics,vol.37,pp.279–289.

Sladek,J.;Stanak,P.;Han,Z.D.;Sladek,V.;Atluri,S.N.(2013):Applications of the MLPG method in engineering&sciences:A review.CMES:Computer Modeling in Engineering&Sciences,vol.47,no.1,pp.61–96.

1Civil Engineering Department,Faculty of Engineering,Ferdowsi University of Mashhad,Mashhad,Iran

2Corresponding author:Farzad Shahabian,Tel:+98 513 38805047,Fax:+98 513 38763301,E-mails:fshahabianm@yahoo.com&shahabf@um.ac.ir

3Industrial Engineering Department,Faculty of Engineering,Ferdowsi University of Mashhad,Mashhad,Iran