物流配送车辆调度路径优化问题算法研究

浮萍萍，叶春明，李佳桐

FU Ping-ping, YE Chun-ming, LI Jia-tong

（上海理工大学 管理学院，上海200093）

(Management School, University of Shanghai for Science and Technology, Shanghai 200093, China)

0 引 言

由国家发展和改革委员会、国家统计局和中国物流与采购联合会2014 年3 月7 日联合发布的《2013 年全国物流运行情况通报》[1]显示，2013 年中国社会物流总费用10.2 万亿元，同比增长9.3%，与GDP 的比率为18%。这一比率远高于美国的8.5%，日本的8.7%和德国的8.3%，高于全球平均水平约6.5 个百分点。这些数据反映出中国物流成本偏高的现状。物流总费用中运输费用5.4 万亿元，同比增长9.2%，占社会物流总费用的比重为52.5%。同时，2013 年中国物流业增加值3.9 万亿元，同比增长8.5%。可以看出，全社会物流企业收入增速低于物流费用增速，物流企业普遍盈利能力偏低。报告总结性的指出，2013 年，我国物流运行总体平稳，物流需求规模保持较高增幅，物流业增加值平稳增长，但经济运行中的物流成本依然较高。

随着人们对环境问题给予越来越多的关注，关于要求企业保护环境的法律条文相继增加。其中，减少废物的排放量和能源的消耗成为法律规定的两个重要内容。物流作为一个与环境关系密切的行业，车辆调度配送路径优化问题同时涉及能源消耗和废物的排放问题，因而其一直是国内外研究的热点。

综上所述，作为继原材料、劳动力以外的“第三利润源泉”，实现物流合理化具有重要的经济意义与现实意义。一方面，物流配送车辆路径优化有助于企业降低物流成本，提高运作效率，从而增加企业利润。另一方面，通过缓解交通压力，减少资源消耗和对环境的污染真正做到环保物流。

1 车辆调度问题描述

物流配送车辆路径优化问题最早是由线性规划之父Dantzig 和Ramser[2]在1959 年提出，该问题是交通运输管理、智能救灾调度指挥系统、网络作业调度管理系统、现代物流系统、物流网等应用、研究领域中的基本问题之一，也是最重要的调度问题之一。

配送车辆调度问题要解决的问题[3]是车辆从配送中心（这里的配送中心是个广义概念，指的是车辆的出发地，包括物流中心、配送中心、仓库、车场等） 出发去完成一些配送任务，当各任务量较小（小于车辆容量） 时，为了提高车辆的利用率，可安排一辆车执行几项运输任务。这时，如何安排车辆的路线，使得既满足各任务的需求并完成任务，而又使总成本最小（这里的总成本指的是一个广义概念，包括时间最少、运营费用最少等） 涉及的就是配送车辆路径优化问题。

在学术研究方面一般把这个问题抽象解释为路线安排问题或者车辆路径问题（Vehicle Routing Problem，VRP），可描述如下：有一个或几个配送中心Di（i=1,2,…,n），每个配送中心有K种不同的车型，每种车型有n量车。有一批配送业务Ri（i=1,2,…,n），已知每个配送业务的需求量qi（i=1,2,…,n），要求在一定的时间范围内[Ei,Li]完成，求在满足不超过配送车辆载重量等的约束条件下，安排配送车辆在合适的时间及最优路线等约束条件下总成本最小。

2 VRP 的构成要素分析

配送车辆调度问题主要包括道路、货物、车辆、物流中心、客户、运输网络、约束条件和目标函数等要素。VRP 问题主要是以下几个因素的多个组合[4]：（1） 道路。道路是货物运输的基础，也是构成VRP 的核心要素之一。通常用从中心仓库出发按照一定的路线依次经过各个客户点，最后返回配送中心所形成的网络图表示。（2） 货物。货物是配送的对象，包括品名、包装、重量、体积、要求送到（或取走） 的时间和地点、能否分批配送等属性。（3） 车辆。车辆是货物的运载工具。其主要属性包括车辆的类型、转载量、一次配送的最大行驶距离、配送前的停放位置及完成任务的停放位置等。（4） 物流中心。也称为物流基地、物流据点，是指进行集货、分货、配货、送货作业的配送中心、仓库、车站、港口等。（5） 客户。也称为用户，包括分仓库、零售商店等。客户的属性包括需求（或供应） 货物的数量、需求（或供应） 货物的时间、需求（或供应） 货物的次数及需求（或供应） 货物的满足程度等。（6） 运输网络。运输网络由顶点（指物流中心、客户、停车场）、无向边和有向弧组成。边、弧的属性包括方向、权值和交通流量限制等。（7） 约束条件。配送车辆调度问题应满足的约束条件主要包括：①在允许通行的时间进行配送。②在物流中心现有运行能力范围内等。③满足客户对货物发到时间范围的要求。④满足所有客户对货物品种、规格、数量的要求。⑤车辆在配送过程中的实际载货量不得超过车辆的最大允许装载量。（8） 目标函数。配送车辆调度问题可以只选用一个目标，也可以选用多个目标。经常选用的目标函数主要有：①最大化准时性。②最小化劳动消耗。③最大化运力利用。④最小化综合费用。⑤最小化配送总里程。⑥最小化配送车辆的吨位公里数。

由以上各要素组成的VRP 简单示意图如图1 所示：

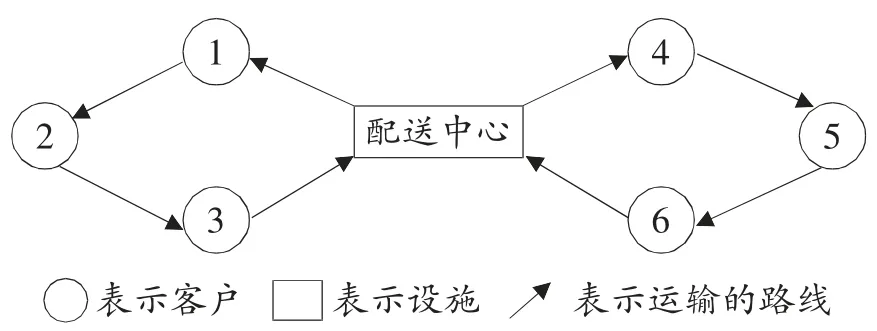
图1 VRP 示意图

3 VRP 的分类

根据研究重点的不同，VRP 存在多种分类方式[5]：（1） 按照需求是否可切分，可以分为可切分的VRP 和不可切分的VRP；（2） 按照每个顾客需求量是否超过车的容量，可以分为满载车辆路径问题和非满载车辆路径问题；（3） 按照约束条件的不同可以分为带有容量限制的车辆路径问题（CVRP）、带时间距离约束的车辆路径问题（DVRP） 以及带有时间窗的车辆路径问题（VRPTW） 等；（4） 按照已知信息的特征可以分为确定性VRP 和不确定性VRP。其中不确定性VRP 可进一步分为随机车辆路径问题（SVRP） 和模糊车辆路径问题（FVRP）；（5） 按照配送中心的数量可以分为单车场车辆路径问题（SVRP），即一般车辆路径问题（VRP），以及多车场车辆路径问题（MVRP），其中MVRP 可以根据是否每辆车都有固定的终点车场分为终点车场固定的MVRP 和终点车场不固定的MVRP。

4 VRP 的基础理论

4.1 线性规划理论。线性规划（Linear Programming） 是一种在科学与工程领域广泛应用的数学模型。作为运筹学的一个基本分支，线性规划是实现管理现代化的有力工具。线性规划问题研究的是一个线性函数在一组线性等式或不等式组成的约束条件下的极值。主要分为两类：（1） 对于一项确定的任务进行统筹安排，达到在使用最少的人力物力资源的情况下完成这一任务的目标。（2） 对确定数量的人力物力资源，通过合理安排使用达到完成任务最多的目标。

线性规划问题的共同特征为：（1） 每一个问题都是求一组变量（称为决策变量） 的值。这组变量的每一组定值分别代表一个具体方案。通常这组变量的取值是非负的。（2） 存在一定的限制条件，称为约束条件。这些约束条件都可以用一组线性等式或不等式来表示。（3） 都有一个期望达到的目标，并且这个目标可以表示为决策变量的线性函数（称为目标函数）。按照所研究问题的不同，要求目标函数值最大化（max） 或者最小化（min）。

由共同特征可以得出线性规划问题模型的一般形式为[6]：（1） 决策变量目标函数：max （minz）约束条件其中，“max（min）”是“maximize（minimize）”的缩写，含义为“最大化（最小化）”。

4.2 组合优化理论。组合优化（Combinatorial Optimization），又称离散优化，是运筹学的一个经典分支。它研究的是在离散的、有限的数学结构即问题的可行解集中，求满足约束条件的目标函数最大化（max） 或最小化（min）。

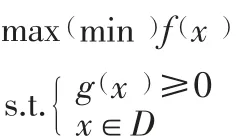
组合优化问题的数学模型可描述为：其中，f（x）为目标函数，g（x）为约束函数，x为决策变量，D表示有限个点组成的集合。一个组合优化问题可以简单地表示为三个参数（D,F,f）。其中D为决策变量定义域，F为可行解区域，满足F=｛x|x∈D,g（x）≥0 ｝，F中的任何一个元素称为该组合优化问题的可行解，f为目标函数，满足的可行解称为该组合优化问题的最优解[7]。组合优化的特点是可行解集合为有限点集，且有可行解一定有最优解。由直观可知，只要将D中的有限个点逐一判别是否满足条件函数g（x）的约束和比较各自所对应的目标值f（x）的大小，即可得到该问题的最优解。在现实生活中，大量优化问题就是从有限个状态中选取最好的一个，因而属于组合优化问题。

4.3 运输问题。运输问题（Transportation Problem） 是一类具有特殊结构的组合优化问题。其具体数学描述为：某种产品有m个产地A1,A2,…,Am，产量分别为a1,a2,…,am，有n个销售地B1,B2,…,Bn销售该产品，销量分别为b1,b2,…,bn，从产地Ai（i=1,2,…,m）调到销售地Bj（j=1,2,…,n）的调运量为xij，单位产品运价为yij。假定产销平衡，即总产量等于总销量，则有求如何确定运输方案，使得调运产品的总运费最小[8]？该问题的数学模型为：求xij，使得：

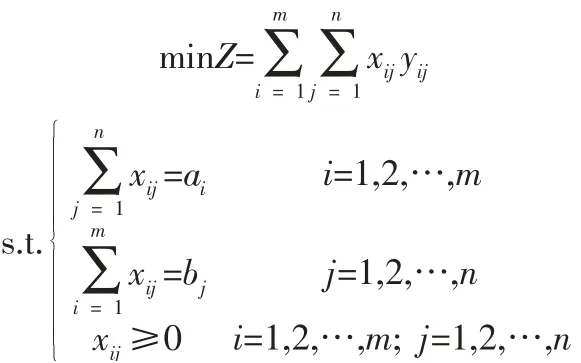
5 VRP 的优化算法

车辆运输调度问题的求解算法有很多种，但究其本质来讲，基本可分为最优化算法（Exact Algorithm） 和启发式算法（Heuristic Algorithm）[9]。

5.1 最优化算法。最优化算法，也称为精确算法，是指能够通过有限的严谨计算和推理，运用整数规划、线性规划和非线性规划等数学规划技术或数据结构得到优化问题的最优解的算法。在物流车辆运输调度问题中，所谓最优化算法就是找到一组路径集合，使得其目标函数值比其它任何一组可行路径集合的目标函数值更好。

对于精确算法，Desrochers[10]，Kohland Madsen[11]，Fisher[12]等人做过相关的研究，其中又可以分为分支定界法（Branch-andbound）、动态规划法（Dynamic Programming）、切平面法（Cutting Planes） 等。精确算法可以求得模型的精确解，但是它只能解决规模比较小的问题，即配送车辆数和客户数都比较少的问题。通常情况下，由于车辆路径优化问题是NP 难题，问题规模较大，导致计算量会呈现组合爆炸（Combination Explosion） 的现象。同时，求解时间也呈指数函数的增长趋势。由于这两方面的限制，在解决实际问题中精确算法的应用范围有限，因此相应的研究也越来越少。

5.2 启发式算法。启发式算法是相对于最优化算法提出的，指通过对过去经验的归纳推理及实验分析来解决问题的方法，即基于直观推断或经验构造的算法。因此，启发式算法要求分析人员运用自己的感知和洞察力，从与研究问题有关且比较具体的模型及算法中寻求相互间的联系，从中得到启发，发现适合于解决该问题的思路和途径。

使用启发式算法求解问题时强调主体对所求解的“满意度”，即常常是得到满意解，而不去追求最优解。之所以这样是因为：（1） 很多问题不存在严格的最优解，此时对目标的满意性比最优性更能描述所需的选择行为。（2） 得到某些问题最优解的成本太大。（3） 从实际出发，有时探求问题的最优解没有实际意义。

启发式算法指根据某种启发式的信息对已知的可行解进行改善，通过若干次的迭代获得相对满意的解。与精确算法相比，启发式算法得到的解不一定是最优解，但很有可能是近似解。同时，启发式算法实现起来相对简单，并且可以在相对短的时间内快速地找到满意解。为此研究人员主要把精力放在构造高质量的启发式算法上。目前专家已提出很多求解车辆运输调度问题的启发式算法，主要分为经典启发式算法和现代启发式算法两类。

车辆路径的启发式算法最早由Clarke 和Wright 提出的用于解决车辆数不固定的节约法（The Savings Method）[13]，Gillett 和Miller 提出的先分群再安排路线的扫描法（Sweep Method）[14]，Bramel 和Simchi-Levi 提出的基于选址问题转化的LBH 算法[15]，Cullew，Jarvis 和Ratliff 提出的两段法[16]，Fisher 和Jaikumar 建立的先分组后安排路线的一般分配算法[17]，Christofides 和Minggozzi 等建立的不完全树搜索算法[18]，Pureza 和Franca 研究的禁忌搜索算法（Tabu Research，TS）[19]等。这些算法为求解车辆路径问题提供了有效的方法，但也存在着一系列问题。如节约法可以列出各点对时间的节约量，并按节约量从大到小构造路径，因此具有运算速度快的优点，但存在未组合点零乱、边缘点难于组合的缺点；扫描法属于非渐近优化；LBH 算法则存在问题转化麻烦且选址问题本身难解等。

针对车辆路径问题的特点，构造运算简单、寻优性能优异的启发式算法，这不仅对于配送系统而且对于许多可转化为车辆路径问题求解的优化组合问题具有十分重要的意义。很多学者运用新的算法来求解车辆调度问题，如：由N. Metropolis 等人于1953 年提出的模拟退火算法（Simulated Annealing Algorithm，SA）[20]、由美国Michigan 大学J.Holland 教授于1975 年提出的遗传算法（Genetic Algorithm，GA）[21]、由M. Dorigo 等人于1991 年提出的蚁群算法（Ant Colony Optimization，ACO）[22]、由Kennedy 和Eberhart 于1995 年提出的粒子群算法（Particle Swarm Optimization，PSO）[23]、由剑桥大学的杨新社教授（Xin-She Yang） 提出的萤火虫算法（Firefly Algorithm，FA）[24]等优化方法。

6 结束语

关于物流配送车辆优化调度研究的算法已广泛应用于生产和生活的各个方面，并已经取得了良好的经济效益。随着我国国民经济健康稳步地向前发展，尤其是在电子商务发展迅速的大背景下，现代物流业发展十分迅速，这些都对以运输为中心的物流配送活动提出了更高的要求。如何针对各种地形的条件和各行业物流配送运输的特点，结合不同的启发式算法进行优势互补和消除缺陷，设计出通用性好、运算速度快、精度高的优良算法，这将是今后研究发展的方向。

[1] 国家统计局. 2013 年全国物流运行情况通报[EB/OL]. (2014-03-06)[2014-11-20]. http://www.stats.gov.cn/tjsj/zxfb/201403/t20140306_520357.html.

[2] Dantzig G, Ramser J. The Truck Dispatching Problem[J]. Management Science, 1959,6(1):80-91.

[3] 李军，郭耀煌. 物流配送车辆优化调度理论与方法[M]. 北京：中国物资出版社，2001.

[4] 陈震. VPN 技术及其应用的研究[J]. 电脑知识与技术，2009(4):798-799.

[5] 占书芳. 并行遗传算法在带软时间窗车辆路径问题中的应用研究[D]. 武汉：武汉理工大学（硕士学位论文），2006.

[6] 刘宝碇，赵瑞清，王纲. 不确定规划及应用[M]. 北京：清华大学出版社，2003.

[7] 郎茂祥. 配送车辆优化调度模型与算法[M]. 北京：电子工业出版社，2009.

[8] 刘东圆. 运输能力限制下的运输问题研究[D]. 北京：北京交通大学（硕士学位论文），2009.

[9] Sung-Chul Hong, Yang-Byung Park. A Heuristic for Constraints[J]. International Journal of Production Economics, 1999,62:249-258.

[10] Desrocher M., Desroslers J., Solomom M.. A New Optimization Algorithm for the Vehicle Routing Problem with Time Windows[J]. Operations Research, 1992,40:342-354.

[11] Kohl N., Madsen O.. An Optimization Algorithm for the Vehicle Routing Problem with Time Windows Based on Lagrangean Relocation[J]. Operations Research, 1997,45:395-406.

[12] Fisher M., Jornsten K., Madsen O.. Vehicle Routing with Time Windows: Two Optimization Algorithms[J]. Operations Research, 1997,45:488-492.

[13] Clarke G., Wright J.. Scheduling of Vehicles from a Central Depot to Number of Delivery Points[J]. Operations Research,1964,12(4):12-18.

[14] Gillitt B. E., Millier L. R.. A Heuristic Algorithm for the Vehicle Dispatch Problem[J]. Operations Research, 1974,22:340-349.

[15] Bramel J., Simchi-Levl D.. A Location Based Heuristic for General Routing Problems[J]. Operations Research, 1995,43:649-660.

[16] Desrochers M, Lcustra J. K., Savelsbergh M. W.. A Classification Scheme for Vehicle Routing and Scheduling Problems[J].European Journal of Operational Research, 1990,46(3):322-332.

[17] Fisher M. L., Jaikumar R.. A Generalized Assignment Heuristic for Vehicle Routing[J]. Networks, 1981,11:109-124.

[18] Christofides N., Minggozzi A., Toth P.. The Vehicle Routing Problem[M]. Combinatorial Optimization. Chechester: Wiley,1979:315-338.

[19] Pureza V. M., Franca P. M.. Vehicle Routing Problems Via Tabu Search Metaheuristics[R]. Technical Report CRT-747,Centre de Recherchesurles Transports, Montreal, 1991.

[20] Metropolis N, Rosenbluth A, Rosenbluth M, et al. Equation of State Calculations by Fast Computing Machines[J]. Journal of Chemical Physics, 1953(21):1087-1092.

[21] Holland J. H. Adaptation in Natural and Artificial System[M]. Cambridge. Massachusetts: MIT Press, 1975.

[22] Colorni A, Dorigo M, Maniezzo V, et al. Distributed Optimization by Ant Colonies[C] // Proceedings of European Conference on Artificial Life, Paris, 1991:134-142.

[23] Kennedy J, Eberhart R. Particle Swarm Optimization[C]//Proceedings of IEEE International Conference on Neural Networks,1995:1942-1948.

[24] Yang Xin-she. Nature-inspired Metaheuristic Algorithms[M]. Luniver Press, UK. 2008.