水流作用下填埋场开裂黏土衬垫数值仿真计算

董祎挈，陆海军，戴　睿，何　丽

(1.武汉轻工大学 多孔介质力学研究所，湖北 武汉 430023；2.江汉大学文理学院 机电与建筑工程学部，湖北 武汉 430056)



水流作用下填埋场开裂黏土衬垫数值仿真计算

董祎挈1，陆海军1，戴睿1，何丽2

(1.武汉轻工大学 多孔介质力学研究所，湖北 武汉 430023；2.江汉大学文理学院 机电与建筑工程学部，湖北 武汉 430056)

摘要：针对垃圾填埋场压实黏土封场系统在干旱与半干旱地区出现的干燥开裂的问题，基于流体动力学流动方程，建立了多孔介质不连续裂缝中水流流动数学模型，采用COMSOL模拟开裂黏土水渗流规律。数值模拟计算结果表明，流体的压强所出现的最大值和最小值分别出现在入口和出口的边缘处，流体在裂缝中流速较大的区域主要分布在水流的入口和出口处的边缘，越靠近裂缝的两端，裂缝中的流体的运动状态与基质中的流动状态差异性越大。

关键词：数值仿真；压实黏土；干燥开裂

1引言

压实黏土封场系统即填埋场顶部隔断层，由1m厚压实黏土层、1mm厚的HDPE防渗膜和400 g/m2的无纺布复合构成，用来阻挡地表降水渗入废物层，以减少渗沥液的渗出量。在自然降雨入渗条件下封场系统的开裂是威胁填埋场运行安全的重要因素之一。封场系统内的水体流动易致使压实黏土层渗透系数、水导热系数等物性参数变化，进而改变封场系统的水分迁移和土体变形等特性，最终影响封场系统的开裂[1-3]。

水流流动是造成压实黏土开裂的原因之一，水流在压实黏土裂缝和孔隙中流动过程中所引起黏土颗粒表面摩擦系数、颗粒所受压力等物性参数的变化对黏土的抗压、抗剪强度等工程特性造成一定的影响，进而影响压实黏土中的应力场与位移的变化，最终导致压实黏土封场系统的开裂[4-6]。由于流体在多孔介质中流动会受到孔隙壁摩擦力的影响，流体的流速会变得非常小，故一般会采用达西渗流模型来模拟流体通过多孔介质间隙的流动[7]。这种模型也被广泛应用于模拟水流在蓄水层和河岸里的迁移过程、油井中石油的迁移过程以及地底岩浆向火山口的迁移过程等。

国内外科学工作者[8-9]大多是通过干湿循环试验对填埋场黏土开裂情况进行宏观观测，或采用离散元模拟了土壤干燥收缩及开裂特性[10]，而水流对开裂黏土裂缝的数学模型研究相对较少。

为了准确预测水流作用下的填埋场压实黏土封场系统的物性参数的变化过程，通过COMSOL开展了流体在三条裂缝中流动的仿真研究，建立多孔介质不连续裂缝中水渗流数学模型，模拟研究压实黏土水流作用下的物性参数变化对填埋场压实黏土封场系统开裂，为预测水流作用下压实黏土封场系统物性参数的变化过程提供了依据。

2开裂黏土水渗流数学模型

2.1　流体流速方程

达西定律的应用条件为流体在多孔介质中流动的驱动力为水力势能梯度，通过考虑压力和位置势能的不同，而从流线起点到终点将水力势能场形象化。根据达西定律，通过单位孔隙表面的净通量[11]为：

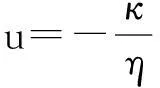
(1)

式中：u为达西流速(m/s)；κ为多孔介质的渗透系数(m2)；η为流体的动力黏度(Pa·s)；p为流体的压力(Pa)；ρf为体密度(kg/m3)；g为重力加速度(m/s2)；▽D为g方向上的单位矢量。其中渗透系数κ表示单位水力梯度下的单位流量，通常表征流体通过孔隙骨架的难易程度。

方程中的水力势能，来自压力p和重度ρfgD。定义g=9.82 m/s2，D=0。D的选择对模拟的结果和其中包括的物理参数有重要影响。例如，如果D是垂直z轴的方向，同时流体流向是完全与xy平面平行的，随着D梯度的变化，流体的驱动力就只有单独的压力梯度。

将达西定律代入连续性方程后得到以下广义控制方程：

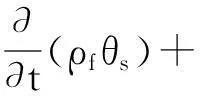
(2)

式中：θs为流体的体积部分；Qs为流体的流量。

对不可压缩流体来说，ρf可以从等式两端约去，因此控制式2可化为：

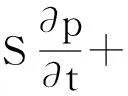
(3)

其中S为相关系数，可用来表示包括在模型中设定固体变形方程或是从其他对温度和浓度的分析结果。COMSOL在其表达式区域内将S定义为利用流体或固体压缩系数求得的指定的系数。应用型达西定律模型采用了式(3)，并同时要求流体是不可压缩的(即流体密度ρf是一个定值)。

2.2　土体基质中水渗流方程

以时间为变量的土体基质中的水流流动方程可以通过达西定律求得：

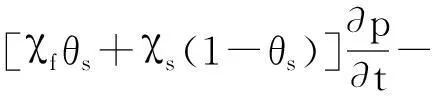
(4)

式中：p为流体压强(Pa)；θs为孔隙率；χf、χs分别为流体和固体的压缩系数(m·s2/kg)；κm为土体渗透系数(m2)；η为黏滞系数(kg/m·s)。

基质模型中已经设定好的流速变量为uesdl(m/s)，给出了达西流速表达式：

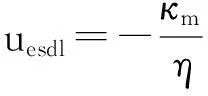
(5)

基质块的所有面上的流量平衡方程为：

n·uesdl=0.

(6)

式中：n为垂直边界向外的单位方向向量。

2.3　基质裂缝中水流流动方程

模型中的裂缝是一系列的内部边界。传统的边界模型定义流体的流动是垂直于边界的而不是沿着边界的。而在这个模型中，可通过从COMSOL软件中特定的切向选项来定义流体是可以沿着内部边界和裂缝中流动的。

因此，为了使定义的这种模型可以有效地实行，必须建立裂缝边界方程来求解和土体基质方程所求得的相同的变量p(压力)。在此模型中，裂缝中流体流速方程是基质流动流速方程(即达西定律)的变形。可以通过改变方程中的相关系数来改变流体在裂缝中流动的阻力系数以此适应达西渗流方程。下式给出了裂缝和土体基质之间的连续性方程：

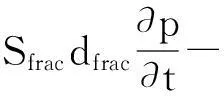
(7)

式中：Sf为裂缝存储系数(m·s2/kg)；κf为裂缝的渗透系数(m2)；dfrac为裂缝的厚度(m)；

由于流动方程中出现了裂缝的厚度，故单位长度上的流量为：

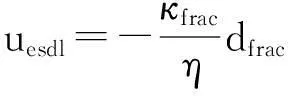
(8)

式中：▽T为裂缝切平面上的梯度算子；裂缝中的线流速为ulin=uesdl/dfrac(m/s)

裂缝的边界条件及假设：(1)出口和入口的压力是已知的；(2)入口的压力是不变的常数；(3)出口的压力是随着时间而线性变化的；(4)其他边界没有流体流入或流出。方程表达式如下：

p=p0.

(9)

p=p0-t·10Pa/s.

(10)

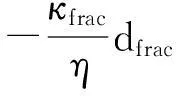
(11)

2.4　平均流速方程

由于流体一般只占多孔介质总体积的10%到50%，因此流体在孔隙通道内的流速会超过达西流速u(大约等于它的2—10倍)，为了明白起见，设定流体在给定的孔隙空间内的流速为平均线流速uα(也叫渗流流速)为：

uα=u/θs.

(12)

式中：θs为流体的体积部分，对于饱和介质而言，θs=0；

2.5　相似系数

应用型达西渗流模型有可供选择的相似系数用来进一步简化分析和减少迭代次数或是进行参数化的运算。这种相似系数的分析模式能够采用双子域计算系统，对包括流体在裂缝中的相对快速流动，多相问题和单独密度等进行耦合计算。由于相似系数的加入，控制方程可采用以下形式：

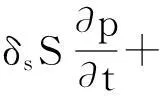
(13)

式中：δs为S的相似系数；δK为渗透系数κ的相似系数；δQ为流量Q的相似系数；

由式1—式5构成水流作用下的多孔介质不连续裂缝中水流流动数学模型。计算参数[12-13]见表1。该模型可开展水流作用下压实黏土封场系统物性参数的变化过程预测与评价研究，对垃圾填埋场封场系统开裂失效的研究具有一定的理论意义。

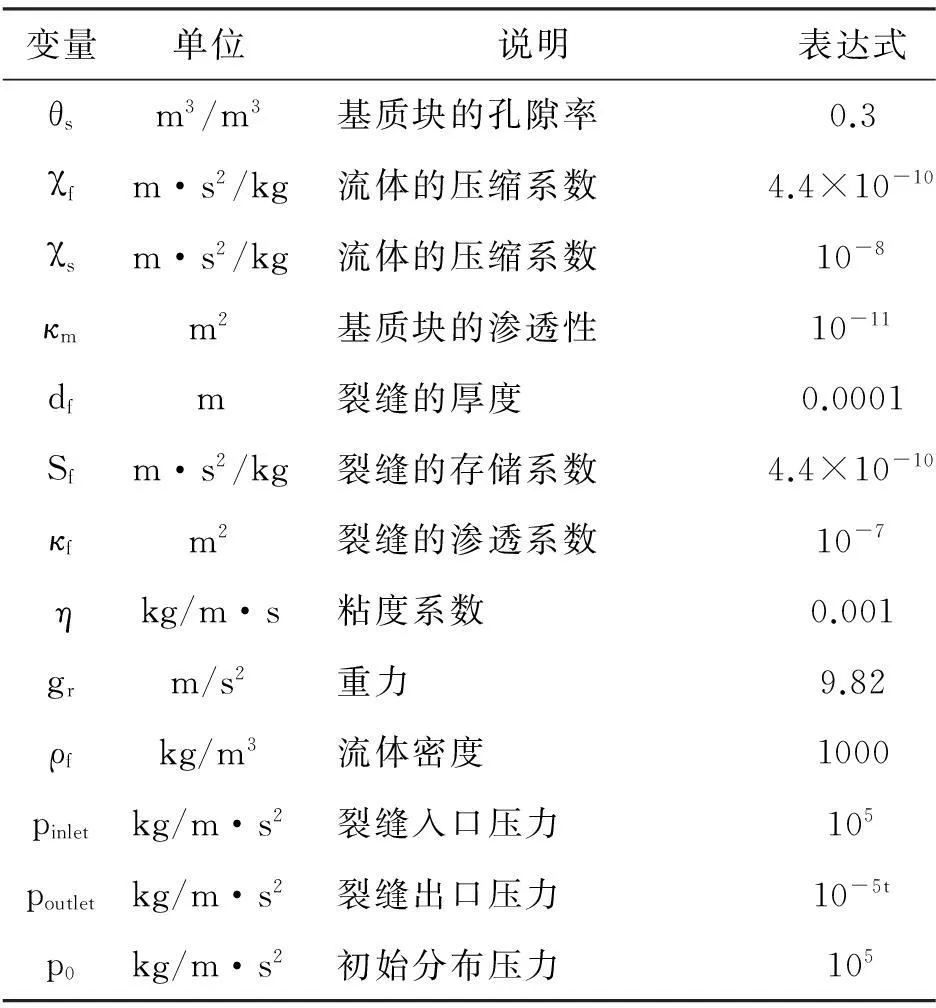
表1　计算参数

3水渗流仿真模型的建立

此模型采用了一种精确高效的方法来模拟开裂基质环境中的裂缝和孔隙中的流动。如图1所示，通过在相邻基质块边界处构造裂缝来建立模型。当设定流体在边界上狭窄的裂缝中流动时，由达西定律来控制基质块中的流速把裂缝作为基质块内部的边界这种模型是非常有效的，这样减少了创建一个几何形状长而窄即具有较高的长宽比的裂缝的必要。否则，需要建立一个由大量微小单元构成的高密度的几何模型。

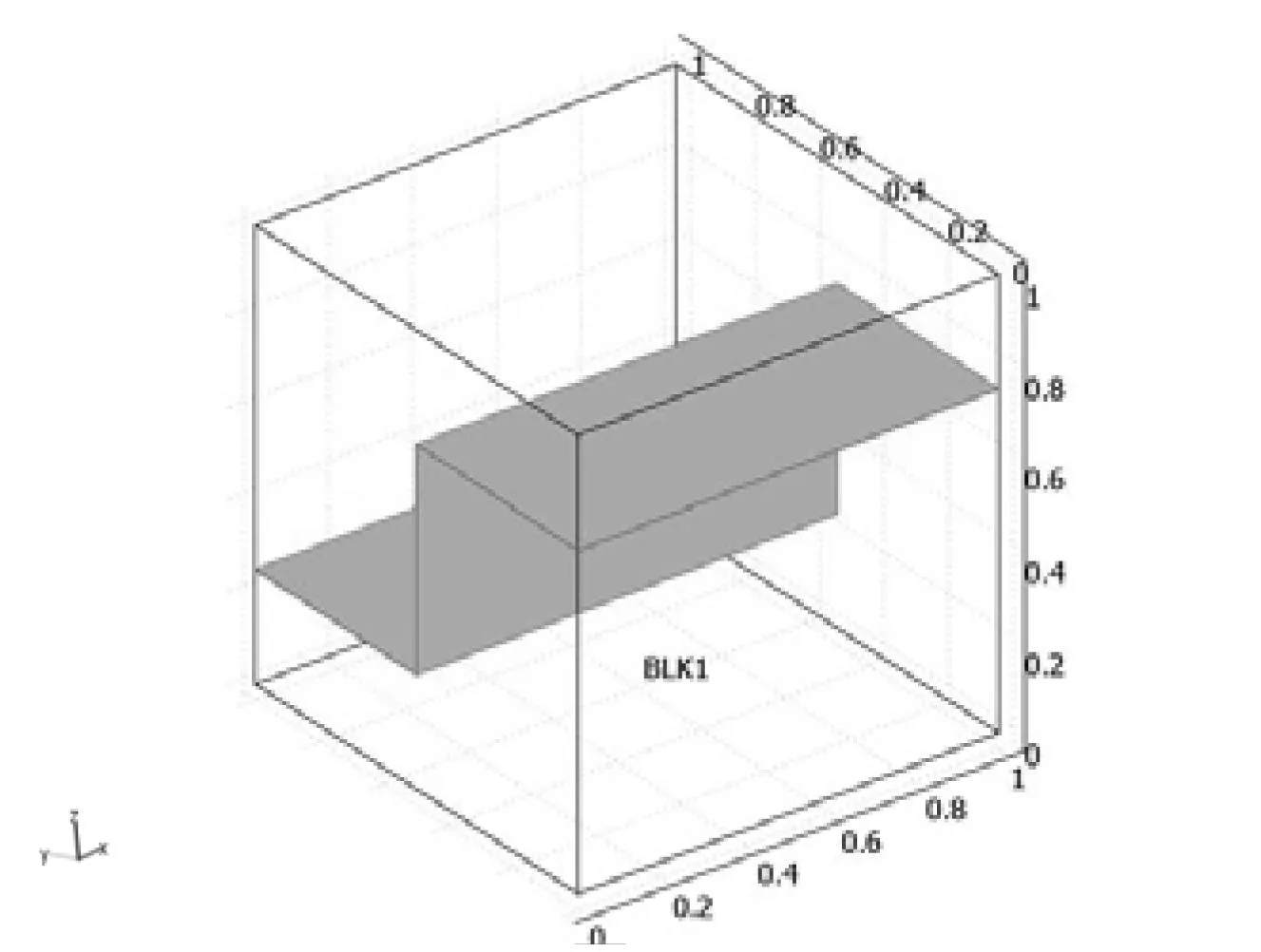
图1　一条裂缝的几何模型

图1所示为一个长宽高各为1 m的开裂的多孔介质基质块。裂缝厚度为0.000 1 m，远小于基质块的厚度。水流在裂缝中的渗透性能远大于基质中渗透性能。除了裂缝的出入口所在的面上以外，基质块其他的平面都是不可渗透的。模型中的流体从基质块的裂缝右上方边缘流向左下方的边缘。在数值计算过程中，最初状态的流体在基质中是不能流动的，仅当裂缝的入口那一侧出现压力梯度时，流体才会在其作用下流动，出口处的压力随时间逐渐减小，入口处的压力仍保持恒定。计算过程约1 000 s。

为了模拟较复杂工况下的压实黏土裂缝中水流流动模型，人工添加了三条裂缝，对其中水流流动进行数值分析及模拟如图2所示。

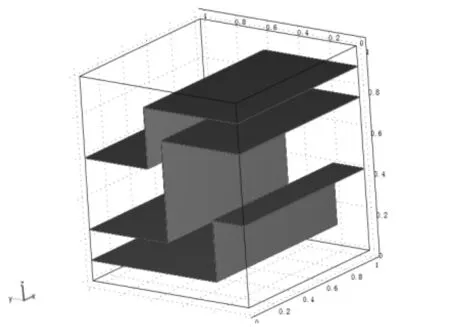
图2　三条裂缝的几何模型

4计算结果与分析

水流在压实黏土裂缝和孔隙中流动过程中所引起黏土物性参数的变化对黏土的抗压，抗剪强度等工程特性造成一定的影响。此处借助多孔介质不连续裂缝水流流动模型对水流在裂缝中流动时的压强和流速变化进行数值计算。

图3表示了在最终输出时间1 000 s时的流体压力等值面图。可以看出，流体的压力在裂缝和基质之间是连续的，等压面成弯曲状表示流体在裂缝中的流动状态与其在土体基质中的流动不同。这是由于裂缝和基质(土颗粒)具有不同的渗透系数所造成的。根据达西渗流定律可知，当水力梯度相同时，流体在介质中的渗流流速与介质的渗透系数成正比[14]。同时，在此过程中流体的压强所出现的最大值和最小值分别出现在入口和出口的边缘处，大小分别为99 kPa和91.5 kPa。

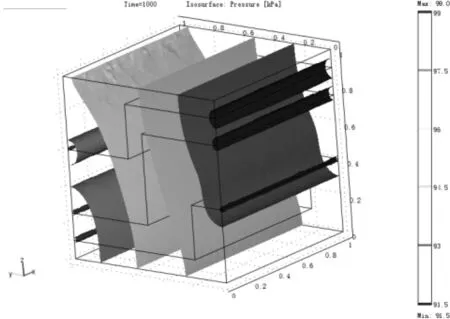
图3　裂缝中水流流动等压面图

由图4可以看出，流体在裂缝中流速较大的区域主要分布在水流的入口和出口处的边缘，这是因为流体在裂缝中流动过程中受到流体与基质边界的摩擦力作用，同时裂缝的宽度对流体流动起到一定的约束作用，进而影响流体在裂缝中的流速场分布。

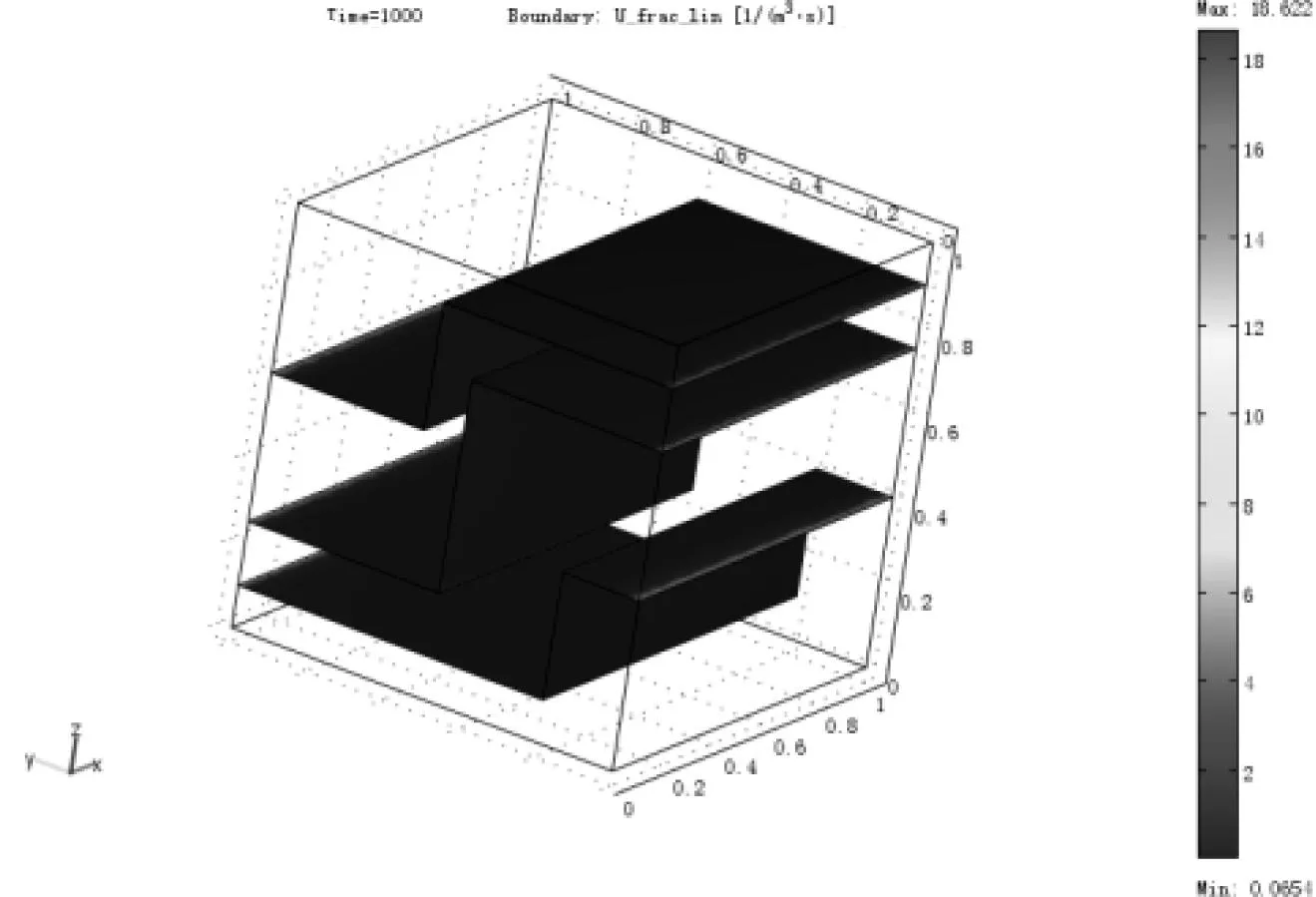
图4　裂缝中水流流动的流速场的分布

由图5分析可得，流体在基质中和裂缝中的流速之比的分布规律在裂缝宽度方向上表现为各向同性。同时，由右侧的数据可以看出，流体在基质中和裂缝中的流速之比最大为0.010 1，并且都出现在流体的出入口两侧，表明水流在这两处的流速与裂缝中的流速相比都比较大。这是由于流体流动方向的两侧都存在压力梯度所导致的。根据达西渗流定律，同种介质中，渗透流速与水力梯度成正比，故在两侧的都存在的水力梯度下，使得出口和入口处的渗透流速远大于裂缝中的渗透流速。同时，由于渗透系数的不同，导致沿着水流方向上的基质渗透流速的变化量远大于裂缝中中流体的流速。所以在上图中会出现基质块的内部区域内，两者流速之比会出现最小值。

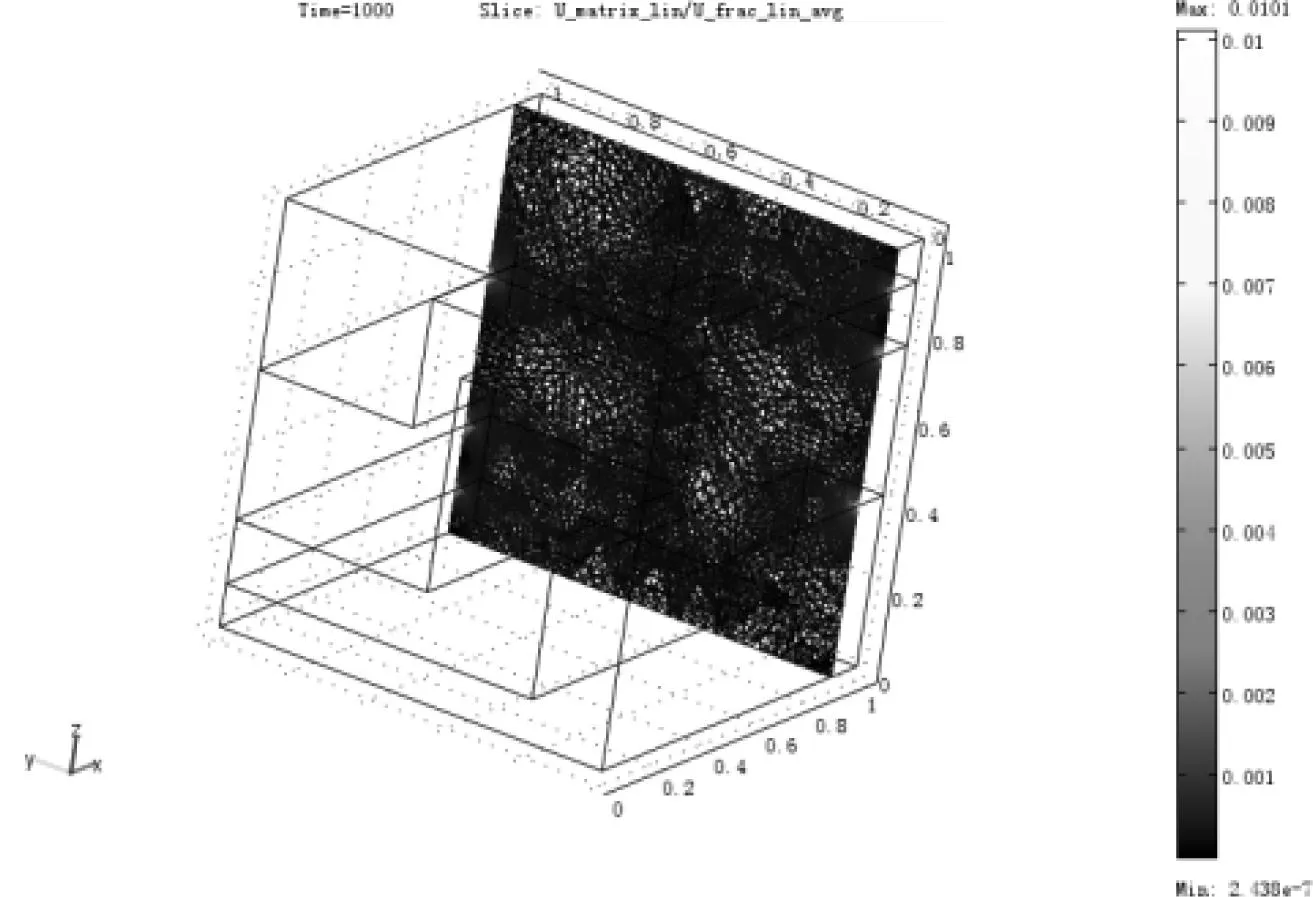
图5　流体在基质中和裂缝中的流速之比(平均线流速)

图6所表现的是以上所有物理量在1 000 s后的运算结果。图中的箭头表示的是流体在基质和裂缝中的流动方向。形象清晰地表达了最终时间状态下的各物理量在空间上的分布情况。由于在建立多孔介质流动模型的时候，假设了流体在其出入口两侧的其他基质块表面没有流入或流出。图6中所出现的箭头表示流体只是从入口流向出口的方向。

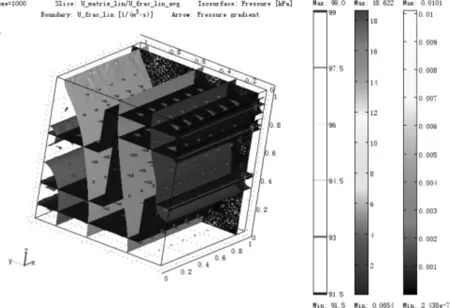
图6　终态流速-压强分布图

为了准确地动态分析水流在裂缝中流动状态，采用时间长度为1 000 s的数值计算过程，其计算结果如图7所示：

通过图7可以看出，通过COMSOL形象的利用多孔介质不连续裂缝水流流动模型模拟压实黏土裂缝中水流流动条件下的流速压强分布。在不同的阶段，基质中的流体流速和等压面的压强随着时间的变化呈现出各自不同的规律。流体的平均线流速场与裂缝中水流流速场在开始很短一段时间内就已经达到稳定状态，其变化规律和之前分析的1 000 s时的规律一样。等压面压强随着时间的推移，由入口向出口依次递减。且等压面的曲率由基质块轴线向裂缝两端递增。表明越靠近裂缝的两端，裂缝中的流体的运动状态与基质中的流动状态差异性越大。水流的流动状态的变化主要体现在裂缝形状的变化上。

图7　不同时间时流速-压强分布图

5结论

通过建立多孔介质不连续裂缝水流流动模型和设定其边界条件来对压实黏土裂缝中水流流动进行数值分析，以评价水渗流条件下对压实黏土开裂的影响，对垃圾填埋场封场系统的安全运行提供理论依据，由仿真计算得出以下结论。

(1)过程中流体的压强所出现的最大值和最小值分别出现在入口和出口的边缘处，大小分别为99 kPa和91.5 kPa；

(2)流体在裂缝中流速较大的区域主要分布在水流的入口和出口处的边缘；由于流体与基质边界的摩擦力作用，以及受到裂缝宽度的影响，对流体流动起到一定的约束作用，进而影响流体在裂缝中的流速场分布.

(3)流体在基质中和裂缝中的流速之比的分布规律在裂缝宽度方向上表现为各向同性，流体在基质中和裂缝中的流速的比值最大为0.010 1，由于渗透系数的不同，导致沿着水流方向上的基质渗透流速的变化量远大于裂缝中中流体的流速。

(4)等压面压强随着时间的推移，由入口向出口依次递减，且等压面的曲率由基质块轴线向裂缝两端递增，表明越靠近裂缝的两端，裂缝中的流体的运动状态与基质中的流动状态差异性越大。

参考文献：

[1]浦辛刚,陈新民.填埋场衬垫系统的评价[J]. 南京工业大学学报,2004,26 (2):33-38.

[2]Baer J U, Kent T F, Anderson S H. Image analysis and fractal geometry to characterize soil desiccation cracks[J].Geoderma,2009.

[3]Tang C, Shi B, Liu C,et al. Influencing factors of geometrical structure of surface shrinkage cracks in clayey soils[J]. Engineering Geology, 2008, 101: 204-217.

[4]袁俊平.非饱和膨胀土的裂隙概化模型与边坡稳定研究[D].南京：河海大学,2003.

[5]刘建国,聂永丰.填埋场黏土衬里破坏机理研究[J].城市环境与城市生态, 2000, 13(6): 51-53.

[6]钱学德,郭志平.填埋场黏土衬垫的设计与施工[J]. 水利水电科技发展, 1997, 17(4): 55-59.

[7]Mathias S A, Todman L C,Step-Drawdown Tests and the forchheimer Equation[J]. Water Resources Resrarch,2010,46(7):1-9.

[8]唐朝生，施斌.干湿循环过程中膨胀土的胀缩变形特征[J].岩土工程学报，2011,33(9):1376-1384.

[9]Pzbek A.Investigation of the effects of wetting-drying and freezing-thawing cycles on some physical and mechanical properties of selected ignimbrites[J].Bulletin of Engineering Geology and the Environment,2014,73(2):595-609.

[10]Peron H, Delenne J Y, Laloui L,et al. Discrete element modelling of drying shrinkage and cracking of soils[J].Computers and Geotechnics,2009, 36:61-69.

[11]王刚,安林. COMSOL Multiphysics 工程实践与理论仿真[M].北京:电子工业出版社, 2012.

[12]徐国建,沈扬,刘汉龙. 孔隙率、级配参数对粉土双轴压缩性状影响的颗粒流分析[J]. 岩土力学, 2013, 34(11):3321-3328.

[13]赵强, 李皋, 肖贵林,等. 单裂隙渗流有限元数值仿真研究[J]. 水资源与水工程学报, 2014, 25(2):195-199.

[14]翟云芳. 渗流力学[M], 北京:石油工业出版社, 2011.

Mathematical simulation of cracking clay in landfill liner under water seepage

DONGYi-qie1,LUHai-jun1，DAIRui1,HELi2

(1.Institute of Poromechanics, Wuhan Polytechnic University, Wuhan 430023，China;2.Department of

Mechatronic Engineering College,College of Arts and Science of Jianghan University,Wuhan 430056,China)

Abstract：Aiming at the problem that the landfill compacted clay cover system is vulnerable to appear desiccation cracking in drought or semi-arid area, based on the Hydrodynamic flow equation, simulate to analyze the mathematical model of water flow in discontinuous cracks in the porous medium, simulate the water seepage rule in crack clay by COMSOL. Based on the results of mathematical simulation, the maximum and minimum values of fluid pressure appear in the inlet and outlet edges, the large area of flow velocity in fluid appear in the inlet and outlet edge in the flow, and closer to the end of cracks, greater the difference in state of motion in fracture fluid and current state of the matrix.

Key words：mathematical simulation; compacted clay; drying and cracking

中图分类号：TP 391.9；TV139.14

文献标识码：A