舰船保障物资优化分配方法研究*
朱 昱 张 健 杜 波 王 磊 张 诗
(1.解放军后勤学院 北京 100858)(2.海军装备部飞机办公室 北京 100071)(3.海军装备部综合计划部 北京 100841)(4.海军航空工程学院 烟台 264001)
舰船保障物资优化分配方法研究*
朱 昱1张 健2杜 波3王 磊4张 诗4
(1.解放军后勤学院 北京 100858)(2.海军装备部飞机办公室 北京 100071)(3.海军装备部综合计划部 北京 100841)(4.海军航空工程学院 烟台 264001)
论文针对实际应用中舰船保障物资分配的需求,提出了动态态势物资分配优化方法,建立了动态态势物资分配优化数学模型,即混合0-1整数规划模型并提供了求解策略。同时利用项目管理方法,提出了保障物资分配项目实施方案的优化流程。
舰船保障物资; 优化分配; 方法研究
Class Number TP393
1 引言
舰船保障物资优化分配方法通常采用固定态势物资分配优化方法。事实上,在舰船保障物资优化分配中,经常出现保障物资供应点位置固定,但作战单位位置不确定的情况。本文针对这一类动态态势物资优化分配问题,建立相应的优化模型并进行求解,得到其最优解或准最优解,达到优化舰船物资分配的目的。
2 固定态势物资分配优化方法
舰船保障物资优化分配需要综合考虑作战单位需求程度的优先级、作战单位的可到达性等多方面问题。固定态势物资分配优化方法(即单供应点多作战单位物资分配优化方法和多供应点多作战单位物资分配优化方法)作为一种物资分配形式在和平时期使用得较为广泛。
2.1 单供应点多作战单位分配策略
单供应点多作战单位是常见的一种物资分配形式(其结构图如图1所示)[1~2]。适用于和平时期舰船保障物资的分配,其分配原则一方面主要是按照作战单位的需求迫切程度由急到缓进行分配(如图2所示)[3~4]。另一方面对于同一作战单位,需比较该单位物资需求量和供应点剩余的物资量:如果前者小于后者,表示剩余物资量充足,作战单位的需求将全部得到满足;如果前者大于后者,表示剩余物资量不足,此时应使用基于最小方差原则的资源公平分配模型,使得单位资源满足需求的偏差最小化。
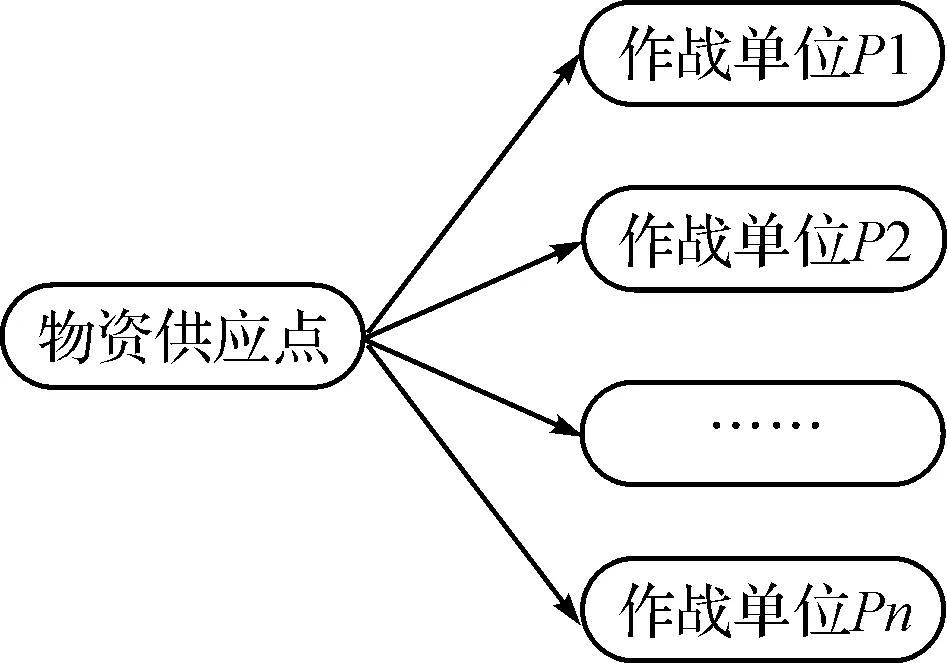
图1 单供应点多作战单位分配结构图
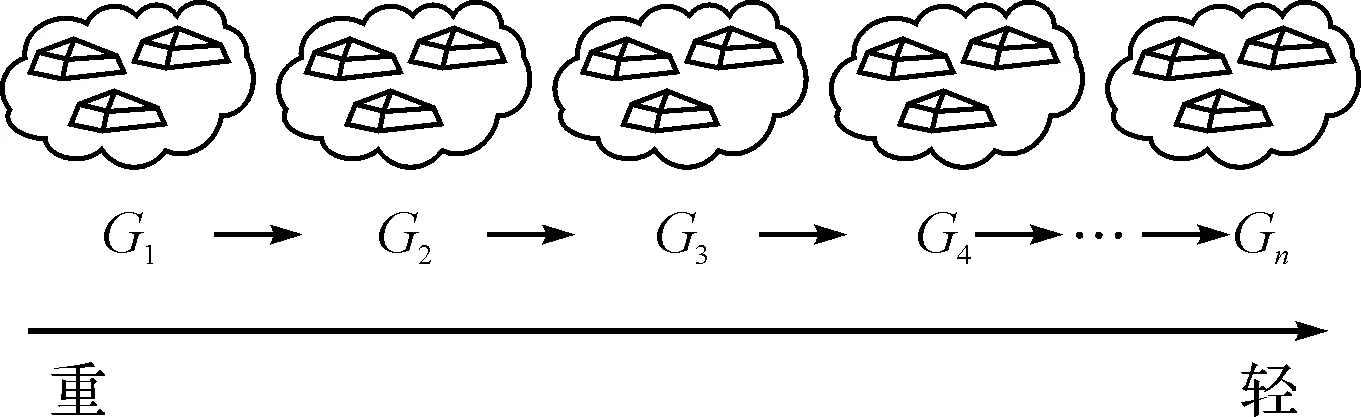
图2 基于需求迫切程度优先的分配示意图
2.2 多供应点多作战单位分配策略
多供应点多作战单位的分配方式可在较短的时间内完成物资的分配,具有较高的分配效率,特别是在舰船保障物资优化的分配过程中,保障基地有多个供应点,且前方有多个作战单位,任一供应点到任一作战单位的距离是已知的,要求尽量缩短各供应点到各作战单位配送的时间,使得各个作战单位得到物资的总体满意度最大[5~6]。其结构示意图和分配示意图分别如图3、图4所示[7~8]。
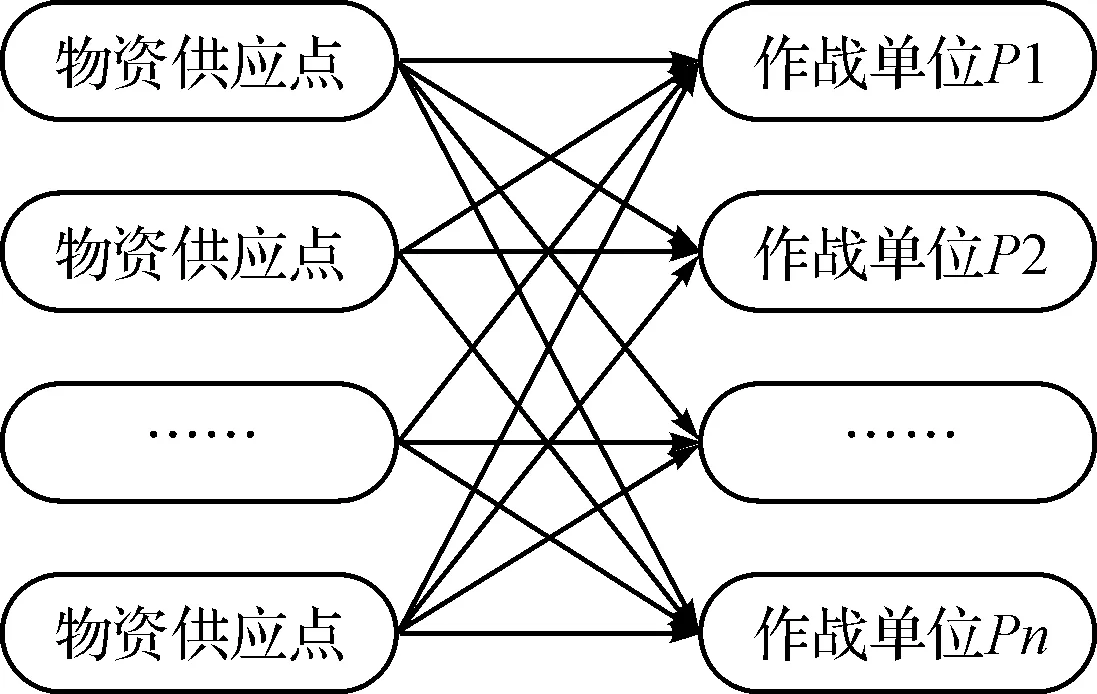
图3 多供应点多作战单位分配结构图
图4 多供应点多作战单位分配示意图
在和平时期,固定态势物资分配优化方法是一种较为常用的分配方法。但在实际使用上,经常出现保障物资供应点位置固定,但作战单位位置不确定的情况。特别是战时,如几艘不同的舰船分别在不同海域执行任务,由于任务要求,需要靠码头进行物资补给,由于返航时间不尽相同,舰船选择停靠的码头也不一定相同,这对物资分配优化提出了新的需求。
3 动态态势物资分配优化方法
3.1 动态态势物资分配优化模型
3.1.1 物资分配路径模型建立
针对具体问题,首先建立供应点和保障点路径模型。

图5 供应点和保障点路径模型
1) 供应点与供应点之间车辆运输时间
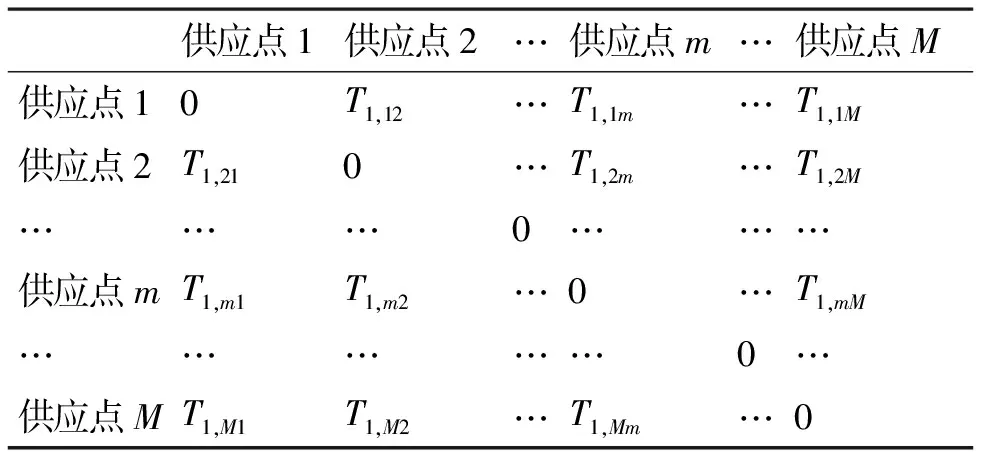
表1 供应点与供应点之间车辆运输时间
2) 供应点与补给点之间的车辆运输时间
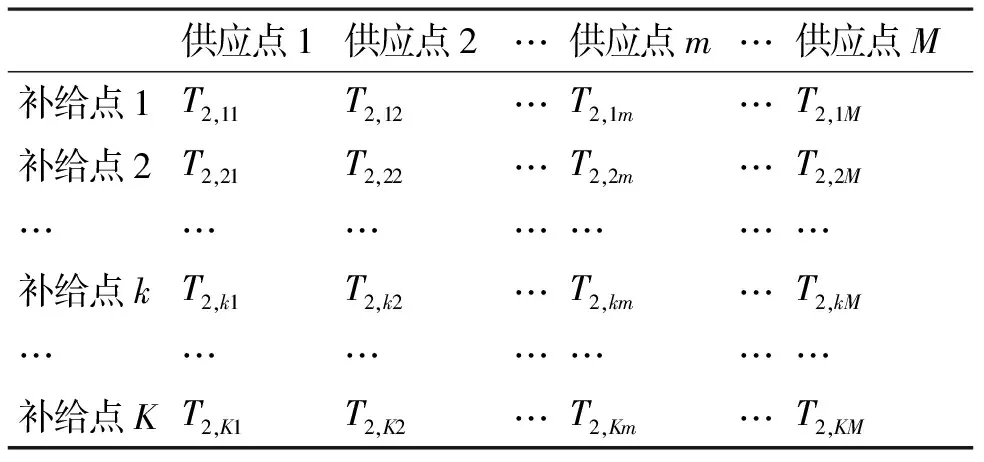
表2 供应点与补给点之间的车辆运输时间
3) 补给点与补给点之间的航行时间

表3 补给点与补给点之间的航行时间
4) 舰船与补给点1之间最短航行时间
舰船与补给点1之间的最短航行时间为:T4,11,T4,12,…,T4,1n,…,T4,1N。
以上航行时间和车辆行驶时间均视为已知量。
3.1.2 库存模型及需求模型建立
1) 库存模型
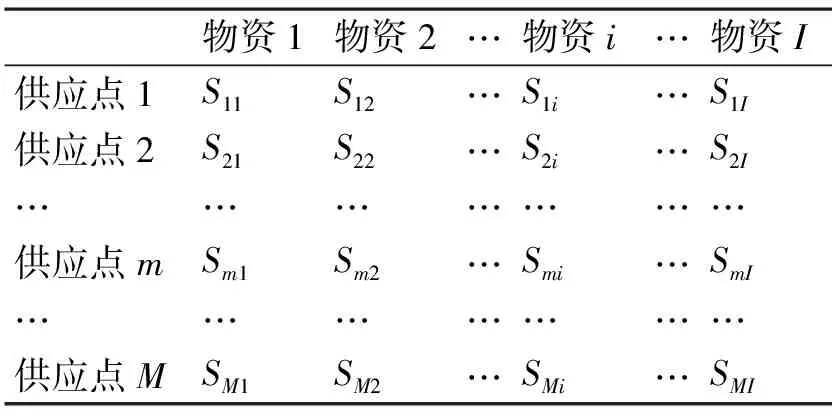
表4 供应点库存模型
2) 需求模型
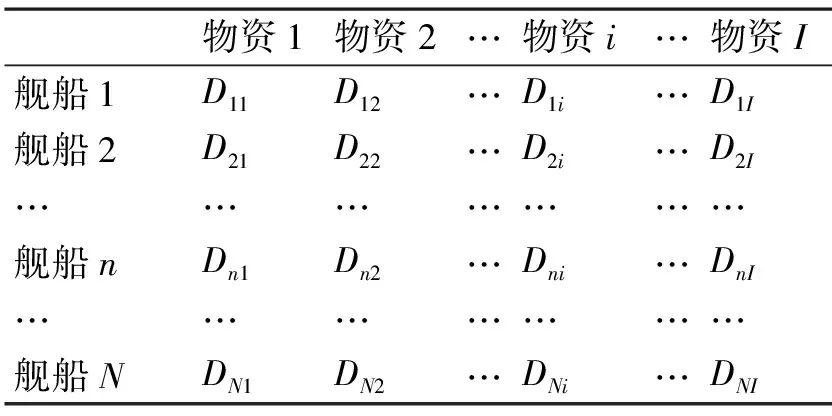
表5 各舰船需求模型
3) 供应点与补给点之间对应关系模型
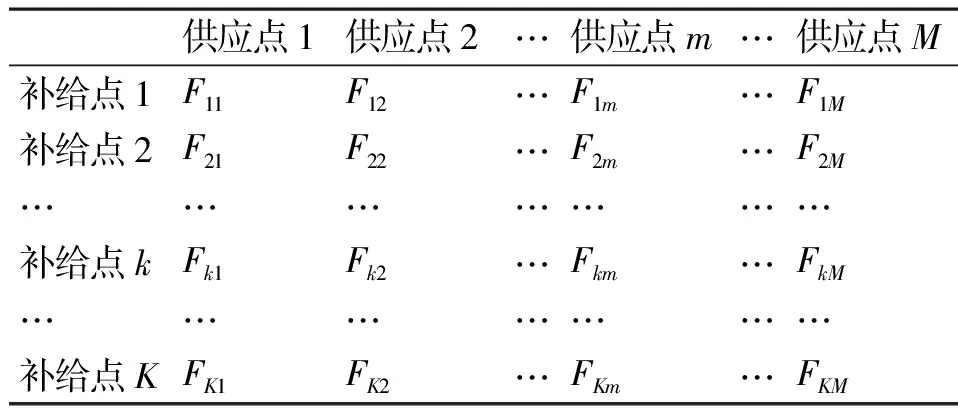
表6 供应点与补给点之间对应关系模型
各供应点物资库存和各舰船需求均视为已知量。Fkm=1表示第k个补给点的物资由第m个供给点供给;Fkm=0表示第k个补给点的物资不由第m个供给点供给。
3.1.3 定义优化变量
在动态态势物资分配优化分配问题中,优化的目标是获得最优的舰船选择补给点(码头)方案和各供应点之间的物资调配方案,因此定义如下的优化变量:
1) 舰船选择补给点(码头)方案优化变量
对于舰船n,定义向量
(1)
定义相应约束条件,即xn1,xn2,…,xnk,…,xnK只能取0或1,且
(2)
其中xnk=1表示舰船n选择第k个补给点进行靠码头补给;反之xnk=0表示舰船n不选择第k个补给点进行靠码头补给。
对于N个舰船,可以定义N个类似的向量X1,X2,…,Xn,…,XN及N组约束条件:
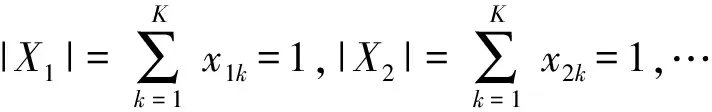
(3)
特别地,当补给点数量只有2个时,上述定义可以简化:舰船n只用一个未知数x即可表示对补给点的选择结果,如x取0表示选择补给点1,取1表示选择补给点2。
2) 各供应点之间物资调配方案优化变量
对于供应点m,定义矩阵
(4)
其中,矩阵元素ym,i,1表示第m个供应点从第1个供应点调配的第i种物资的数量,ym,i,2表示第m个供应点从第2个供应点调配的第i种物资的数量,其余类似。
上述矩阵元素的取值可以认为只取整数(假定物资都以整数为单位),并且不能超过库存,即有如下约束条件:
0≤ym,1,1≤S11,0≤ym,1,2≤S21,…,0≤ym,I,M≤SMI
(5)
相应地,对于M个供应点,可以定义M个矩阵Y1,Y2,…,YM,用于表示各供应点物资调配数量,相应地有M组约束条件:
0≤y1,1,1≤S11,0≤y1,1,2≤S21,…,0≤y1,I,M≤SMI
0≤y2,1,1≤S11,0≤y2,1,2≤S21,…,0≤y2,I,M≤SMI
…
0≤yM,1,1≤S11,0≤yM,1,2≤S21,…,0≤yM,I,M≤SMI
(6)
3.1.4 各补给点物资需求及各供给点需要提供的物资总量计算
根据舰船选择补给点(码头)方案优化变量X1,X2,…,Xn,…XN和表5所示的各舰船需求数据,可以计算得到每个补给点的物资需求。
第k个补给点对第i种物资的总需求为
(7)
从而第k个补给点对各种物资的总需求Rk1,Rk2,…,RkI也可以计算得到。
由于补给点和供给点之间的对应关系已经确定,故与第k个补给点对应的供给点的物资总需求也可以确定。
(8)
故第m个供应点需要提供各种物资的总量RFm1,RFm2,…,RFmI也可以计算得到。
3.1.5 供应点之间物资调配约束条件
当第m个供应点的第i种物资库存满足对应的补给点需求时,不需要从其它供应点进行物资调配,只有第m个供应点的第i种物资库存不满足对应的补给点需求时,才需要从其它供给点进行物资调配,因此有如下约束条件:
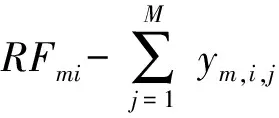
(9)
对于I种物资,有I组约束条件,即
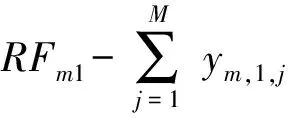
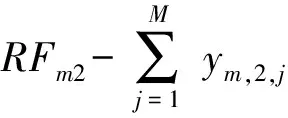
…
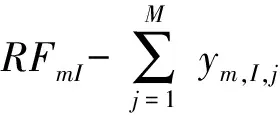
(10)
对于M个供应点,有M×I组约束条件,即
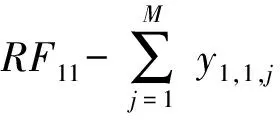
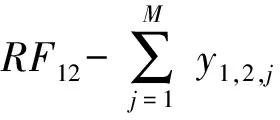
…
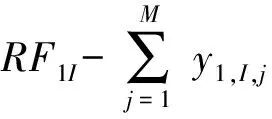
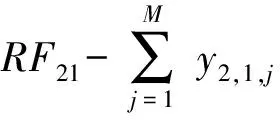
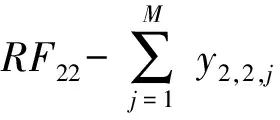
…
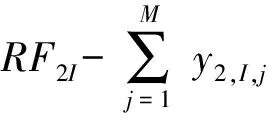
…
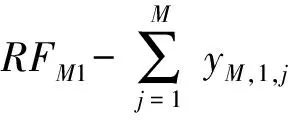
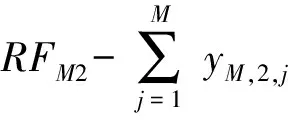
…
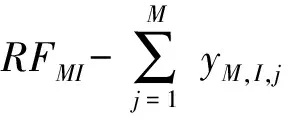
(11)
3.1.6 舰船航行及物资调配总成本计算
定义舰船每小时航行成本系数为c1,车辆每小时运输成本系数为c2,假定每个单位的物资都可以装满1车,根据3.1.1~3.1.5的模型及变量定义,可以计算总成本。
1) 舰船航行成本
(12)
2) 供应点之间物资调配运输成本
(13)
3) 供应点向补给点运输成本
(14)
故总成本为
C=C1+C2+C3
(15)
3.2 混合0-1整数规划模型及求解
综合3.1.1~3.1.6的模型,可以得到式(16)的动态态势物资分配优化数学模型。由于优化变量取值范围均为整数,且部分变量只能取0或1,因此这是混合0-1整数规划。
对于混合0-1整数规划的求解,在优化变量维数不太大的情况下,可以采用隐枚举法结合分枝定界法求解,当优化变量维数很大的情况下,计算量将呈指数增加,耗时较长,这时可以采用遗传算法、粒子群算法等优化算法进行求解[9~10]。对于隐枚举法结合分枝定界法求解,可以通过Matlab编程实现,也可以通过Excel或Lingo等软件实现[11~13]。隐枚举法求解混合0-1整数规划的算法流程如图6所示。
(16)
3.3 基于项目管理方法的实施方案优化
根据3.1的物资分配优化模型及3.2的混合0-1整数规划模型求解后,可以得到最优的舰船选择补给点方案和物资供应点之间的物资调配方案。这样,动态态势物资分配方案最终可以确定。
确定动态态势物资分配方案后,可以根据项目管理的方法对物资分配实施方案进行进一步优化,使实施方案总工时和配送运输资源、各舰船作业时间得到进一步优化。优化流程如图7所示。
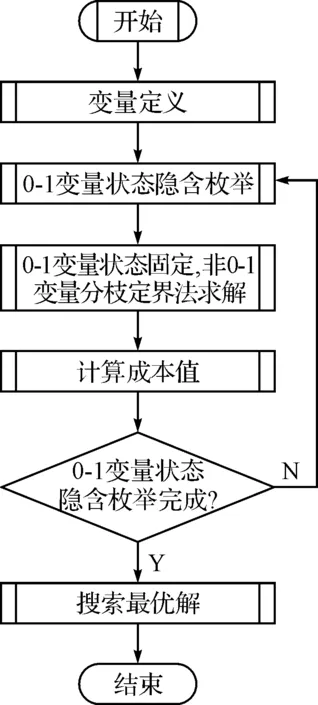
图6 隐枚举法求解混合0-1整数规划的算法流程
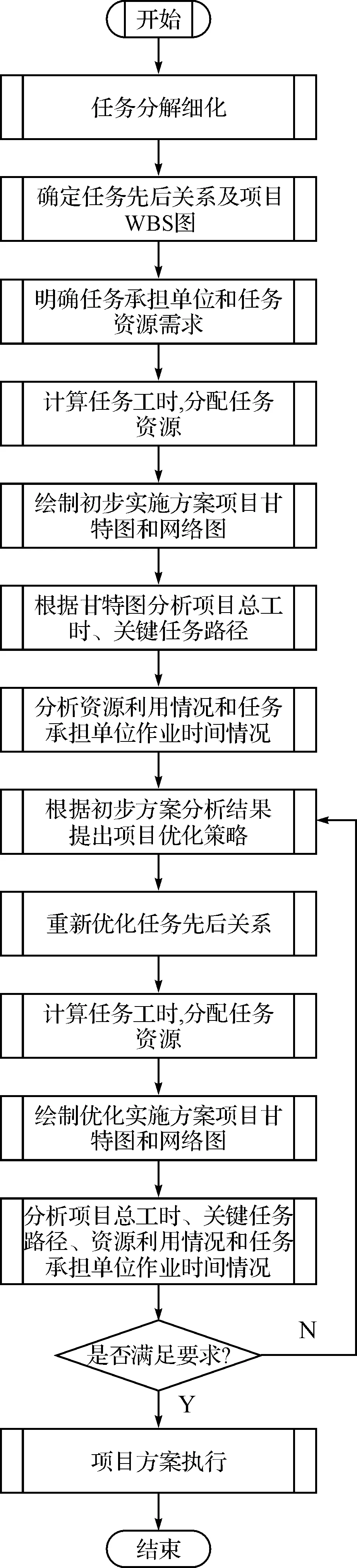
图7 采用项目管理方法的实施方案优化流程图
4 结语
本文通过对一定条件下舰船保障物资优化分配问题进行研究,得出的结论对于制定物资分配方案具有一定的参考价值。需要指出的是舰船保障物资优化分配受到运输规划、仓储管理、货物配装、需求预测等诸多因素的影响。因此,在实际应用时应综合权衡各个因素,一方面要与定性分析密切结合,另一方面要在保障演习实践中不断地修正和完善。
[1] 骆义.物流配送车辆调度优化研究[D].大连:大连海事大学,2013:98-107.
[2] 袁庆达,杜文.带有时间窗的混合车队车辆路径问题的模型与算法研究[J].西南交通大学学报,2011(4):7-12.
[3] 张丽萍,柴跃廷,曹瑞.有时间窗车辆路径问题的改进遗传算法[J].计算机集成制造系统,2012(2):18-22.
[4] 姜大立,杨西龙,杜文,等.车辆路径问题的遗传算法研究[J].系统工程理论与实践,2009(6):13-18.
[5] Xu J, Kelly J. P. A network flow~based tabu search heuristic for the vehicle routing problem[J]. Transportation Science,2010(3):43-52.
[6] Hooker J. N, Natraj N. R. Solving a general routing and scheduling problem by chain declmposition and tabu search[J]. Transportation Science,2009(2):6-12.
[7] Gendreau M, Hertz A. tabu search heuristic for the vehicle routing problem[J]. Managememt Science,2012(4):33-42.
[8] 李军.车辆调度问题的分派启发式算法[J].系统工程理论与实践,2012(1):26-27.
[9] 冷德惠,张金梅,李大卫.遗传算法在有时间窗车辆路径问题上的应用[J].系统工程理论与实践,2010(8):17-19.
[10] 刘民.遗传算法方法及其在生产线调度问题中的应用与研究[D].北京:清华大学,2007.
[11] 李军.非满载车辆调度问题的遗传算法[J].系统工程理论方法应用,2010(3):31-33.
[12] Balakfishnan N. Simple heuristics for the vehicle routing problems with soft time windows[J]. Journal of Operational Research Society,2013(3):11-12.
[13] Desrocher M, Desrosiers J, Solomon M. A new optimization algorithm for the vehicle routing problem with time windows[J]. Operations Research,2012(2):24-25.
Method of Optimized Distribution of Material Support of Ships and Warships
ZHU Yu1ZHANG Jian2DU Bo3WANG Lei4ZHANG Shi4
(1. Logistics Academy of PLA, Beijing 100858)(2. Plane Office of Naval Equipment Department, Beijing 100071)(3. Synthesizing Plans Ministry of Naval Equipment Department, Beijing 100841)(4. Naval Aeronautical and Astronautical University, Yantai 264001)
Based on the demand of material support of ships and warships allotment in practical application, an optimization method of dynamic material allotment is put forward. A mathematical model of optimization of dynamic material allotment is established. A mixed 0-1 integer programming model and solving strategies is provided. Based on the method of project management, an optimized flow of the project for implementation of material support allotment is put forward.
material support of ships and warships, optimized distribution, method study
2014年9月12日,
2014年10月27日
朱昱,女,研究方向:军队卫生勤务。
TP393
10.3969/j.issn1672-9730.2015.03.031

