S型竖向不规则框筒混合结构地震响应分析

佘钊钊，雷庆关,2

(1.安徽建筑大学，安徽 合肥 230601；2.合肥工业大学，安徽 合肥 230009)



S型竖向不规则框筒混合结构地震响应分析

佘钊钊1，雷庆关1,2

(1.安徽建筑大学，安徽 合肥 230601；2.合肥工业大学，安徽 合肥 230009)

摘要：利用SAP2000有限元软件，对建立的竖向不规则框筒混合结构进行了模态分析，得到了结构自身的动力特性。在此基础上，利用反应谱分析和时程分析对结构响应的结果进行数值模拟，得到了结构的抗震性能，为设计工作提供了一定参考。

关键词：竖向不规则；反应谱分析；时程分析；抗震性能

0　引　　言

体系复杂和不规则的结构容易在地震中产生严重的破坏，给人们的生命财产造成严重的损失。为了满足抗震性能及经济合理性，《建筑抗震设计规范》GB50011-2010(以下简称《抗规》)要求我们应尽可能选用规则的形体[1]。但是，随着经济社会的发展，火柴盒式的建筑已经不能满足人们的审美需求。在工程实践中，由于场地限制、底层层高加高、错层、楼板开洞、抽柱等原因，越来越多的竖向不规则建筑出现在人们的视野中。对于此类不规则建筑，我们应研究分析结构的抗震性能，使结构在地震作用下不超过规定的限制，从而保证建筑物的安全性。

本文通过SAP2000建立一栋S型框筒混合结构模型，对其进行模拟分析，了解其动力特性，掌握结构的抗震性能，判断其抗震的合理性，为以后的设计提供一定的理论基础。

1　竖向不规则的内容及分类

竖向不规则分为刚度不规则、强度不规则和质量不规则。由于楼层高度的改变、竖向抗侧力单元的中断、非结构单元设计不合理等原因导致结构竖向刚度不连续称为刚度不规则。竖向刚度不连续楼层称为“软层”，“软层”容易造成层间位移增大，发生应力集中和弹塑性变形集中现象，从而导致软层及以上建筑物的损毁甚至整栋建筑物的倒塌。研究表明[2][3]，结构底层刚度减小20%时，层间位移需求增大要达到100%，当采取结构不同但强度一致的模型时，结构底层刚度减小30%，层间位移可增大20%～40%。强度不规则是由于结构抗侧力单元(柱、剪力墙等)截面尺寸偏小或纵向配筋不够等原因，造成结构位移分布模式发生改变，引起结构的弹塑性行为集中，导致结构局部或整体的不稳定。结构的质量不规则是通过比较楼层之间重力荷载代表值判断的。建筑抗震设计用的重力荷载是结构构件永久荷载的标准值和竖向可变荷载的组合值之和[1]。结构质量分布不规则会影响结构的动力反应，导致结构侧向惯性作用力增大，延性减小。

2　模型的建立及其动力特性的分析

2.1计算模型的建立

本文通过SAP2000建立一栋S型外框内筒混合结构，该结构呈现出竖向抗侧力构件不连续，楼层凸出与收进等竖向不规则特点。建筑共十五层，首层高5m，2-3层高4m，4-15层高3m，总高度49m。房屋长48m，宽40m，柱距为8m，平面为矩形。剪力墙与楼板均采用C35混凝土，其中楼板厚200mm，剪力墙厚250mm。钢材均采用Q345钢，框架柱截面采用400×400×30×50H型钢，主梁截面采用400×400×20×35H型钢，次梁截面采用300×300×15×15H型钢，斜撑采用400×400×15×15H型钢。结构楼面恒载4KN/m2，活荷载2KN/m2，外墙线荷载7KN/m，抗震设防烈度为8度，地面加速度为0.2g，场地类别为二类，设计地震分组为第二组，结构阻尼比为0.05，场地特征周期0.40s，周期折减系数0.85，模型如图1所示。

2.2结构动力特性分析

模态分析又称为振型叠加法动力分析，用于确定结构的振型[4]，是研究结构动力特性的一种方法。通过模态分析，可以求出结构的自振周期和频率等基本参数，帮助设计人员认识结构的自身特性。模态分析还是其他动力分析的基础，包括反应谱分析和时程分析。在模态分析中，要采用适当的方法对耦合线性结构进行解耦，SAP2000中提供了特征向量法以及Ritz向量法，本文选取程序默认的特征向量法进行分析。

对图1所示模型进行模态分析，结构质量源定义为来自荷载，按规范[1]规定，自重、附加恒荷载的系数为1.0，活荷载系数为0.5。考虑到结构振型参与质量不应小于总质量的90%，本文振型数量选为15个，不考虑频率偏心。结构质量参与系数分析结果见表1。

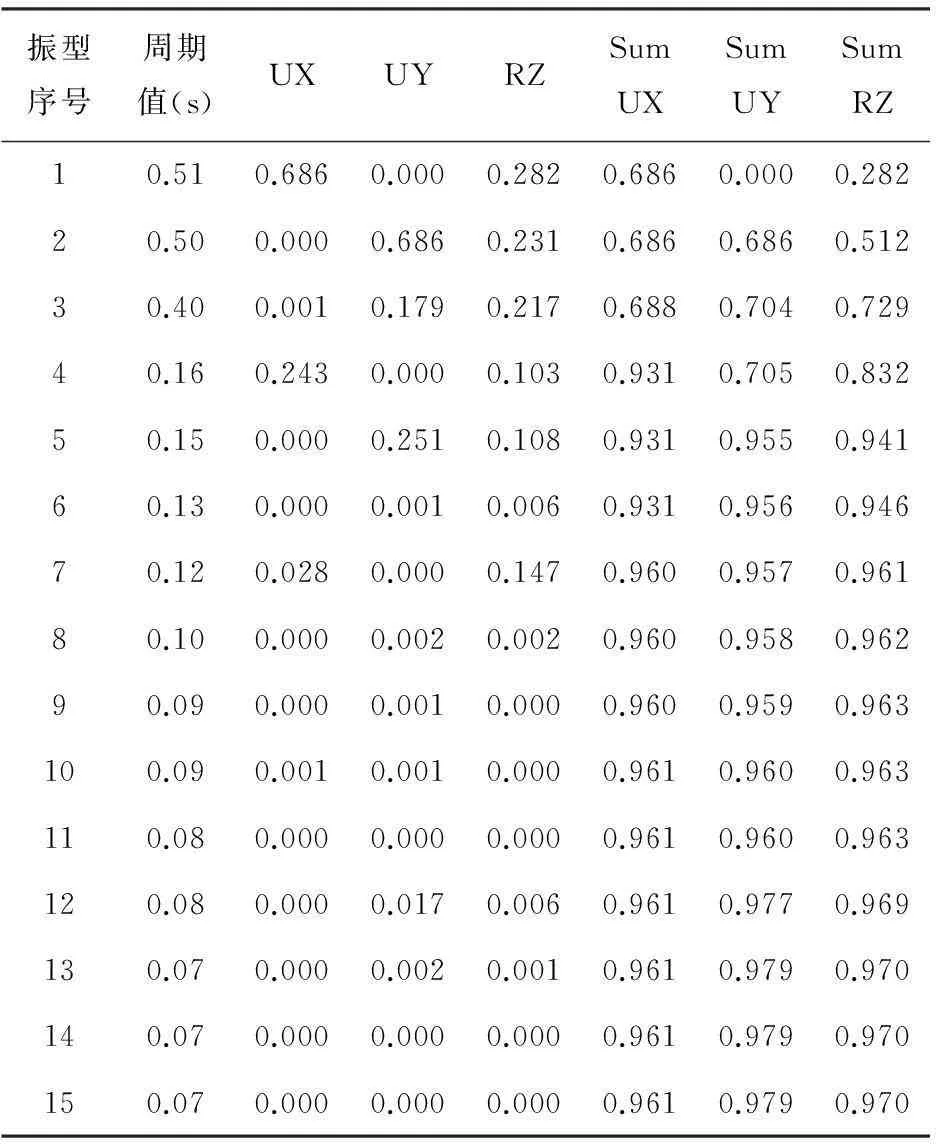
表1　模型质量参与系数输出信息

通过分析模型的自振特性，可以得出以下结论：第一振型周期为0.51s，质量参与系数UX为0.686，远远大于UY的0.000，且两者之和大于RZ的0.282，所以第一振型以沿X方向为主；第二振型周期为0.50s，UX为0.000，UY为0.686，两者之和大于RZ，而且UY远大于UX，故第二振型以Y方向平动为主；第三周期为0.40s，UX与UY之和为0.180，小于RZ的0.217，所以第三振型是以扭转为主的振型。由于结构不对称，质量和刚心不重合，所以结构在高阶振型中出现了扭转效应，而且悬挑部分还带有竖向震动。

《抗规》中要求，当对结构应用反应谱法进行抗震分析时，振型质量参与系数不小于0.9[1]，本文前15阶振型质量参与系数SumUX为0.961、SumUY为0.979，均满足规范要求。

《高层建筑混凝土结构规程》JGJ 3—2010(以下简称《高规》)中要求，混合结构高层建筑及复杂高层建筑以扭转为主的第一周期Tt与平动为主的第一周期T1之比不应大于0.85[5]，本文两者周期之比为0.784，满足规范要求。

3　结构抗震理论及计算结果分析

3.1振型分解反应谱法及计算结果分析

竖向不规则结构，由于相邻楼层的凹进凸出，使的结构刚心和质心不重合，则势必会出现扭转效应。所以在求解结构地震作用时，应考虑结构的平扭藕联效应，采用CQC法，直接按照双向地震来计算扭转影响，其值可采用下列公式的较大值：

(1)

(2)

式中 0.85—地震作用下考虑x,y方向不会同时达到最大值采用的折减系数；

Sx,Sy—分别为仅考虑x,y单方向水平地震作用下按式(3)、(4)计算的扭转效应；

(3)

(4)

式中SEK—扭转的单向水平地震作用效应标准值；

ρjk—j振型和k振型的藕联系数；

Sj,Sk—为j振型和k振型地震作用效应标准值；

ζj,ζk—j振型和k振型的阻尼比；

λT—j振型和k振型的自振周期比。

本文按XY双向地震作用对结构进行反应谱分析，双向地震的组合为SX+0.85SY，通过SAP2000进行反应谱分析，得出结构的楼层位移与层间位移角见表2：

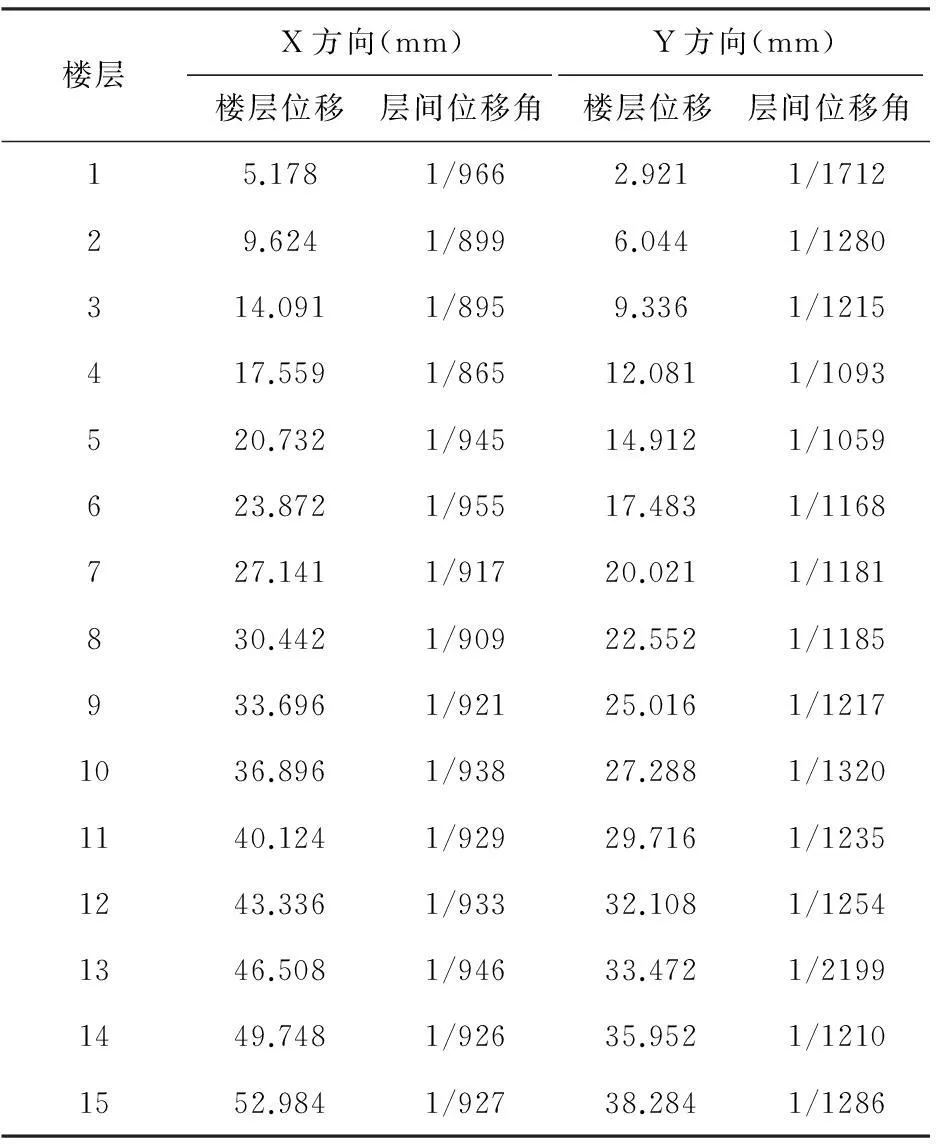
表2　反应谱分析下结构的楼层位移和层间位移角

结构在地震作用下反应谱分析的楼层位移包络图以及层间位移角包络图如图2、图3所示：

结构在地震作用下反应谱分析计算结构见表3：

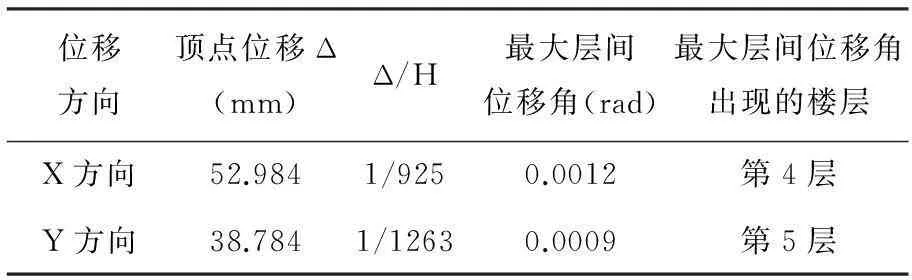
表3　反应谱计算结果

从以上图表中可以看出：结构X方向的位移普遍高于Y方向，说明X方向的抗侧移能力弱于Y方向，这主要与结构形状和楼层的凸出凹进有关。在地震力作用下，结构两个方向上的顶点位移都比较大，分别达到了52.984mm和38.784mm，Δ/H虽然满足了规范的要求，但仍给居民一种不安全感。

结构的层间位移角能反映出楼层的薄弱情况，从表中可知，两个方向的最大层间位移分别为1/865和1/1059，虽然满足《抗规》要求的框架—核心筒弹性层间位移角小于1/800的限值，但与其值比较接近。结构的最大层间位移分别出现在第4层和第5层，说明结构竖向构件不连续造成了该楼层塑性变形集中。在设计时，应采取增大其竖向构件的截面等措施来满足抗侧力刚度的要求。

3.2结构线性时程分析

时程分析法是一种直接动力分析方法，与反应谱法相比，时程分析方法更为先进，它能反映出各个时刻各质点的位移、速度、加速度及各构件的内力[4]，在设计中，它可以校核结构刚度、承载力等方面的薄弱部位。《抗规》中规定，对不规则建筑，应采用时程分析法对结构进行多遇地震下的补充计算。在模拟分析时，选择不同的地震波对结构的抗震分析至关重要。一般情况下，选择地震波有两种方法[6]：(1)记录的天然地震波；(2)人工模拟地震波。采用时程分析法时，应选用不少于两组的天然地震波和一组人工模拟的地震波。本文选用了EL-Centro波、Taft波和一条人工模拟的Lanzhou波进行计算，所得最大层间位移和层间位移角见表4：

时程分析下各楼层最大位移包络图和顶层位移时程曲线包络图见图4、图5：

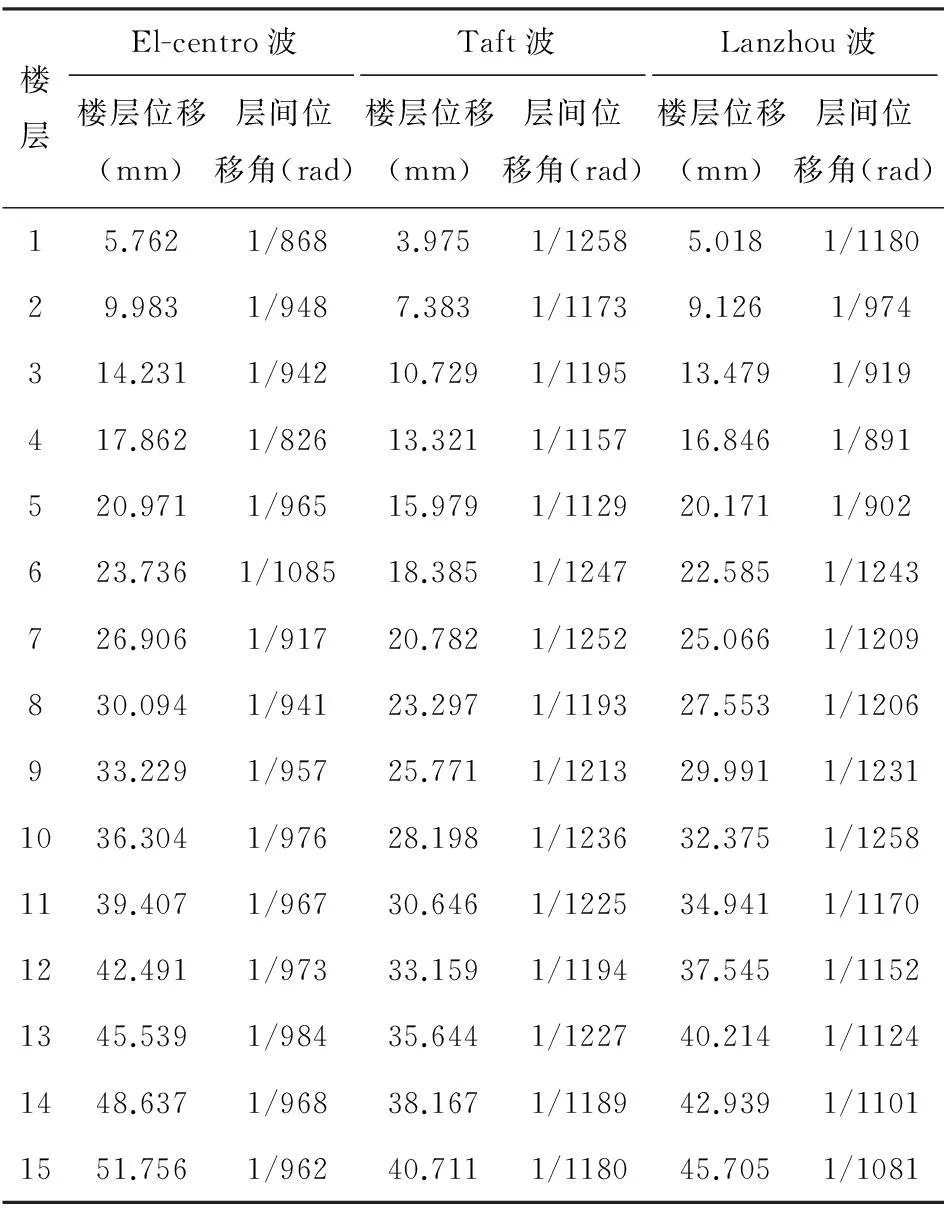
表4　时程分析下楼层的最大位移与层间位移角

从图4中可以看出，在不同的地震波作用下，结构的最大层间位移发生在El-centro波下，结构的最大位移为52.756mm，总位移角Δ/H为1/962，满足《抗规》的要求。图5中反映了结构在不同地震激励下的不同反应，虽然经过换算后输入的地震波峰值相同，但结构的反应还是有显著的差别，这说明了地震波的特性对结构的分析有很大的影响，所以在结构分析前，我们应合理的选择地震波。

4　小结

本文通过SAP2000，对建立的竖向不规则模型进行了动力特性、地震响应分析，可以得出以下结论：

(1)结构的第一振型是沿X方向的平动，在高阶振型中结构出现了一定的扭转，且悬挑部分有竖向震动，说明结构的竖向布置、质量的分布对结构的动力特性有很大的影响。在设计时，工程师应合理的布置结构，尽量使质心与刚心重合，从而避免结构产生过大的扭转致使楼层倒塌。

(2)结构竖向构件不连续的第4层和第5层，对地震作用比较敏感，发生的水平侧移最大，说明了结构薄弱层的抗侧移刚度需求很大。在工程应用中，我们应当提高薄弱层竖向构件剪压比、轴压比及配筋率的抗震等级，增大可能出现塑性变形集中的构件的延性，避免脆性断裂，保证结构始终处于安全限值范围内。

参考文献

1GB 50011—2010 建筑抗震设计规范[S].北京: 中国建筑工业出版社,2010.

2Fernandez J. Earthquake response analysis of buildings considering the effects of structural configuration[C]. Bulletin of the International Institute of Seismology and Earthquake Engineering,Tokyo,Japan,1983.203-215.

3Valmundsson E V, Nau J M.Seismic response of building frames with vertical structural irregularities[J]. Journal of Structural Engineering,1997,123(1):30-41.

4彭俊生.结构动力学、抗震计算与sap2000应用[M].成都:西南交通大学出版社,2007.158-159.

5JGJ 3—2010 高层建筑混凝土结构技术规程[S].北京: 中国建筑工业出版社,2011.

6杨溥,李英民.结构时程分析法输入地震波的选择控制指标[J].土木工程学报,2000,33(6):33-37.

Seimic Response Analysis of an S-type Frame-tube Structure of Vertical Irregularity

SHE Zhaozhao1，LEI Qingguan1,2

(1. Anhui Jianzhu University, Hefei 230601,China; 2. Hefei University of Technology, Hefei 230009,China)

Abstract:The modal analysis of a frame-tube structure of vertical irregularity was made with SAP2000 to analyze the dynamic characteristics of the structure. Furthermore, by using both seismic response spectrum analysis and time history analysis, the seismic behavior and performance of the structures are obtained. The results should be provided reference for the design.

Key words:vertical irregularity; seismic response spectrum analysis; time history analysis; seismic behavior

中图分类号：TU411.01

文献标识码：A

文章编号：2095-8382(2015)05-007-05

DOI：10.11921/j.issn.2095-8382.20150502

作者简介：佘钊钊(1987-)，男，硕士生，主要研究方向为工程抗震。

基金项目：安徽省高等学校自然科学研究重大项目(KJ2014ZD07)

收稿日期：2015-05-14