高港枢纽二线船闸地连墙板桩结构整体数值模拟

钱祖宾，马志华，江守燕，杜成斌，张福贵，刘建龙

(1．江苏省水利勘测设计研究院有限公司，江苏扬州 225009;2．江苏省水利工程建设局，江苏南京 210029;3．河海大学力学与材料学院，江苏南京 210098)

随着江苏沿海大开发、南水北调和淮河入海隧道等工程的建设，许多水利工程和沿海港口工程建设在软土地基上。板桩墙中的地下连续墙可避免施工时大量开挖，可以实现挡土和防渗等临时维护功能，还可以用作永久承重基础结构，特别适宜在土基上构建，其施工噪音小、震动小、场地小，被广泛应用于各种水利(港工)工程中［1］。然而，与这种实践发展不相适应的是，关于板桩墙的计算问题，到目前为止还没有一个大家公认的完善的理论方法或计算模型，原因是多方面的，主要是板桩墙受力和变形情况比较复杂，影响墙土相互作用的因素很多，有些因素对计算模型的影响尚未清楚，加上计算手段的限制，使得有些模型和方法难以在工程上应用。现行规范［2］给出了墙体、桩体施工的一些控制性标准，但对于工程设计的一些设计参数，如土压力分布及取值、拉杆设计等，仍无章可循，现有设计计算已经超出板桩结构设计规范限定范围，一些参数主要借助于土工离心模型试验［3-6］，而离心模型试验存在一定的比尺和边界效应，同时实际工程的受力状态极其复杂，其应用也受到较大的限制。

地连墙墙体的变位程度直接关系到工程的安全及结构内力的计算方法，拉杆内力与墙体变位有着直接的关系，对墙体弯矩有着重要的影响，国内已有多个工程因地连墙结构出现裂缝发生渗漏的实例，如天津港南疆焦炭泊位卸车坑施工过程中地连墙结构槽段连接处出现渗漏［7］，南通惠生船坞工程坞室开挖在完成井点拆除后发现地连墙接头位置衬砌墙上有少量纵向裂缝并有渗水现象。当前实际工程中，对工程结构实际工作性态的掌握主要依赖现场原型观测，不仅成本很高，而且有时会严重影响施工进度。数值方法如有限元法的发展为工程设计和施工提供了有益的指导，国内外大量研究成果表明，运用数值仿真技术可以揭示工程结构在施工期和使用期的真实工作性态，在评价工程结构安全性方面发挥了不可估量的作用。

本文以建设中的泰州引江河高港枢纽二线船闸工程为分析对象，基于ABAQUS商业有限元软件建立船闸地连墙板桩结构整体分析的有限元模型，预测锚碇桩、地连墙的变形性态以及拉杆在施工期不同阶段的内力状态。

1 有限元计算模型

泰州引江河第二期工程高港枢纽二线船闸位于一线船闸西侧，其顺水流向中心线距一线船闸70 m，上闸首的上游边缘与一线船闸闸首的上游边缘齐平。船闸尺寸为230 m×23 m×4 m。根据现行标准［8］，结合本工程的作用及其发生意外事故后的危害程度，船闸下闸首及下游引航道西堤直接关系到长江防洪，为1级水工建筑物，船闸上闸首及闸室为2级水工建筑物，上游引航道为3级水工建筑物，临时工程为5级水工建筑物。上、下闸首均采用钢筋混凝土整体坞式结构，底板顺水流向长29 m、宽53.8 m，底板底高程均为－8.1 m。上闸首设净宽6 m、跨度25 m的公路桥，桥下净空为7 m，荷载标准为公路Ⅱ级。闸室采用透水底板，底面高程－4.5 m，闸室墙采用拉锚地连墙结构，墙后填土高程6.0 m。闸首采用PC预制桩基础，上、下闸首底板下采用地下连续墙防渗地连墙围封。上、下游东西侧导航墙均为拉锚地连墙结构。上、下游引航道底宽均为63.5 m，与一线船闸河底相连，一、二线船闸引航道总底宽为123.5 m。导航墙有效长度均为60 m，引航道上下游20m以内护底为厚60cm的钢筋混凝土护坦，20 m以外120 m以内为20 cm厚现浇混凝土护底。上游引航道河底高程为－4.0 m，平台高程4.0 m，堤顶高程8.5m(考虑弃土堆高)。下游引航道河底高程为－4.5 m，之外为－4.0 m，平台高程为6.0m，堤顶高程为9.0 m。高程－4.0～6.0 m河段为直立式拉锚地连墙结构，引航道总长1235 m。

图1为泰州引江河高港枢纽二线船闸工程典型的锚碇桩-拉杆-地连墙结构体系，据此建立锚碇桩-拉杆-地连墙-土体的有限元整体分析模型。图2为二维有限元分析网格，锚碇桩、地连墙、土体的单元类型均为平面四节点等参元，拉杆的单元类型为平面两节点杆单元。锚碇桩为圆形截面，直径为1.2 m，钢拉杆直径为70 cm。采用平面应变模型进行分析，厚度选取为1根拉杆的影响厚度，约为1.5m(19.5m内共布置13根拉杆)。选取的坐标系x方向垂直闸室，由左侧指向右侧，y方向正向竖直向上。二维整体分析模型共有9065个节点，8748个单元。

2 本构模型及计算参数

图1 锚碇桩-拉杆-地连墙结构体系 (单位:m)

2．1 材料本构模型

数值计算中，对于地连墙、井字梁、锚碇桩以及拉杆采用线弹性本构模型进行计算，参照现行规范［9］拟定材料参数，如表1所示。二维计算时，采用刚度等效的原则对锚碇桩的弹性模量进行相应的折减，折减后弹模为5.94 GPa。

图2 二维有限元计算网格

表1 构件的线弹性材料参数

土体本构模型采用线弹性本构模型时，计算结果与实际情况差距很大，不符合地连墙板桩结构的变形规律;采用Mohr-Coulomb和Drucker-Prager弹塑性本构模型时，由于模型还包括地连墙和土体之间的接触非线性问题，使得计算难以收敛;经过反复数值试验测试，最终采用邓肯-张本构模型，此时地连墙板桩结构的变形规律较符合实际，且计算收敛性较好。邓肯-张模型是非线性弹性模型的典型代表，其弹性模量是应力状态的函数，可以描述土体应力-应变关系的非线性和压硬性。该模型对加荷和卸荷的土体分别采用不同的模量，可以在一定程度上反映土体变形的弹塑性。虽然邓肯-张模型不能描述土体的剪胀性和剪缩性，但该模型具有模型参数少、物理概念明确、确定计算参数所需的试验简单易行等优点，因此在土体的应力-变形分析中得到了广泛的应用。当前ABAQUS软件的材料库尚缺少邓肯-张本构模型，为适应工程分析的需要，江守燕等［10-11］基于ABAQUS平台利用UMAT子程序接口对邓肯-张材料本构模型进行了二次开发。

加载时，邓肯-张E-v模型的切线模量为

式中:Et为切线模量;k、n为弹性模量中的无因次系数;Pa为大气压力;σ3为小主应力;Rf为破坏比;s为应力水平;c、φ为有效应力强度参数;σ1为大主应力。

图10(a)(b)分别给出了动态初始压溃应力和动态应变硬化参数随泡沫铝相对密度的变化。我们采用如下幂函数形式分别进行拟合:

如单元处于卸荷或再加荷状态，式(1)可改用回弹模量表示:

切线泊松比为

式中:Eur为回弹模量;G、F、D为侧向变形系数;kur为卸荷比。上述参数可由土料的静三轴试验得到，本文参照其他工程类似土体拟定，ρ=1900 kg/m3，k、n分别为 398.3、0.84，Rf=0.78，c= 12000 Pa，φ =21.0°，G、F、D 分别为0.406、0.12、3.74，kur=2.1。

2．2 接触本构模型

地连墙与土体之间设置接触，采用点面接触模型，其接触模型的本构关系［12］为

式中:c为初始接触间距;h为接触面之间的相对位移(以嵌入为正);p为接触点对上的接触压力;p0为特征接触力，见图3。

地连墙-土体之间的接触本构模型

当h≤－c时，接触面处于张开状态，接触压力p=0;当h＞－c时，p和接触面相对位移h的关系为指数关系。合理选取c为一微量，并保证p0值足够大，可实现模拟接触面两侧在张开状态时无相互作用，并在接触面闭合时使接触面的挤压力学特性可以光滑过渡;当控制接触面间的嵌入深度为可接受的微量时，与其他接触面模型［13］相比，这种模型在接触面模拟时的收敛性很好，而且精度也较高。计算模型中，c和p0取值分别为0.05 mm和1.0 MPa。

3 模拟计算及结果分析

3．1 施工过程与计算方案

地连墙板桩结构填筑及开挖过程共分21级模拟，见表2。土体填筑及开挖通过ABAQUS的model change功能实现，其中闸室井字梁部分未浇筑前为土体，浇筑后为钢筋混凝土结构，闸室井字梁浇筑前后材料本构模型发生改变，由于ABAQUS无法在一个分析模型中改变同一单元的材料本构模型，需要通过ABAQUS的Import功能实现这一过程，在分析过程之间传递数据［14］。据施工进程设定5个计算工况如表2及图4所示。

表2 地连墙板桩结构填筑及开挖过程模拟工况

图4 地连墙板桩结构计算工况

3．2 计算结果及分析

3．2．1 锚碇桩、地连墙变形情况

表3列出了不同工况下锚碇桩、地连墙水平位移最大值，图5给出了不同工况下锚碇桩水平位移沿高程变化曲线，图6给出了不同工况下地连墙水平位移沿高程变化曲线。图7给出了不同工况下锚碇桩-拉杆-地连墙结构变形。

表3 不同工况下锚碇桩、地连墙水平位移最大值

图5 锚碇桩(L3)水平位移沿高程变化曲线

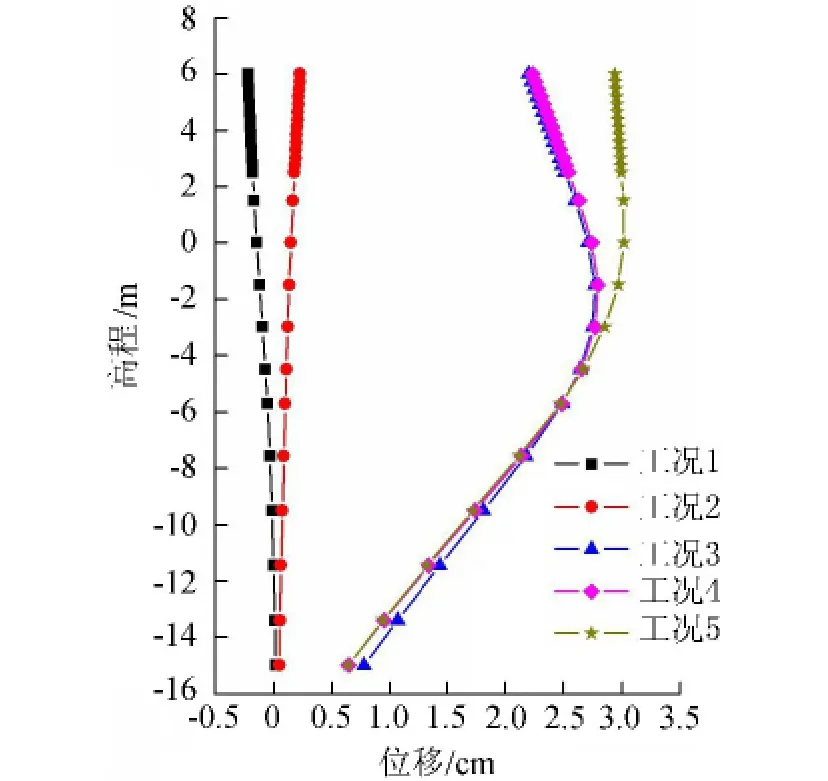
图6 地连墙(L1)水平位移沿高程变化曲线

从计算结果可以看出，在土体填筑和开挖过程中，锚碇桩整体向闸室侧变位，锚碇平台顶部的位移最大，土体填筑和开挖完毕(工况5)后，最大位移值达1.80 cm。闸室土体的开挖过程对锚碇桩的变位影响较大，锚定平台的位移从0.22 cm(工况2)增加到1.62 cm(工况3)，桩基的位移增加到约0.60 cm(工况3);闸室井字梁浇筑完成后，桩基的位移减少到0.57 cm(工况4)。

图7 锚碇桩-拉杆-地连墙结构变形

在土体填筑和开挖过程中，地连墙亦整体向闸室侧变位，墙体位移最大值发生在高程 －2.00～0.00 m之间，土体填筑和开挖完毕(工况5)后，最大位移值达3.02 cm。闸室土体的开挖过程对地连墙的变位影响较大，地连墙的最大位移从0.23 cm(工况2)增加到2.77 cm(工况3)，墙体根部的位移增加到约0.78 cm(工况3);闸室井字梁浇筑完成后，墙体根部的位移减少到0.65 cm(工况4)。

3．2．2 拉杆内力变化情况

图8给出了施工期不同阶段拉杆内力变化曲线。从计算结果可以看出，土体填筑和开挖完毕(工况5)后，拉杆内力达到最大值588.73 kN，闸室土体的开挖过程中拉杆内力迅速增长，从开挖前的35.09 kN增加到开挖后的450.82kN;板桩墙墙后土体的填筑期间，拉杆内力的增长趋于平缓。

图8 1号拉杆内力变化曲线

3．2．3 拉杆对锚碇桩、地连墙变形的影响

拉杆对锚碇桩、地连墙变形的影响如图9所示。从图9可以看出，与有拉杆的情况比较，去掉拉杆后，锚碇桩的水平位移减小，最大值由1.80 cm减小到1.23 cm;而地连墙的水平位移则大幅增加，由3.02cm增加到13.39cm，且地连墙水平位移最大值的位置发生变化，严重影响闸室的稳定性、安全性。

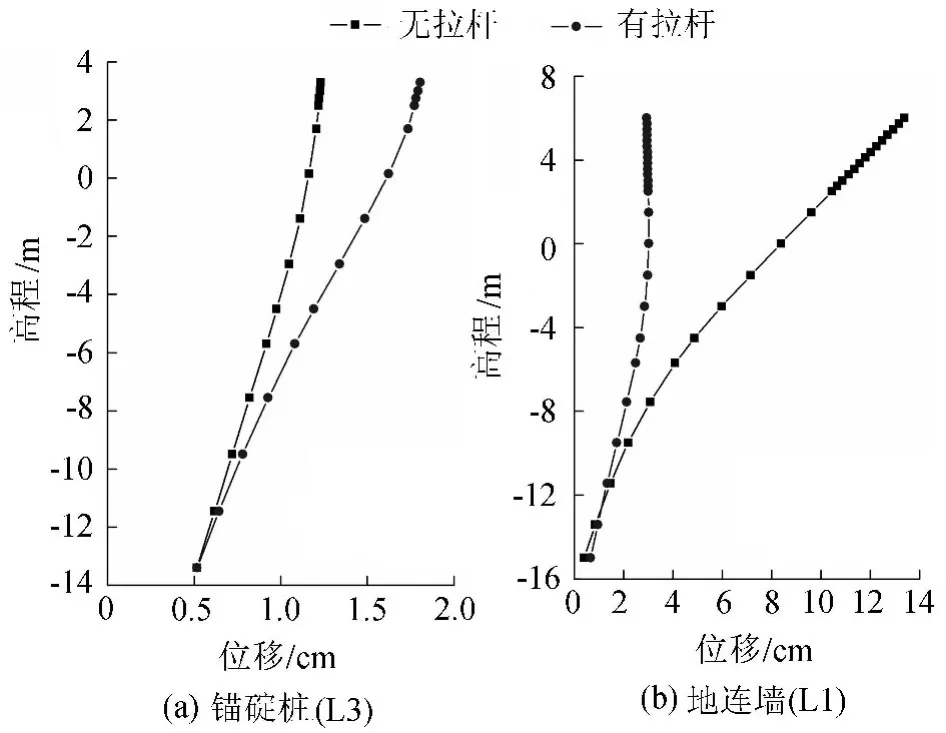
图9 拉杆对锚碇桩、地连墙变形的影响(工况5)

3．2．4 现场实测结果与计算结果的对比

为实时观测施工过程中锚碇桩、地连墙的变位以及拉杆内力在施工不同阶段的变化情况，在锚碇桩、地连墙上预先埋设了测斜管，在拉杆上也预先安装了应变计，提供了大量实测数据，同时也为验证数值计算结果的可靠性提供了很好的依据。

图10给出了现场实测值与有限元计算结果的对比，可以看出，计算得出的锚碇桩、地连墙结构的变位形式与现场实测结果基本一致，计算的锚碇桩最大水平位移为1.80 cm(实测值1.74 cm)，地连墙最大水平位移为2.94 cm(实测值2.94 cm)，与实测值较为接近。计算的拉杆内力最大值为588.73 cm(实测值525.61 cm)，计算得到的施工期不同阶段拉杆内力最大值及其变化趋势与现场实测结果吻合较好，说明计算结果合理准确。

图10 现场实测结果与计算结果的对比(工况5)

4 结语

通过对泰州引江河高港枢纽二线船闸地连墙板桩结构的有限元分析计算，并与现场实测结果对比，结果表明，建立的地连墙板桩结构整体分析模型能够准确地预测施工期不同阶段锚碇桩、地连墙的变位情况以及拉杆的内力情况。研究表明:①在土体填筑和开挖过程中，锚碇桩、地连墙整体向闸室侧变位，闸室土体的开挖过程对锚碇桩、地连墙变位的扰动较大;②闸室土体的开挖过程，是拉杆内力的一个迅速增长期，而土体的填筑对拉杆内力的影响相对较小一些;③拉杆对锚碇桩、地连墙变形的影响较大，在没有拉杆的情况下，锚碇桩的水平位移减小，而地连墙的水平位移大幅增加，且地连墙水平位移最大值的位置发生变化，这会严重影响闸室的稳定性。

［1］刘永绣．板桩和地下墙码头的设计理论和方法［M］．北京:人民交通出版社，2006．

［2］JTS167—3—2009 板桩码头设计与施工规范［S］．

［3］张宏垚．大变位板桩墙结构的数值模拟与结构特性分析［D］．天津:天津大学，2009．

［4］周广柱，徐伟，陈宇．格形地连墙与软土相互作用的离心试验研究［J］．岩土力学，2011，32(增刊 1):134-252．(ZHOU Guangzhu，XU Wei，CHEN Yu．Centrifugal model test study of interaction of griddingconcrete retaining wall and soft soil［J］．Rock and Soil Mechanics，2011，32(Sup1):134-252．(in Chinese))

［5］徐光明，蔡正银，曾友金，等．一种新型板桩码头结构的离心模拟［J］．岩土力学，2010，31(增刊 1):48-52．(XU Guangming，CAI Zhengyin，ZENG Youjin，et al．Centrifuge modeling for an innovative sheet-pile bulkhead of diaphragm［J］．Rock and Soil Mechanics，2010，31(Sup1):48-52．(in Chinese))

［6］李士林，徐光明．单锚板桩结构码头离心模型试验研究［J］．水利水运工程学报，2008(1):67-72．(LI Shilin，XU Guangming．Centrifuge modeling tests for sheet-pile bulkhead anchored by single layer of tie-rods［J］．Hydroscience and Engineering，2008(1):67-72．(in Chinese))

［7］周春松．地下连续墙技术在天津港应用的研究［D］．天津:天津大学，2004．

［8］SL252—2000 水利水电工程等级划分及洪水标准［S］．

［9］SL191—2008 水工混凝土结构设计规范［S］．

［10］江守燕，谢庆明，杜成斌．基于ABAQUS平台邓肯-张EB和 E-v模型开发［J］．河海大学学报:自然科学版，2011，39(1):61-65．(JIANG Shouyan，XIE Qingming，DU Chengbin．Development of program of Duncan-Chang E-B and E-v models based on ABAQUS［J］．Journal of Hohai University:Natural Sciences，2011，39(1):61-65．(in Chinese))

［11］江守燕，谢庆明，杜成斌，等．混凝土心墙堆石坝加固施工模拟［J］．水利水电科技进展，2011，31(2):57-62．(JIANG Shouyan，XIE Qingming，DU Chengbin，et al．Simulation of reinforcing construction of concrete core wall rock-fill dams［J］．Advances in Science and Technology of Water Resources，2011，31(2):57-62．(in Chinese))

［12］江守燕，杜成斌，陈灯红．水电站分缝重力拱坝地震响应分析［J］．河海大学学报:自然科学版，2010，38(3):308-312．(JIANG Shouyan， DU Chengbin， CHEN Denghong．Seismic response analysis of arch dam with key slots occlusion ［J］．Journal of Hohai University:Natural Sciences，2010，38(3):308-312．(in Chinese))

［13］郭海柱，张庆贺．土与结构接触面模型的对比研究［J］．地下空间与工程学报，2009，5(6):1145-1150．(GUO Haizhu，ZHANG Qinghe．A comparison study on the interface model between soil and structure［J］．Chinese Journal of Underground Space and Engineering，2009，5(6):1145-1150．(in Chinese))

［14］曹金凤，石亦平．ABAQUS有限元分析常见问题解答［M］．北京:机械工业出版社，2009:214-217．