非光滑无约束优化次梯度法

□张玉凤

（广西大学 数学与信息科学学院，广西 南宁 530004）

非光滑无约束优化次梯度法

□张玉凤

（广西大学 数学与信息科学学院，广西 南宁 530004）

次梯度法是求解非光滑优化问题的一类经典算法, 也是解决大规模问题的有效方法. 它在经济学、力学、工程和最优控制等许多实际问题中有着广泛应用. 本文概述了经典次梯度法的来源、算法基本框架及进一步的改进方法, 为次梯度方法的进一步研究提供参考.

非光滑优化；次梯度法；椭球法；变尺度

1 引言

本文考虑求解如下形式的非光滑无约束优化问题

其中 f:Rn→R为凸函数，但不一定可微，即函数在某些点没有通常意义下的导数(梯度). 因此，需要对梯度的概念进行推广，引入 f 在 x处的次微分：

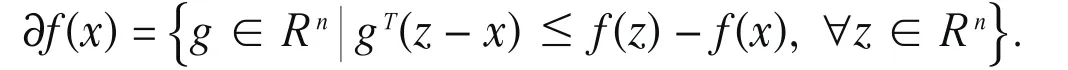
集合∂f(x)中的元素称为 f 在 x处的次梯度. 在算法设计时，通常假设对任意给定的x，能计算出函数值 f(x)及任意一个次梯度g∈∂f(x). 类似于光滑情形，有如下最优性条件(见文[1])：x*是问题(1)的最优解，当且仅当0∈∂f(x*).然而，直接用次梯度法取代光滑优化算法中的梯度求解问题(1)，也是行不通的，原因大致归结为以下三点：(a)终止条件不再适用. 对于光滑无约束优化问题，梯度存在且连续，并且在极小点处梯度为零. 由此可知当迭代点充分靠近最优解时，梯度的范数小于一个充分小量，而对于非光滑优化问题，则没有类似的结果.(b)负次梯度方向不再是下降方向. 对于光滑优化问题，负梯度方向总是下降方向. 而对于非光滑优化问题，并非所有的负次梯度方向都是下降方向. 实际计算表明，由于非光滑优化问题中函数的数学性态较差，许多不使用导数的直接搜索方法也难以对其求解；(c)对于非光滑优化问题，存在“锯齿”现象. 在这种情况下，如用精确搜索的最速下降法求解非光滑优化问题时，可能会收敛到非最优解. 因此，对于求解非光滑优化问题必须建立新的理论及方法.

众所周知，次梯度法[1]是求解非光滑优化问题(1)最经典的方法，其基本思想是用次梯度代替梯度推广光滑优化的方法. 次梯度法结构简单，计算量小，虽然在求解非光滑优化问题方面仍存在缺点，但它是求解非光滑优化问题的基础，也是解决大规模非光滑优化问题的有效算法. 次梯度法简单的算法结构，引起众多学者的关注[2～6]，并被广泛应用于求解各类实际问题[7-10]. 尽管如此，但如何构造一个目标函数的下降方向以及保证算法的快速收敛性仍是研究次梯度算法所面临的难题. 本文将重点介绍非光滑优化问题经典次梯度算法的基本框架及改进方法.

2 经典次梯度法

在光滑优化问题中，通过计算迭代点处的梯度、投影梯度、共轭梯度等容易获得目标函数的下降方向. 但在非光滑优化中，由于目标函数不可微导致在某些点处没有通常意义下的梯度，故许多基于梯度理论的算法失效. 为此，N.Z.Shor[11]首次提出使用次梯度代替梯度的次梯度法，进而将光滑优化中基于梯度的方法推广到求解非光滑优化问题. 下面给出求解问题(1)的次梯度法的基本框架，见文[12].

算法1（经典次梯度法）

步骤0 选取初始点x0及满足一定条件的步长序列{tk}，令k=0；

步骤1 计算gk∈∂f(xk)，若gk=0，则停止；否则转步骤2；

步骤2 令xk+1=xk-tkgk，k=k+1，返回步骤1.

由算法1可知，一方面，经典次梯度法结构简单，在每一个迭代点处只需计算目标函数的一个次梯度即可. 另一方面，次梯度法不需要线搜索，步长事先给定，无需求解不等式，降低了计算量. 在以下三种情况下，算法产生的迭代点列均可收敛到最优解x*，见文[13].

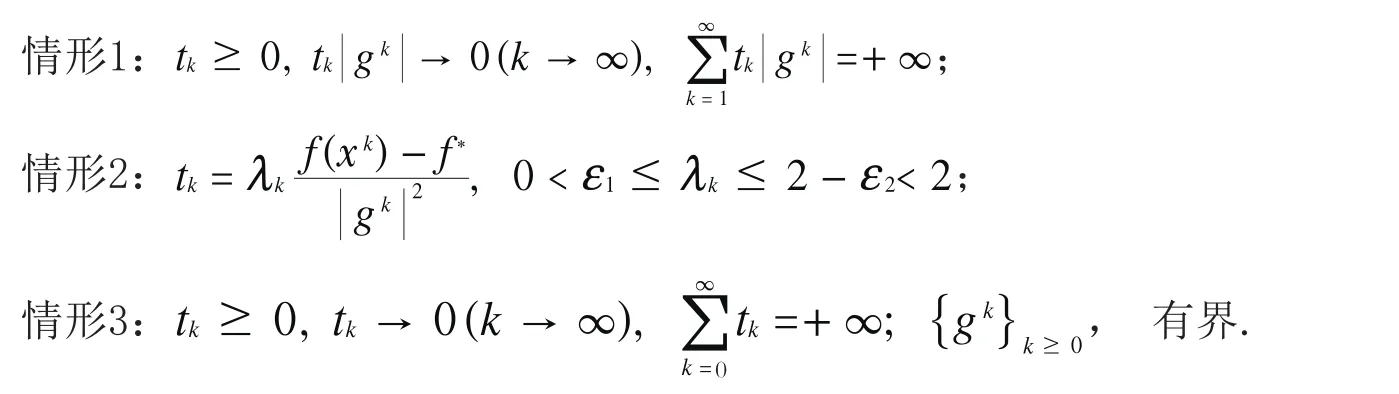
其中情形2假设函数的最优值 f*已知. 不同的步长策略对算法的收敛性有不同的影响，当步长序列选取得当时，可避免锯齿现象，获得好的收敛性.另外，通过改变算法的搜索方向也可提高算法的收敛速率. 下面介绍两种从不同角度出发改进搜索方向的次梯度法.

3 椭球次梯度法

经典次梯度方法的搜索方向直接利用负次梯度.在光滑优化算法中，最速下降法中相邻两方向的梯度正交，在正交方向外搜索最优解x*效果非常差.在非光滑优化问题中为了加快收敛，充分利用前面迭代点的次梯度信息，让相邻两个搜索方向尽量正交.通过引入线性算子Hk减小gk+1中与gk共线的分量，得到在迭代点xk处的搜索方向

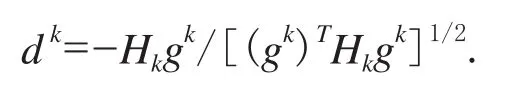
算法2（椭球次梯度法）

步骤0 选取初始点x0，初始矩阵H0=α0I，初始参数α0，β0，t0＞0 ，令k=0；

步骤1 计算gk∈∂f(xk)，若gk=0则停止；否则转步骤2；

步骤2 计算搜索方向dk=-Hkgk/[(gk)THkgk]1/2；

步骤3 令 xk+1=xk-tkdk，用合适的方式更新参数αk，βk，tk，按下式更新Hk

令 k:=k+1，转步骤1.

按下列方式选取参数，会获得较好的收敛结果.

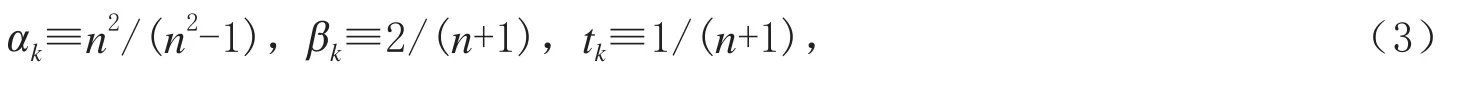
其中，n为空间维数.

定理1[12]设x*为最优解，且满足|x0-x*|2≤α0，则存在M＞0，q＜1，使得由算法2产生的迭代点列{xk}满足

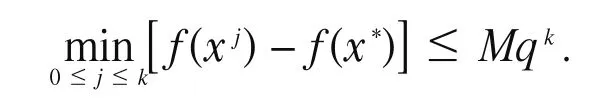
定理1说明{f(xk)} 的一个子序列R-线性收敛到f(x*).

4 变尺度次梯度法

变尺度次梯度法的主要思想与光滑优化的变尺度方法类似，即为得到更好的收敛性，变换原坐标空间，特别是当次梯度方向与指向最优解的方向几乎垂直时，次梯度法的收敛速度很慢.即使改变搜索步长也不会有所改善，在这种情况下，可以通过变换原空间坐标以修正次梯度方向.下面介绍一个变尺度次梯度算法，其迭代点列的更新公式为

其中，tk＞0为搜索步长，Bk∈Rn×n是可逆矩阵，其代表坐标空间的一个线性变换.在线性变换后次梯度有一个重要的性质：线性变换将原空间中 f 的次梯度映射成变换后空间中某个函数的次梯度.

具体地，令y=B-1x，x∈Rn，使得 y-空间为变换后的空间.设g为函数 f 在点处的一个次梯度.在y-空间中，考虑如下函数F

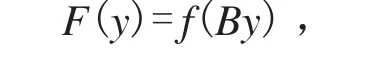
由于 f 是凸函数，故F亦为凸函数.此外，对向量BTg及任意的y∈Rn，有

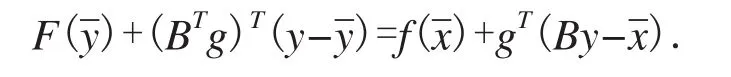
因此，BTg为F在处的次梯度.利用次梯度的这个性质，以及适当的线性变换，可以确保迭代点xk与最优解集之间的距离是有界的.文[11][14]提供了变换矩阵Bk的一种更新公式

其中，初始矩阵B0∈Rn×n非奇异，特别的可取B0=I.线性变换

上述(4)-(7)完成了坐标空间的转化，详见[15].

5 小结

本文介绍了求解非光滑优化问题经典次梯度法的起源、算法基本框架及进一步的改进方法.次梯度法的主要优点是算法结构简单，可求解大规模优化问题.但由于它不能使用梯度，因此在将解决光滑优化问题的梯度算法推广过来时会丢失很多好的性质，使得收敛速度较慢.次梯度法的收敛速度依赖于搜索方向的构造及步长序列的选取.因此，如何借鉴光滑优化方法思想，构造收敛速度快的搜索方向，确定搜索步长序列是次梯度法研究的难点和热点. ■

[1]Shor N Z, Kiwiel K C, Ruszcayǹski A. Minimization methods for nondifferentiable functions [J]. Springer Series in Computational Mathematics, 1985, 3.

[2]韩继业，姚恩瑜.对既约次梯度法的改进[J].应用数学学报，1984，7(1): 101-108.

[3]谭亚，庄建南.非光滑约束问题的既约次梯度法[J].高等学校计算数学学报，2000，22(4)：325-330.

[4]Kiwiel K C. An aggregate subgradient method for nonsmooth convex minimization[J]. Mathematical Programming, 1983, 27(3): 320-341.

[5]Kim S, Koh S. On Poljak's improved subgradient method [J]. Journal of Optimization Theory and Applications, 1988, 57(2): 355-360.

[6]Kiwiel K C. Methods of descent for nondifferentiable optimization[M]. Springer Lecture Notes in Mathematics, 1985.

[7]邓艾东，包永强，赵力.基于能量衰减模型的转子碰摩声发射源次梯度投影定位方法[J].机械工程学报, 2010，46(9)：66-72.

[8]梁瑞宇，邹采荣,王青云等.基于自适应次梯度投影算法的压缩感知信号重构[J].信号处理，2010，26(12)：1883-1889.

[9]曹绪龙，同登科，王瑞和.考虑二次梯度项影响的非线性不稳定渗流问题的精确解[J].应用数学和力学，2004，25(1)：93-99.

[10]Cavalcante R L G, Yamada I. Multiaccess interference suppression in orthogonal spacetime block coded MIMO systems by adaptive projected subgradient method[J]. Signal Processing, IEEE Transactions on, 2008, 56(3): 1028-1042.

[11]Shor N Z. Minimization methods for nondifferentiable functions[J]. Springer series in computati-on al mathematics, 1985, 3.

[12]Nemhauser G L, Kan A H, Todd M J. Handbooks in operations research and management scienceoptimization[M], 1989.

[13]Kim S, Ahn H. Convergence of a generalized subgradient method for nondifferentiable convex optimization[J]. Mathematical Programming, 1991, 50(1-3): 75-80.

[14]Shor N Z. Nondifferentiable optimization and polynomial problems[J]. Nonconvex Optimization and Its Applications, 1998, 24.

[15]Nedic A. Subgradient methods for convex minimization, Ph.D thesis, MIT, 2002.

【责任编辑 谢文海】

Subgradient Methods for Nonsmooth Unconstrained Optimization

ZHANG Yu-Feng
(School of Mathematics and Information Science, Guangxi University, Nanning, Guangxi, 530004)

Subgradient methods are classical methods for solving nonsmooth optimization problems, especially for large-scale problems. They are widely used in many practical applications, such as economics, mechanics, engineering and optimal control. In this paper, we describe the source of classical subgradient methods, the basic framework and further improvements, which provide the basis for further study.

nonsmooth optimization; subgradient; ellipsoid methods; variable metric

O224

A

1004-4671（2015）02-0027-04

2015-03-31

广西自然科学基金创新研究团队（2014GXNSFFA118001）。

张玉凤（1987～），女，河北河间人，广西大学数学与信息科学学院研究生。主要研究方向：最优化理论与算法。