空气涡轮火箭发动机热力循环特性分析

李文龙,郭海波,南向谊

（西安航天动力研究所，陕西 西安710100）

0 引言

空气涡轮火箭 （Air Turbo Rocket，ATR）发动机是火箭发动机和航空涡轮发动机成熟技术的有机融合，具有比冲高于火箭发动机，推重比大于航空发动机，工作空域和速域宽等优势，技术难度适中，是未来可应用于高动态临近空间飞行器、远程空射武器以及天地往返运载器的新型吸气式组合动力[1-2]。

ATR发动机热力循环最重要的特点就在于其涡轮流路分离设计，可采用独立于空气来流的火箭燃气发生器循环方式产生富燃燃气驱动涡轮带动压气机，进气道来流畸变敏感性降低，系统调节规律得以简化，对空气来流进行预冷却或与冲压发动机集成为多模态后可进一步拓宽发动机的工作空域和速域[3-4]。

20世纪80至90年代，美国Aerojet公司、美军导弹司令部（U.S.Army Missile Command,MICOM）以及CFD研究公司 （CFD Research Corporation）在开展固体推进剂 ATR（SPATR）和肼单组元ATR发动机技术研究过程中，建立了ATR发动机设计点和非设计点状态数学模型[5-7]，考察了ATR发动机的调节规律和部件参数匹配规律[1-2,8-9]。近年来，国内的屠秋野分析了SPATR发动机的气动热力循环和非设计点性能[10-13]；莫然开展了涡轮增压固体冲压发动机的热力循环分析[14]；潘宏亮建立了液体推进剂ATR和加力式ATR发动机的性能分析模型[15-16]，进一步分析了发动机高度特性和速度特性。以上研究大多着力于发动机性能参数分析，多因素耦合作用下的液体推进剂ATR系统热力循环特性分析较少。此外，有关ATR热力循环的优势及其具体应用模式得到了持续论证和分析。

本文采用热力学第一定律分析法分析液体推进剂ATR热力循环过程及其能量转换关系，得出热力循环性能参数，探讨ATR热力循环的优势及特点，进而分析地面静态和飞行状态下热力学特征参数对发动机热力循环特性的影响规律，旨在为ATR发动机系统参数优化提供一定的理论支撑。

1 ATR发动机理想热力循环

1.1 特征截面及符号

对如图1所示的ATR热力循环特征截面进行说明：0为远前方气流未受扰动状态截面；1为进气道入口截面；2为进气道出口，同时也是压气机进口截面；3为压气机出口截面；4为涡轮入口，同时也是燃气发生器出口截面；5为涡轮出口截面；6为富燃燃气与增压空气的宏观尺度混合截面；7为燃烧室内空气和富燃燃气掺混燃烧结束截面；8为尾喷管喉部截面；9为尾喷管出口截面。

图1 ATR热力循环特征截面Fig.1 Characteristic section of ATR thermodynamic cycle

1.2 理想热力循环过程

首先将ATR动力循环抽象简化为可逆理论循环，在此采用“空气标准假设”[17-18]：假定循环工质是理想气体，且具有与空气相同的热力性质；将燃料定压燃烧过程简化为可逆的定压加热过程，排气过程简化成向低温热源的可逆定压放热过程；忽略膨胀、压缩及混合过程中的熵增等次要因素；高温的内涵富燃燃气与温度相对较低的外涵空气在燃烧室入口处的压力相等或近似相等，在下游发生掺混和燃烧。

将ATR发动机热力循环用一系列基本热力过程来表征，其理想热力循环如图2所示，其中质量 m 的液体推进剂经 0′-2′-4-5-6-7-9-0′完成液体火箭发动机理想循环，单位质量空气经0-2-3-6-7-9-0完成航空燃气涡轮发动机理想循环。

图2 ATR理想热力循环p-v图和h-s图Fig.2 Pressure-specific volume and enthalpy-entropy relation of ideal ATR thermodynamic cycle

理想热力循环中的基本热力过程如下：0′-2′为质量m的液体推进剂在供应系统中的定容增压过程；2′-4为推进剂在发生器中的等压燃烧过程；4-5为燃气在涡轮中的等熵膨胀过程；5-6为质量m燃气在气气掺混过程中的等压放热过程；0-2为单位质量空气在进气道中的等熵压缩过程；2-3为单位质量空气在压气机中的等熵压缩过程；3-6为单位质量空气在气气掺混过程中的等压吸热过程；5-6为混合燃气 (1+m)在燃烧室中的等压燃烧过程；7-9为混合燃气 (1+m)在尾喷管中的等熵膨胀过程；9-0为混合燃气 (1+m)在大气中的等压放热过程。

1.3 理想热力循环性能

热力系统的加热量等于系统焓的增量与多方压缩功之差，图2所示的理想热力循环p-v过程曲线所包围的面积即为理想循环功:

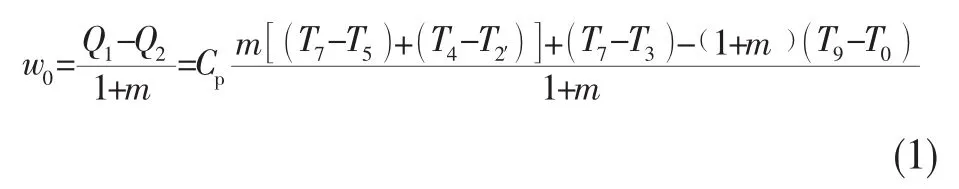
式中：Q1为等压加热过程的总加热量；Q2为等压放热过程的总放热量。

理想循环的热效率定义为系统净加热量与等压加热量之比，即有：

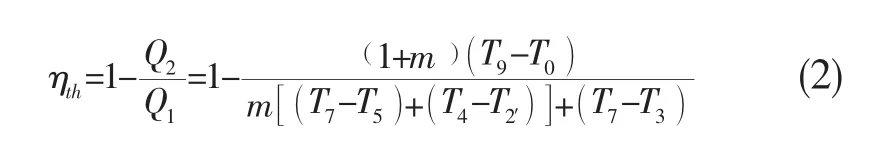
定义5个热力学特征参数如下：发生器温比τgg，燃烧室温比τcc，进气道冲压比πi，压气机压比πc和涡轮落压比πt，即有：

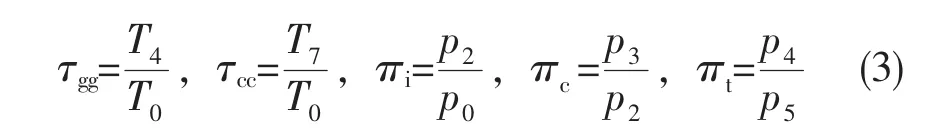
式中τgg和τcc分别为火箭发动机循环和组合循环的最高温度与最低温度之比即循环总增温比。

气体动力循环工质均为理想气体，定压比热容:

式中k为循环工质（空气和燃气）的比热比。

进气道内的等熵压缩过程：

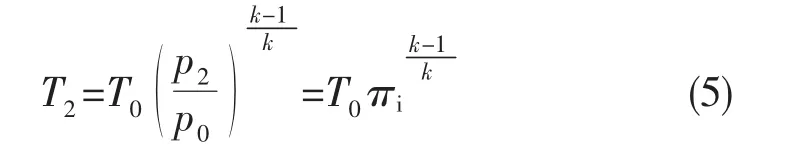
压气机等熵压缩过程：

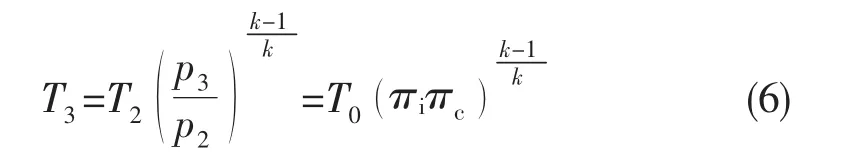
涡轮等熵膨胀过程：

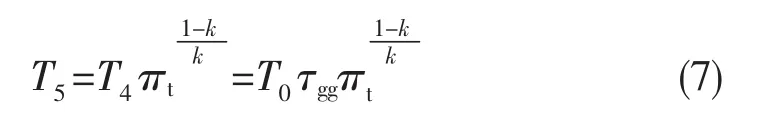
尾喷管中的等熵膨胀过程：

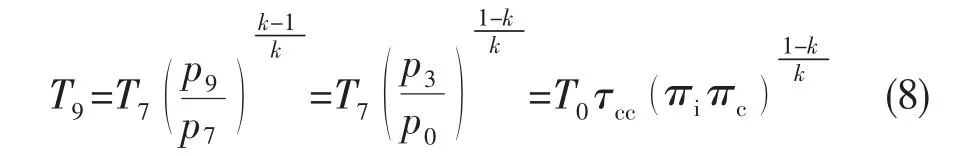
质量m液体推进剂的定容增压过程：

涡轮与压气机功率平衡:

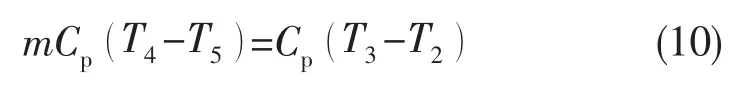
将式 (3)～(6)代入式 (10)，可得理想热力循环中的燃料（液体推进剂）质量:

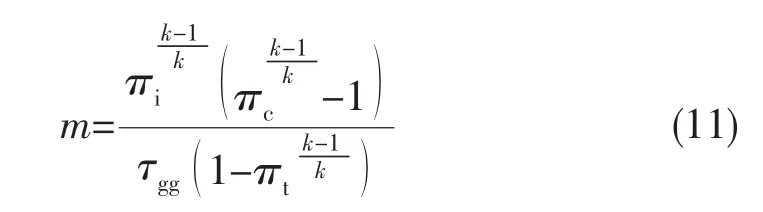
将式 (3)～(11)分别代入式 (1)和 (2)后可得：

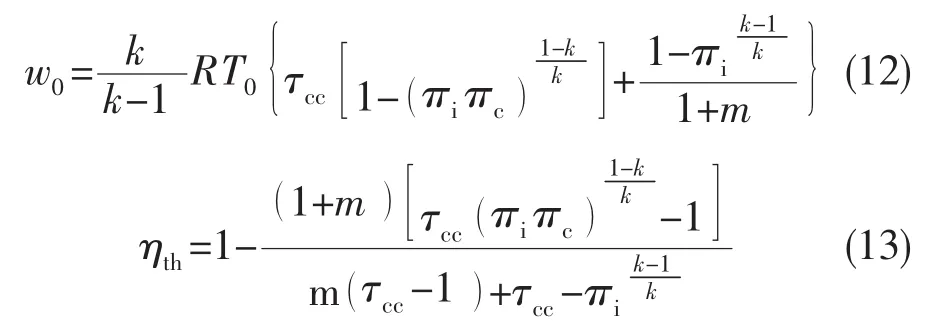
发生器循环工质必须由发动机自身携带，不考虑燃烧室中燃料的二次喷注，定义燃料比冲:

由燃料比冲与理想循环功的关系可知：

式 (12)、式 (13)和式 (15)分别为ATR发动机理想热力循环功、热效率和燃料比冲的一般表达式。热力循环工质一定，ATR理想热力循环性能仅取决于式 (3)所定义的5个热力学特征参数。

2 地面静态热力循环特性

地面静态是指发动机在地面来流马赫数为0的状态。此时，进气道无速度冲压效应，假定πi＝1，联立式 (11)～(13)及式 (15)，可得ATR地面静态理想热力循环的性能参数：

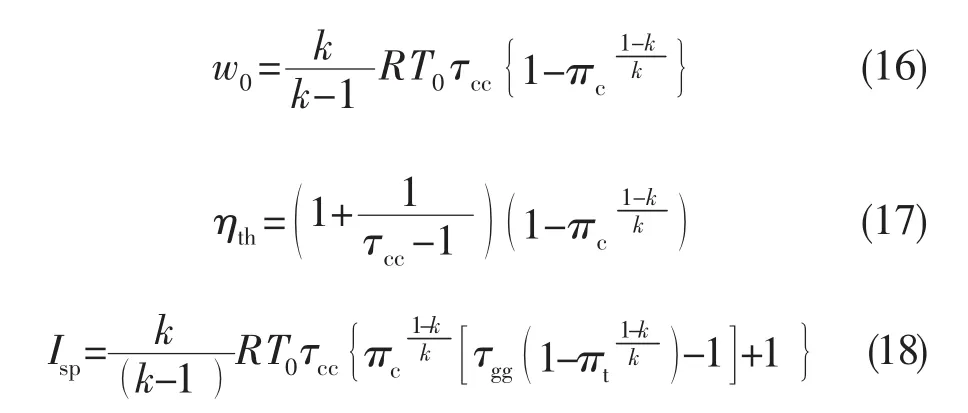
ATR地面静态理想热力循环性能参数与理想布雷顿（Brayton）循环性能参数间的基本关系为：

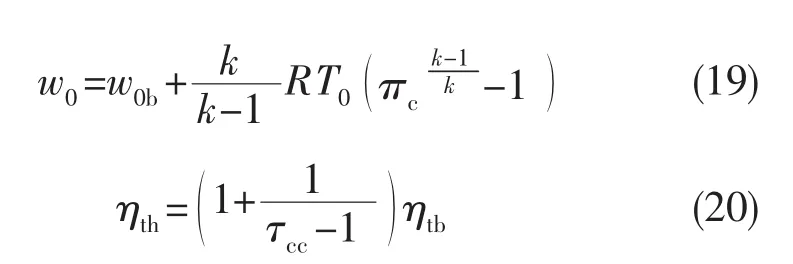
式中w0b和ηth分别为理想布雷顿循环功和热效率。地面静态理想热力循环功和热效率仅是燃烧室温比τcc和压气机压比πc的单调函数。提高燃烧室温比，理想循环功（循环净面积）增大，受发生器等压加热量的限制，理想循环吸热量的增加幅度将小于放热量的增加幅度，从而热效率减小；提高压气机压比，理想循环功增大，涡轮机功率平衡，相当于提高了发生器的等压加热量，热效率增大。

ATR地面静态理想循环功和热效率随τcc和πc的变化规律如图3所示。

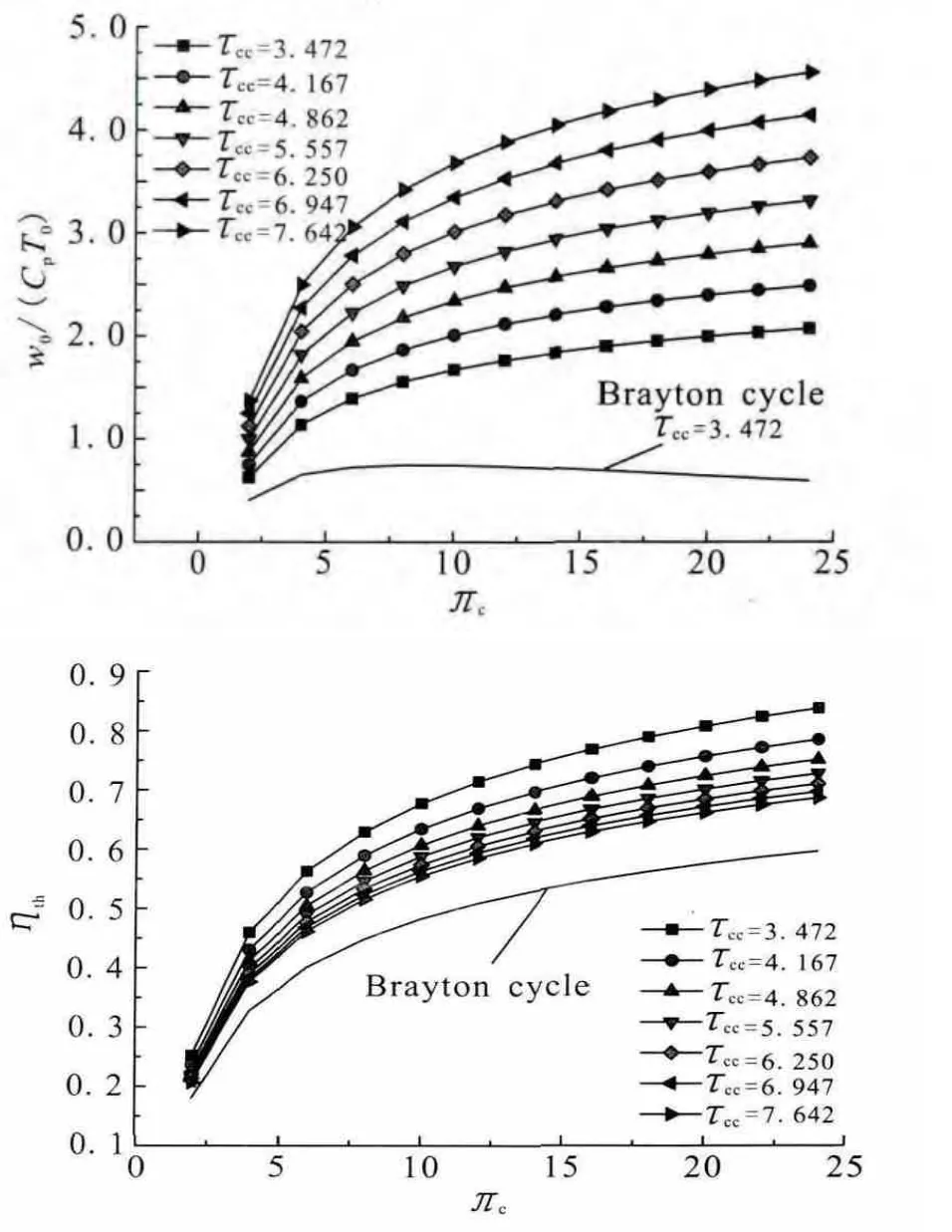
图3 理想循环功和热效率随τcc和πc的变化关系Fig.3 Variation of ideal cycle work and thermal efficiency with combustor temperature ratio and compressor pressure ratio

在相同的燃烧室温比 τcc条件下，ATR理想循环功始终大于布雷顿循环功，两热力循环功的差别随压气机压比τcc的增大而增大。在相同的τcc条件下，ATR理想循环热效率高于布雷顿循环热效率，提高燃烧室温比τcc，理想循环热效率减小并逐渐趋近于布雷顿循环热效率。

由于涡轮的输出功全部用于带动压气机增压，ATR热力循环就是在布雷顿循环基础上增加了一个等压吸热过程，相当于提高了平均吸热温度，因此热力循环功更大，热效率更高。压气机压比一定，则增加的等压吸热量一定，燃烧室温比增大，该等压吸热量占ATR热力循环总吸热量的比重将随之降低，其极限即为布雷顿循环热效率。

地面静态条件下，忽略燃烧室二次喷油，燃料比冲与燃烧室温比和发生器温比成正比；提高涡轮落压比，比冲增大，但增大幅度随涡轮落压比的提高逐渐减小。压气机压比对比冲的影响与发生器温比和涡轮落压比的相对关系有关，定义：

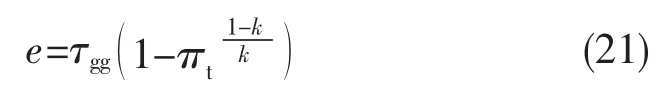
显然，当e＞1时，提高πc，比冲减小；当e=1时，提高πc，比冲不变；当e＜1时，提高πc，比冲增大。假定k=1.4，τgg=4.167，τcc=6.944时，比冲随 πc和 πt的变化关系如图 4所示。 其中，πt＜2.613时，比冲随着πc的提高而增大；πt=2.613时，比冲不随πc变化；πt＞2.613时，比冲随 πc的提高而减小。

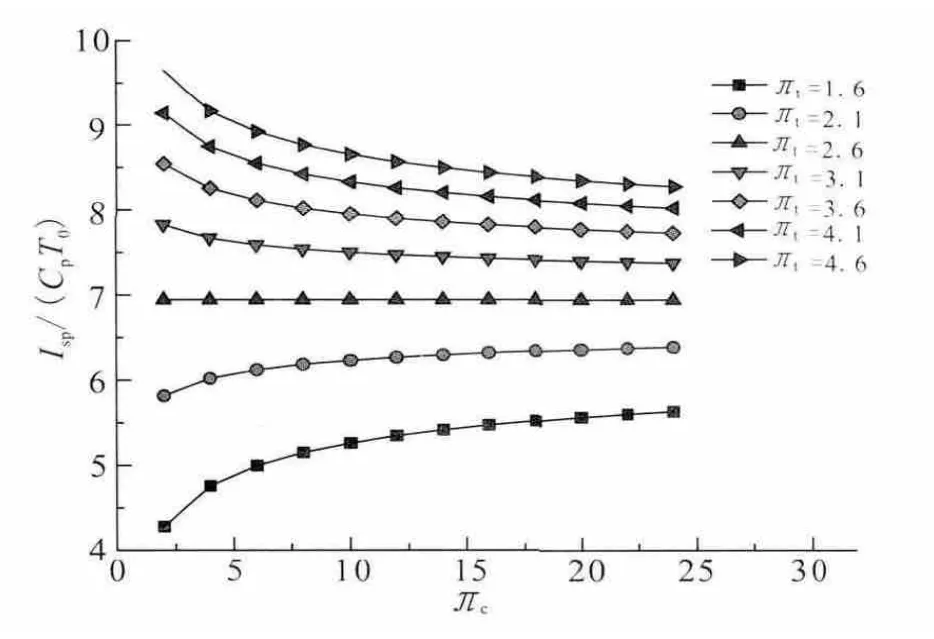
图4 比冲随压气机压比和涡轮压比的变化关系Fig.4 Variation of specific impulse with pressure ratios of compressor and turbine

压气机压比πc增大，理想循环功和发生器的工质流量均随之增大，但m的增大幅度受发生器温比和涡轮落压比的影响。当e＞1时，随着πc增大，m增大幅度大于循环功的增大幅度，因此比冲降低。为获取较高的发动机比冲性能，应尽量选取高的发生器温比和涡轮落压比，大多数条件下e＞1条件都将成立，此时提高πc，热效率和循环功都将增大，但比冲降低。

3 飞行状态热力循环特性

为便于分析不同来流马赫数状态下的ATR理想热力循环特性，分别考察发生器循环工质m趋近于无限小和无限大2个极限工况的循环功和热效率。

1)假设发生器温比和涡轮落压比很大，燃气发生器循环工质m→0，此时理想循环功和热效率可分别改写为：

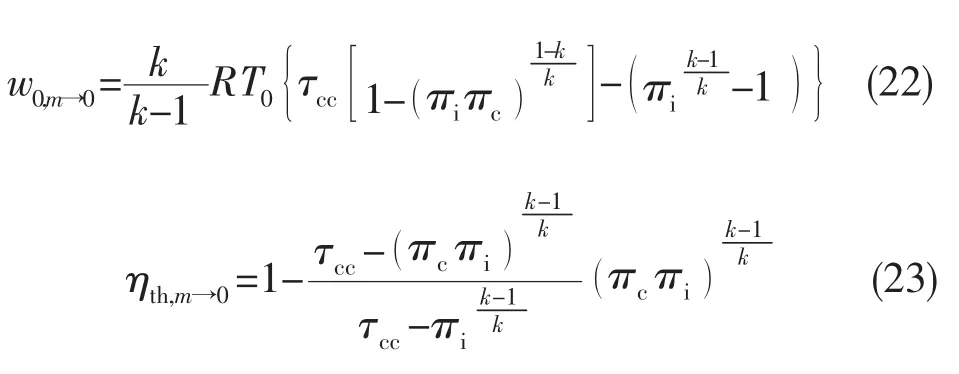
燃烧室温比和压气机压比一定时，理想循环功存在最大值，此时对应的进气道冲压比和飞行马赫数为：

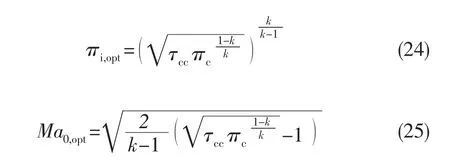
将式 (24)代入式 (22)可得m→0时的最大循环功：

2)假设发生器温比和涡轮落压比很小，燃气发生器工质，循环功和热效率可分别改写为：

在m→∞工况条件下，仍然有ATR循环功和热效率大于布雷顿循环相应值的基本规律。

当m→∞时最大理想循环功为：

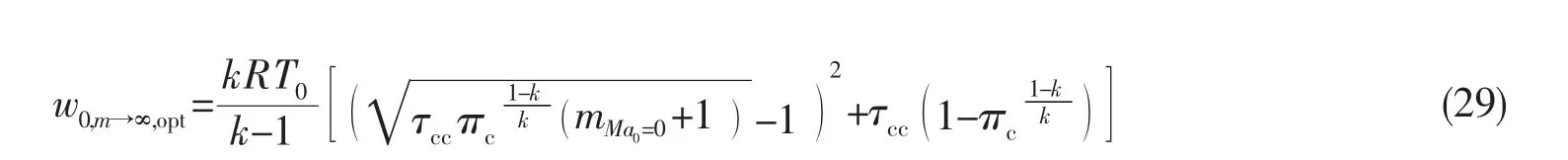
最大燃料比冲为:

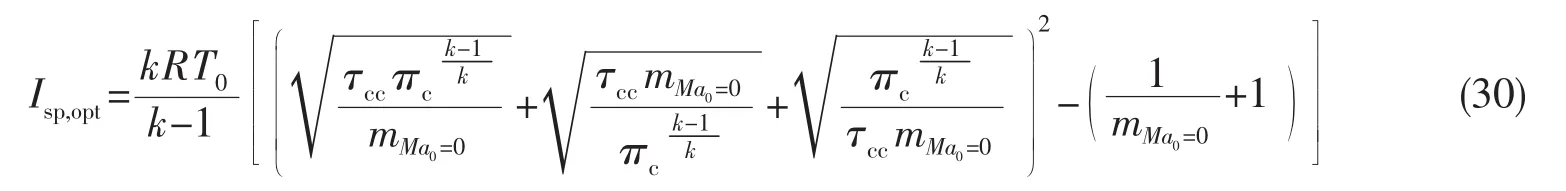
式中mMa0=0为飞行马赫数为0时对应的发生器循环工质流量，其值可表示为：

综上所述，典型飞行状态工况条件下（k=1.4， τcc=6.944， πc=3.0 和 πt=10）， ATR 发动机理想循环热效率、循环功和比冲随飞行马赫数的变化关系如图5所示。其中，燃气发生器温比与发生器循环工质质量m直接相关。在图5中分别绘制出了最大循环功连线和最高燃料比冲连线。

ATR理想循环热效率随飞行马赫数的增大而增大，循环功和比冲随飞行马赫数的变化趋势与发生器循环工质m（以燃气发生器温比表征）相关。随着飞行马赫数增加，理想循环功和比冲先增大后减小，均存在最大值。此外，ATR最大循环功对应的飞行马赫数始终大于最高比冲对应的飞行马赫数。

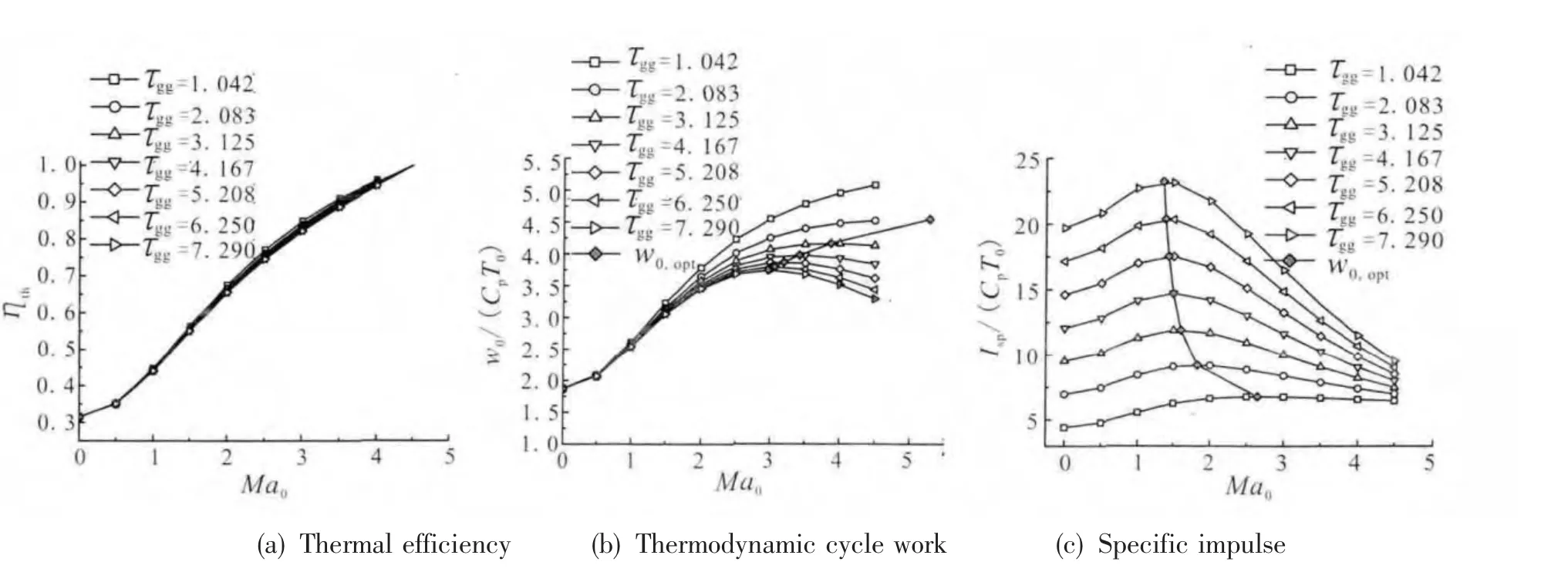
图5 热效率、循环功和比冲随Ma0的变化关系Fig.5 Variation of thermal efficiency,thermodynamic cycle work and specific impulse with Ma0

发生器循环工质m对ATR理想循环热效率的影响较小；理想循环功随m的减小而减小，且其下降幅度逐渐减小并趋于恒定；发动机比冲随m的减小而等比例增加，但最高比冲对应的飞行马赫数不断减小并趋于恒定。

4 结论

本文从热力循环角度分析了地面静态和飞行状态下ATR理想热力循环特性，结果表明：

1)影响ATR发动机热力循环性能的热力学特征参数有：进气道冲压比（来流马赫数）、压气机压比、涡轮落压比、发生器温比和燃烧室温比。在相同的压气机压比条件下，ATR循环功和热效率始终高于布雷顿循环的相应值。

2)地面静态的理想循环功和热效率仅是燃烧室温比和压气机压比的单调函数。提高燃烧室温比，热效率降低、循环功增加；提高压气机压比，热效率和循环功均增加。比冲与燃烧室温比和发生器温比成正比，提高涡轮落压比，比冲增加，但增加幅度逐渐减小，压气机压比对比冲的影响与燃烧室温比和发生器温比相对关系有关。

3)理想循环热效率随飞行马赫数的增大而增大，循环功和比冲随飞行马赫数的增加而先增大后减小，存在最大值，其最大循环功对应的飞行马赫数始终大于最高比冲对应的飞行马赫数。

4)发生器循环工质对热效率的影响较小，但循环功随发生器循环工质的减小而减小，比冲随发生器循环工质的减小而等比例增加。

在ATR发动机系统参数优化过程中，只有压气机压比存在较大选取空间，该热力学特征参数应根据飞行任务剖面要求慎重选取，在保证足够推力的同时尽可能获得高比冲性能。

[1]BOSSARD J A,CHRISTENSEN K L,FEDUN M H.Return of the solid fuel gas generator ATR,AIAA-87-1997[R].USA：AIAA,1987.

[2]CHRISTENSEN K.Air turborocket/vehicle performance comparison[J].Journal of Propulsion and Power,1999,15(5)：706-712.

[3]SATO T,TANATSUGU N,HATTA H,et al.Developent study of the ATREX engine for TSTO space plane,AIAA 2001-1839[R].USA：AIAA,2001.

[4]李成,蔡元虎,屠秋野,等.射流预冷却吸气式涡轮火箭发动机性能模拟[J].推进技术,2011,32(1)：1-4.

[5]CHRISTOPHER A S.A parametric study of a gas-generator airturbo ramjet(ATR),AIAA 86-1681[R].USA：AIAA,1986.

[6]DAVID R H.A Computer program for the design and off-design performance of an air turbo-rocket(ATR)[D].Arlington,US：The University of Texas,1996.

[7]LILLEY J S,HECHT S E,KIRKHAM B C,et al.Experimental evaluation of an air turbo ramjet,AIAA 94-3386[R].USA：AIAA,1994.

[8]CLOUGH J A,LEWIS M J.Component matching for the air turborocket,AIAA 2004-3648[R].USA：AIAA,2004.

[9]BUSSI G,COLASURDO G,PASTRONE D.An analysis of air-turborocket performance[J].Journal of Propulsion and Power,1995,11(5)：950-954.

[10]屠秋野,陈玉春,苏三买,等.固体推进剂吸气式涡轮火箭发动机的建模及特征研究 [J].固体火箭技术,2006,29(5)：317-319.

[11]陈湘,陈玉春,屠秋野,等.固体推进剂空气涡轮火箭发动机的非设计点性能研究[J].固体火箭技术,2008,31(5)：445-448.

[12]屠秋野,丁朝霞,陈玉春,等.固体推进剂吸气式涡轮火箭发动机的气动热力循环分析[J].固体火箭技术,2009,32(1)：53-57.

[13]李成,周正,屠秋野,等.吸气式涡轮冲压发动机性能模拟及验证[J].航空动力学报,2013,28(11)：2562-2566.

[14]莫然,刘佩进,刘洋,等.涡轮增压固体冲压发动机热力循环分析[J].固体火箭技术,2011,34(5)：598-602.

[15]潘宏亮,周鹏.空气涡轮液体火箭发动机建模与仿真研究[J].西北工业大学学报,2009,27(4)：492-498.

[16]潘宏亮,林彬彬,刘洋.加力式空气涡轮火箭发动机特性研究[J].固体火箭技术,2010,33(6)：650-655.

[17]沈维道,蒋智敏,童钧耕.工程热力学[M].北京：高等教育出版社,2001：268-290.

[18]廉筱纯,吴虎.航空发动机原理[M].西安：西北工业大学出版社,2005：122-134.