关于线性型Sylvester的问题注记

周　虎， 强　华， 顾银鲁， 宋桢桢

(银川能源学院 数学教研室，宁夏 银川 750105)



关于线性型Sylvester的问题注记

周虎， 强华， 顾银鲁， 宋桢桢

(银川能源学院 数学教研室，宁夏 银川 750105)

摘要：设正整数a1,a2,a3的最大公约数(a1,a2,a3)=1，证明了3元线性型的Sylvester数存在，给出既定条件中的s(a1,a2,a3)计算公式，并给出既定条件下4元、5元线性型Sylvester数的计算公式.

关键词：线性型；正整数解；Sylvester数；广Sylvester数

1引理

19世纪Sylvester证明了定理[1]：设正整数a1,a2的最大公约数(a1,a2)=1，对于方程

a1x1+a2x2=n，

(1)

当n>a1a2，方程(1)有正整数解，当n=a1a2，方程(1)无正整数解.

本文将用初等方法证明：正整数a1,a2,a3的最大公约数(a1,a2,a3)=1，不定方程

a1x1+a2x2+a3x3=n

(2)

存在与a1,a2,a3有关的整数s(a1,a2,a3)，当n>s(a1,a2,a3)，方程(2)有正整数解，当n=s(a1,a2,a3)，方程(2)无正整数解，称数s(a1,a2,a3)为线性型的Sylvester数，简称s数.给出数s(a1,a2,a3)计算公式，并且在一定条件下4元、5元线性型Sylvester数的计算公式.

如无特别说明，本文中字母表示正整数，将“方程有(无)正整数解”简述为“方程有无解”.

引理1对于不定方程a1x1+a2x2=n，

1)若(a1,a2)=1， 当n>a1a2，方程(1)有正整数解，当n=a1a2，方程(1)无正整数解；

2)若(a1,a2)=δ3，当n≡o(modδ3)，当n>G(a1,a2)=a1a2/δ3，方程(1)有正整数解，当n=G(a1,a2)，方程(1)无正整数解.数G(a1,a2)称为线性a1x1+a2x2的广Sylvester数，简称广s数.

证明由(a1,a2)=δ3，a1=δ3b1，a2=δ3b2，(b1,b2)=1，在条件n≡o(modδ3)下，方程(1)两端同除以δ3，得到

b1x1+b2x2=k.

(3)

由1)知，当k>s(b1,b2)=b1b2，方程(3)有解，当k=s(b1,b2)，方程(3)无解.对于方程(1)而言，当n≡o(modδ3)，当n>G(a1,a2)=δ3b1b2=a1a2/δ3，方程(1)有解，当n=G(a1,a2)，方程(1)无解.

引理2设(a1,a2,a3)=1，不定方程a1x1+a2x2+a3x3=n存在与a1,a2,a3有关的整数s(a1,a2,a3)，当n>s(a1,a2,a3)，方程(2)有正整数解，当n=s(a1,a2,a3)，方程(2)无正整数解.

证明1)设(a1,a2)=δ3，a1=δ3b1，a2=δ3b2，(b1,b2)=1，不定方程(2)化为

b1x1+b2x2=(n-a3x3)/δ3，

(4)

若方程(2)有解，(4)式右端应为正整数，由(a3,δ3)=1，对参变数n，存在整数A1,3，

1≤A1,3≤δ3，

(5)

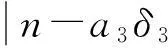
b1x1+b2x2=(n-a3A1,3)/δ3=n3.

(6)

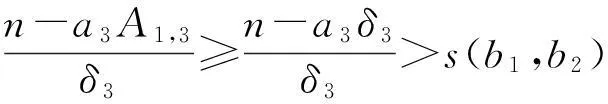
方程(2)有解x1=A1,1,x2=A1,2,x3=A1,3，令

Na(123)=δ3s(b1b2)+a3δ3.

(7)

2)设(a1,a3)=δ2，a1=δ2c1，a3=δ2c3，(c1,c3)=1，方程(2)化为

c1x1+c3x3=(n-a2x2)/δ3.

(8)

用1)中方法得到n>δ2s(c1,c3)+a2δ2.

方程(2)有解x1=A2,1,x2=A2,2,x3=A2,3，其中s(c1,c2)是线性型c1x1+c3x3的s数.令

Na(132)=δ3s(c1,c3)+a2δ2.

(9)

3)设(a2,a3)=δ1，a2=δ1e2，a3=δ1e3，(e1,e3)=1，方程(2)化为

e1x1+e3x3=(n-a1x1)/δ1.

(10)

用1)中方法得到n>δ1s(e1,e3)+a1δ1，方程(2)有解x1=A3,1,x2=A3,2,x3=A3,3，其中s(e1,e2)是线性型e1x2+e3x3的s数.令

Na(231)=δ1s(e2,e3)+a1δ1.

(11)

式(7)，(9)，(11)是正整数，必有最小者，不妨设此3式中最小者为Na(123)，由证明知，当n>Na(123),方程(2)有解，当n=Na(123)代入(2)化简得

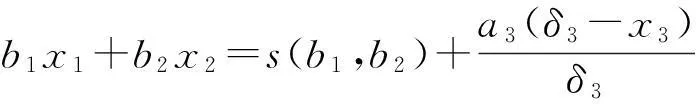
(12)

故，当n=Na(123)，方程(12)无解，从而方程(2)无解.

2定理

定理1设(a1,a2,a3)=1，(a1,a2)=δ3，(a1,a3)=δ2，(a2,a3)=δ1，

a1=t1δ2δ3，a2=t2δ1δ3，a3=t3δ1δ2，

(13)

其中，δi至少有一个大于1(i=1,2,3).

线性模型a1x1+a2x2+a3x3的s数为

1)若t3>max{t1,t2}，

s(a1,a2,a3)=a1a2/δ3+a3δ3；

(14)

2)若t2>max{t1,t3}，

s(a1,a2,a3)=a1a3/δ2+a2δ2；

(15)

3)若t1>max{t2,t3}，

s(a1,a2,a3)=a2a3/δ1+a1δ1.

(16)

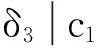
N(123)=δ3[s(b1,b2)+a3]，

(17)

N(132)=δ2[s(c1,c3)+a2]，

(18)

N(231)=δ1[s(e2,e3)+a1]，

(19)

其中s(b1,b2)=b1b2，s(c1,c3)=c1c3，s(e2,e3)=e2e3分别是线性型b1x1+b2x2，c1x1+c3x3，e2x2+e3x3的s数.

若(17)为3式中的最小者，只要不等式组

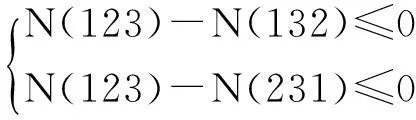
(20)

成立，(20)化简为

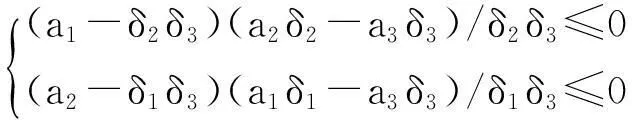
由(13)得a1-δ2δ3≥0，a2-δ1δ3≥0，从而不等式化为

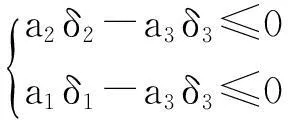
解之，t3≥t2，t3≥t1，即当t3≥max{t2,t1}时，线性型a1x1+a2x2+a3x3的s数

s(a1,a2,a3)=a1a2/δ3+a3δ3.

同法,由不等式组

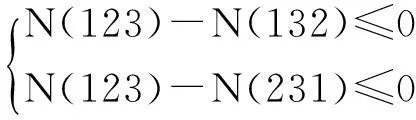
及

推得(15)，(16)式.

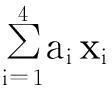
s(a1,a2,a3,a4)=min{N(1234),N(1243),N(1342),N(2341)}，

(21)

其中N(1234)=s(a1,a2,a3)+a4，N(1243)=s(a1,a2,a4)+a3，N(1342)=s(a1,a3,a4)+a2，N(2341)=s(a2,a3,a4)+a1.

证明当(a1,a2,a3)=1，由定理1求得线性型a1x1+a2x2+a3x3的s数s(a1,a2,a3)，限定x4=1，数N(1234)=s(a1,a2,a3)+a4，对于方程

(22)

当n>N(1234)，方程(22)有解，当n=N(1234)，方程(22)无解.

同理，分别限定x3=1，x2=1，x1=1，N(1243)=s(a1,a2,a4)+a3，N(1342)=s(a1,a3,a4)+a2，N(2341)=s(a2,a3,a4)+a1，对于方程(19)，n>N(1234)、n>N(1342)、n>N(2341)，方程(19)有解，当n=N(1234)、n=N(1342)、n=N(2341)，方程(22)无解.

按定理2的方法，有以下定理3.

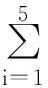
s(a1,a2,a3,a4,a5)=min{N(12345),N(12435),N(13425),N(23415),N(12534),

N(13524),N(23514),N(14523),N(24513),N(34512)},

(23)

其中N(12345)=s(123)+a4+a5，N(12435)=s(124)+a3+a5，N(13425)=s(134)+a2+a5，N(23415)=s(234)+a1+a5，N(12534)=s(125)+a3+a4，N(13524)=s(125)+a2+a4，N(23514)=s(235)+a1+a4，N(14523)=s(145)+a2+a3， N(24513)=s(245)+a1+a3，N(34512)=s(345)+a1+a2.

例1求线性型Sylvester数：①91x1+2 717x2+3 059x3；②12x1+13x2+15x3+28x4.

解①(91,2 717,3 059)=1，(91,2 717)=13=δ3，(91,3 059)=7=δ2，(2 717,3 059)=19=δ1，91=t1·13·7，t1=1，2 717=t2·13·19，t2=11， 3 059=t3·7·19，t3=23，t3>max{t1,t2}，由(14)得

s(91,2 717,3 059)=91×2 717/13+3 056×13=58 747.

② (12,13,15,28)=1.

(12,13,15)=1，(12,13)=1=δ3，(12,15)=3=δ2，(13,15)=1=δ1，由(14)得t1=4，t2=13，t3=5，t2>max{t1,t3}，由(15)式得

s(12,13,15)=12×15/3+13×3=99.

(12,13,28)=1，(12,13)=1=δ3，(12,28)=4=δ2，(13,28)=1=δ1，由(13)得t1=3，t2=13，t3=4，t2>max{t1,t3}，由(15)式得

s(12,13,15)=12×28/4+13×4=136.

(12,15,28)=1，(12,15)=3=δ3，(12,28)=4=δ2，(15,28)=1=δ1，由(13)得t1=1，t2=5，t3=7，t3>max{t1,t2}，由(14)式得

s(12,15,28)=12×15/3+28×3=144.

(13,15,28)=1，(13,15)=1=δ3，(13,28)=1=δ2，(15,28)=1=δ1，由(13)得t1=13，t2=15，t3=28，t3>max{t1,t2}，由(14)式得

s(13,15,28)=13×15+28=223.

N(1234)=s(12,13,15)+28=127，N(1243)=s(12,13,28)+15=151，

N(1342)=s(12,15,28)+13=157，N(2341)=s(13,15,28)+12=239.

所以s(12,13,15,28)=min{N(1234),N(1243),N(1342),N(2341)}=127.

参考文献

[1]柯召,孙琦.数论讲义：上册[M].北京：高等教育出版社，1986.

A Note on Sylvester Problem of Linear Form

ZHOU Hu， QIANG Hua， GU Yin-lu， SONG Zhen-zhen

(DepartmentofMathematics,YinchuanInstituteofEnergy,Yinchuan750105,China)

Abstract:An elementary method of the existence of Sylvester number of linear form aixiis proved and the calculation formulas of s(a1,a2,a3) is given. Under some added condition, the calculation formulas of s(a1,a2,a3,a4) and s(a1,a2,a3,a4,a5) are presented.

Key words:linear form； positive integer solution； Sylvester number； generalized Sylvester number

中图分类号：O156.1

文献标识码：A

文章编号：1007-0834(2015)02-0019-04

doi：10.3969/j.issn.1007-0834.2015.02.006

作者简介：周虎(1986—)，男，宁夏银川人，银川能源学院数学教研室教师.

收稿日期：2015-01-23