某型雷达对称振子阵列天线的设计与仿真

郝延刚，陆 敏

（1.海军驻南京地区雷达系统军事代表室 江苏 南京 210003;2.海军指挥学院浦口分院 江苏 南京 211800）

某型雷达对称振子阵列天线的设计与仿真

郝延刚1，陆 敏2

（1.海军驻南京地区雷达系统军事代表室 江苏 南京 210003;2.海军指挥学院浦口分院 江苏 南京 211800）

文中基于某型号雷达天线参数的设计指标，采用阵列天线的经典理论和泰勒综合法设计出符合要求的1X28阵列天线。并且还对阵列天线的阵元选择和设计，添加反射板和阵元间互耦等问题进行了研究。通过电磁场仿真软件HFSS进行了仿真试验，得出文中所设计的L波段对称振子阵列天线符合设计要求的结论。

雷达；半波振子；阵列天线；HFSS；反射板；互耦

雷达通过天线分系统获取目标的信息，天线是用于辐射或接收电磁波的传感器，是雷达的特殊组成部分[1]。本文采用使用同轴巴伦平衡变换器馈电的对称振子天线作为辐射元，泰勒分布作为阵列天线的口径分布，并且利用HFSS仿真软件设计优化出某型号雷达阵列天线。

1 阵列天线的设计

阵列天线的设计分为2个部分，首先根据设计指标综合出阵列的阵元个数、阵元间距以及激励分布，然后选择合适的阵元类型并且设计阵元，设计指标如表1所示。

表1 设计指标Tab.1 Design index

1.1 阵列孔径分布综合

工程上常用的阵列天线孔径分布的综合方法是切比雪夫综合法和泰勒综合法。本文选择泰勒分布作为阵列天线的激励分布。首先根据设计指标中的阵列天线副瓣电平（SLL）为-25 dB，由阵列天线的半功率波瓣宽度的计算公式(1)

求得N=28，d=λ/2。

然后根据公式(2)[2]，可以求得28个阵元的归一化电流。

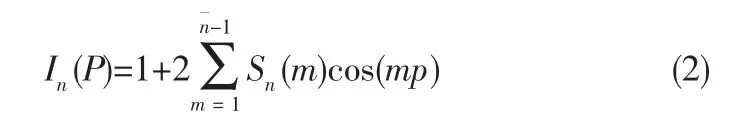
根据顺序排列的激励幅度，可以写出阵因子的表示式

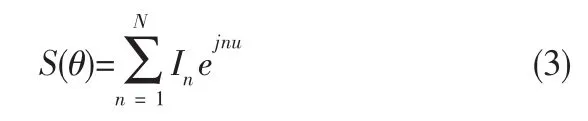
式中μ=kd cosθ+α

由公式（3）可得到泰勒阵列归一化方向图，图1为中心频率下的阵列天线方向图。从所得数据可以看出，副瓣电平和波瓣宽度符合设计要求。

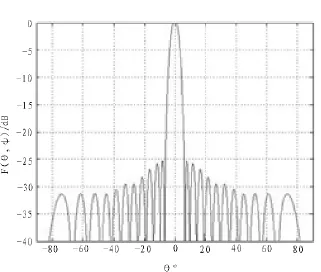
图1 方向图（中心频率）Fig.1 Radiation pattern（center frequency）

1.2 阵元的选择

阵元作为阵列天线的主要构成部件，它的主要功能是电磁波的发射和接收。通过上一节的介绍可知，阵元的种类繁多。但不是每一种形式的天线都适合作为阵元，只有根据所设计阵列天线的性能要求选择的阵元类型才是最佳的。最基本的选择标准有如下5点[3]：

1)所选择天线的方向图应该在阵列天线的扫描范围内提供合适的孔径匹配。

2)阵元的极化方式和功率要满足设计要求。

3)选择阵元时要结合所设计馈电络的类型。例如，馈电网络由微带线组成，则阵元选择微带振子为最佳。如果馈电网络是由波导组成，那么开口波导或在喇叭天线则是最佳的阵元选择。

4)阵元的机构必须牢固，能经受得起热、冲击和震动等环境。

5)最后阵元的性价比要好，不仅要满足以上的性能还要价格合理，减少设计成本。

根据以上的选择方式，并且结合本次设计的阵列天线的特殊性，本文选择对称振子天线作为阵列天线的阵元。对称振子天线是目前为止最经典、使用最广泛的天线之一，尤其是半波对称振子天线。对称振子天线不仅可以单独使用，而且还可以作为阵列天线的辐射元，实现单独对称振子所不能实现的功能，并且提高了方向性和增益。

1.3 阵元的设计

对称振子天线设计的主要任务就是传输线材料的选择和实现平衡馈电。常用的作为阵元馈电传输线的材料有矩形波导、同轴线、带状线以及微带线等。根据阵元的形式选择不同的传输线。如果辐射元为微带天线，那么最合适的馈线材料是微带线。而对称振子天线馈电部分常用同轴线作为馈线。综上所述，本文所设计的阵元馈电方式就是利用同轴线实现平衡馈电。

为了实现对对称振子的平衡馈电，必须在对称振子和同轴线之间添加不平衡到平衡的转换器，即平衡器。常用的平衡器种类很多，如Bazook平衡器、折叠式平衡器、半波长平衡器、混合电桥环平衡器、裂缝管式平衡器以及渐变形平衡器等。平衡器的选择可以根据振子的形式、结构来决定。本文所设计对称振子采用同轴巴伦平衡变换器。

馈电网络常用50 Ω的同轴线作为其传输线，而阵列天线的辐射器则是约为73 Ω的对称振子天线，这就使传输线和天线间产生了不匹配问题。本文所设计的同轴巴伦平衡变换器不仅有不平衡到平衡变换作用，同时也有阻抗变换作用。结构如图2所示。对称振子左臂与同轴线外部导体相连接，即图中的A点。对称振子右臂与同轴线内部导体和1/4波长直导线相连接，即图中B点。1/4波长直导线下端用金属环与同轴线的外壁相连接。从图2中可以看出，从A点到达B点得距离为两个1/4波长，即半波长。因此，电信号从B点传到A点得路程长正好为1/2波长，相位正好相差180°。通过此过程就可以把同轴线的不平衡转换成平衡。

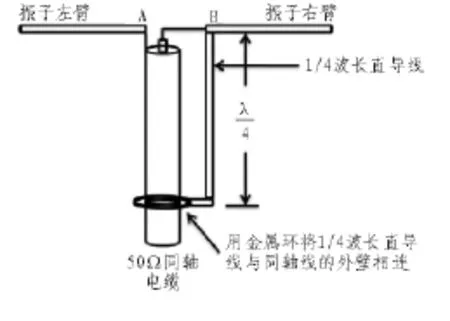
图2 同轴巴伦平衡变换器Fig.2 Coxial balance convertor

2 阵列天线系统的仿真

Ansoft公司出品的HFSS仿真软件广泛地应用于航空、航天、电子、半导体、计算机、通信等多个领域。它具备仿真精度高，可靠性强，仿真速度快，稳定成熟的特点，其自适应网格画分技术使HFSS成为高频结构设计的首选工具和行业标准。利用HFSS工具可以高效地设计各种高频结构，包括射频和微波部件、天线和天线阵，从而降低设计成本，减少设计周期，增强竞争力[4]。

2.1 对称振子天线和阵列天线的仿真

如图3所示为本文所设计的阵列天线的辐射元的整体仿真模型。模型的设计按照图2所示的采用同轴巴伦平衡变换器的对称振子，并且在对称振子的背面添加反射板。

对称振子两臂间的距离也可以对天线的性能产生影响。本文利用HFSS仿真软件的优化功能，对对称振子天线两臂的间距d进行参数扫描，得出不同间距值d的S11值。从仿真优化结果求得最佳间距为0.24 mm[5]。

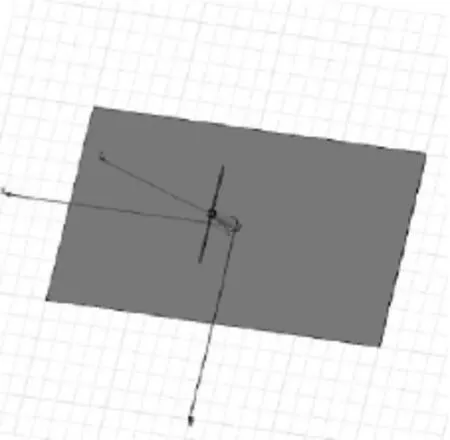
图3 对称振子天线HFSS仿真模型图Fig.3 The simulation model of doublet antenna

如图4和图5所示为称优化后对振子天线方向图和驻波比。

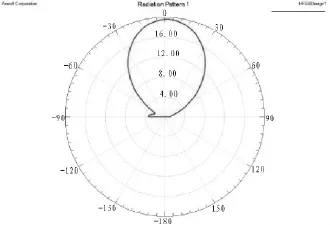
图4 对称振子天线仿真方向图Fig.4 The simulation radiation pattern of doublet antenna

图5 对称振子天线仿真驻波比Fig.5 The simulation VSWR of doublet antenna

最后将所有对称振子按照前文的设计结果排列成泰勒线阵，得到阵列天线的E面方向图仿真结果，如图6所示。

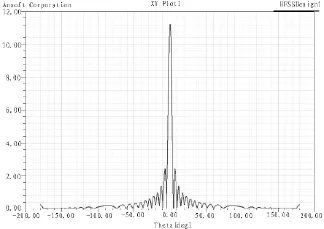
图6 阵列天线仿真方向图（中心频率）Fig.6 The simulation radiation pattern of array antenna（center frequency）

2.2 添加反射板与阵元间互耦问题的研究

为了使阵列天线的放射方向图仅在正向（Z>0）有辐射，可以在阵列天线的后面采用安装反射板的方式实现该要求，反射板可以是金属的材料制作而成的。添加反射板之后，根据镜像原理，计算阵列天线的方向图时也要把阵列单元的镜像考虑进去。

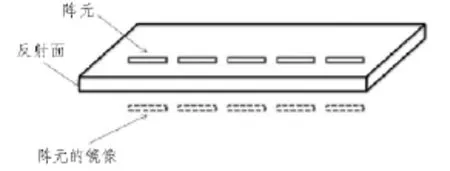
图7 反射板Fig.7 Baffle-board

如图7所示，天线阵阵元与其镜像阵元构成一个二元线阵，间距为dz，根据阵列天线阵因子计算公式，可以得到二元线阵的阵因子为：

所以，阵列天线的阵元方向图函数变成二元阵方向图函数，而天线阵的方向图函数即为：

式中，f0为半波振子方向图函数，f为天线阵的阵因子。

当两个辐射单元之间产生互耦影响时，单元的阻抗和方向图就会产生变化，从而影响整个阵列天线的性能[6]。之所以会产生互耦效应，是因为辐射单元之间靠的很近。本文所设计的阵列天线单元间距小于一个波长，所以应该考虑互耦对天线性能的影响。两个天线间的互耦度C定义为消耗在接收天线匹配负载上的功率Pr与发射天线输入功率Pt之比，即

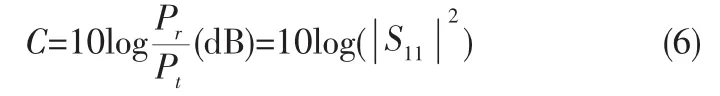
式中S21表示接收天线到发射天线间的传输系数。因此，可以通过测量相邻两个个天线间的传输参数来研究天线阵的互耦问题。表2所示，即为通过仿真软件测得各个相邻阵元间的传输系数。

从仿真数据中可以看出，最小的传输系数为-37.02 dB，所以所设计天线阵满足要求。

表2 相邻阵元间传输系数（单位：dB）Tab.2 Transm ission coefficient

3 结束语

本文设计的某型号雷达阵列天线采用25 dB泰勒分布作为阵列天线的激励分布，并且选择对称振子作为阵列天线的阵元。使用同轴巴伦平衡变换器实现了对称振子天线的平衡馈电，利用HFSS电磁场仿真软件的优化功能对对称振子天线两臂间距进行了优化设计，选择了最佳的间隔距离。最后对在阵列天线上添加反射板和阵元间互耦两个问题进行了研究，并且利用仿真软件证明本文所设计的阵列天线的互耦效应符合设计要求。

[1]束咸荣，何炳发，高铁.相控阵雷达天线[M].北京：国防工业出版社，2007.

[2]汪茂光，吕善伟，刘瑞祥．阵列天线分析与综合[M]．成都：电子科技大学出版社，1989.

[3]Robert J.Mailloux著，南京电子技术研究所译．相控阵天线手册（第二版）[M]．北京：电子工业出版社，2007.

[4]李明洋．HFSS应用详解[M].北京：人民邮电出版社，2010.

[5]曹善勇．Ansoft HFSS磁场分析与应用实例[M]．北京：中国水利水电出版社，2010.

[6]王炎，徐善驾．发射阵列互耦校正[J]．电子与信息学报．2004: 26(6):23-26. WANG Yan，XU Shan-jia．The mutual coupling calibration of emission array[J].Journal of Electronics&Information Technology，2004:26(6):23-26.

表1 性能对照表Tab.1 The comparison table of performance

4 结论

本文用VHDL语言在Xilinx Spartan6上实现了对PDCP的EEA/EIA加速处理，在ISE13.4下综合，在Modelsim 10.1c下进行仿真，得到了正确结果，各项指标均符合系统要求。系统对软件能要求较高部分的代码采用硬件实现方式，是未来软硬件一体化设计的发展趋势，特别是在高速通信设备领域。参考文献：

[1]CCSA.3GPP Specification of the 3GPP Confidentiality and Integrity Algorithms 128-EEA3&128-EIA3.Document 2: ZUC Specification[S].Beijing.China Communications Standards Association，2011.

[2]王映民，孙韶辉,等.TD-LTE技术原理与系统设计[M].北京：人民邮电出版社,2010.

[3]戈勇,李华,宁永成.基于FPGA的DES加密算法实现[J]电子科技,2013,26(7):172-176. GE Yong,LI Hua,NING Yong-cheng.Electronic science and technology[J].Electronic Science and Technology,2013,26(7): 172-176.

[4]杜红红，张文英.祖冲之算法的安全分析[J].计算机技术与发展,2012,22(6):151-155. DU Hong-hong,ZHANG Wen-ying.Security analysis on ZUC stream cipher [J].Computer Technology and Development, 2012,22(6):151-155.

[5]Clive“Max”Maxfield.FPGA World Class Designs[M].北京：人民邮电出版社,2012.

[6]Specification of the 3GPP Confidentiality and Integrity Algorithms 128-EEA3&128-EIA3.Document 3:Implementors test data[S].Beijing.China Communications Standards Association，2011.

Design and sim ulation of a model radar doublet antenna array

HAO Yan-gang1,LU Min2
（1.Military Representative office of Radar System of the Chinese PLA Navy in Nanjing,Nanjing 210003，China；2.The Pukou Institute of Naval Command College,Nanjing 211800，China）

In this paper,the design index of a certain radar antenna parameter is the basis.It uses both classical theory of the array antenna and Taylor synthesis to design 1X28 array antenna that meets the requirements.In addition,the design and selection of array element of array antenna and issue of adding reflective plate as well as the mutual coupling of array element are discussed.Finally,through the simulation and verification of HFSS,an electromagnetic field simulation software,it is proved that the designed L-band symmetrical oscillator array antenna meets the design requirements.

radar;doublet antenna;array antenna;HFSS;baffle-board;cross coupling

TN820.1

A

1674－6236（2015）07-0098-04

2014-08-06 稿件编号：201408026

郝延刚(1987—)，男，黑龙江齐齐哈尔人，硕士研究生。研究方向：雷达总体技术。