基于MATLAB的Sigma-Delta ADC中数字滤波器设计

董 阳，彭晓宏，吴艳伟

（北京工业大学 北京 100124）

基于MATLAB的Sigma-Delta ADC中数字滤波器设计

董 阳，彭晓宏，吴艳伟

（北京工业大学 北京 100124）

为了将Sigma-Delta ADC中的SDM（Sigma-Delta Modulator）的输出码流降采样以达到Nyquist采样频率，基于实际的AUDIO CODEC项目，本文对两种数字滤波器（FIR（Finite Impulse Response）和IIR（Infinite Impulse Response））的MATLAB设计进行了描述和比较。其所需处理的SDM输出码流的过采样频率为11.2896MHz，数字滤波器完成256倍的降采样最终达到采样频率为44.1MHz，在音频范围内其最终仿真结果均达到SNDR在14bits以上。

Sigma-Delta ADC；降采样；FIR；IIR

Sigma-Delta ADC在高精度ADC设计中广泛得到应用，其基本原理是通过SDM的过采样将量化噪声推向高频，并通过数字滤波器完成滤波和降采样，最终得到精度较高的信号。数字滤波器是Sigma-Delta ADC中至关重要的组成部分，几乎占据整个IP的绝大部分，所以对数字滤波器的研究显得尤为重要。

两种数字滤波器（IIR和FIR）各有其优缺点，在Sigma-Delta ADC的设计中，由于非递归FIR滤波器系统的绝对稳定性和线性相位，其在实际电路设计中广泛得到使用。但是其缺点是硬件消耗过大，为了解决这个问题，许多学者通过算法分析提出来一些切实可行的方案。

例如：一种方法是Kaiser和 Hamming[1]提出来的，利用相互连接等同子滤波器并通过合理的加法乘法运算得到的FIR滤波器结构就能节省硬件消耗并且在文献[2]中得到扩展沿用；另一种方法是利用级联互联等同子滤波器实现FIR滤波器结构，文献[3]中有详细分析。相比FIR滤波器，在等同的频率响应系统中IIR滤波器通常会带来相对较小的硬件消耗，以至于占用较小的芯片面积，这在特定的应用中是可以考虑的。可见，根据实际应用需求，对于两种数字滤波器的折中选择是尤为重要的。

1 FIR滤波器和IIR滤波器概述

关于FIR滤波器，应用频率转换特性，将整个复合滤波器分解成几个相同子模块。其传递函数H（z）表示为：

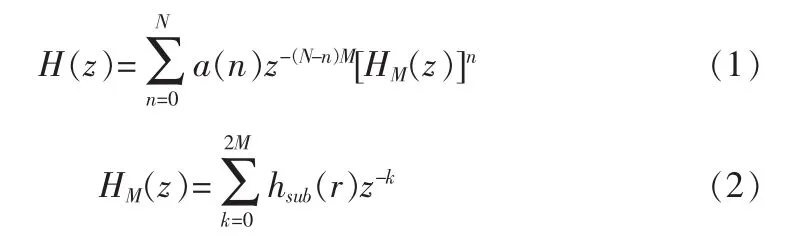
其中，线性相位FIR滤波器的阶数为2M+1。子滤波器HM（z）由频率转换特性决定的，系数a（n）是有原型滤波器决定的。如文献[4]描述，通过控制a（n）和子滤波器的系数可以改变这个结构的频率响应特性。

然而，由于IIR滤波器具有较少的计算要求和较少的硬件消耗的优势，在对相位要求没那么严格的应用当中，例如：Sigma-Delta ADC[5]音频信号处理。采用IIR滤波结构完成SDM输出码字的降采样功能非常具有实际价值。其IIR滤波器的传递函数H（z）的表示为：

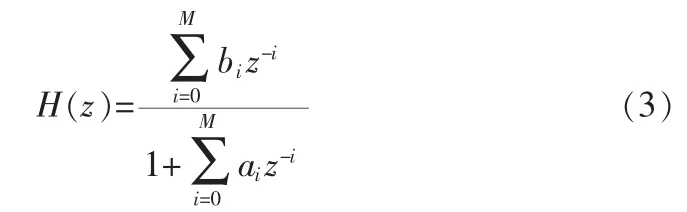
其中，ai和bi是IIR滤波器的系数。通过合理的设计ai和bi的值实现所要求IIR滤波器。

由于传统的数字滤波器设计是非常复杂的，尤其是涉及到高阶滤波器结构。故为了高效可行的完成对数字滤波器的设计，本文利用FDATOOL完成对IIR滤波器架构的设计，而FIR数字滤波器的设计是通过Simulink模型搭建和Toolbox工具箱来完成的。

2 IIR滤波器结构

基于FIR滤波器本身所具备的稳定性优势，其完成256倍降采样的整体框架是由CIC，HBF1，HBF2三级级联组成，其中CIC完成64降采样，两级HBF分别完成2倍降采样，以最终达到Nyquist采样频率。系统频率响应的每一级输出的数字码流的采样频率分别为：176.4 kHz，88.2 kHz，44.1 kHz。如果采用一级直接完成256倍降采样，对滤波器要求极高而引起极大的硬件消耗。

CIC模型结构[6]如图1所示，z-1为单位延迟单元，convert模块（本文其他数字滤波器结构均有此模块，但未在图中标出）用于限定字长。由于CIC的阶数至少比SDM的多1，所以这里CIC为3阶。其传递函数表达式为：

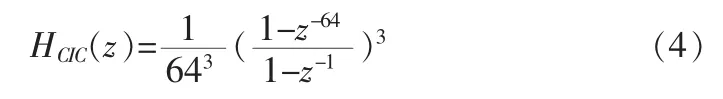
HBF1和HBF2采用的是Saramaki提出的结构模型，分别如图2和图4所示，其中F2为HBF的子滤波器，图3为HBF1的内插子滤波器，图5为HBF2的内插子滤波器。相应的系数（理想仿真值和CSD（Canonical Signed-Digit）值）如表1和表2所示，这些系数是通过Toolbox工具箱中的designHBF函数得到的。图中的In1和In2是相同的输入信号，只是相位相差π。

图1 CIC模型结构Fig.1 Structure diagram of CIC

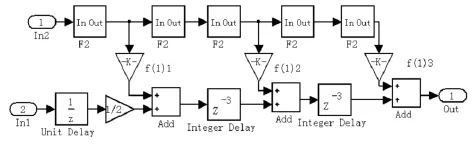
图2 HBF1的结构模型Fig.2 Structure diagram of HBF1

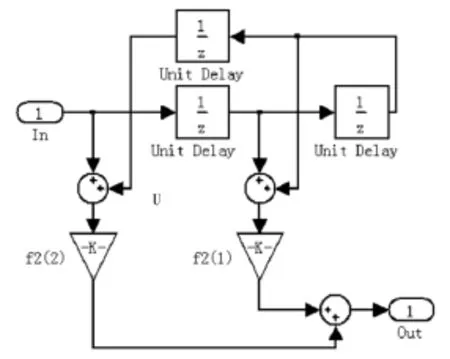
图3 HBF 1的子滤波器Fig.3 Subfilter of HBF1

3 IIR滤波器结构

IIR滤波器属于递归系统，其结构简单易于实现，占用的芯片面积小，但是相位随频率非线性变化，使得信号在时域会发生失真，这对于相位要求不是特别严格的场合有很重要的意义。由于FIR滤波器自身的缺陷，本文同样设计了IIR滤波器，其整体结构相对于FIR滤波器的区别是:把两级HBF用一个二阶IIR滤波器代替，如图6所示。这里的IIR滤波器是根据切比雪夫原理通过FDAtool来实现的，FDATool设计数字滤波器的工具箱包含了信号处理中所有的滤波器设计方法，这里，只需设定既定的参数即可得到所需要的IIR数字滤波器。由于IIR滤波器本身的相位非线性，所以其不能设计成为高阶系统（阶数越高线性度越差），本设计完成的是2阶系统。关于系统稳定性，因为CIC为FIR滤波器（稳定），传递函数为X（z），chebyshev法实现的IIR滤波器（稳定），传递函数为Y（z），当把两个传递函数相乘时，X（z）*Y（z），仍为IIR滤波器，其分母为Y（z）的分母，令其为零得到同Y（z）一样的极点分布，故IIR数字滤波器部分依旧稳定。最终模型同FIR滤波器一样，IIR滤波器的系数同样也要CSD化。

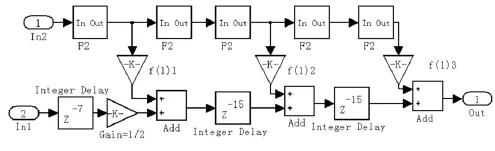
图4 HBF2的结构模型Fig.4 Structure diagram of HBF2

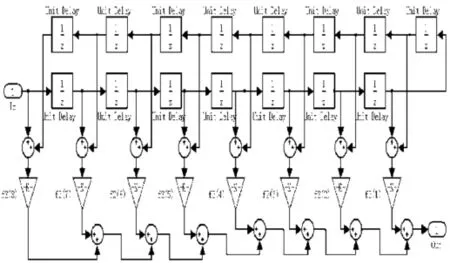
图5 HBF2的子滤波器Fig.5 Subfilter of HBF2

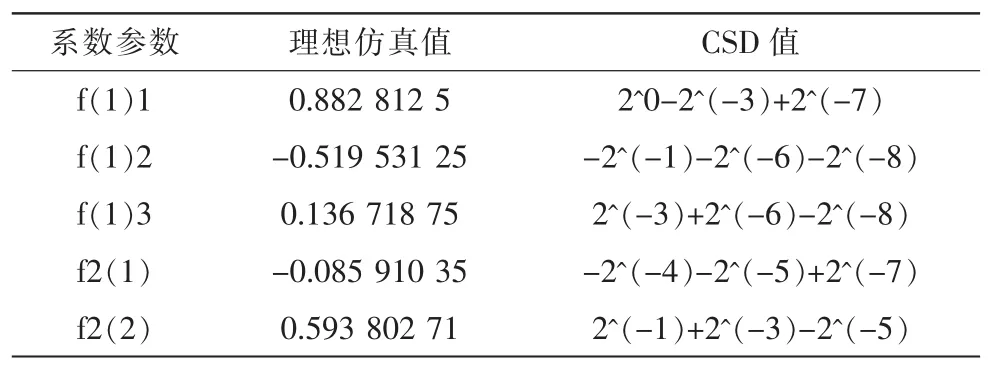
表1 HBF1的系数Tab.1 Coefficients of HBF1

表2 HBF2的系数Tab.2 Coefficients of HBF2

图6 IIR整体结构框图Fig.6 Overall framework of IIR

4 仿真结果

数字滤波器主要是用来完成带外噪声的滤除和降采样功能，首先看FIR滤波器，CIC结构模型为3阶，完成64倍的降采样同时粗略滤除了带外噪声。两级HBF进一步完成滤波并降采样到Nyquist采样频率，其中HBF1为151阶，通带纹波0.015 dB，阻带衰减为-61.9 dB；HBF2为31阶，通带纹波0.000 8 dB，阻带衰减-81.1 dB，这个结果可以通过频域冲击响应分析得到。FIR滤波器系统最终输出码流的SNDR为92.8 dB，ENOB为15.12 bits，如图7所示。本设计中，FIR滤波器和IIR滤波器主要的区别在于CIC模型后面的部分，IIR滤波器是切比雪夫模型结构而FIR滤波器为两级HBF滤波器。低阶IIR滤波器切比雪夫模型的设计对相位的要求并没有那么严格，故在时域内并不会出现过于明显的失真，出于较低硬件消耗的考虑，这种结构在音频信号处理中依旧是可以得到应用的，其仿真结果如 8所示，SNDR为 86.8 dB，ENOB为14.13 bits，两种结构均达到预先要求的14 bits精度。

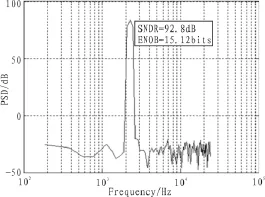
图7 FIR仿真结果Fig.7 Simulation result of FIR

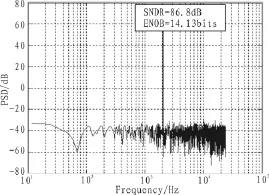
图8 IIR仿真结果Fig.8 Simulation result of IIR

5 结 论

本文介绍的是AUDIO CODEC项目中Sigma-Delta ADC数字滤波器的设计，其中FIR滤波器的结构模型和系数CSD化为项目的实际要求所定，其结构用Verilog硬件描述语言数字实现，完成了与MATLAB模型的精确数据比对，并且成功流片。IIR滤波器的设计是为了节省硬件消耗所作出的探索，其MATLAB实现符合本项目所要求的14 bits精度。两种数字滤波器之间的折中选择是本文所要重点阐述的内容，如果芯片面积宽裕，采用线性相位的FIR滤波器来完成数字滤波和降采样是首选方案，因为从仿真图上可以看出，FIR滤波器相对IIR滤波器的最终仿真结果有效位数要多出近1bit。但是实际要求若对面积要求苛刻，在对相位要求没那么高的系统当中，例如本设计要求的14 bits Sigma-Delta ADC设计，IIR数字滤波器是非常具有实际价值的。

[1]Kaiser J F，Hamming R W.Sharpening the response of asymmetric nonrecursive filter by multiple use of the same filter[J].IEEE Trans.Acoust.，Speech，Signal Processing，1997:415-422.

[2]Hartnett R J，Boudreaux-Bartels G F.Improved filtersharpening[J].IEEE Trans.Signal Processing，1995，43（12）: 2805-2810.

[3]Oppenheim A V，Mecklenbrluker W F，Mersereau R M.Variable cutoff linear phase digital filters[J].IEEE Trans.CircuitsSyst.，1976:199-203.

[4]Saramaki T.Design of FIR filters as a tapped cascadedinterconnection of identical subfilters[J].IEEE Trans.Circuits Syst.，1987:1011-1029.

[5]Daneshgaran F，Laddomada M.A novel class of decimation filtersforΣ△A/D converters[J].W ireless Communications and MobileComputing，2002:867-882.

[6]HOGENAUER E B.An economical class of digital filters fordecimation and interpolation[J].IEEE Trans.Acoust.Speech SignalProcess.，1981:155-162.

Design of digitalfilter for Sigma-Delta ADC based on MATLAB

DONG Yang，PENG Xiao-hong，WU Yan-wei
（Beijing University of Technology，Beijing 100124，China）

In order to down-sample the output codes of SDM（Sigma-Delta Modulator）to Nyquist frequency within Sigma-Delta ADC.In this paper，two types of digital filters have been shown and the comparison of the FIR（Finite Impulse Response）and IIR （InfiniteImpulse Response）digital filter are presented based on MATLAB in the actual program AUDIO CODEC，the input signal need to be coped is 11.2896 MHz digital codes and 256 times down-sampling will be realized by digital filters to achieve 44.1MHz at the final output，both of the simulation results achieved SNDR above 14bits in audio frequency range.

Sigma-Delta ADC；down-sample；FIR；IIR

TN302；TN432

A

1674－6236（2015）10-0175-04

2014-08-30 稿件编号：201408114

国家自然科学基金(61204040,60976028)；北京市自然科学基金(4123092)；教育部博士点基金(20121103120018)

董 阳（1989—），男，河北廊坊人，硕士研究生。研究方向：模拟集成电路设计。