基于小波变换和粗糙集的电力电子电路故障诊断方法

王智弘，李东辉

(大连交通大学电气信息学院，辽宁大连116028)

0 引言

电力电子电路作为整流器，逆变器的核心部件，其应用越来越广泛，因此研究电力电子电路的故障诊断技术具有非常重要的意义。为了实现故障的快速识别，诊断与定位，国内外的学者们提出了许多电力电子电路的故障诊断方法。例如:文献［1-2］研究了主要采用支持向量机的电力电子电路故障诊断技术，文献［3］研究了混沌系统模型和事件辨识的电力电子电路故障诊断技术，文献［4-5］应用了小波变换和神经网络的方法来诊断电力电子电路，文献［6］研究了采用量子计算和神经网络相结合的量子神经网络的诊断技术，克服了传统神经网络的不足，文献［7］采用了分形的方法进行了故障诊断。

粗糙集理论是一种刻划不完整性和不确定性的数学工具，可以应用到电力电子电路的故障诊断中去，如文献［8］利用约简决策表实现了故障的诊断，但因为应用傅里叶变换得到故障的特征，导致其决策表的建立过程相对比较繁琐，推广有一定困难。

本文利用小波变换较强的信号局部处理能力，提取故障特征能量值，建立决策表，应用粗糙集进行故障诊断。最后通过建模仿真，验证了建立决策表的快速和方法的有效性。

1 粗糙集理论基础

定义1［9］51:令决策表系统为 M≤U，R，V，f＞ ，R=P∪D 是属性集合，子集P={ai/i=1……，m}和D={d}分别称为条件属性集和决策属性集，U={x1，x2，…，xn}是论域，ai(xj)是样本 xj在属性ai上的取值。CD(i，j)表示可辨识矩阵中的第i行j列的元素，则可辨识矩阵CD定义为:

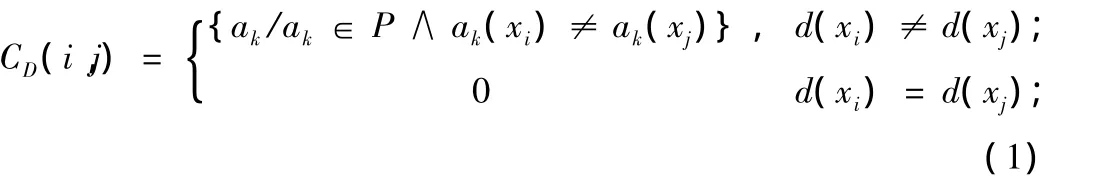
定义2［9］119:设U为一个论域，P和Q为定义在U上的两个等价关系簇，Q的P正域记为POSP(Q)，定义为:POSP(Q)=X∪U/QP-(X)。若POSP(Q)=POS(P{r})(Q)，则称r为P中相对于

∈Q可省略的(不必要的)，简称P中Q可省略的;否则，称r为P中相对于Q不可省略的(必要的)。

其中 i，j=1，…，n。

2 基于粗糙集的电力电子电路故障诊断

2.1 诊断模型的建立

基于粗糙集的电力电子电路故障诊断步骤如下:

①通过MATLAB仿真，导出各故障下输出电压U的波形图;②应用小波变换，对波形图进行6层小波分解，提取出6个低频能量值和一个高频能量值，建立论域U，对电力电子电路进行分类，确定条件属性C和决策属性D;③依据定义1和定义2计算条件属性的约简;④对约简后的决策表进行值约简;⑤提取规则，形成诊断知识库。

其流程图如图1所示。

三相桥式整流电路如图2所示。

2.2 具体步骤

2.2.1 条件属性集合决策属性集

由故障仿真，得出触发角在某种特定故障下的0°～90°的波形图，通过6层小波分解每个波形图得到一个高频能量ca1和6个低频能量 cd1，cd2，cd3，cd4，cd5，cd6作为条件属性集。

由电力电子电路每一个故障作为一个决策属性，构建决策属性集。由表 1 所示:表中 1.2.3.4.5，6，7 分别为 d1，d2，d3，d4，d5，d6，d7

2.2.2 建立决策表

经过小波分解得到24组数据，作为决策表的条件属性，建立决策表。

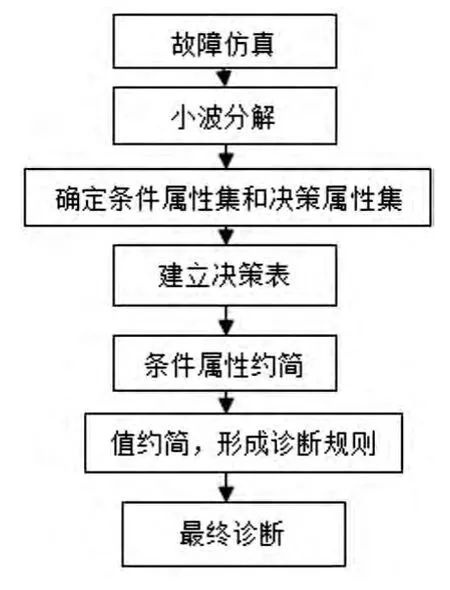
图1 故障诊断模型流程图

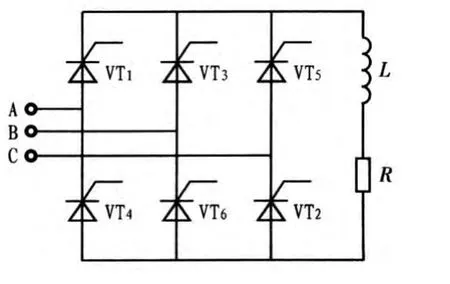
图2 三相桥式整流电路

表1 决策集合

2.2.3 数据离散化

运用粗糙集理论处理决策表时，要求决策表中的值用离散数据表达，首先对决策表进行离散化。

为了数据处理的方便，在数据离散化前，先对其进行归一化，取样本集中最大的数 pmax，样本集中最小的数 pmin，则 y=(xpmin)/(pmax-pmin)。

对归一化后的数据，本文采用等距离划分算法［9］102。在本样本中，经验证，k=5时，样本分类代表性最好。例如，某个属性，最大属性值为xmax，最小属性值为xmin，所以，断点间隔为δ=(xmax-xmin)/k。

经过归一化，离散化后删去相同决策行的决策表如表2所示。

2.2.4 条件属性的约简

依据定义1，定义2对条件属性进行约简，应用可辨识矩阵法，可得到决策表的约简{ca1，cd1，cd2，cd3，cd4}，经过约简后的决策表，保持了原决策表的分类能力，但所需要的条件确实大为减少了。

2.2.5 约简抽取规则集

对于决策表中的任意条件属性，如果去掉该条件属性，该规则不和规则集中其他规则冲突，那么就可以从该规则中去掉该条件属性，简化后可以得到最小约简，(“*”表示值约简，约去的数)如表3所示。

表2 决策表

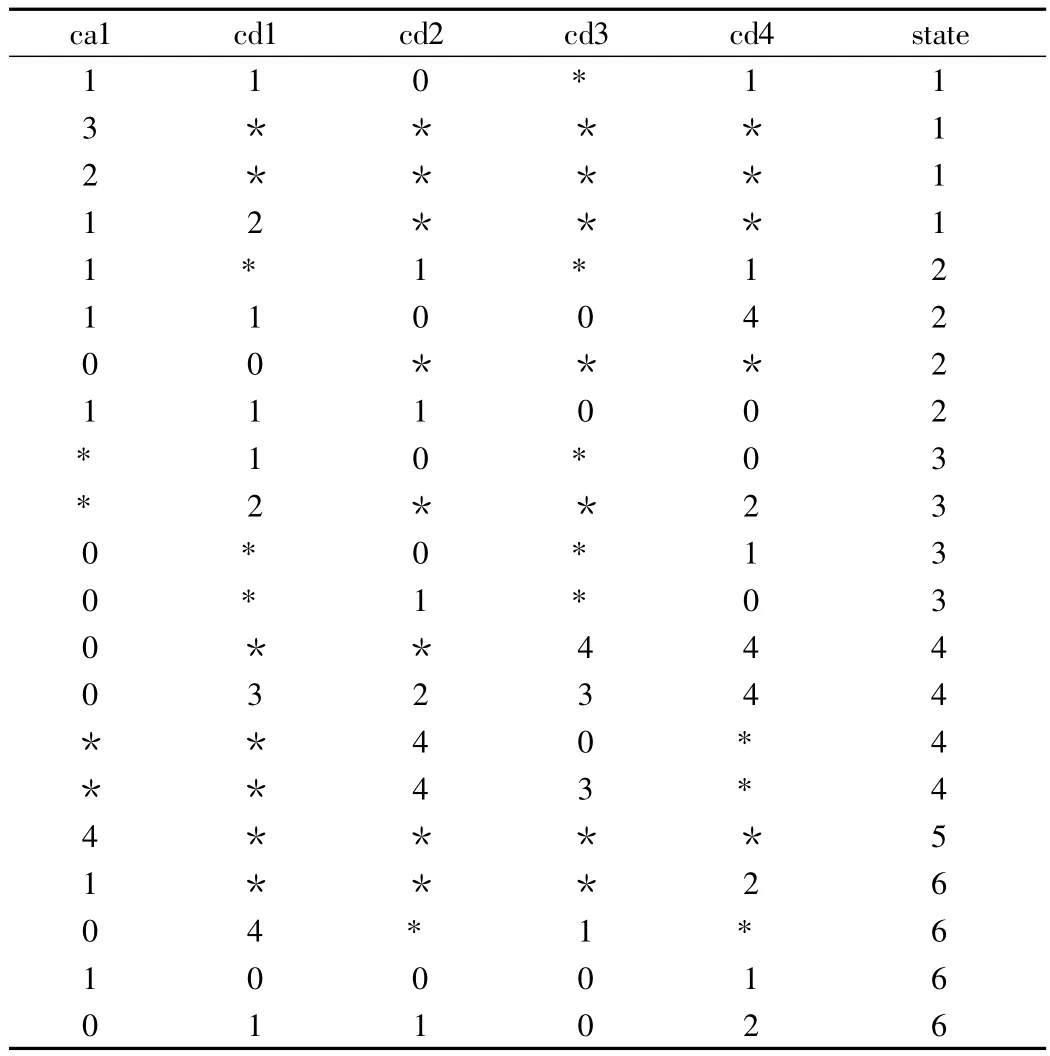
表3 最简决策表

从表3中抽取规则集:

规则 1:if［(ca1=1and cd1=1 and cd2=0 and cd4=1)or(ca1=3)or(ca1=2)or(ca1=1 and cd1=2)］then(“正常”)

规则 2:if［(ca1=1 and cd2=1 and cd4=1)or(ca1=0 and cd1=0)or(ca1=1and cd1=1 and cd2=1)or(cda1=1 and cd1=1 and cd2=0 and cd3=0 and cd4=4)］then(“交流变压器一次侧掉线”)

规则 3:if［(ca1=0 and cd2=0 and cd4=1)or(cd1=2 and cd4=2)or(cd1=1 and cd2=0 and cd4=0)or(ca1=0 and cd2=1 and cd4=0)］then(“单晶闸管断开”)

规则 4:if［(ca1=0 and cd3=4 and cd4=4)or(cd2=4 and cd3=0)or(ca1=0 and cd1=3 and cd2=2 and cd3=3 and cd4=4)or(cd2=4 and cd3=3)］then(“同相双晶闸管断开”)

规则5:if(ca1=4)then(“同组双晶闸管断开”)

规则 6:if［(ca1=0 and cd1=4 and cd3=1)or(ca1=1 and cd4=2)or(ca1=1 and cd1=0 and cd2=0 and cd3=0 and cd4=0)or(ca1=0 and cd1=1 and cd2=1 and cd3=0 and cd4=2)］then(“交叉双晶闸管断开”)

2.2.6 验证

改变仿真图负载参数，得到一组故障数据，来检测此方法的准确性经归一化，离散化后的结果，如表4所示。

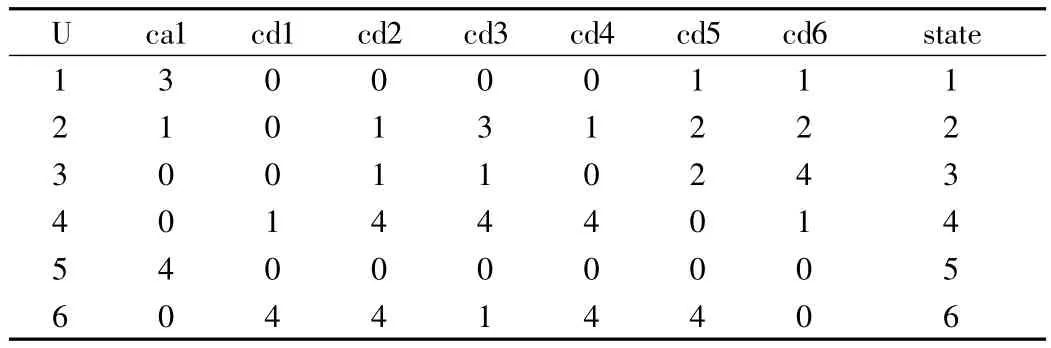
表4 离散化验证数据

用提取的规则诊断，能准确的诊断出所属故障，前面所属样本提取的规则适用于本样本，且样本越多越好，而且，所提取的规则还同样适用于以后的数据。

3 结束语

本文对于电力电子电路故障的诊断方法进行了研究，利用小波变换处理局部信号能力强的特点，发挥了粗糙集去除数据的冗余属性和获取潜在规律方面的独特优势。分析建模方法与仿真结果，本文得到以下结论:

1)利用小波变换，提取故障特征能量值，明显简化了构造决策表的过程。

2)应用粗糙集去除决策表的冗余属性，构造最简决策表，从表中获取潜在的依赖模型，得到规则，经过验证，该方法是准确而有效的。

3)粗糙集的一大优点就是可以将检测不出的数据重新提取规则，来完善原始规则集，这样规则表就会越来越完善，效率也越来越高。

4)该方法可以正确诊断电力电子电路的主要故障，但对于某个具体器件损坏的精确定位方法，尚需深入研究。

5)该方法可以推广到其他电力电子电路的故障诊断中。

［1］胡清，王荣杰，詹宜巨.基于支持向量机的电力电子电路故障诊断技术［J］.中国电机工程学报，2008，28(12):107-111.

［2］崔江，王友仁，刘权.基于高阶谱与支持向量机的电力电子电路故障诊断技术［J］.中国电机工程学报，2007，20(10):62-65.

［3］张志学，马皓，毛兴云.基于混杂系统模型和事件辨识的电力电子电路故障诊断［J］.中国电机工程学报，2005，25(3):49-53.

［4］韩晓静.基于小波变换与神经网络的电力电子电路故障诊断研究［D］.南京:南京航空航天大学，2008.

［5］徐丽丽.基于小波变换—神经网络的电力电子电路故障诊断［D］.内蒙古:内蒙古工业大学，2009.

［6］龙伯华，谭阳红，计慧，等.基于量子神经网络的电力电子电路故障诊断［J］.电工技术学报，2009，24(10):170-175.

［7］李沁，张劲松.基于分形的电力电子电路故障诊断［J］.电气技术，2007，8(11):27-30.

［8］刘庆珍，蔡金锭，涂娟.基于粗糙集理论的电力电子电路故障诊断［J］.福建工程学院学报，2004，2(4):422-425.

［9］王国胤.Rough集理论与知识获取［M］.西安:西安交通大学出版社，2001.