基于MCNP5的凸度仪固有散射影响分析

胡克敏，吴志芳，苗积臣，张玉爱，李立涛（清华大学核能与新能源技术研究院核检测技术北京市重点实验室，北京 100084）

基于MCNP5的凸度仪固有散射影响分析

胡克敏，吴志芳，苗积臣，张玉爱，李立涛
（清华大学核能与新能源技术研究院核检测技术北京市重点实验室，北京 100084）

摘要：本文采用MCNP5软件建立了凸度仪模拟计算模型，并对其进行实验结果验证。分析了凸度仪固有散射的影响，随待测钢板厚度的增大，固有散射影响减小，对1～15mm厚度的钢板，系统固有散射占总散射影响的10%以下，而对大于15mm厚度的钢板，系统固有散射可近似为零。此外，对散射因子曲线在非对应源附近的鼓包现象进行了分析，分析结果表明，探测器支架具有防止另一排探测器散射干扰的作用。

关键词：散射校正；凸度仪；MCNP5

凸度仪是热轧钢板生产线上检测和控制板材凸度的关键设备，其精度越高，所产板材质量越高，过去此系统的生产技术主要被国外几家大公司垄断。目前清华大学核能与新能源技术研究院研制的凸度在线检测系统［1］实验样机已打破这一垄断，对0．9～25mm厚度范围内的被测钢板，达到±0．1%的测量精度，其中散射影响分析及校正是保证其高精度的关键因素。从散射来源分类，主要包括被测钢板自身造成的散射和凸度仪系统部件的散射两部分。凸度仪系统部件散射，又称固有散射，与系统结构、被测钢板、射线源和环境等均相关，影响因素复杂，很难通过理论模型分析研究。

蒙特卡罗（MC）方法是以概率统计、随机抽样为理论基础，真实地描述各粒子输运问题、物理实验过程等，进而解决理论分析、数值计算等难以解决的实际问题［2］，所描述问题、系统越复杂，越能凸显MC方法的优越性，因此，基于凸度仪复杂的固有散射影响分析，必然首选MC方法。MC方法目前至少有5种计算粒子输运的程序软件［3－4］。本文采用通用性、几何能力和方差技巧等方面均较强，且具有可视化界面的MCNP5软件［5］，建立与实验样机1∶1尺寸的仿真计算模型，并对其进行实验结果验证。基于此仿真模型，定量分析凸度仪固有散射影响及其随被测钢板厚度的变化情况，并给出可降低系统固有散射影响的建议方案。

1　凸度仪仿真模型

凸度仪结构示意图如图1所示，主体支撑结构C形架由上臂、侧臂和下臂组成，材料为304不锈钢。上臂内安置两台相同的COMET MXR－225／02／FB型X光机，通过上臂下方的准直机构，将射线源准直为具有一定宽度的扇形束从上臂出射；下臂结构相对复杂，主要是两排电离室探测器，每排224路，各自对应S1、S2射线源，其排列方式在保证窗口中心正对射线源的同时，每路探测器以自身的一个角点为基准沿水平方向排列，图2为下臂剖面图（x－z面），虚线框内为扇形射线束照射区域，此区域各主要部件参数列于表1。

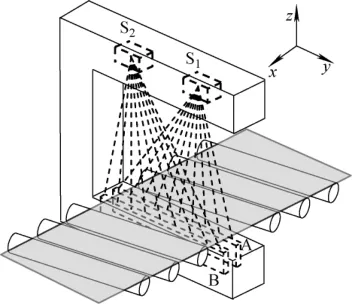
图1　 凸度仪结构示意图Fig．1 Structure diagram of profile gauge

图2　 下臂剖面图Fig．2 Sectional view diagram of lower arm

表1　 射线照射区域内各主要部件参数Table 1 Parameters of main components within irradiated area

基于上述参数建立凸度仪仿真模型，射线源S1、S2分别设置为恰好覆盖各自224路探测器面的扇形束；下臂结构稍作简化，但保留射线束照射区域的所有部件；C行架的上臂、侧臂和下臂材料均为304不锈钢；被测钢板下表面至探测面的距离为60cm；凸度仪仿真模型在MCNP5软件可视界面下的显示如图3～7所示。

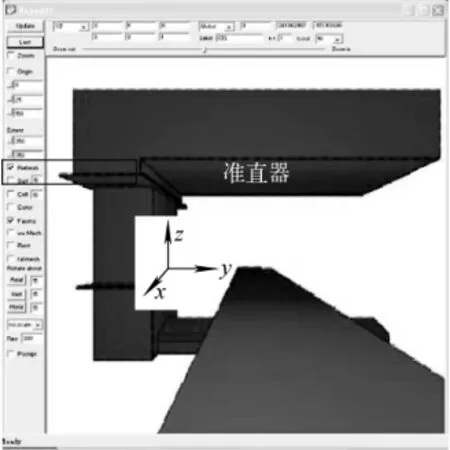
图3　 凸度仪仿真模型3D显示Fig．3 Simulation model 3Ddisplayof profile gauge

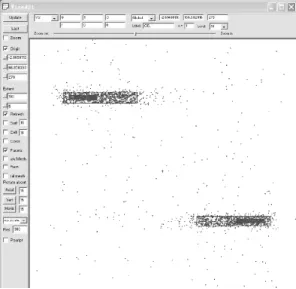
图4　 上臂粒子出射口Fig．4 Particle exit port of upper arm

2　仿真模型计算结果验证分析

基于仿真计算模型，设置被测钢板宽度为1 700mm，厚度为10mm；射线源采用管电压180kV下的X光机输出能谱（由MCNP5建模计算得到），将此模型下的散射因子计算结果与实验结果对比验证分析，分析结果如图8所示。

定义散射因子（SPR）为：

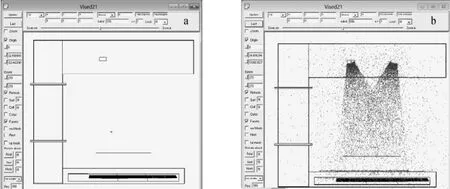
图5　 仿真模型剖面（y－z面）图（a）及粒子径迹图（b）Fig．5 Sectional view（y－z plane）diagram（a）and particle track diagram（b）of simulation model

其中，MCNP5模型计算过程中采用＊F1计数卡，与电离室计数相对应。

由图8可看出，仿真模型计算结果与实验结果基本吻合。在钢板边缘，散射因子较大，曲线较陡；在靠近正对射线源处，散射因子最小；探测器距正对射线源越远，射线斜穿钢板厚度越大，散射因子亦越大，这符合康普顿散射的基本物理规律。仿真模型计算结果与实验结果存在一定的偏差，主要原因为：1）由于实验用钢板宽度和钢板在辊轴上的位置是人工测量确定的，存在一定的误差；2）实验所得A、B排探测器散射因子曲线在远离对应源的钢板边缘位置，相比仿真模型结果出现明显鼓包现象，如图9所示。

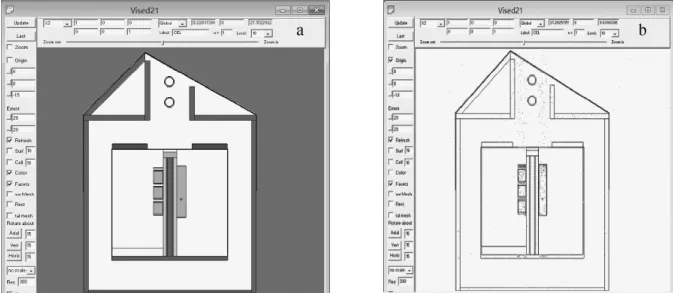
图6　 仿真模型下臂剖面（x－z面）图（a）及粒子径迹图（b）Fig．6 Sectional view（x－z plane）diagram（a）and particle track diagram（b）of lower arm in simulation model

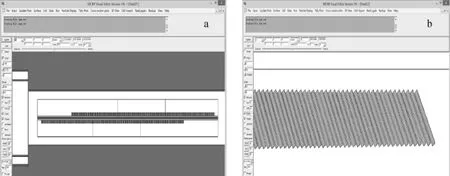
图7　 仿真模型探测器排列（x－y面）图（a）及排列细节（y－z面）图（b）Fig．7 Arrangement of detectors（x－yplane）diagram（a）andarrangement detail（y－z plane）diagram（b）

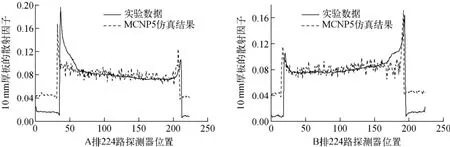
图8　 散射因子计算结果与实验结果对比Fig．8 Comparison of scatter－to－primary ratio between simulation result and experimental result

图9中，阴影区域1是A源射线经钢板散射后进入到B排探测器，此散射量远小于B排探测器接收的透射量，因此可忽略；阴影区域2是A源直接照射到A排探测器上发生散射后进入B排探测器，而此位置的B排探测器远离B源，且射线束经钢板厚度的衰减，透射量减少，增加的散射量与减少的透射量的比值（即散射因子）增大，形成鼓包现象；钢板厚度越大，接收的透射量越少，鼓包现象也将越明显。

图9　 散射因子曲线鼓包现象分析Fig．9 Analysis of SPR curve bulge phenomenon

MCNP5计算结果并未明显鼓包的原因是，仿真模型的扇形束宽度恰好照射探测器窗面积，且中间有探测器支架吸收。而实验结果中扇形束的宽度无法测到，且探测器支架结构相对复杂，仿真模型的简化造成探测器支架的吸收率增大，因此会出现鼓包现象。

3　仿真模型下凸度仪固有散射影响分析

本部分内容用到两个模型：1）模型1，凸度仪仿真模型；2）模型2，只有射线源，钢板和A、B两排探测器3部分的计算模型。

基于上述两个模型，分别计算厚度为1、5、10、15mm，宽度为1 700mm钢板的散射因子，由上述公式计算固有散射因子及其η。图10、11为B排探测器散射因子、固有散射因子及其η的曲线分布，可看出：1）随钢板厚度的增大，除曲线鼓包范围探测器，凸度仪系统固有散射影响减小，到15mm厚度时，探测器的散射来源可近似全部为钢板，固有散射影响可忽略；2）随钢板厚度的增大，模型2的散射因子曲线鼓包现象变大，说明直接照射在A排的射线散射后造成B排的散射影响变大，与仿真模型对比，探测器支架起了很大的防A排散射干扰的作用；3）1～15mm厚度被测钢板，除鼓包范围探测器外，其余各路探测器的η小于10%，即固有散射影响占总散射影响的10%以下，鼓包范围探测器中，固有散射为负值。

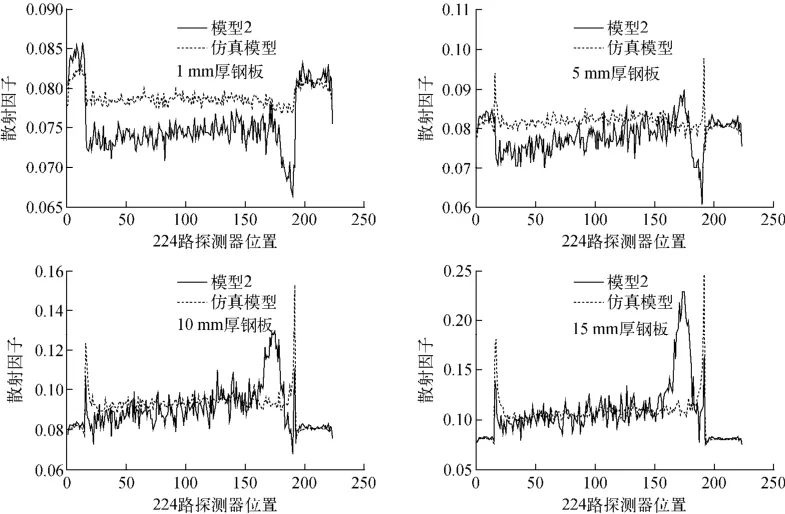
图10　 不同钢板厚度下仿真模型和模型2的SPR分布Fig．10 SPR distributions of simulation model and model 2 under different plate thicknesses

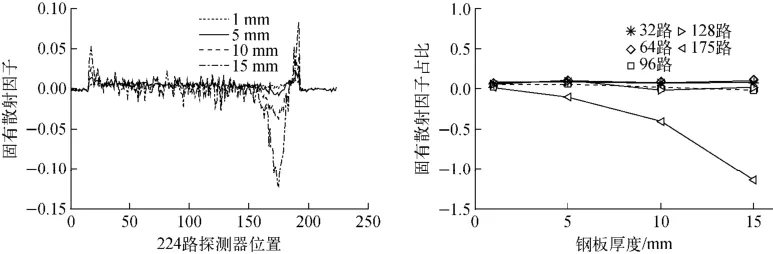
图11　 固有散射因子及η分布Fig．11 Distributions of inherent SPR andη

4　结论

为分析凸度仪固有散射影响，本文采用蒙特卡罗方法MCNP5软件，建立了凸度仪系统仿真模型，并给出了可视化界面下的3D显示和各方向的剖面图；采用实验数据对仿真模型计算结果进行验证，两者基本吻合，但实验数据存在鼓包现象，经分析为非对应源（如B源）直接照射到与它对应的探测器（B排探测器）上发生散射后对此探测器（A排探测器）的影响；最后分析了凸度仪固有散射的影响，随待测钢板厚度的增大，固有散射影响减小，对大于15mm厚度的钢板，系统固有散射可近似为零；对1～15mm厚度的钢板，系统固有散射占总散射影响的10%以下。

参考文献：

［1］ 苗积臣，吴志芳，张玉爱，等．凸度检测系统厚度测量精度分析［J］．原子能科学技术，2011，45（8）：983－986．MIAO Jichen，WU Zhifang，ZHANG Yuai，et al．Analysis of thickness measure precision in X－ray profile gauge［J］．Atomic Energy Science and Technology，2011，45（8）：983－986（in Chinese）．

［2］ 裴鹿成，张孝泽．蒙特卡罗方法及其在粒子输运问题中的应用［M］．北京：科学出版社，1980．

［3］ 徐淑艳．蒙特卡罗方法在实验核物理中的应用［M］．北京：原子能出版社，2006．

［4］ 邱睿，李君利，武祯，等．四种蒙特卡罗程序的比较计算［J］．原子能科学技术，2008，42（12）：1 149－1 152．QIU Rui，LI Junli，WU Zhen，et al．Comparison calculation of four Monte－Carlo codes［J］．Atomic Energy Science and Technology，2008，42（12）：1 149－1 152（in Chinese）．

［5］ MCNP：A general Monte Carlo N－particle transport code［M］．［S．l．］：［s．n．］，2003．

Analysis of Inherent Scattering Based on MCNP5 for Profile Gauge

HU Ke－min，WU Zhi－fang，MIAO Ji－chen，ZHANG Yu－ai，LI Li－tao
（Beijing Key Laboratory on Nuclear Detection and Measurement Technology，
Institute of Nuclear and New Energy Technology，Tsinghua University，Beijing100084，China）

Abstract：In this paper，based on MCNP5，the simulation model of profile gauge was established and verified by the experimental data．The inherent scattering of profile gauge was analyzed．The value of inherent scattering decreases with the increase of steel plate thickness．For the thickness of 1mm to 15mm，the inherent scattering accounts for less than 10%of the total scattering effect，and for over 15 mm thickness steel plate，inherent scattering can be approximated as zero．In addition，the analysis result of the bulge phenomenon for the scatter－to－primary ratio（SPR）curve proves that the detector stent can prevent another detector row’s scattering．

Key words：scattering correction；profile gauge；MCNP5

作者简介：胡克敏（1985—），女，山东滕州人，博士研究生，核科学与技术专业

基金项目：北京市科委研发攻关课题资助项目（Z080903027508）

收稿日期：2014－03－18；修回日期：2014－10－19

doi：10．7538／yzk．2015．49．08．1477

文章编号：1000－6931（2015）08－1477－06

文献标志码：A

中图分类号：TL99