A Three-point Coupled Compact Integrated RBF Scheme for Second-order Differential Problems

C.M.T.Tien,N.Thai-Quang,N.Mai-Duy,C.-D.Tran and T.Tran-Cong

A Three-point Coupled Compact Integrated RBF Scheme for Second-order Differential Problems

C.M.T.Tien1,N.Thai-Quang1,N.Mai-Duy1,C.-D.Tran1and T.Tran-Cong1

In this paper,we propose a three-point coupled compact integrated radial basis function(CCIRBF)approximation scheme for the discretisation of second-order differential problems in one and two dimensions.The CCIRBF employs integrated radial basis functions(IRBFs)to construct the approximations for its first and second derivatives over a three-point stencil in each direction.Nodal values of the first and second derivatives(i.e.extra information),incorporated into approximations by means of the constants of integration,are simultaneously employed to compute the first and second derivatives.The essence of the CCIRBF scheme is to couple the extra information of the nodal first and second derivative values via their identity equations.Owing to its coupling of the information of the nodal first and second derivatives,the CCIRBF scheme becomes more accurate,stable and ef ficient than the normal compact integrated radial basis function(CIRBF)schemes proposed by[Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2012)].The main features of the CCIRBF scheme include:three-point,high-order accuracy,stability,ef ficiency and inclusion of boundary values.Several analytic problems are considered to verify the present scheme and to compare its accuracy,stability and ef ficiency with those of the CIRBF,higher-order compact finite difference(HOC)and some other high-order schemes.Numerical results show that highly accurate and stable results are obtained with the proposed scheme.Additionally,the present scheme also takes less time to achieve target accuracy in comparison with the CIRBF and HOC schemes.

Coupled compact integrated RBF(CCIRBF),three-point,higher-order compact finite difference(HOC),high-order scheme,Poisson equation,heat equation,Burgers equation,steady/unsteady convection-diffusion equation,alternating direction implicit(ADI).

1 Introduction

Considerable progress has been made over the past decades on developing highorder accuracy schemes for solving second-order differential equations.The traditional first-order upwind and second-order central finite difference(FD)methods have low rates of convergence and therefore require sufficiently fine meshes[Kun,Yang,and Zhang(2012)].The computational cost of those methods is thus relatively high,particularly for the case of high level of accuracy.One approach to alleviate these difficulties is to use high-order methods by which comparable accuracy can be obtained with much coarser discretisation.

Higher-order compact finite difference methods(HOC)[Hirsh(1975);Rubin and Khosla(1977);Adam(1977);Noye and Tan(1989)],which require fewer grid points,have been widely used in numerical calculations with high accuracy for the small scale problems.These approaches can provide a compromised way of combining the robustness of the FD and the accuracy of spectral-like methods which converge exponentially towards the exact solution as the number of nodes is increased.In the HOC methods,the derivative values at a particular node are implicitly computed not only from the function values but also from the values of the derivatives at the neighboring nodes.In comparison with the FD,these approaches give a higher order of accuracy for the same number of grid points,using a smaller stencil.Lele(1992)proposed a family of spectral-like compact formulations and generalised its resolution characteristics on a uniform grid.Since then,the compact schemes have attained wide popularity in solving various problems involving the convection-diffusion and Navier-Stokes equations[Spotz and Carey(1995);Mahesh(1998);Ma,Fu,Kobayashi,and Taniguchi(1999);Li and Tang(2001);Kalita,Dalal,and Dass(2002);Karaa and Zhang(2004);Tian and Ge(2007);Tian,Liang,and Yu(2011)].

Following the trend toward highly accurate numerical schemes for partial differential equations(PDEs),Kansa(1990a,b) first proposed the use of radial basis functions(RBFs)as approximants(here referred to as direct/differential RBF or DRBF methods).In the DRBF method,a closed form RBF approximating function is first obtained from a set of training points and the derivative functions are then calculated directly from the closed form RBF[Mai-Duy and Tran-Cong(2001a)].Mai-Duy and Tran-Cong(2001b,2003)afterward proposed the idea of using indirect/integrated radial basis functions(IRBFs)for the solution of PDEs.In the IRBF approach,the highest derivatives under interest are decomposed into a set of RBFs;and expressions for the lower derivatives and its function are then obtained through integration processes.Extensive numerical studies in[Mai-Duy and Tran-Cong(2001a,b,2003,2005)]have shown that the integral approach is more accurate than the differential approach because the integration process is averagely less sensi-tive to noise.The integration process gives rise to integration constants through which extra equations can be employed.A one-dimensional IRBF scheme has been developed in[Mai-Duy and Tanner(2007)].Global RBF schemes have advantages of fast convergence,meshless nature and simple implementation,however its RBF matrices are fully populated and thus tend to be much more ill-conditioned as the number of the RBF is increased.To resolve these drawbacks,Mai-Duy and Tran-Cong(2011)developed a five-point compact IRBF(here referred to as compact IRBF or CIRBF)scheme that is capable of solving second-order elliptic PDEs.Recently,Mai-Duy and Tran-Cong(2013)have proposed a three-point CIRBF scheme where only nodal values of second derivatives(i.e.extra information)are incorporated into the approximations.Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2012)has proposed another three-point CIRBF scheme where the extra information includes nodal values of the first and second derivatives for the computation of the first and second derivatives,respectively.The latter scheme was reported to be more accurate[Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2012)].Several other approaches using RBFs for solving engineering and science problems have been recently reported,see for example[Kosec,Zaloznik,Sarler,and Combeau(2011);Ngo-Cong,Mai-Duy,Karunasena,and Tran-Cong(2012);Sellountos,Polyzos,and Atluri(2012);Mramor,Vertnik,and Sarler(2013);Thai-Quang,Mai-Duy,C.-D.Tran,and Tran-Cong(2013);Elgohary,Dong,Junkins,and Atluri(2014a,b);Hon,Sarler,and Dong(2015)]and the references therein.

This article develops a new three-point coupled compact integrated radial basis function(CCIRBF)scheme for solving second-order PDEs.In the proposed CCIR BF scheme,the first and second derivatives at a particular node are implicitly and simultaneously obtained from the function values at the stencil points and from the nodal values of not only first but also second derivatives(i.e.extra information)at two neighboring points.Coupling processes of the extra information of the nodal first and second derivatives are performed by means of coupling identity equations.The CCIRBF scheme is more accurate,stable and ef ficient than the normal CIRBF schemes developed in[Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2012)],which is achieved by the coupling of the first and second derivatives.Major features of the CCIRBFschemeare:three-point,implicit,high-orderaccuracy,stability,efficiency and inclusion of boundary values.Numerical solutions of PDEs,including Poisson equation,heat equation,Burgers equation,and steady/non-steady convectiondiffusion equations,are used to illustrate the accuracy,stability and efficiency of the proposed CCIRBF scheme.Results obtained are also compared with those obtained by the CIRBF,HOC and some other high-order schemes.Greater accuracy and stability are obtained with the present scheme.Furthermore,it also achieves prescribed accuracy with smaller amount of time compared with the CIRBF and HOC schemes.The proposed CCIRBF scheme appears to be an attractive alternative to the normal CIRBF scheme for computations of second-order PDEs.

The remainder of this paper is organised as follows:the CCIRBF scheme is proposed in Section 2.Section 3 outlines the ADI solution for convection-diffusion equations.In Section 4,numerical examples are presented and CCIRBF results are compared with some published solutions,where appropriate.Finally,concluding remarks are given in Section 5.

2CCIRBF scheme

To improve the performance of compact local approximations,a coupled compact integrated radial basis function(CCIRBF)scheme is developed in this paper as follows.

Consider a two-dimensional domain Ω,which is represented by a uniform Cartesian grid.The nodes are indexed in the x-direction by the subscript i(i∈{1,2,...,nx})and in y-direction by j(j∈{1,2,...,ny}).For rectangular domain,let N be the total number of nodes(N=nx×ny)and Nipbe the number of interior nodes(Nip=(nx-2)×(ny-2)).At an interior grid pointwhere i∈ {2,3,...,nx-1}and j∈ {2,3,...,ny-1},the associated stencils to be considered here are two local stencils:in the x-direction andin the y-direction.Hereafter,for brevity,η denotes either x or y in a generic local stencil{η1,η2,η3},where η1＜ η2＜ η3and η2≡η(i,j),are illustrated in Figure 1.

Figure 1:Compact three-point 1D-IRBF stencil for interior nodes.

The integral approach starts with the decomposition of second derivatives of a variable,u,into RBFs

where m is taken to be 3 for local stencils;is the set of RBFs;andthe set of weights/coefficients to be found.Approximate representations for the first derivatives and the functions itself are then obtained through the inte-gration processes

2.1 First derivatives at interior nodes

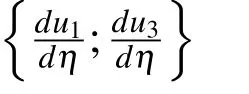
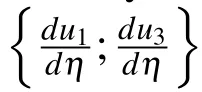
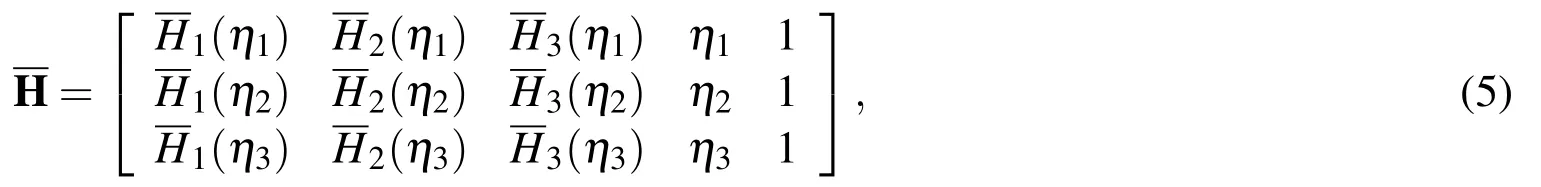
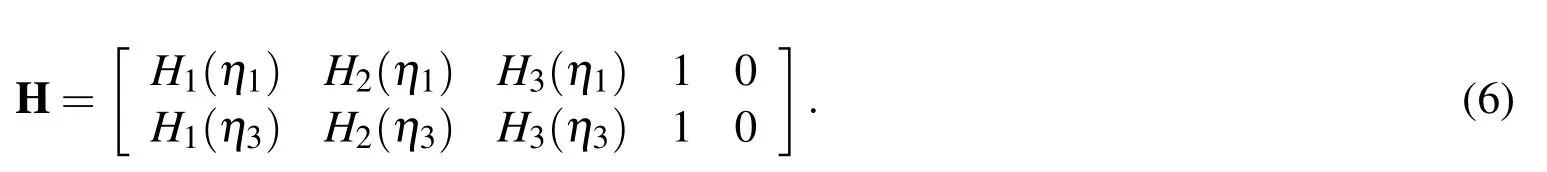
Solving(4)yields

which maps the vector of nodal values of the function and first derivative to the vector of RBF coefficients including the two integration constants.Approximate expressions for the first derivative in the physical space are obtained by substituting(7)into(2)

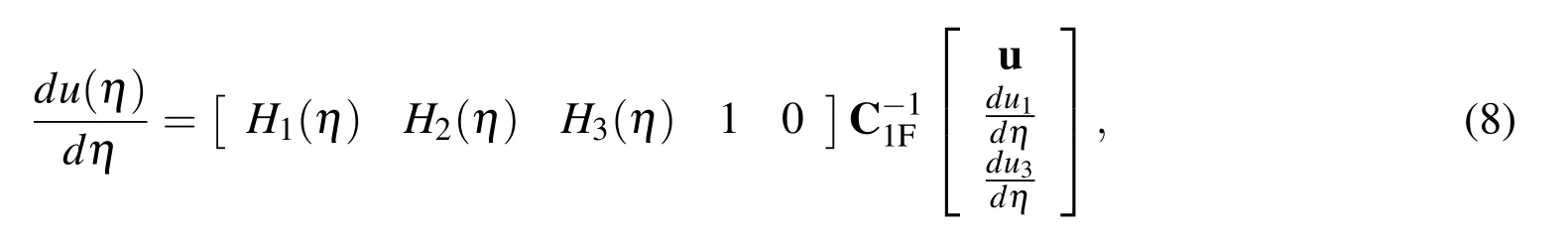
where η1≤ η ≤ η3andu=[u1,u2,u3]T.(8)can be rewritten as

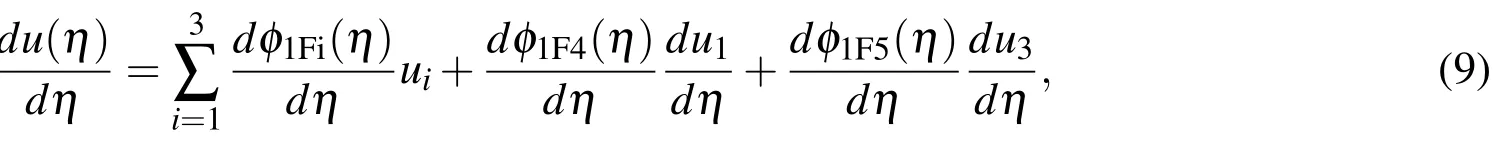
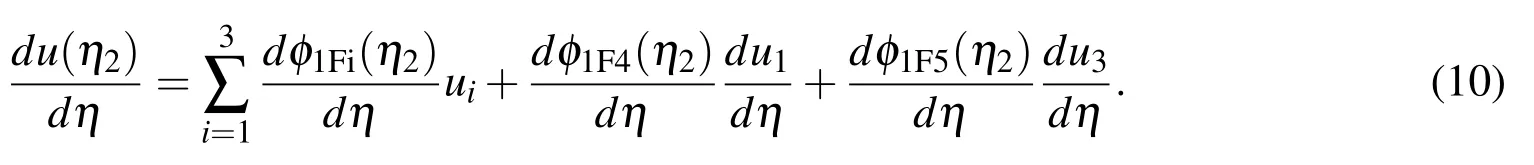
For brevity,we rewrite expression(10)as

where the nodal values of the first derivatives on the right hand side are treated as unknowns.Rearranging(12)in the matrix-vector form

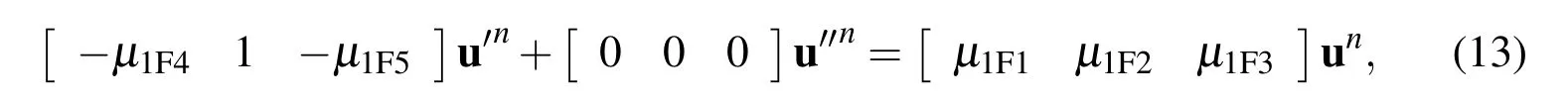
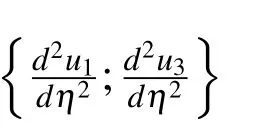
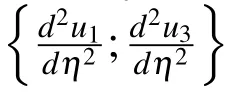
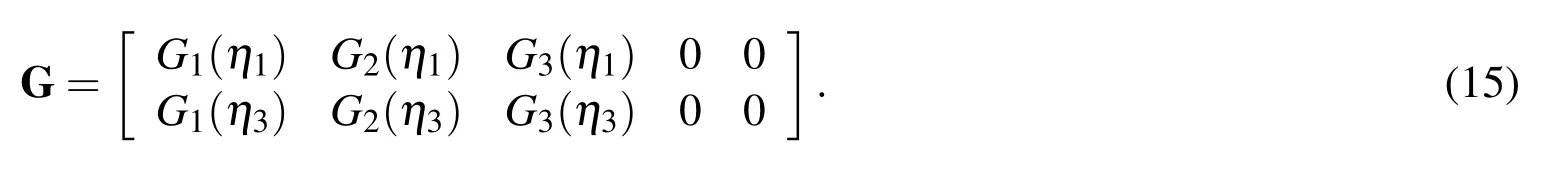
Solving(14)yields

which maps the vector of nodal values of the function and second derivative to the vector of RBF coefficients including the two integration constants.Approximate expressions for the first derivative in the physical space are obtained by substituting(16)into(2)

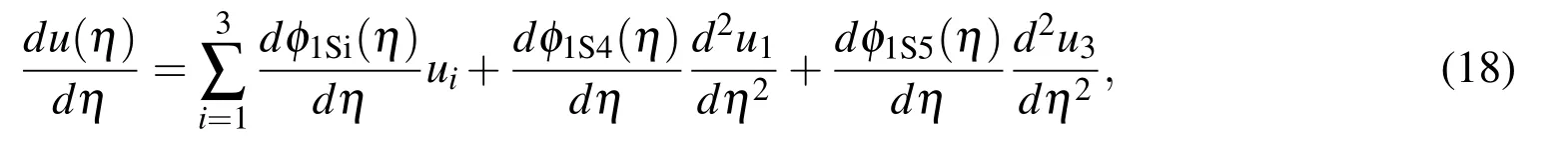
For brevity,we rewrite expression(19)as

where the nodal values of the second derivatives on the right hand side are treated as unknowns.Rearranging(21)in the matrix-vector form

where

2.1.3 First derivative couplings at interior nodes

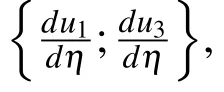
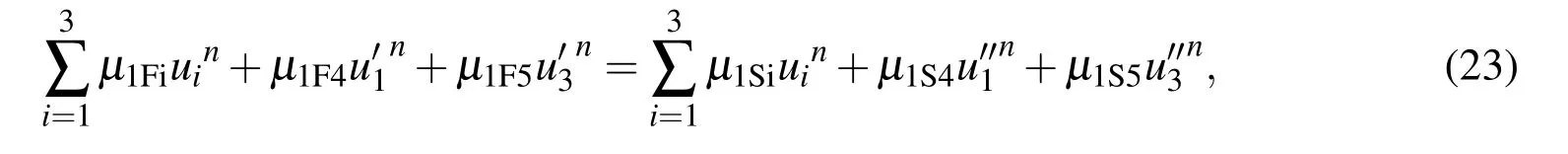
or in the matrix-vector form

where.

2.2 First derivatives at boundary nodes

At the boundary nodes,the first derivatives are approximated in special compact stencils.Consider the boundary node,e.g.η1.Its associated stencil is{η1,η2,η3,η4}as shown in Figure 2.For the coupled compact approximation of the first derivative at the boundary node η1,nodal derivative values(i.e.extra information)are chosen as bothandThe approximation is processed through three steps:(i)we first approximate its first derivative over its associated four-point stencil involvingwe then approximate its first derivative over the same stencil used in step(i)involving(iii)an identity equation of the first derivative is introduced to incorporate bothandinto the first derivative approximation.

Figure 2:Special compact four-point 1D-IRBF stencil for boundary nodes.

2.2.1 First derivatives at boundary node η1involving

We construct a conversion system over the special four-point stencil associated with the boundary node η1involvingin the form

whereCsp1Fis the conversion matrix andare de fined as

Solving(25)yields

The boundary value of the first derivative is thus obtained by substituting(28)into(2)and taking η = η1

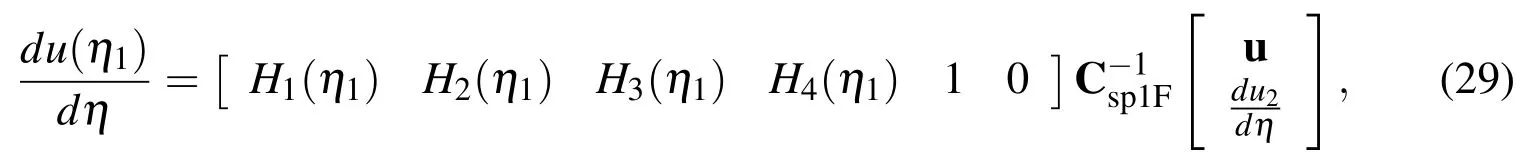
where(29)can be rewritten as

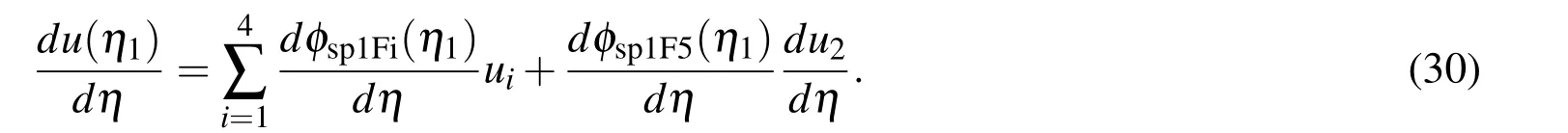
For brevity,we rewrite expression(30)as

where the nodal value of the first derivative on the right hand side is treated as unknowns.Rearranging(32)in the matrix-vector form

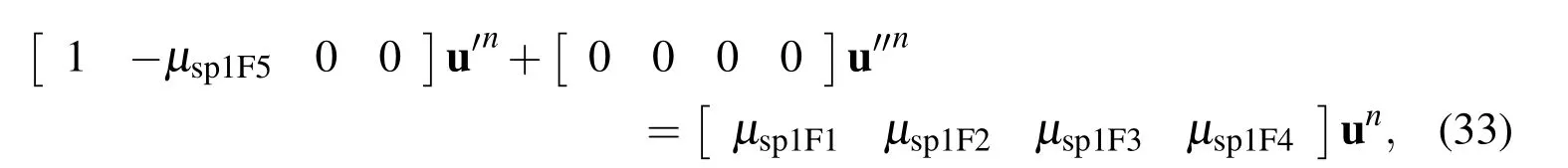
where

2.2.2 First derivatives at boundary node η1involving

We construct a conversion system over the special four-point stencil associated with the boundary node η1involvingin the form

whereCsp1Sis the conversion matrix;Hspis de fined as before,i.e.(26),andGspis de fined as

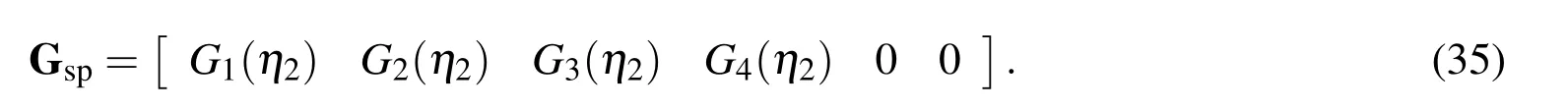
Solving(34)yields

The boundary value of the first derivative is thus obtained by substituting(36)into(2)and taking η = η1

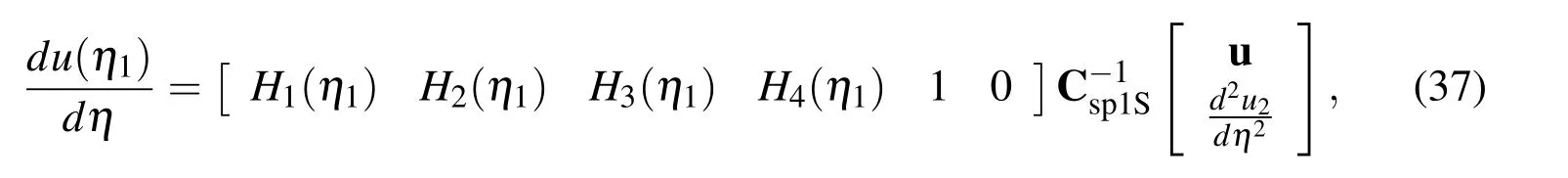
whereu=[u1,u2,u3,u4]T.(37)can be rewritten as

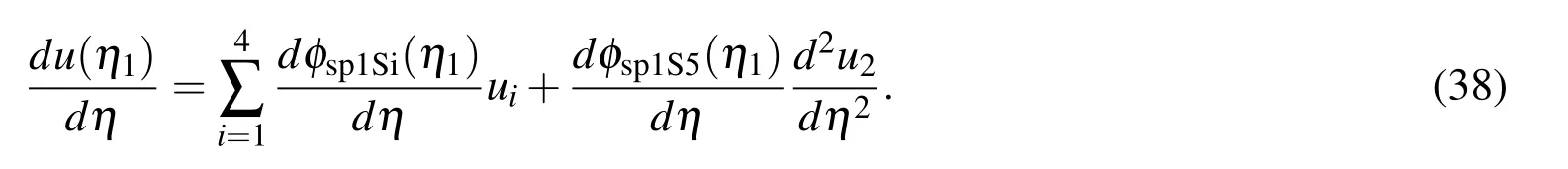
For brevity,we rewrite expression(38)as

where the nodal value of the second derivative on the right hand side is treated as unknowns.Rearranging(40)in the matrix-vector form

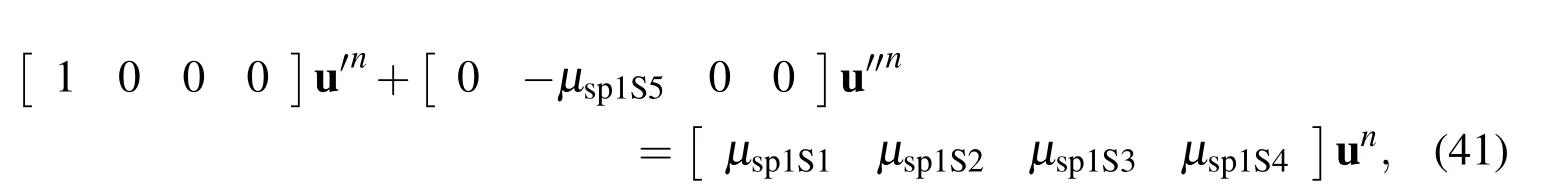
where

2.2.3 First derivative coupling at boundary node η1

For the first derivative coupling at each boundary node,e.g.η=η1,we set the right hand side of(31)to be equal to that of(39)to couple the nodal first derivative information,i.e.and the nodal second derivative information,i.e.,as follows.

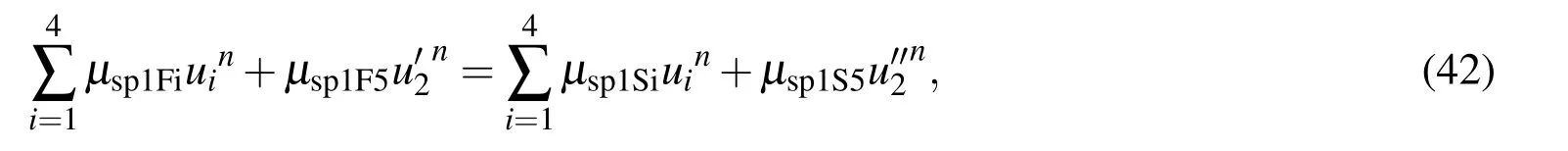
or in the matrix-vector form

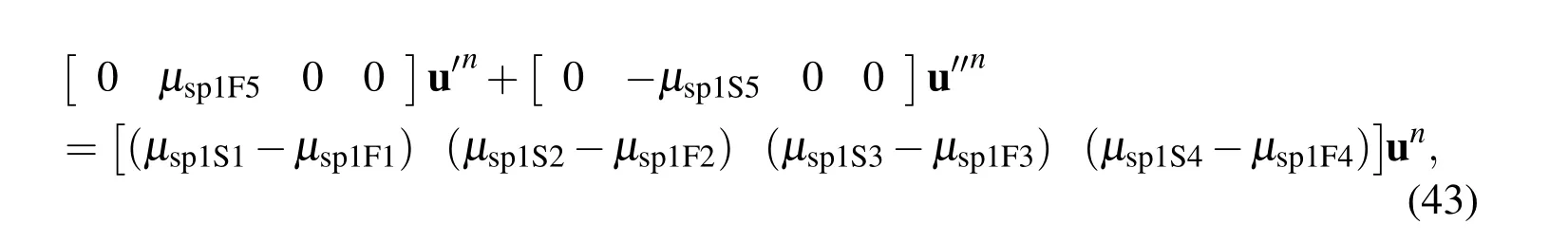
where

In a similar manner,one is able to calculate the first derivative at the boundary node ηnη.

2.3 Second derivatives at interior nodes

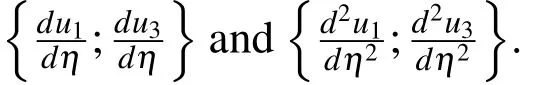
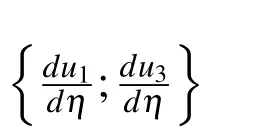
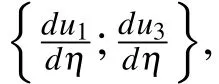
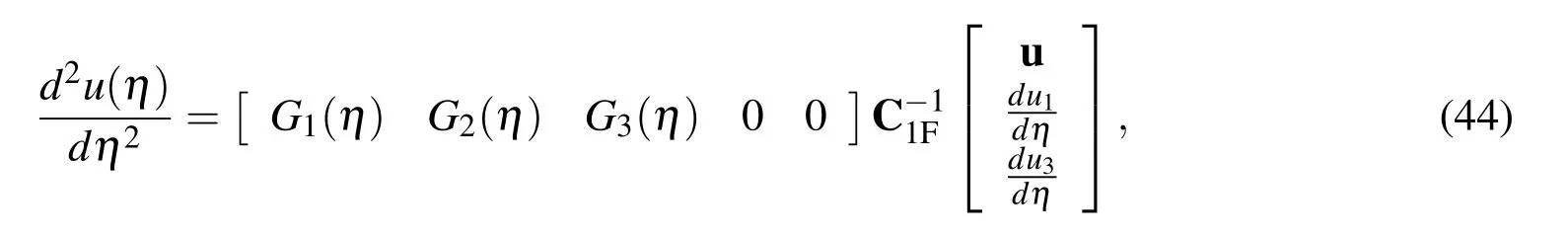
where η ∈ {η1,η2,η3}andu=[u1,u2,u3]T.(44)can be rewritten as

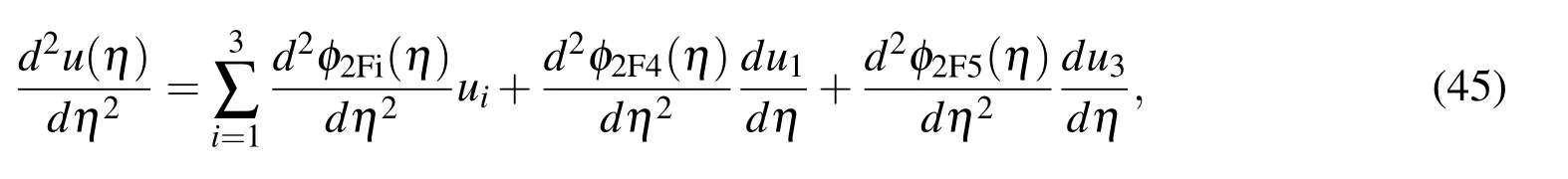
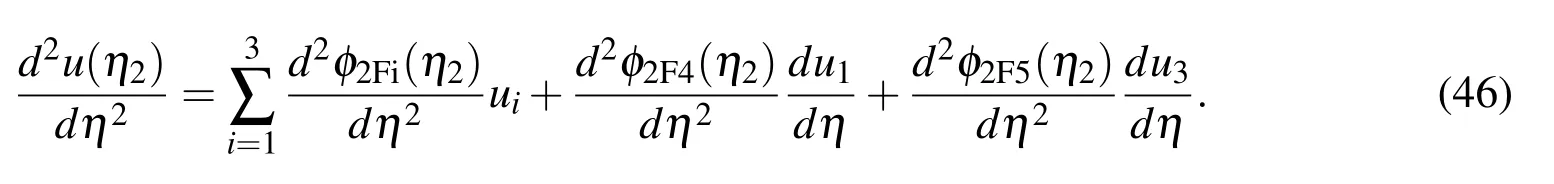
For brevity,we rewrite expression(46)as

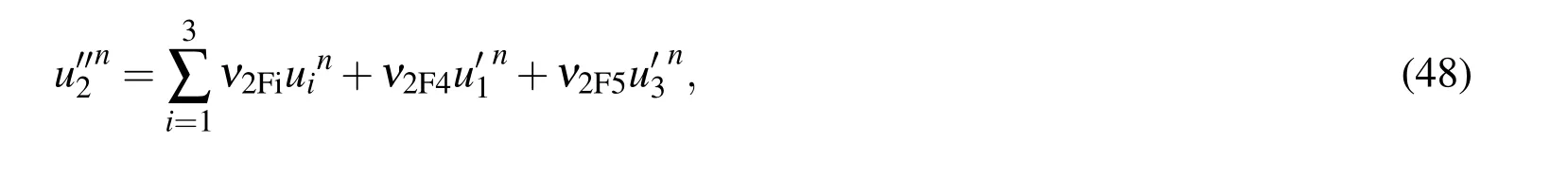
where the nodal values of the first derivatives on the right hand side are treated as unknowns.Rearranging(48)in the matrix-vector form

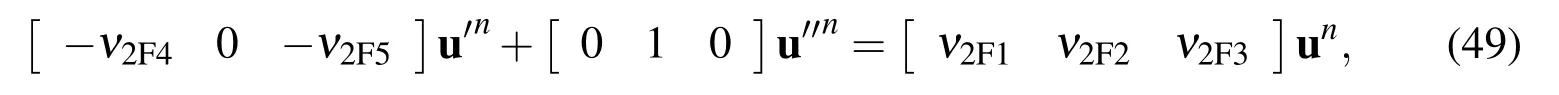
where

2.3.2 Second derivatives at interior nodes involving

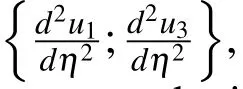
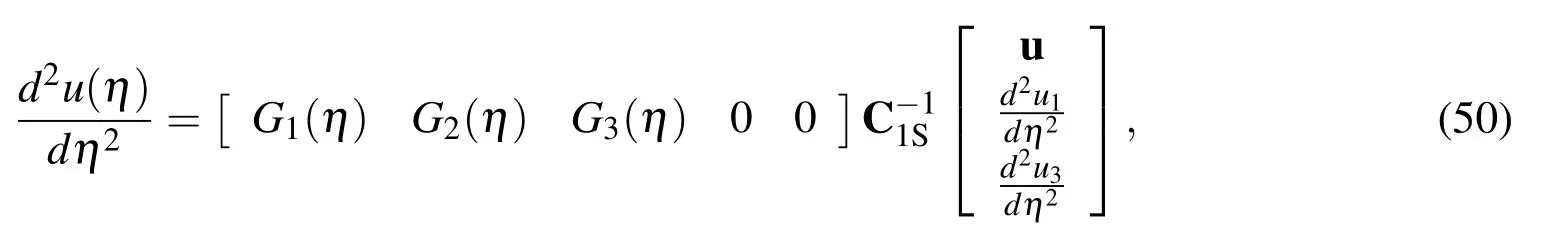
where η1≤ η ≤ η3andu=[u1,u2,u3]T.(50)can be rewritten as

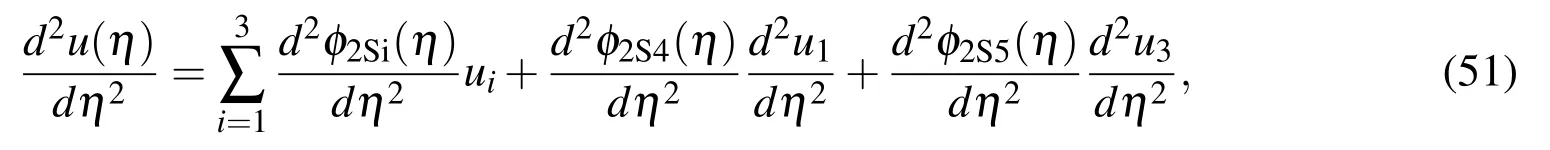
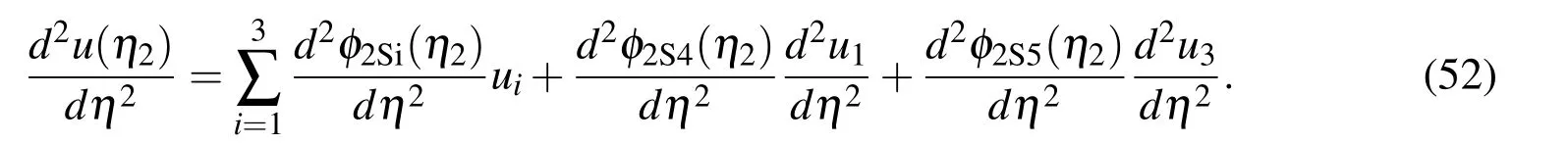
For brevity,we rewrite expression(52)as

where the nodal values of the second derivatives on the right hand side are treated as unknowns.Rearranging(54)in the matrix-vector form

where

2.3.3 Second derivative couplings at interior nodes

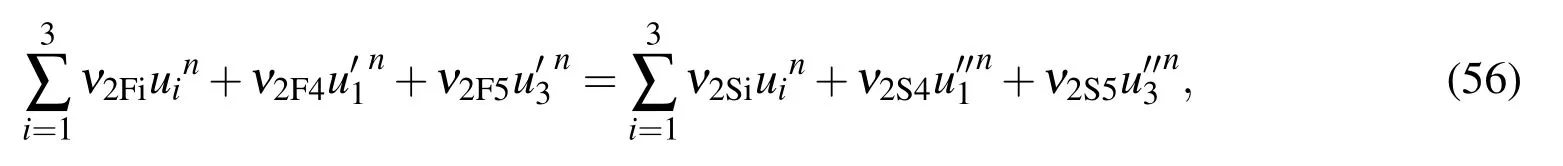
or in the matrix-vector form

where

2.4 Second derivatives at boundary nodes

At the boundary nodes,the second derivatives are approximated in special compact stencils.Consider the boundary node,e.g.η1.Its associated stencil is{η1,η2,η3,η4}as shown in Figure 2.For the coupled compact approximation of the second derivative at the boundary node η1,nodal derivative values(i.e.extra information)are chosen to be the same as those used for the approximation of the first derivatives,i.e.andThe approximation of its second derivative is processed through three steps:(i)we first approximate its second derivative over its associated four-point stencil involving;(ii)we then approximate its second derivative over the same stencil used in step(i)involvingiii)an identity equation of the second derivative is introduced to incorporate bothandinto the second derivative approximation.

2.4.1 Second derivatives at boundary node η1involving

Because we employ the same extra information used in the approximation of the first derivatives involving,approximate expression for the second derivative at η1in the physical space is obtained by simply substituting(28)into(1)and taking η=η1

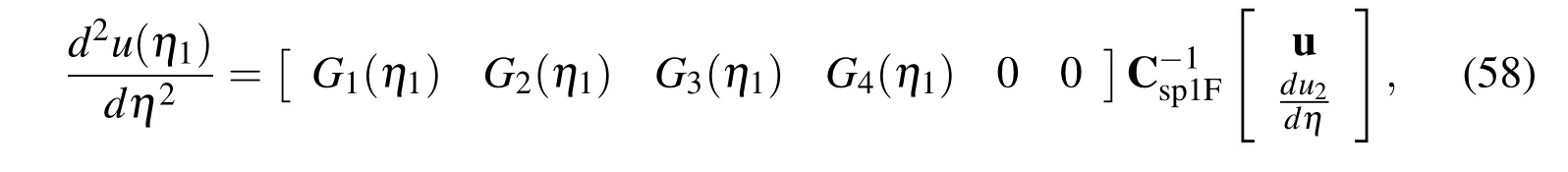
where(58)can be rewritten as

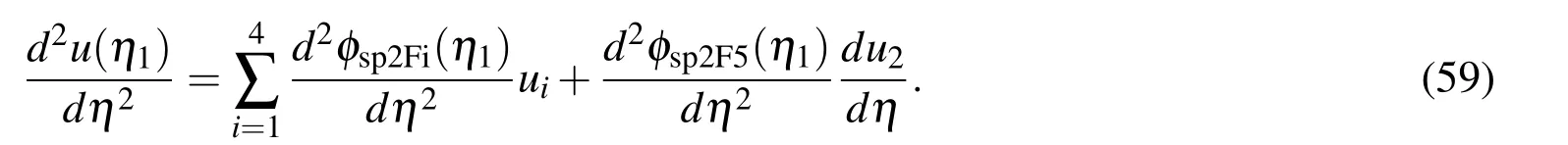
For brevity,we rewrite expression(59)as

where the nodal value of the first derivative on the right hand side is treated as unknowns.Rearranging(61)in the matrix-vector form

where

2.4.2 Second derivatives at boundary node η1involving

Because we employ the same extra information used in the approximation of the first derivatives involvingapproximate expression for the second derivative at η1in the physical space is obtained by simply substituting(36)into(1)and taking η=η1

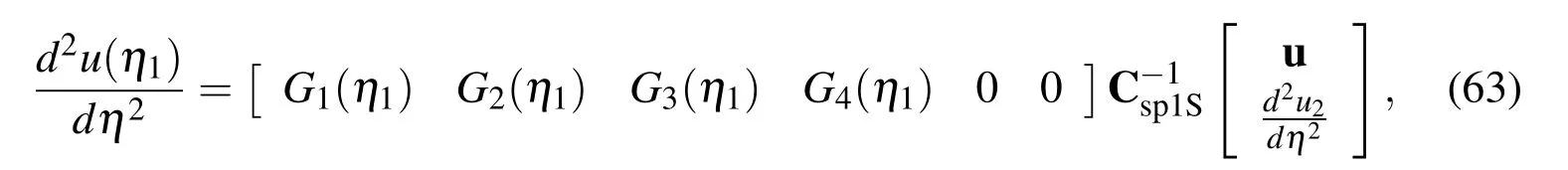
whereu=[u1,u2,u3,u4]T.(63)can be rewritten as

For brevity,we rewrite expression(64)as

where the nodal value of the second derivative on the right hand side is treated as unknowns.Rearranging(66)in the matrix-vector form

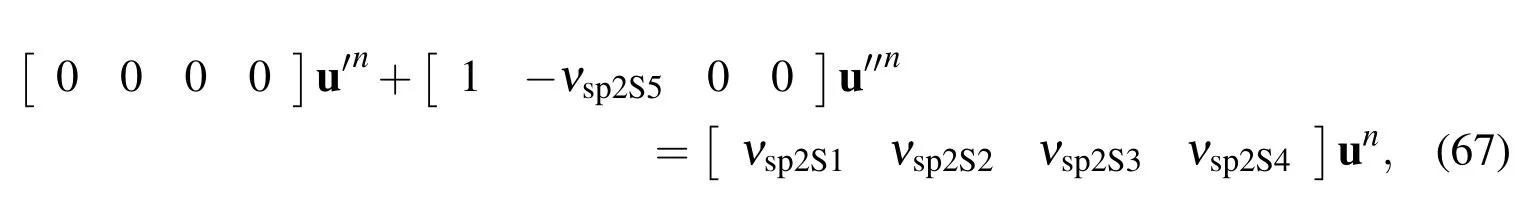
where

2.4.3 Second derivative coupling at boundary node η1

For the second derivative coupling at each boundary node,e.g.η=η1,we set the right hand side of(60)to be equal to that of(65)to couple the nodal first derivative information,i.e.and the nodal second derivative information,i.e.as follow

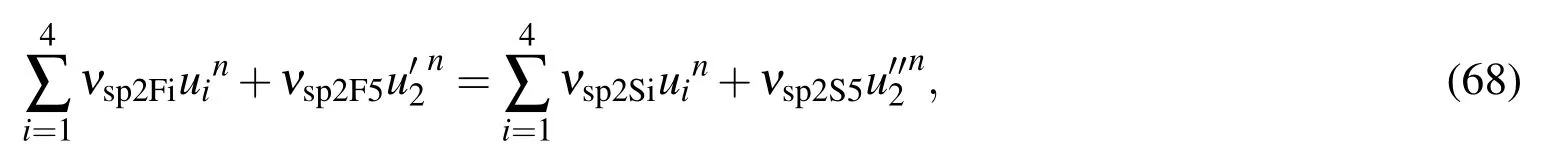
or in the matrix-vector form

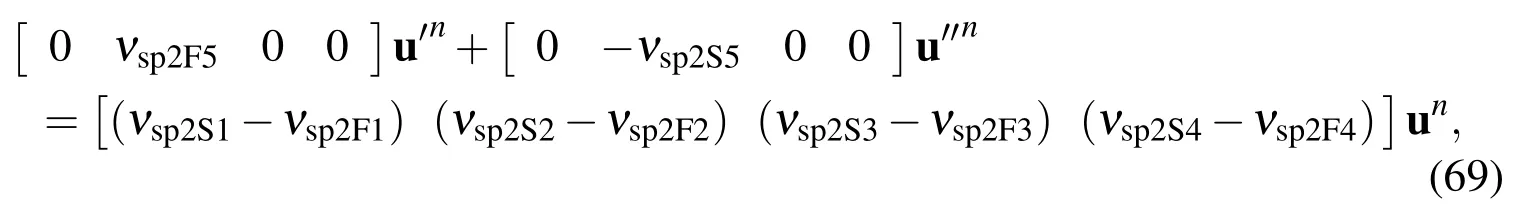
where

In a similar manner,one is able to calculate the second derivative at the boundary node ηnη.

2.5 Matrix assembly for first and second derivative expressions

The IRBF system on a grid line for the first derivative is obtained by letting the interior node taking values from 2 to(nη-1)in(13),(22),and(24);and,making use of(33),(41),and(43)for the boundary nodes 1 and nη.In a similar manner,the IRBF system on a grid line for the second derivative is obtained by letting the interior node taking values from 2 to(nη-1)in(49),(55),and(57);and,making use of(62),(67),and(69)for the boundary nodes 1 and nη.The resultant matrix assembly is expressed as

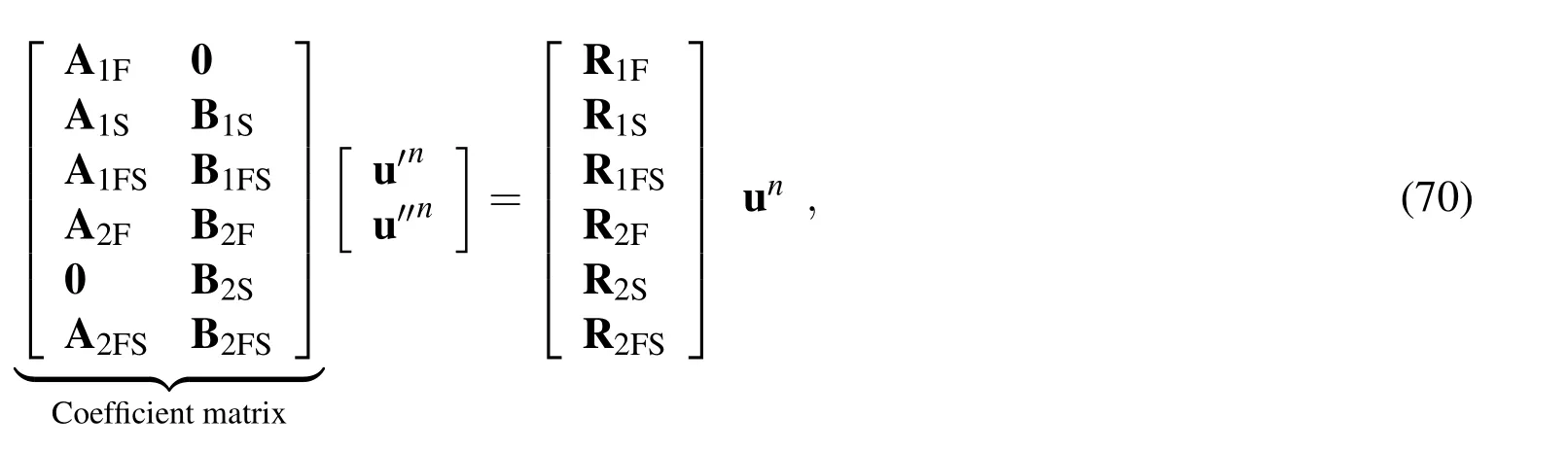
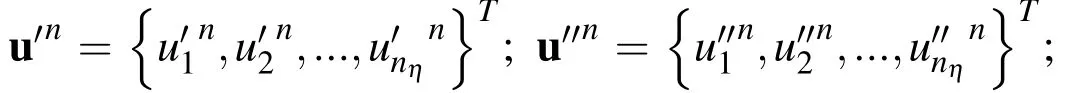
whereDηandDηηare nη×nηmatrices.

It is noted that,for brevity,we use the same notations to represent the RBF coefficients for the approximation of first and second derivatives.In fact,for example,the coefficient set[w1,w2,w3,c1,c2]Tin(4)is not the same as that in(14).

3 ADI method for convection-diffusion equations

We consider a two-dimensional(2D)unsteady convection-diffusion equation for a variable u

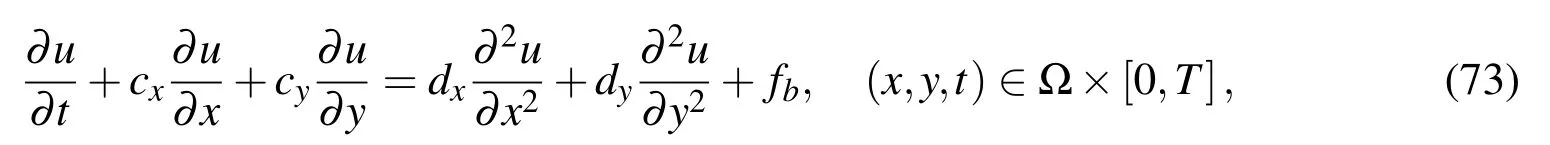
subject to the initial condition

and Dirichlet boundary condition

where Ω is a two-dimensional rectangular domain;Γ is the boundary of Ω;[0,T]is the time interval;fbis the driving function;u0and uΓare some given functions.In(73),cxand cyare the convective velocities,and dxand dyare the positive diffusive coefficients.For the steady-state case,(73)reduces to

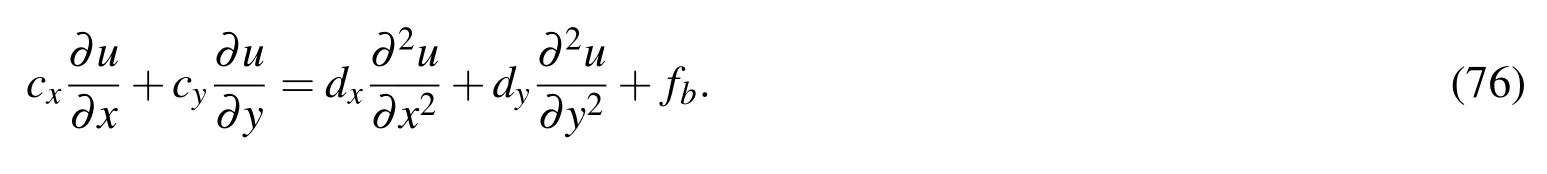
(73)and(76)are known as a simplified version of the Navier-Stokes equation.They have been widely used in computational fluid dynamics(CFD)and physical sciences to describe the transport of mass,momentum,vorticity,heat and energy,the modeling of semiconductors,etc.In this article,we implement the alternating direction implicit(ADI)method proposed by You(2006)in the context of CCIRBF approximations for the solution of the convection-diffusion equation.

3.1 You’s ADI temporal discretisation

You(2006)proposed the following ADI factorisation to(73)

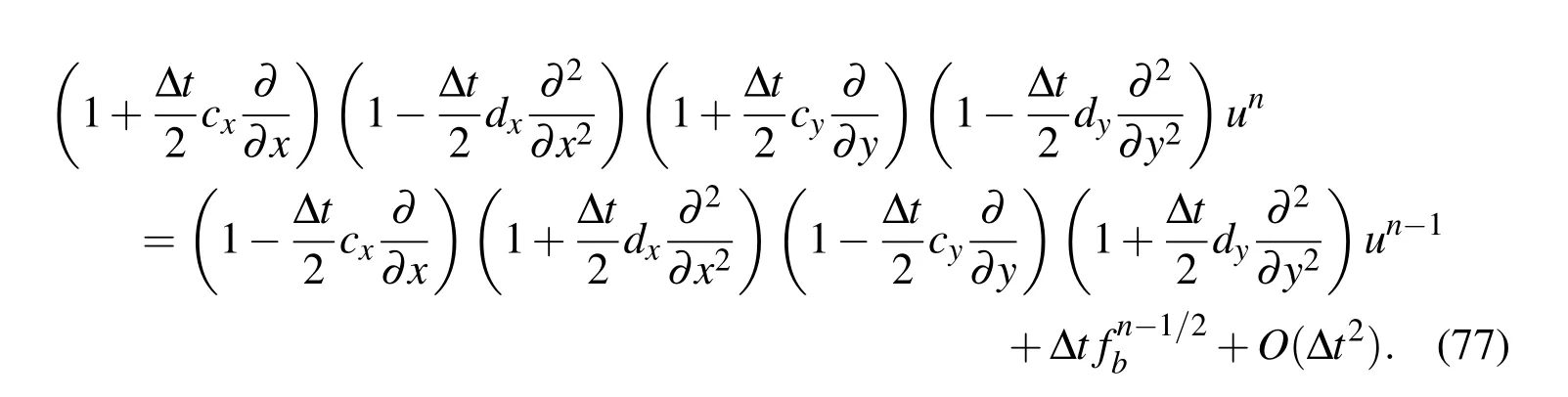
We rewrite(77)

where

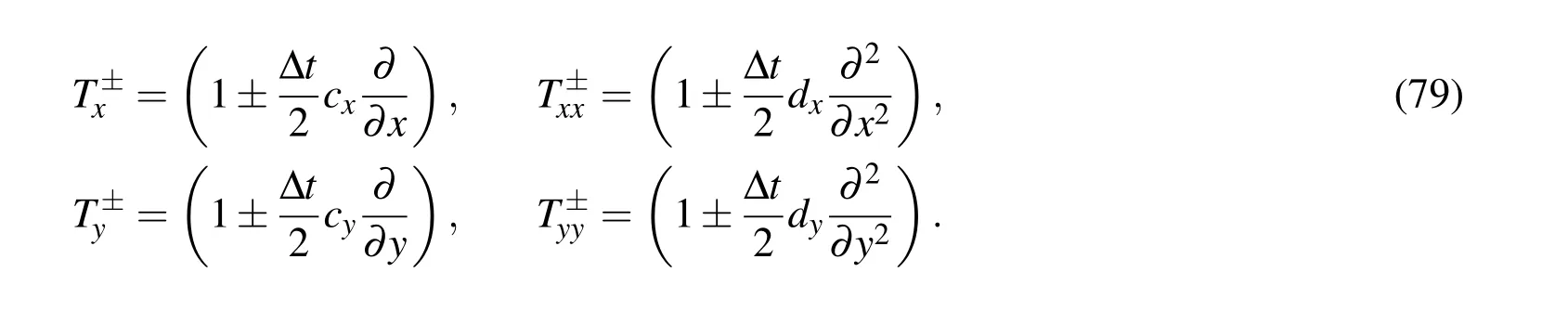
(78)can be solved by the following two steps

3.2 ADI spatial-temporal discretisation

We incorporate the CCIRBF approximations derived in Section 2 into the ADI equation by substituting(71)and(72),nodal value of the first and second derivatives,into(77),resulting in the matrix-vector form

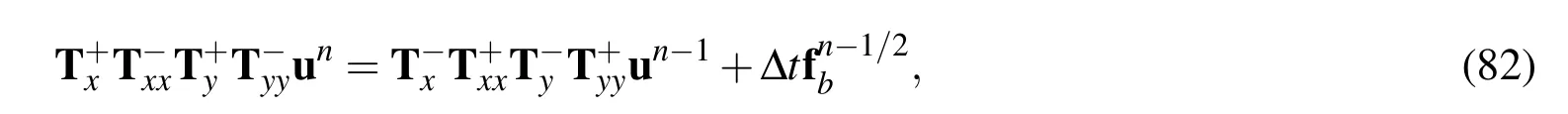
where

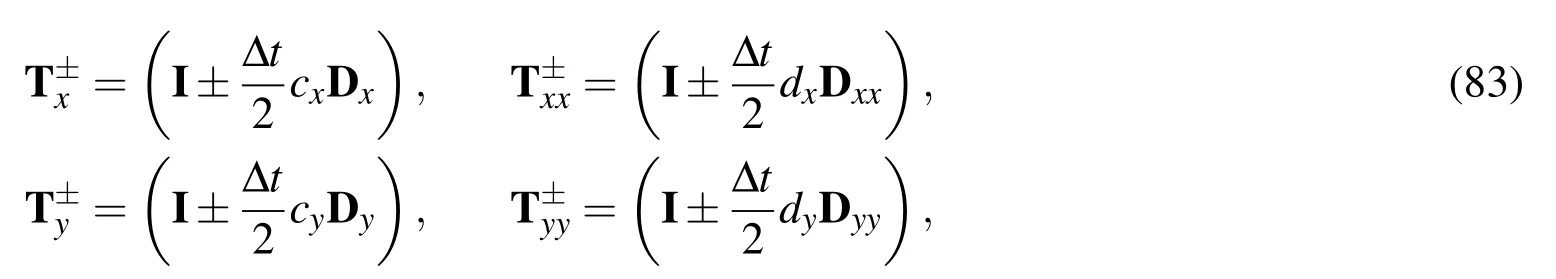
andIis the nη×nηidentity matrix.

3.3 ADI calculation procedure

Equation(82)is equivalent to

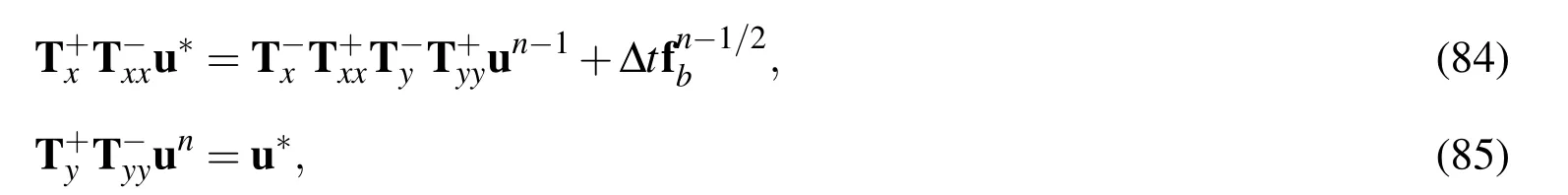
which can be solved by the following two steps.

Step 1:This step involves two sub-steps

·Sub-step 1:Compute the nodal values ofu∗at the left and right boundaries of the computational domain via(85)for x=x1and x=xnxwith the given boundary condition(75).

·Sub-step 2:Solve(84)on the x-grid lines(y=yj,j∈ {2,3,···,ny-1})for

the values ofu∗at the interior nodes.

Step 2:Solve(85)on the y-grid lines(x=xi,i∈ {2,3,···,nx-1})for the values ofunat the interior nodes.

4 Numerical examples

We choose the multiquadric(MQ)function as the basis function in the present calculations

where ciand aiare the centre and the width of the i-th MQ,respectively.For each stencil,the set of nodal points is taken to be the same as the set of MQ centres.We simply choose the MQ width as ai= βhi,where β is a positive scalar and hiis the distance between the i-th node and its closest neighbour.The value of β=50 is employed in the present work.We evaluate the performance of the present scheme through the following measures

i.the root mean square error(RMS)is de fined as

where fiand fiare the computed and exact values of the solution f at the i-th node,respectively;and,N is the number of nodes over the whole domain.

ii.the average absolute error(L1)is de fined as

iii.the maximum absolute error(L∞)is de fined as

iv.the global convergence rate with respect to the grid re finement is de fined through

v.a solution is considered to reach its steady state when

In this work,calculations are done with a Dell computer Optiplex 9010 version 2013.Its specifications are intel(R)core(TM)i7-3770 CPU 3.40 GHz 3.40 GHz,memory(RAM)of 8GB(7.89 usable)and 64-bit operating system.The Matlab(R)version 2012 is utilised.

4.1 Poisson equation

In order to study the spatial accuracy of the present CCIRBF approximation scheme,we consider the following Poisson equation

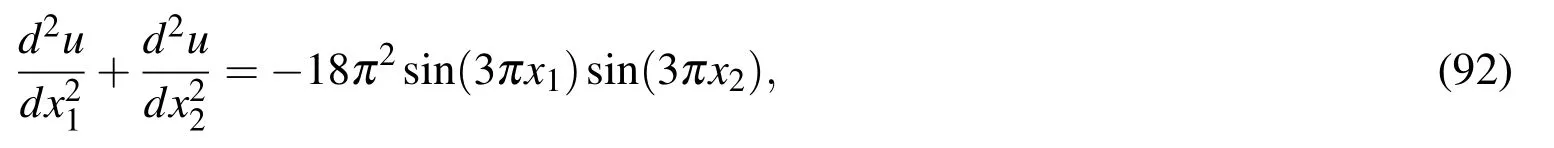
on a square domain[0,1]2,subjected to Dirichlet boundary condition derived from the following exact solution

The calculations are carried out on a set of uniform grids of{21×21,31×31,...,111×111}.Table 1 shows that the proposed scheme outperforms the HOC and CIRBF schemes in terms of solution accuracy.Figure 3 illustrates the matrix condition number grows with approximately the rate of O(h-2.00)for the HOC and CIRBF,and O(h-1.90)for the CCIRBF.

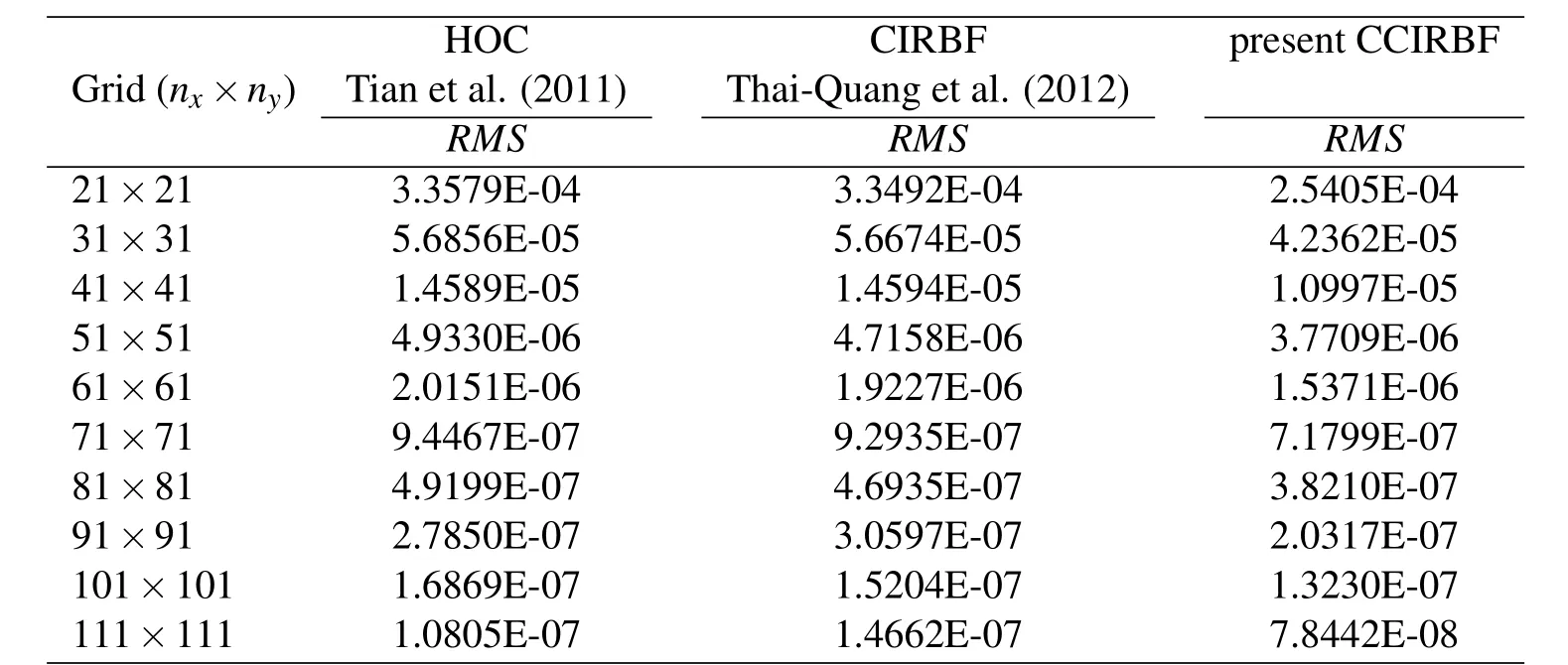
Table 1:Poisson equation:The effect of grid size h on the solution accuracy RMS.

To compare the computational efficiency of the CCIRBF,CIRBF and HOC schemes,we let the grid increase as{21×21,23×23,...}until the solution accuracy achieves a target RMS level of 10-6.Figure 4 shows that the present scheme takes much less time to reach the target accuracy than the CIRBF and HOC.It is noted that the final grid used to achieve the target accuracy is 71×71 for the HOC and CIRBF and 67×67 for the CCIRBF.

The effect of the MQ width on the solution accuracy for three different grids{21×21,51×51,81×81}is illustrated in Figure 5.It can be seen that the present scheme has better accuracy and is more stable than the CIRBF scheme.

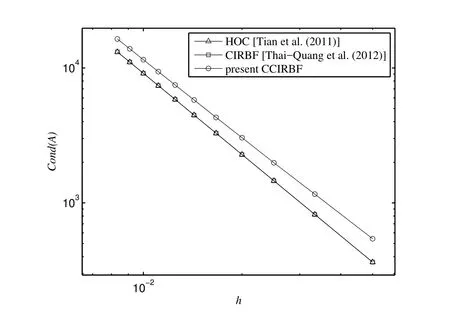
Figure 3:Poisson equation,{21×21,31×31,...,111×111}:The effect of grid size h on the matrix condition number.It is noted that the curves for the HOC-ADI and CIRBF-ADI are indistinguishable.

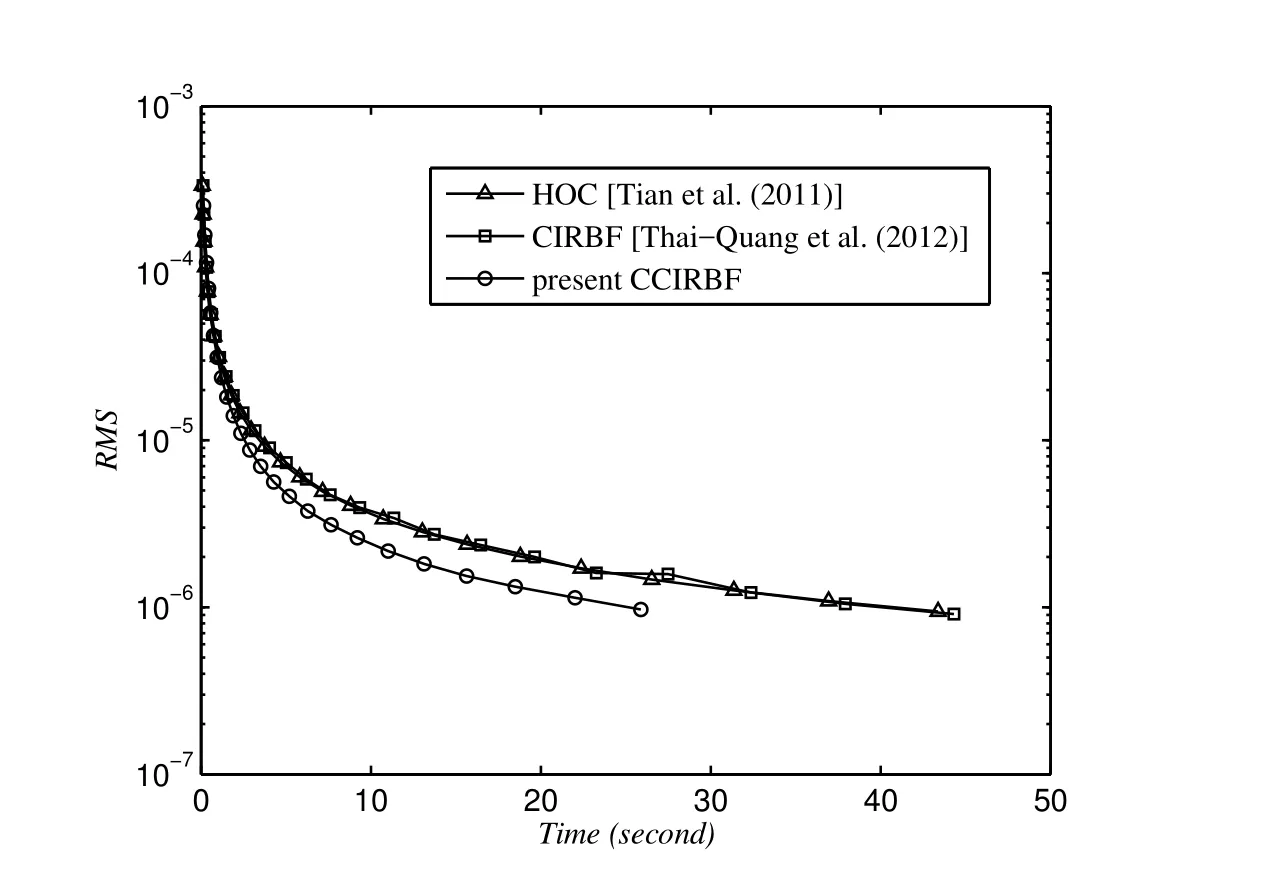
Figure 4:Poisson equation,{21×21,23×23,...}:The computational cost to achieve the target accuracy of 10-6.The final grid is 71×71 for the HOC and CIRBF and 67×67 for the CCIRBF.

Figure 5:Poisson equation,{21×21,51×51,81×81}:The effect of the MQ width β on the solution accuracy RMS.

4.2 Heat equation

By selecting the following heat equation,the performance of the proposed scheme can be studied for the diffusive term only as

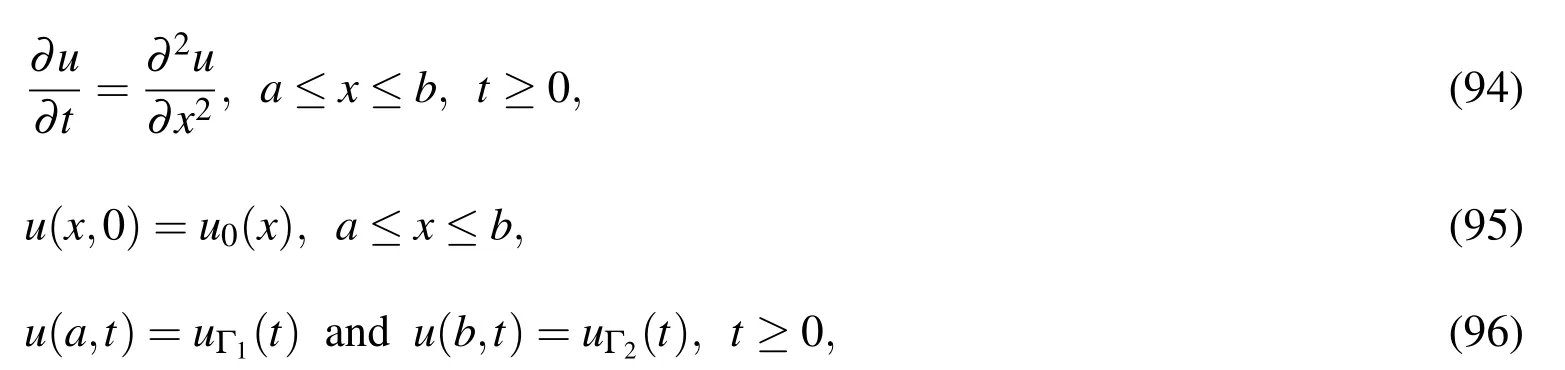
where u and t are the field variable and time,respectively;and u0(x),uΓ1(t),and uΓ2(t)are prescribed functions.The temporal discretisation of(94)with a Crank-Nicolson scheme gives

where the superscript n denotes the current time step.(97)can be rewritten as

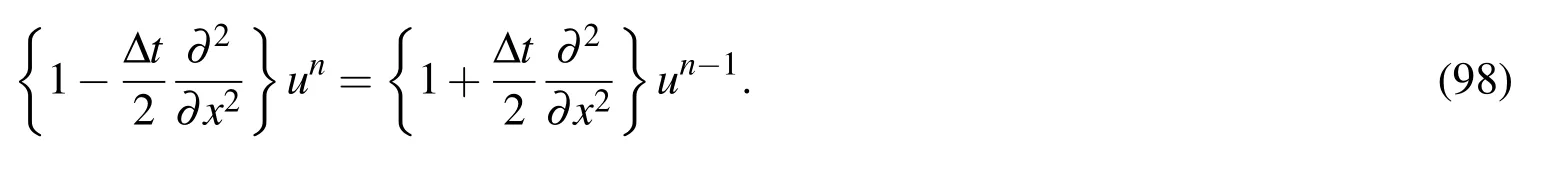
Consider(94)on a segment[0,π]with the initial and boundary conditions u(x,0)=sin(2x),0＜x＜π and u(0,t)=u(π,t)=0,t≥0,respectively.The exact solution of this problem can be veri fied to beThe spatial accuracy of the proposed scheme is tested on various uniform grids{11,21,...,111}.We employ here a small time step,Δt=10-6,to minimise the effect of the approximation error in time.The solution is computed at t=0.0125.Table 2 shows that the CCIRBF outperforms the HOC and CIRBF in terms of both solution accuracy and convergence rate.At the two finest grids,it can be seen that the CCIRBF maintains its high convergence rates and produces highly accurate and stable results while the convergence rates of the CIRBF fall dramatically.Figure 6 illustrates a similar trend of the matrix condition number for the three schemes.

Table 2:Heat equation,Δt=10-6,t=0.0125:The effect of grid size h on the solution accuracy RMS.LCR stands for"Local Convergence Rate".

To study the computational efficiency of the CCIRBF,CIRBF and HOC schemes,we increase the number of grids as{11,13,...}until the solution accuracy achieves a target RMS level of 10-6.We also use a small time step,Δt=10-6and the solution is computed at t=0.0125.Figure 7 shows that the present scheme uses a smaller amount of time to reach the target accuracy than the CIRBF and HOC.It is noted that the final grid used to achieve the target accuracy is 43 for the HOC and CIRBF and 41 for the CCIRBF.The effect of the MQ width on the solution accuracy for three different grids{11,41,71}is illustrated in Figure 8 where it can be observed that the present scheme has better accuracy than the CIRBF scheme.

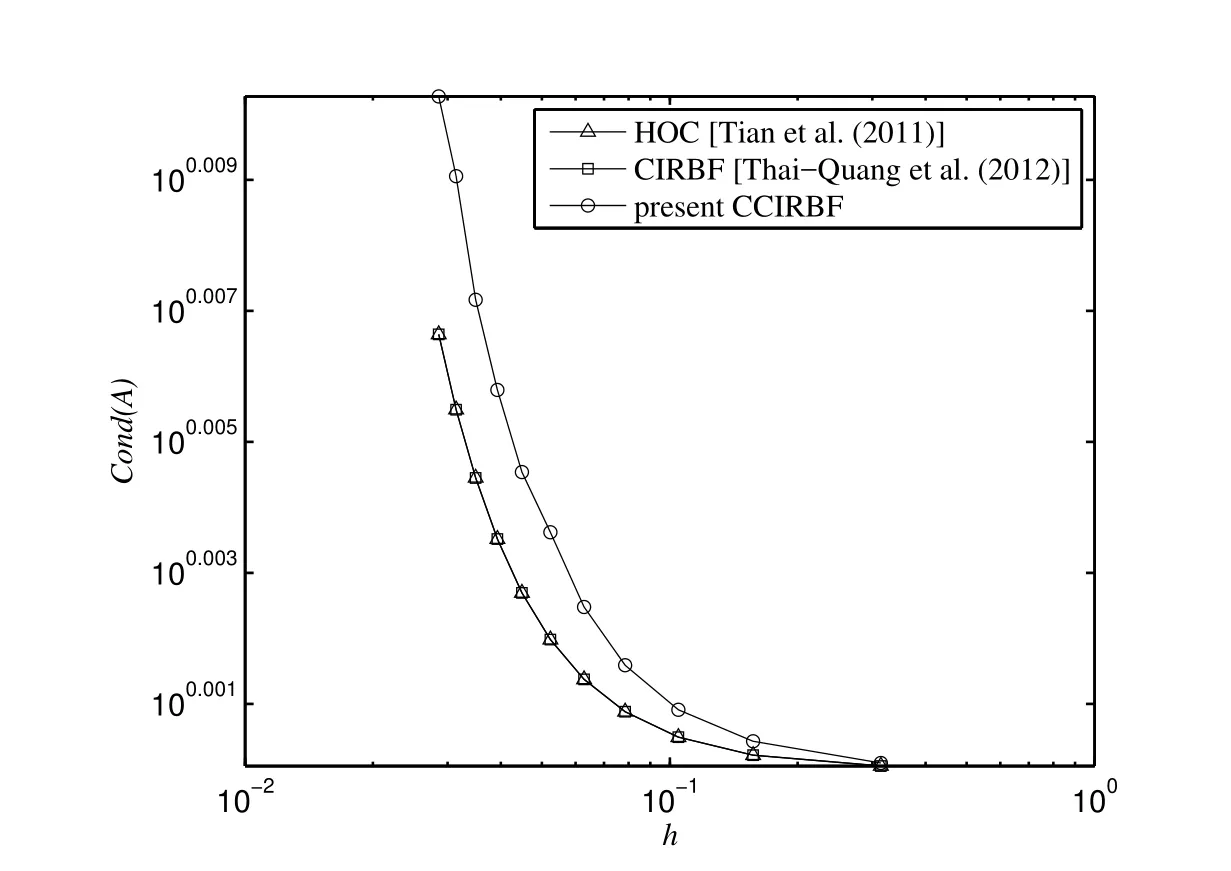
Figure 6:Heat equation,{11,21,...,111},Δt=10-6,t=0.0125:The effect of grid size h on the matrix condition number.It is noted that the curves for the HOC-ADI and CIRBF-ADI are indistinguishable.

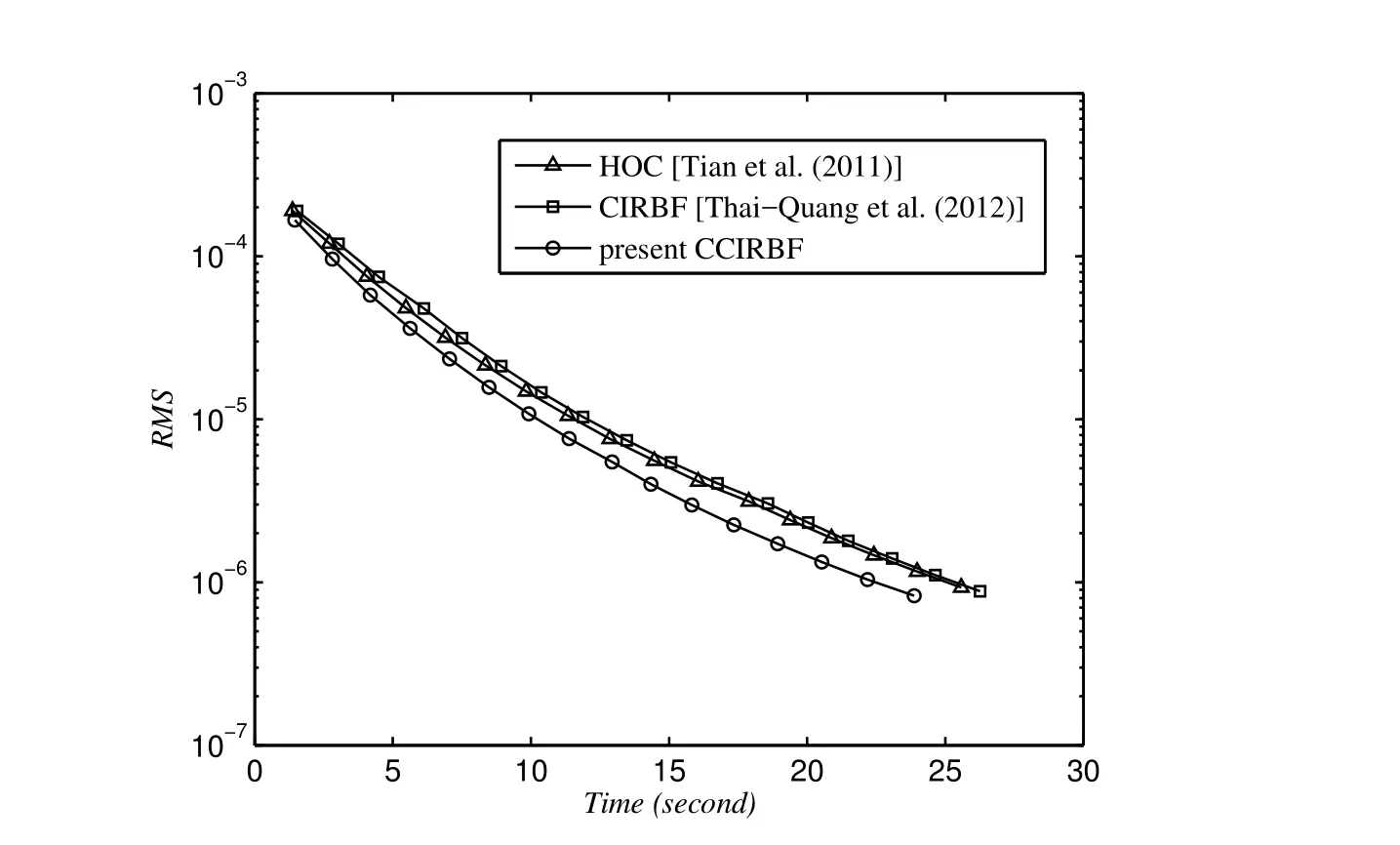
Figure 7:Heat equation,{11,13,...}:The computational cost to achieve the target accuracy of 10-6.The final grid is 43 for the HOC and CIRBF and 41 for the CCIRBF.

4.3 Burgers equation

With Burgers equation,the performance of the proposed scheme can be investigated for both convective and diffusive terms as

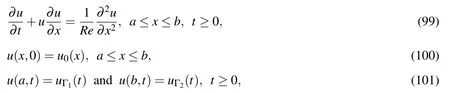
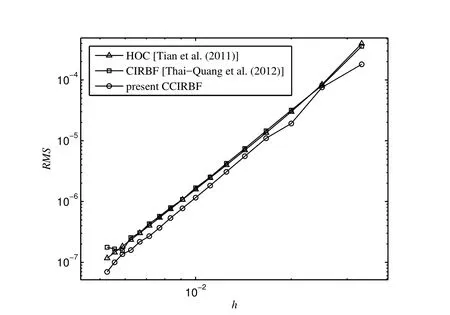
Figure 9:Burgers equation,{31,41,...,191},Re=100,Δt=10-6,t=0.0125:The effect of grid size h on the solution accuracy RMS.The solution converges as O(h4.29)for the HOC,O(h4.21)for the CIRBF,and O(h4.27)for the CCIRBF.

Figure 10:Burgers equation,{31,41,...,191},Re=100,Δt=10-6,t=0.0125:The effect of grid size h on the matrix condition number.It is noted that the curves for the HOC-ADI and CIRBF-ADI are indistinguishable.

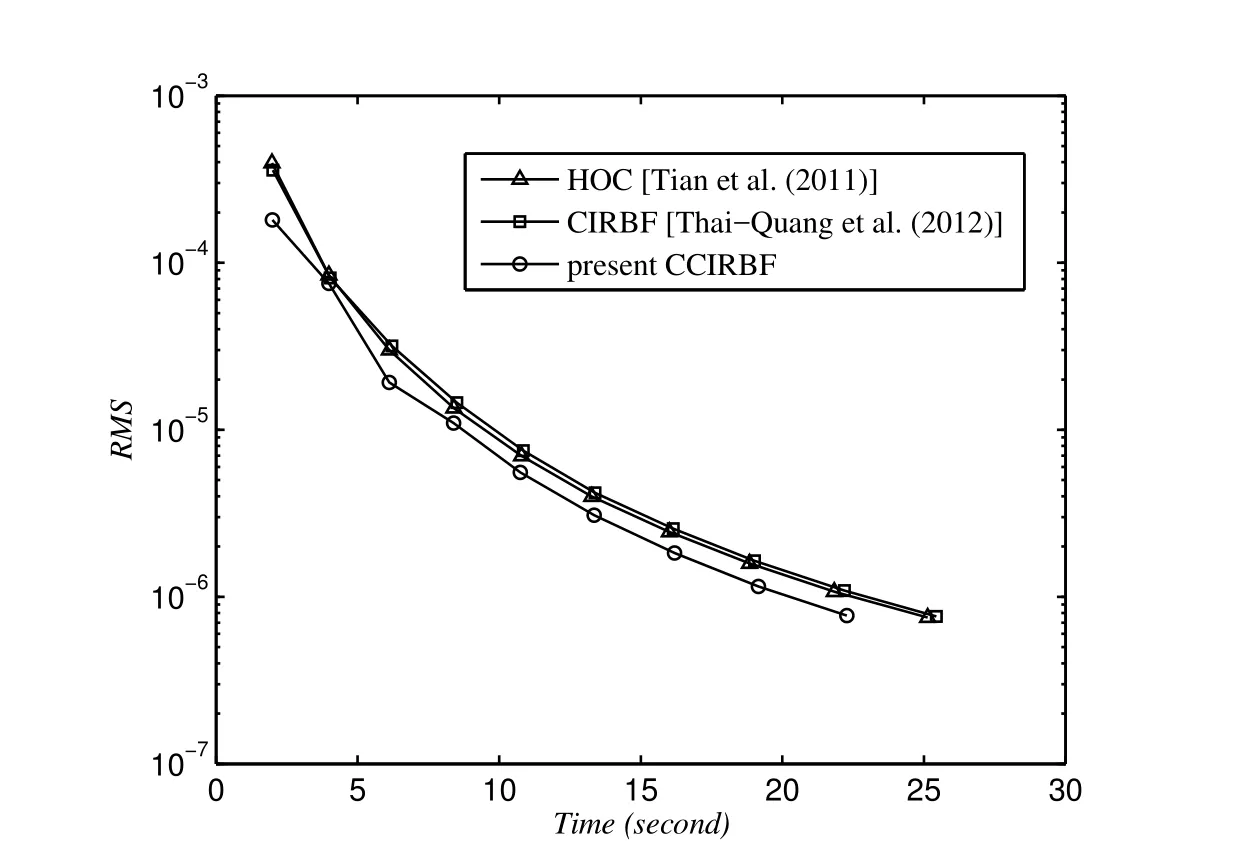
Figure 11:Burgers equation,{31,41,...}:The computational cost to achieve the target accuracy of 10-6.The final grid is 121 for the HOC and CIRBF and 111 for the CCIRBF.

Figure 12:Burgers equation,{31,71,101},Re=100,Δt=10-6,t=0.0125:The effect of the MQ width β on the solution accuracy RMS.

or

The problem is considered on a segment 0≤x≤1,t≥0 in the form[Hassanien,Salama,and Hosham(2005)]

where η =α0Re(x-µ0t-β0),α0=0.4,β0=0.125,µ0=0.6,and Re=100.The initial and boundary conditions can be derived from the analytic solution(104).The calculations are carried out on a set of uniform grids{31,41,...,191}.The time step Δt=10-6is chosen.The errors of the solution are calculated at the time t=0.0125.Figure 9 displays that the present scheme has lower errors than the HOC and CIRBF.At high grid densities,it can be also seen that the CCIRBF is more accurate and stable than the CIRBF.A similar trend of the matrix condition number for the three schemes is observed in Figure 10.

To study the computational efficiency of the CCIRBF,CIRBF and HOC schemes,we increase the number of grids as{31,41,...}until the solution accuracy achieves a target RMS level of 10-6.The time step Δt=10-6is chosen and the errors of the solution are calculated at the time t=0.0125.Figure 11 shows that the present scheme takes less time to reach the target accuracy than the CIRBF and HOC.It is noted that the final grid used to achieve the target accuracy is 121 for the HOC and CIRBF and 111 for the CCIRBF.

Figure 12 shows the effect of the MQ width on the solution accuracy,where the present scheme produces better accuracy than the CIRBF scheme over a wide range of β for three different grids{31,71,101}.

4.4 Steady convection-diffusion equation

Consider(76)with cx=cy=0.1,dx=dy=1 in a square Ω =[0,L]× [0,L]and subject to Dirichlet boundary condition.The analytic solution takes the form[Sheu,Kao,Chiu,and Lin(2011)]

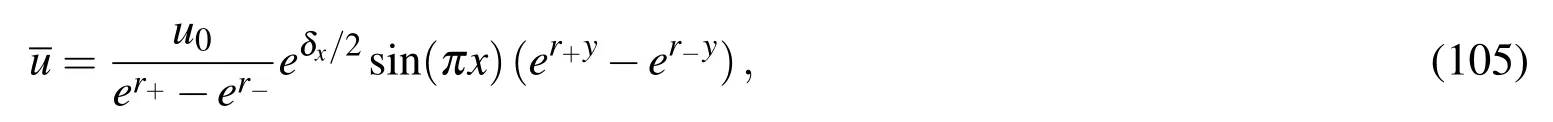
where u0=1,δx=cxL/dx,δy=cyL/dy,L=1,and

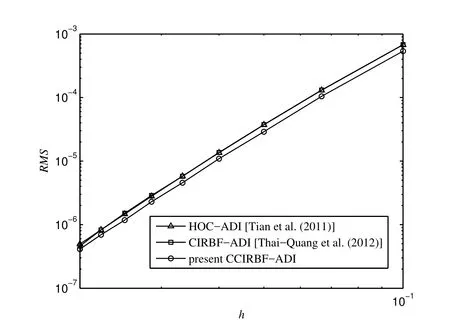
Figure 13:Steady convection-diffusion equation,{11×11,16×16,...,51×51}:The effect of grid size h on the solution accuracy RMS.The present solution is more accurate than those by HOC-ADI and CIRBF-ADI.

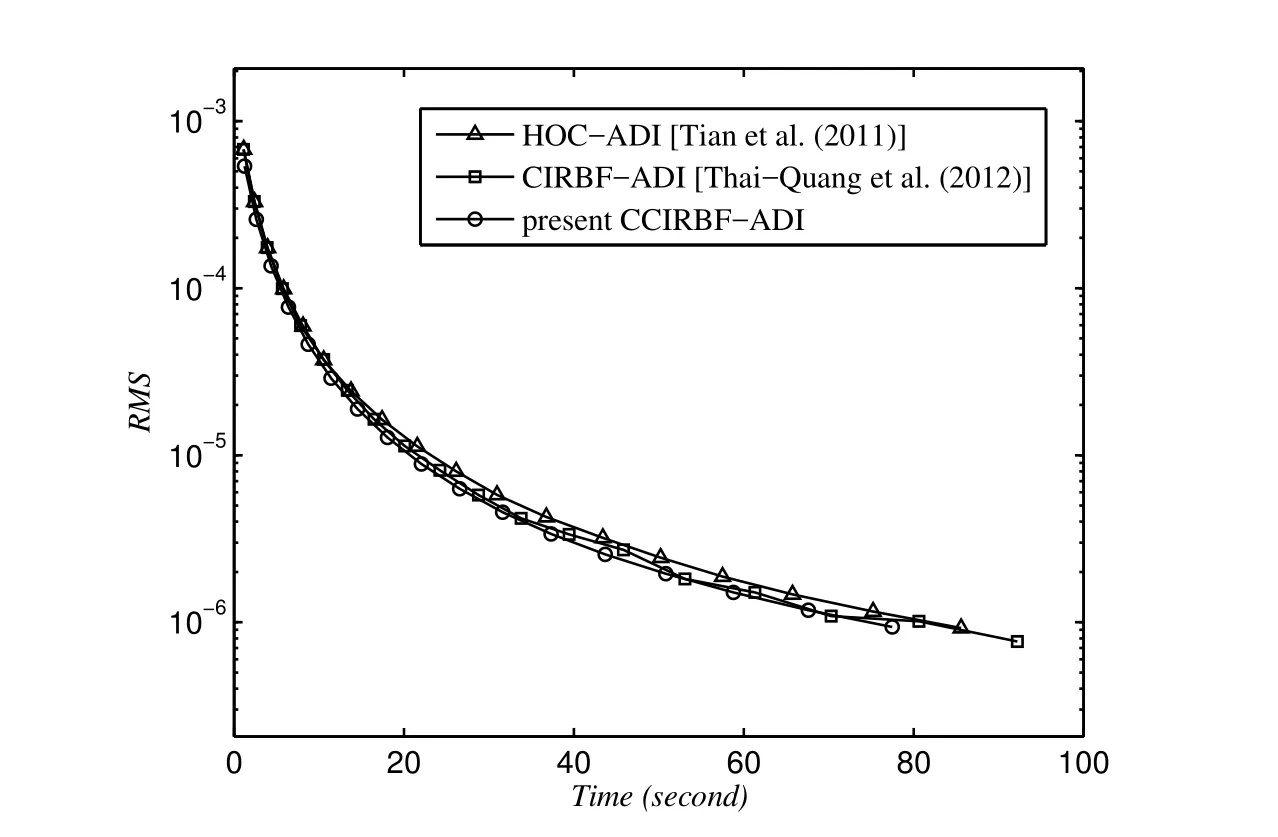
Figure 14:Steady convection-diffusion equation,{11×11,13×13,...}:The computational cost to achieve the target accuracy of 10-6.The final grid is 47×47 for the CIRBF-ADI,45×45 for the HOC-ADI and 43×43 for the CCIRBF-ADI.

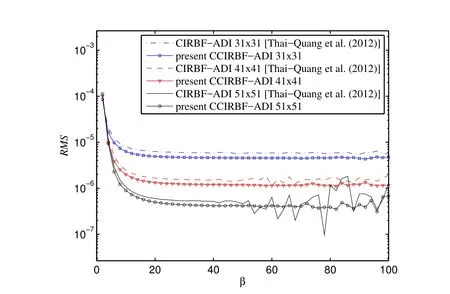
Figure 15:Steady convection-diffusion equation,{31×31,41×41,51×51}:The effect of the MQ width β on the solution accuracy RMS.

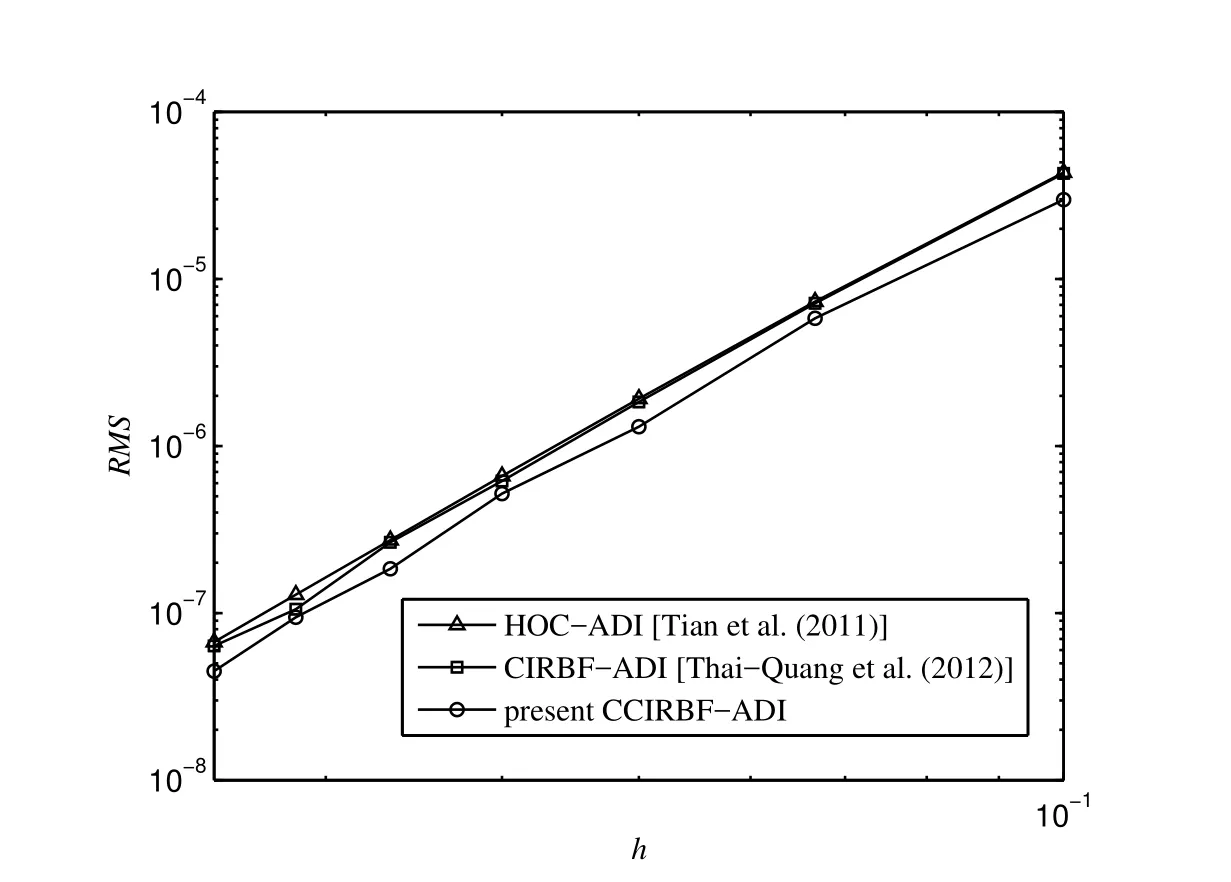
Figure 16:Unsteady diffusion equation,{11×11,16×16,...,41×41},Δt=10-5,t=0.0125:The effect of grid size h on the solution accuracy RMS.The present solution is more accurate than those by HOC-ADI and CIRBF-ADI.

The driving function fbis given by

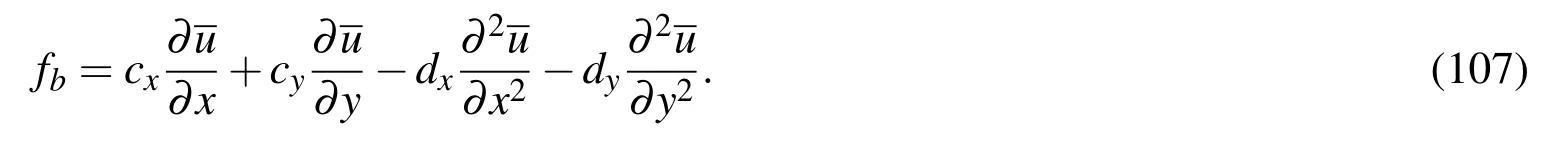
To solve the steady equation(76),we make use of the unsteady form(73)whereis considered as a pseudo time-derivative term to facilitate an iterative calculation.The steady equation(76)thus has the same form as the unsteady equation(73).When the difference of u between two successive time levels is small,i.e.less than a given tolerance(91),the obtained solution is the solution to(76).

In order to study the accuracy of the solution with grid re finement,we employ a set of uniform grids{11×11,16×16,...,51×51}and a time step of 0.0005.Figure 13 displays the present results are better than those of the HOC-ADI and CIRBF-ADI.To investigate the computational ef ficiency of the CCIRBF-ADI,CIRBF-ADI and HOC-ADI schemes,we let the number of grids increase as{11×11,13×13,...}until the solution accuracy achieves a target RMS level of 10-6.The time step is 0.0005.Figure 14 shows that the present scheme takes less time to reach the target accuracy than the CIRBF-ADI and HOC-ADI.It is noted that the final grid used to achieve the target accuracy is 47×47 for the CIRBF-ADI,45×45 for the HOC-ADI and 43×43 for the CCIRBF-ADI.

Figure 15 illustrates the solution accuracy versus the MQ width for three different grids{31×31,41×41,51×51}.It is observed that the CCIRBF-ADI is more accurate and stable than the CIRBF-ADI.

4.5 Unsteady diffusion equation

Consider a diffusion equation by setting the parameters in(73)as cx=cy=0,dx=dy=1 and fb=0.The analytic solution is taken here as[Tian and Ge(2007)]

The problem domain is chosen to be a unit square Ω =[0,1]× [0,1]and the initial and Dirichlet boundary conditions are derived from(108).

We employ a set of uniform grids{11×11,16×16,...,41×41}to study the accuracy of the solution with grid refinement.Results computed at t=0.0125 using Δt=10-5are displayed in Figure 16,showing that the CCIRBF-ADI gives lower errors than the HOC-ADI and CIRBF-ADI.

In order to investigate the computational efficiency of the CCIRBF-ADI,CIRBFADI and HOC-ADI schemes,we increase the number of grids as{11×11,13×13,...}until the solution accuracy achieves a target RMS level of 10-6.Results are also computed at t=0.0125 using Δt=10-5.Figure 17 shows that the present scheme reaches the target accuracy using less time than the CIRBF-ADI and HOCADI.It is noted that the final grid used to achieve the target accuracy is 25×25 for the HOC-ADI and CIRBF-ADI and 23×23 for the CCIRBF-ADI.

We employ a set of time steps Δt={0.05,0.025,0.0125,0.00625}to test the temporal accuracy.Results are computed at t=1.25 using a uniform grid of 81×81 are shown in Table 3.

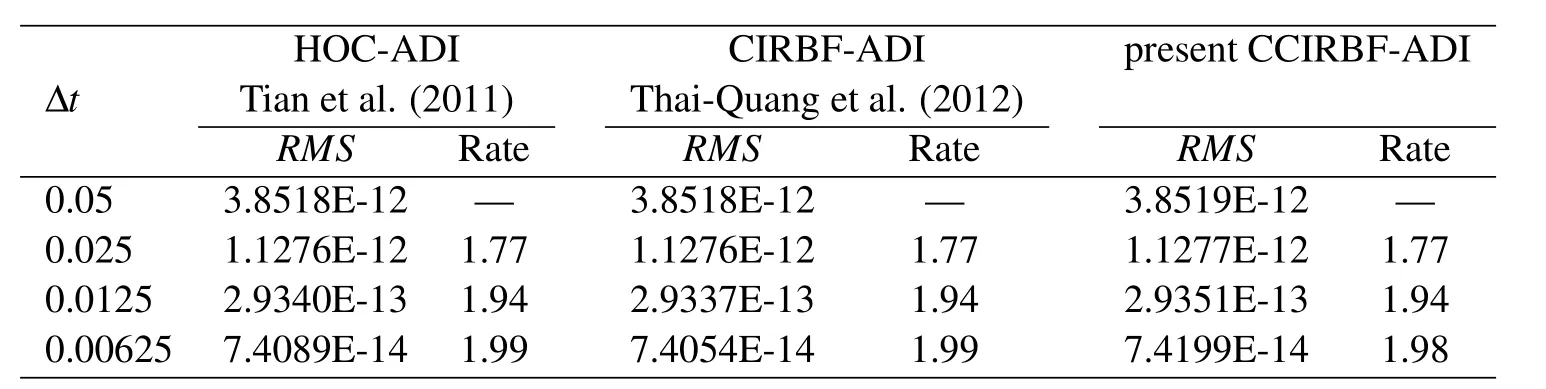
Table 3:Unsteady diffusion equation,t=1.25,grid 81×81:Solution accuracy of the three schemes against time step.

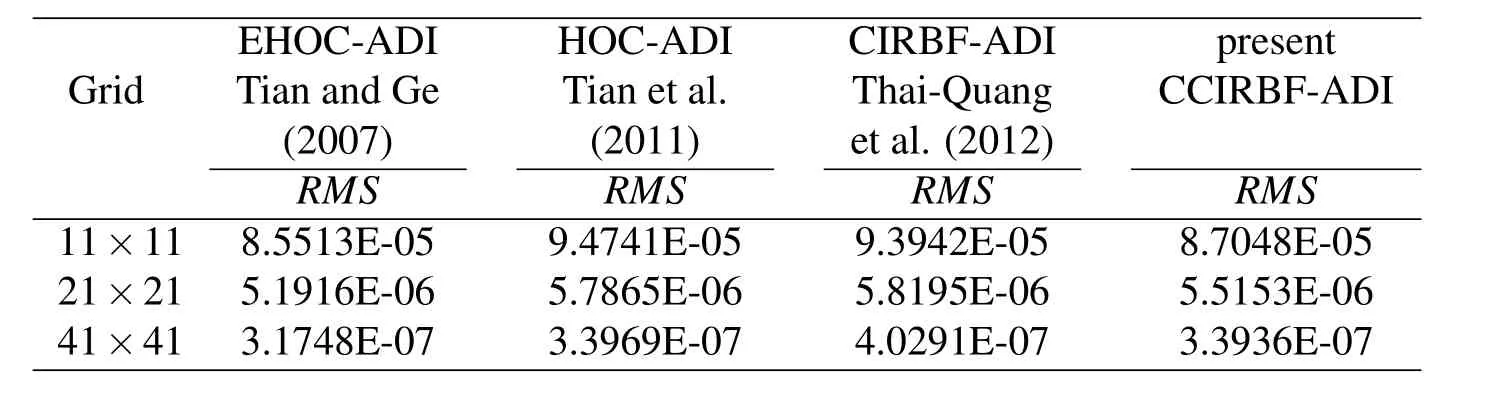
Table 4:Unsteady diffusion equation,t=0.125,Δt=h2:Effect of grid size on the solution accuracy RMS.

To facilitate a further comparison with the exponential high-order compact ADI scheme(EHOC-ADI)[Tian and Ge(2007)],we now choose Δt=h2andt=0.125.Table 4 indicates that the present CCIRBF-ADI scheme is more accurate than the HOC-ADI and CIRBF-ADI schemes and comparable with the EHOC-ADI scheme.The four schemes yield similar local rates of convergence of about 4.

Figure 18 plots the RMS error against time with Δt=10-4and t=0.125 using a grid of 21×21.The plot shows that the CCIRBF-ADI is more accurate than both HOC-ADI and CIRBF-ADI.

The effect of the MQ width on the solution accuracy for three different grids{21×21,31×31,41×41}is illustrated in Figure 19.

Figure 17:Unsteady diffusion equation,{11×11,13×13,...}:The computational cost to achieve the target accuracy of 10-6.The final grid is 25×25 for the HOCADI and CIRBF-ADI and 23×23 for the CCIRBF-ADI.

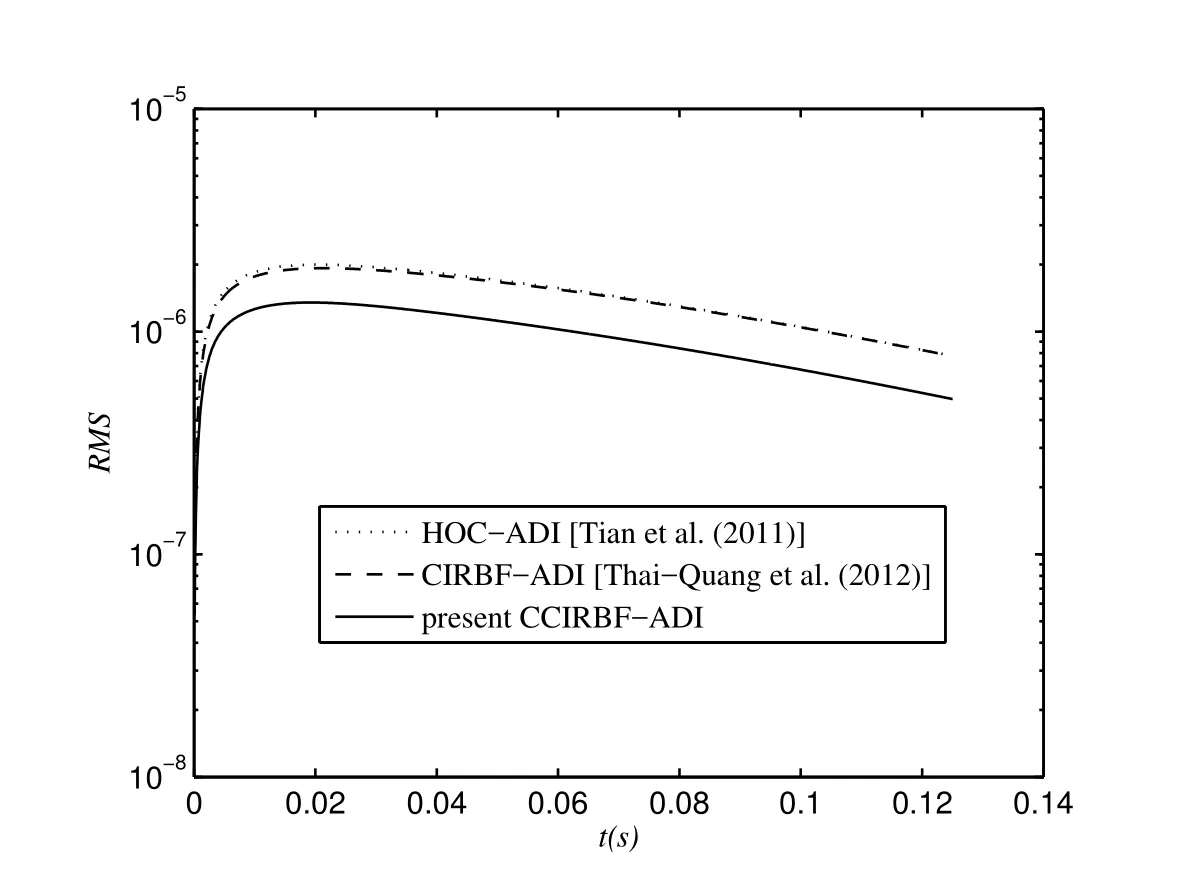
Figure 18:Unsteady diffusion equation,grid 21×21,Δt=10-4,t=0.125:The solution accuracy RMS against time.

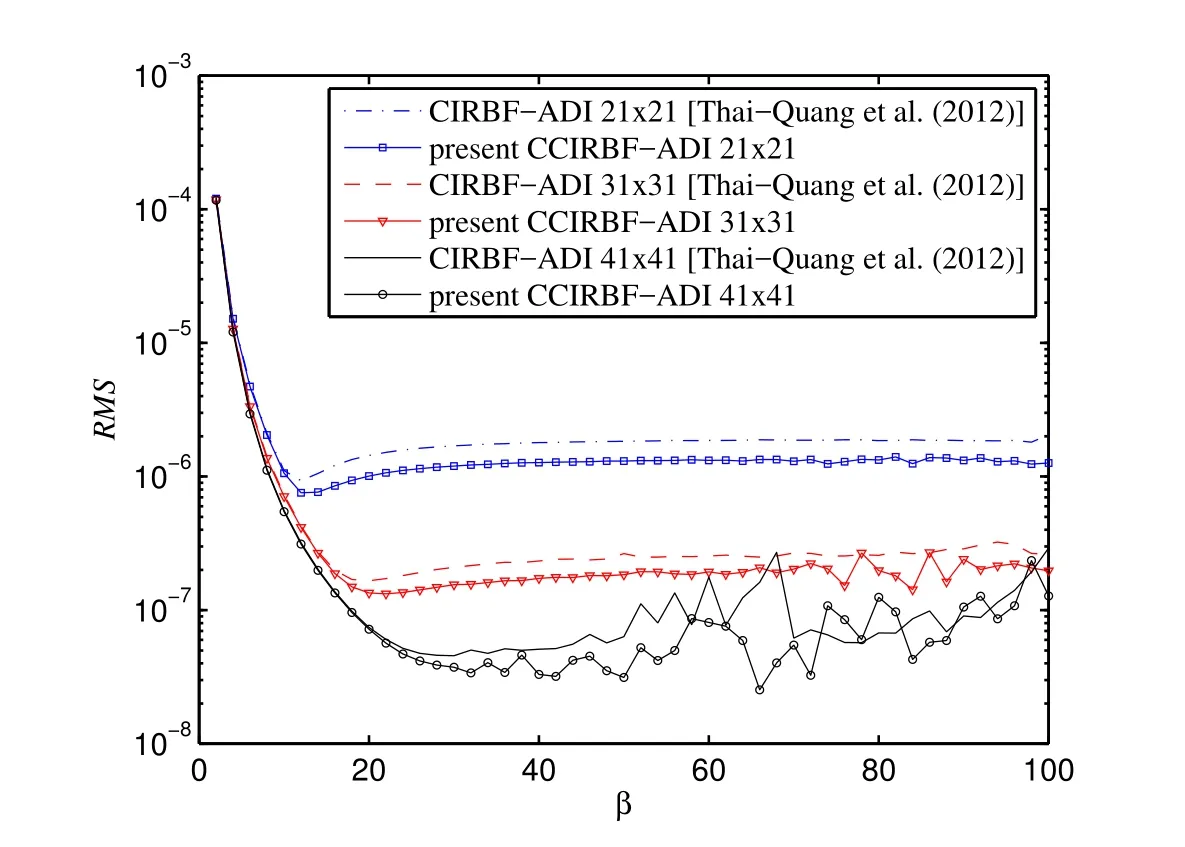
Figure 19:Unsteady diffusion equation,{21×21,31×31,41×41},Δt=10-4,t=0.125:The effect of the MQ width β on the solution accuracy RMS.

4.6 Unsteady convection-diffusion equation

Consider the unsteady convection-diffusion equation(73),where fb=0,in a square Ω=[0,2]×[0,2]with the following analytic solution[Noye and Tan(1989)]

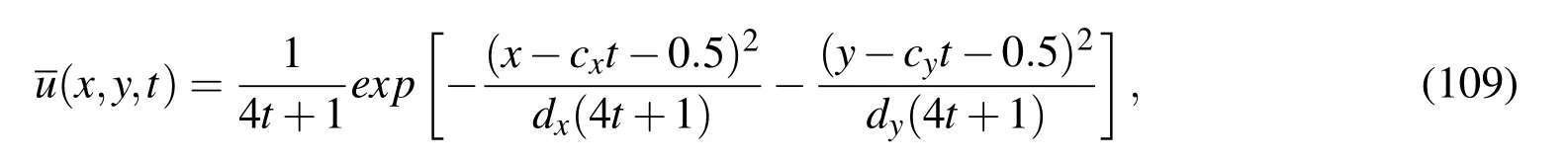
and subject to Dirichlet boundary conditions.From(109),one can derive the initial and boundary conditions.The problem parameters are chosen as cx=cy=0.8 and dx=dy=0.01.

To study the accuracy of the solution with grid refinement,we employ a set of uniform grids{31×31,41×41,...,81×81}.The solution is calculated at t=1.25 using Δt=10-4.Figure 20 describes that the proposed scheme has better performance than the HOC-ADI and CIRBF-ADI schemes.

To investigate the computational cost in achieving an accuracy of interest,we increase the grid{33×33,35×35,...}until the solution accuracy reaches the target accuracy which is chosen to be RMS=10-5.The solution is also calculated at t=1.25 using Δt=10-4.Figure 21 illustrates that for a given level of accuracy,the proposed scheme is more efficient than the HOC-ADI and CIRBF-ADI schemes.It is noted that the final grid used to achieve the target accuracy is 61×61 for the HOC-ADI and CIRBF-ADI and 45×45 for the CCIRBF-ADI.

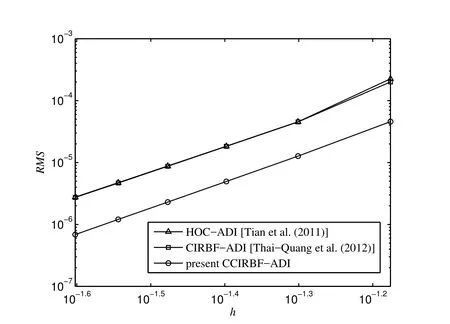
Figure 20:Unsteady convection-diffusion equation,cx=cy=0.8 and dx=dy=0.01,{31×31,41×41,...,81×81},Δt=10-4,t=1.25:The effect of grid size h on the solution accuracy RMS.The solution converges as O(h4.41)for the HOCADI,O(h4.32)for the CIRBF-ADI,and O(h4.27)for the CCIRBF-ADI.

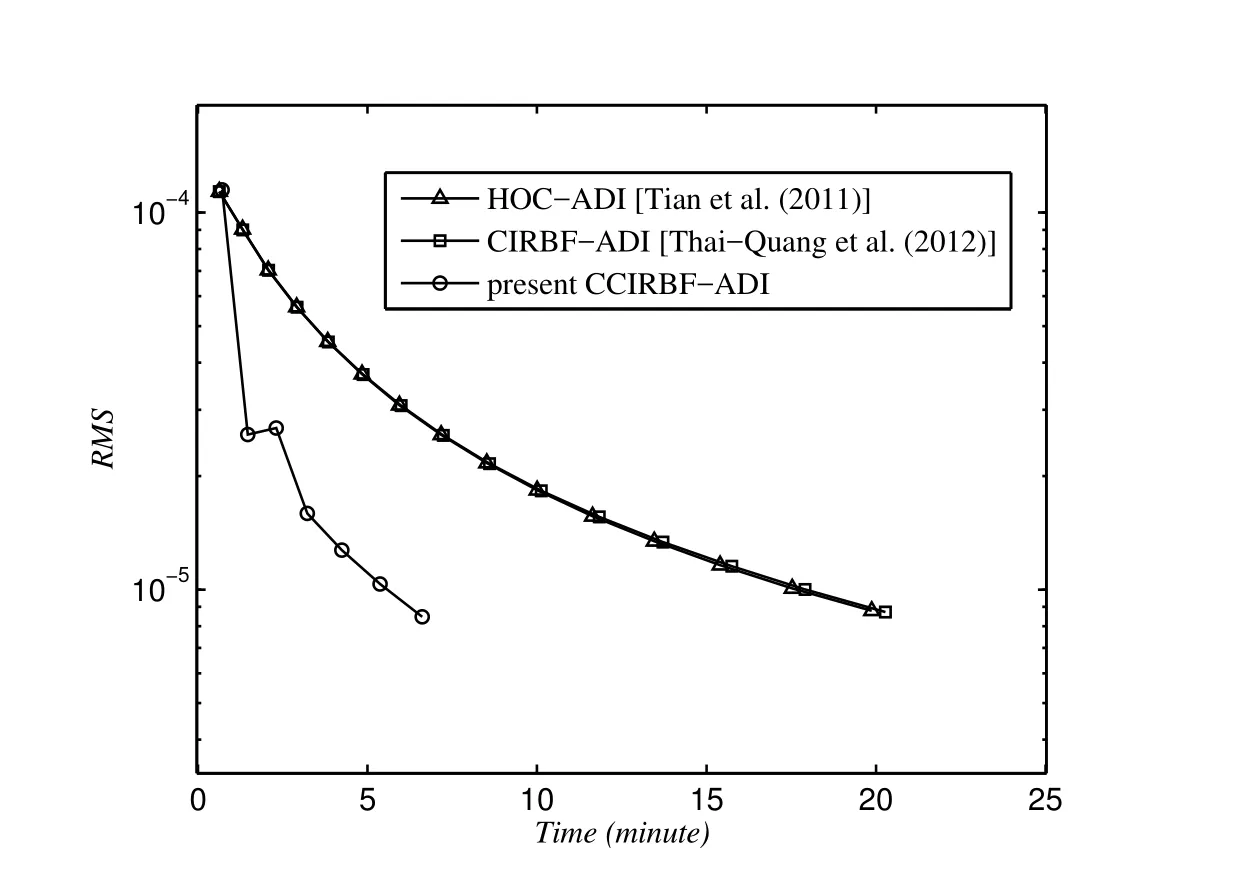
Figure 21:Unsteady convection-diffusion equation,{33×33,35×35,...}:The computational cost to achieve the target accuracy of 10-5.The final grid is 61×61 for the HOC-ADI and CIRBF-ADI and 45×45 for the CCIRBF-ADI.

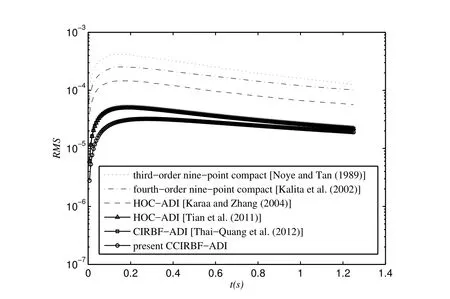
Figure 22:Unsteady convection-diffusion equation,cx=cy=0.8 and dx=dy=0.01,grid 81×81,Δt=0.00625,t=1.25:The solution accuracy RMS against time.It is noted that the curves for the HOC-ADI and CIRBF-ADI are indistinguishable.

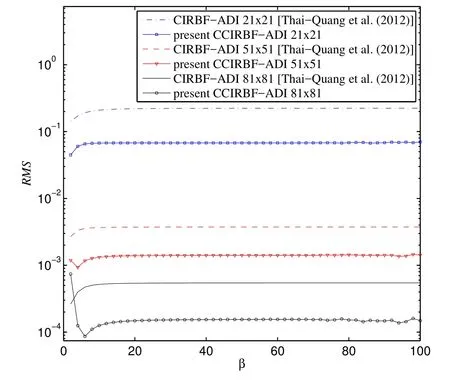
Figure 24:Unsteady convection-diffusion equation,case II,{21×21,51×51,81×81}:The effect of the MQ width β on the solution accuracy RMS.

Table 5 shows a comparison of L1,RMS and L∞errors between the present scheme and the third-order nine-point compact scheme[Noye and Tan(1989)],fourth-order nine-point compact scheme[Kalita,Dalal,and Dass(2002)],HOC-ADI scheme[Karaa and Zhang(2004)],exponential high-order compact ADI(EHOC-ADI)[Tian and Ge(2007)],high-order compact boundary value method(HOC-BVM)scheme[Dehghan and Mohebbi(2008)],HOC-ADI scheme[Tian,Liang,and Yu(2011)],and CIRBF-ADI[Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2012)].It can be seen that the present scheme yields the most accurate solution.Furthermore,Figure 22 plots the solution accuracy against time for these schemes(except EHOC-ADI,for which the data are not available).It illustrates that all of these curves have similar shapes and the present scheme produces smaller error for every time step.

Ma,Sun,Haake,Churchill,and Ho(2012)proposed a high-order hybrid Pad-ADI(HPD-ADI)method for the convection-dominated diffusion problem and examined the performance of the HPD-ADI scheme via this example,which is also considered in[Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2012)].For comparison purposes,we also consider two sets of parameters used in their articles

Case I:cx=cy=0.8,dx=dy=0.01,t=1.25,Δt=2.5E-4.

Case II:cx=cy=80,dx=dy=0.01,t=0.0125,Δt=2.5E-6.

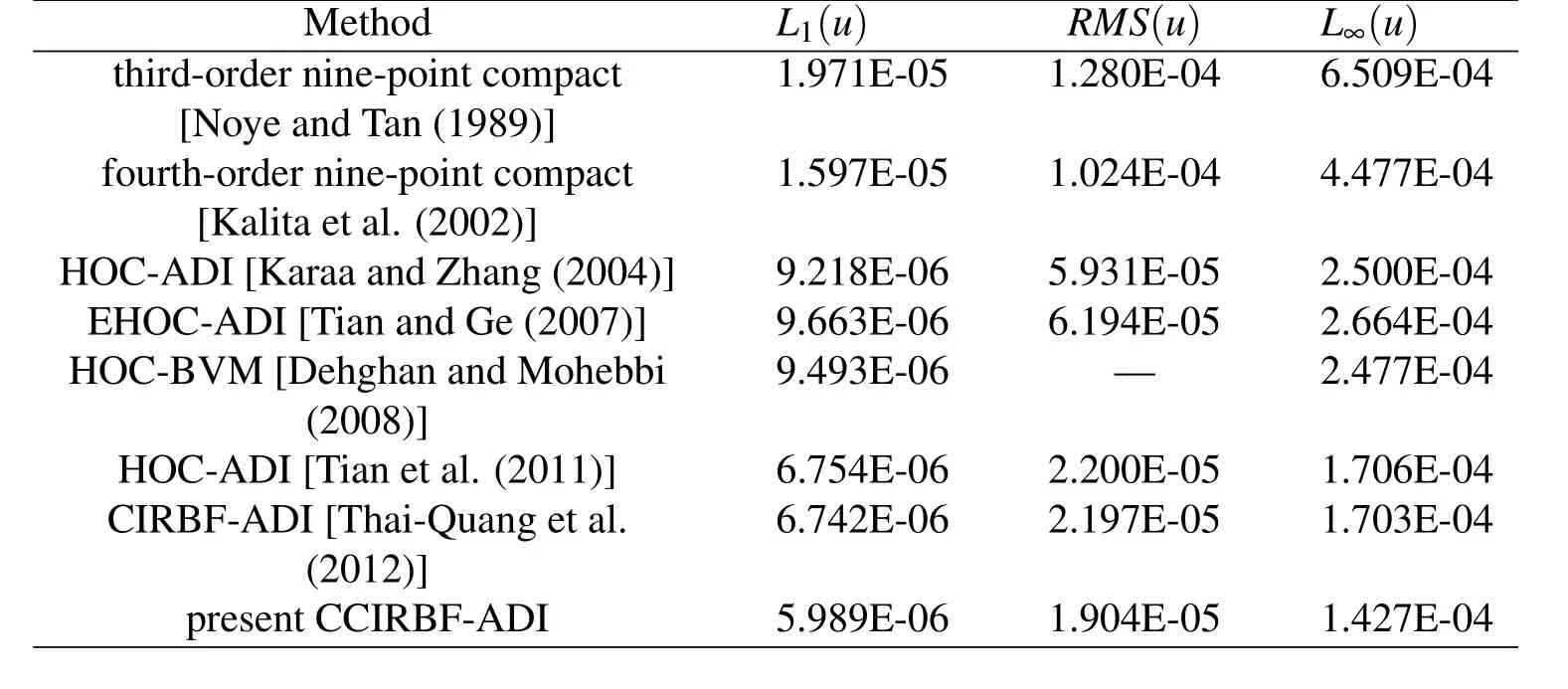
Table 5:Unsteady convection-diffusion equation,cx=cy=0.8 and dx=dy=0.01,grid 81×81,t=1.25,Δt=0.00625:Comparison of the solution accuracy between the present CCIRBF-ADI scheme and some others.

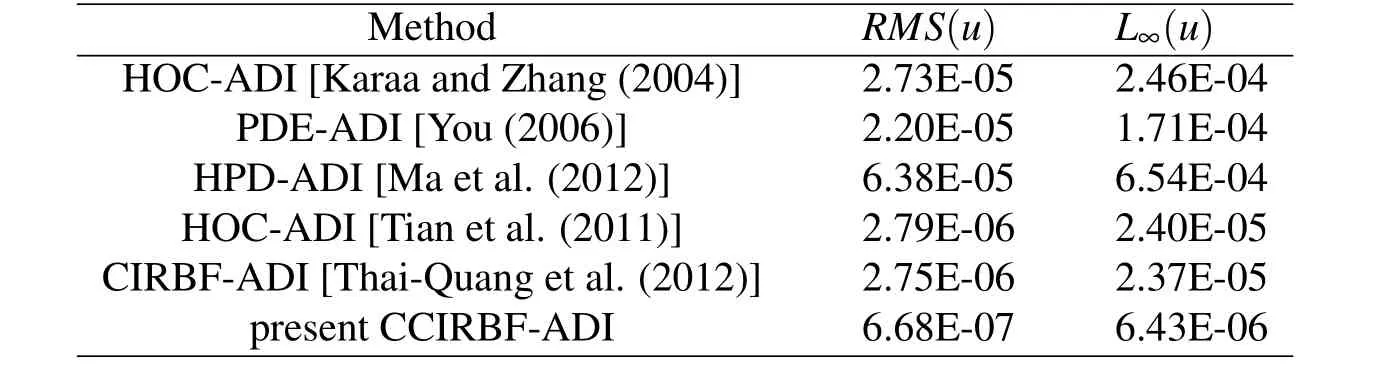
Table 6:Unsteady convection-diffusion equation,case I,grid 81×81:Comparison of the solution accuracy between the present CCIRBF-ADI scheme and some other techniques.

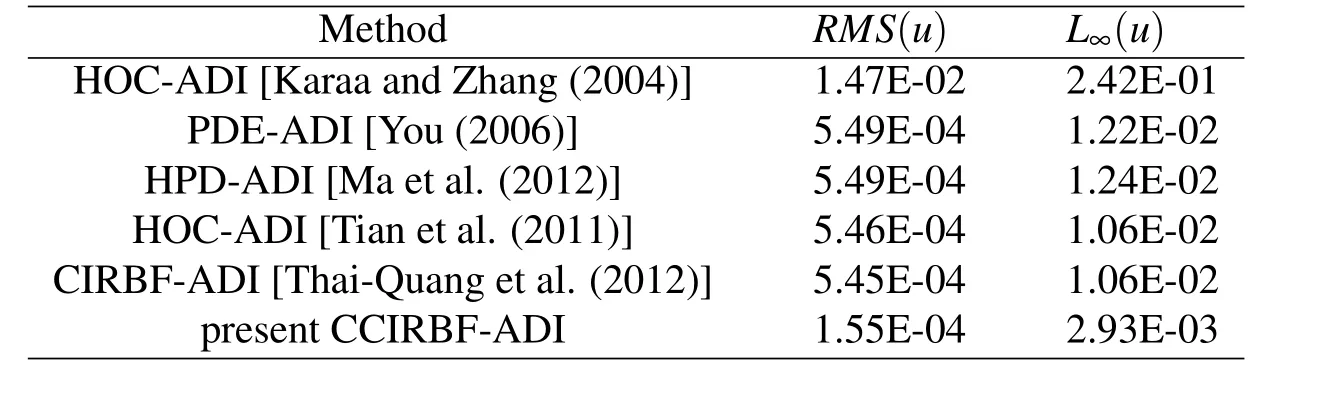
Table7:Unsteady convection-diffusion equation,caseII,grid81×81:Comparison of the solution accuracy between the present CCIRBF-ADI scheme and some other techniques.

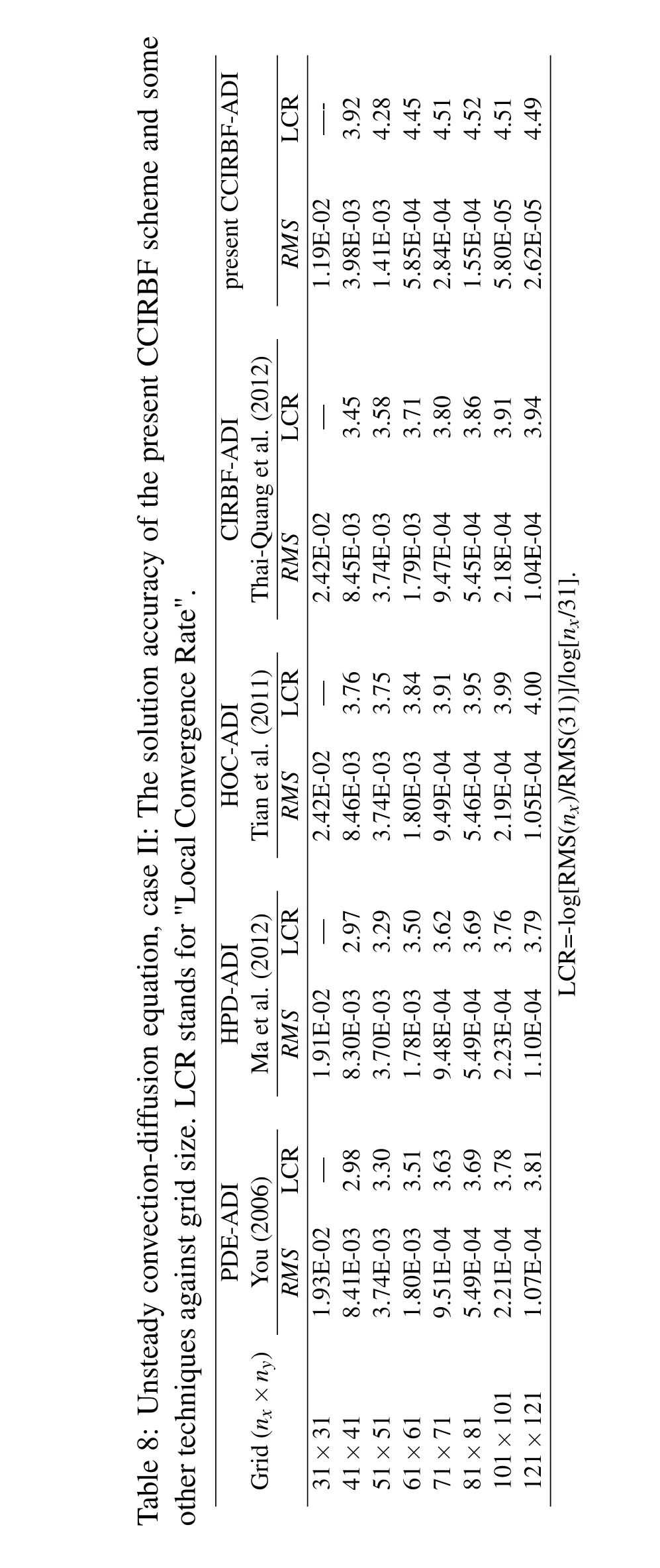
The corresponding Peclet number is thus Pe=2 for case I and Pe=200 for case II.Results concerning RMS and L∞errors are presented in Tables 6-8.In the case of low Pe,the present scheme is superior to the HPD-ADI and also other schemes(Table 6).In the case of high Pe(i.e.convection dominated),the CCIRBF-ADI yields the best performance:higher degrees of accuracy(Table 7)and higher rates of convergence(Table 8).

The effect of the MQ width on the solution accuracy is also plotted in Figure 23 for case I and in Figure 24 for case II.In both plots,it can be seen that the CCIRBFADI gives much more accurate results than the CIRBF-ADI.

5 Concluding remarks

A coupled compact integrated radial basis function(CCIRBF)scheme has been proposed in this paper.The proposed scheme is constructed over a three-point stencil,where nodal first and second derivative values of the field variable are both incorporated into the approximation by means of their identity equations.This leads to a significant improvement in accuracy and stability in comparison with the normal compact integrated radial basis functions(CIRBF).Numerical examples indicate that the results obtained by the present scheme are superior to those of the CIRBF,HOC and some other high-order schemes.Moreover,the enhanced convergence rate of the present scheme provides the present scheme with an ability to obtain prescribed accuracy using smaller amount of time compared with the CIRBF and HOC schemes.It can be stated that the CCIRBF scheme is a stable,efficient and promising highly accurate method for both derivative computation and second-order differential solutions.

Acknowledgement:The first author would like to thank USQ for an International Postgraduate Research Scholarship.This work was supported by the Australian Research Council.

Adam,Y.(1977):Highly accurate compact implicit methods and boundary conditions.Journal of Computational Physics,vol.24,pp.10-22.

Dehghan,M.;Mohebbi,A.(2008):High-order compact boundary value method for the solution of unsteady convection-diffusion problems. Mathematics and Computers in Simulation,vol.79,pp.683-699.

Elgohary,T.;Dong,L.;Junkins,J.;Atluri,S.(2014):A simple,fast,and accurate time-integrator for strongly nonlinear dynamical systems.CMES:Computer Modeling in Engineering and Sciences,vol.100,no.3,pp.249-275.

Elgohary,T.;Dong,L.;Junkins,J.;Atluri,S.(2014): Time domain inverse problems in nonlinear systems using collocation&radial basis functions.CMES:Computer Modeling in Engineering and Sciences,vol.100,no.1,pp.59-84.

Hassanien,I.A.;Salama,A.A.;Hosham,H.A.(2005): Fourth-order finite difference method for solving burgers equation.Applied Mathematics and Computation,vol.170,pp.781-800.

Hirsh,R.S.(1975):Higher order accurate difference solutions of fluid mechanics problems by a compact differencing technique.Journal of Computational Physics,vol.19,pp.90-109.

Hon,Y.;Sarler,B.;Dong,D.(2015): Local radial basis function collocation method for solving thermo-driven fluid- flow problems with free surface. Engineering Analysis with Boundary Elements.

Kalita,J.C.;Dalal,D.C.;Dass,A.K.(2002): A class of higher order compact schemes for the unsteady two-dimensional convection-diffusion equation with variable convection coef ficients.International Journal for Numerical Methods in Fluids,vol.38,pp.1111-1131.

Kansa,E.(1990a): Multiquadrics-a scattered data approximation scheme with applications to computational fluid-dynamics-i.surface approximations and partial derivative estimates.Computers and Mathematics with Applications,vol.19,no.8/9,pp.127-145.

Kansa,E.(1990b): Multiquadrics-a scattered data approximation scheme with applications to computational fluid-dynamics-ii.solutions to parabolic,hyperbolic and elliptic partial differential equations.Computers and Mathematics with Applications,vol.19,no.8/9,pp.147-161.

Karaa,S.;Zhang,J.(2004): High order adi method for solving unsteady convection-diffusion problems.Journal of Computational Physics,vol.198,pp.1-9.

Kosec,G.;Zaloznik,M.;Sarler,B.;Combeau,H.(2011): A meshless approach towards solution of macrosegregation phenomena.Computers,Materials,&Continua,vol.22,no.2,pp.169-195.

Kun,Z.;Yang,M.;Zhang,Y.(2012):A compact finite-difference scheme based on the projection method for natural-convection heat transfer. Numerical Heat Transfer,Part B:Fundamentals,vol.61,no.4,pp.259-278.

Lele,S.K.(1992): Compact finite difference schemes with spectral-like resolution.Journal of Computational Physics,vol.103,pp.16-42.

Li,M.;Tang,T.(2001): A compact fourth-order finite difference scheme for unsteady viscous incompressible flows.Journal of Scientific Computing,vol.16,pp.29-45.

Ma,Y.;Fu,D.;Kobayashi,T.;Taniguchi,N.(1999):A compact fourth-order finite difference scheme for the steady incompressible navier-stokes equations.International Journal for Numerical Methods in Fluids,vol.30,pp.509-521.

Ma,Y.;Sun,C.-P.;Haake,D.;Churchill,B.M.;Ho,C.-M.(2012):A highorder alternating direction implicit method for the unsteady convection-dominated diffusion problem.International Journal for Numerical Methods in Fluids,vol.70,no.6,pp.703-712.

Mahesh,K.(1998):A family of high order finite difference schemes with good spectral resolution.Journal of Computational Physics,vol.145,pp.332-358.

Mai-Duy,N.;Tanner,R.(2007):A collocation method based on one-dimensional rbf interpolation scheme for solving pdes. International Journal of Numerical Methods for Heat and Fluid Flow,vol.17,no.2,pp.165-186.

Mai-Duy,N.;Tran-Cong,T.(2001a): Numerical solution of differential equations using multiquadric radial basis function networks.Neural Networks,vol.14,pp.185-199.

Mai-Duy,N.;Tran-Cong,T.(2001b):Numerical solution of navier-stokes equations using multiquadric radial basis function networks.International Journal for Numerical Methods in Fluids,vol.37,pp.65-86.

Mai-Duy,N.;Tran-Cong,T.(2003):Approximation of function and its derivatives using radial basis function networks.Applied Mathematical Modelling,vol.27,pp.197-220.

Mai-Duy,N.;Tran-Cong,T.(2005):An efficient indirect rbfn-based method for numerical solution of pdes.Numerical Methods for Partial Differential Equations,vol.21,pp.770-790.

Mai-Duy,N.;Tran-Cong,T.(2011): Compact local integrated-rbf approximations for second-order elliptic differential problems. Journal of Computational Physics,vol.230,pp.4772-4794.

Mai-Duy,N.;Tran-Cong,T.(2013):A compact five-point stencil based on integrated rbfs for 2d second-order differential problems.Journal of Computational Physics,vol.235,pp.302-321.

Mramor,K.;Vertnik,R.;Sarler,B.(2013):Low and intermediate re solution of lid driven cavity problem by local radial basis function collocation method.CMCComputers,Materials and Continua,vol.1,pp.1-21.

Ngo-Cong,D.;Mai-Duy,N.;Karunasena,W.;Tran-Cong,T.(2012): Local moving least square-one-dimensional irbfn technique:Part ii-unsteady incompressible viscous flows.CMES:Computer Modeling in Engineering and Sciences,vol.83,no.3,pp.311-351.

Noye,B.J.;Tan,H.H.(1989): Finite difference methods for solving the twodimensional advection-diffusion equation. International Journal for Numerical Methods in Fluids,vol.9,pp.75-98.

Rubin,S.;Khosla,P.(1977):Polynomial interpolation methods for viscous flow calculations.Journal of Computational Physics,vol.24,pp.217-244.

Sellountos,E.;Polyzos,D.;Atluri,S.(2012): A new and simple meshless lbie-rbf numerical scheme in linear elasticity.CMES:Computer Modeling in Engineering and Sciences,vol.89,no.6,pp.511-549.

Sheu,T.W.H.;Kao,N.S.C.;Chiu,P.H.;Lin,C.S.(2011): Development of an upwinding scheme through the minimization of modi fied wavenumber error for the incompressible navier-stokes equations.Numerical Heat Transfer,Part B:Fundamentals,vol.60,no.3,pp.179-202.

Spotz,W.F.;Carey,G.F.(1995): High-order compact scheme for the steady stream-function vorticity equations.International Journal for Numerical Methods in Engineering,vol.38,pp.3497-3512.

Thai-Quang,N.;Mai-Duy,N.;C.-D.Tran;Tran-Cong,T.(2013): A direct forcing immersed boundary method employed with compact integrated rbf approximations for heat transfer and fluid flow problems.CMES:Computer Modeling in Engineering and Sciences,vol.96,no.1,pp.49-90.

Thai-Quang,N.;Mai-Duy,N.;Tran,C.-D.;Tran-Cong,T.(2012):High-order alternating direction implicit method based on compact integrated-rbf approximations for unsteady/steady convection-diffusion equations.CMES:Computer Modeling in Engineering and Sciences,vol.89,no.3,pp.189-220.

Tian,Z.;Ge,Y.(2007): A fourth-order compact adi method for solving twodimensional unsteady convection-diffusion problems.Journal of Computational and Applied Mathematics,vol.198,pp.268-286.

Tian,Z.;Liang,X.;Yu,P.(2011): A higher order compact finite difference algorithm for solving the incompressible navier stokes equations.International Journal for Numerical Methods in Engineering,vol.88,pp.511-532.

You,D.(2006):A high-order pade adi method for unsteady convection-diffusion equations.Journal of Computational Physics,vol.214,no.1,pp.1-11.

1Computational Engineering and Science Research Centre,Faculty of Health,Engineering and Sciences,The University of Southern Queensland,Toowoomba,Queensland 4350,Australia.