沪深股市VaR的实证分析

王起凡

摘  要：随着2014年我国股市行情转好，股票市场的波动也不断加剧，市场风险日渐凸显。在关注市场收益率的同时，如何度量股市的波动性及其风险控制愈显重要。本文以反映我国股市总体走势变化的上证综合指数和深圳成分指数作为研究对象，建立反映波动性的GARCH族模型，发现沪市具有反杠杆效应和较高的风险回报率，而深市具有杠杆效应和较低的风险回报率。在VaR的估计方面，在各置信水平下EGARCH（1，1）模型和GARCH（1，1）模型分别在拟合沪市和深市的市场风险上效果最好，且沪市相比与深市具有相对较低的市场风险。最后，本文对以上实证结果做出分析，并据此得出了对于投资者、监管层以及市场的经验与启示。

关键词：波动性GARCH族模型;在险价值VaR;最大可能损失率

一、沪深股市波动性的度量

（一）数据选取与处理。为对沪深股市波动性进行研究，本文以各交易日上证综合指数和深圳成分指数的收盘指数作为研究对象。本文所用的历史数据为2009年1月5日至2015年4月3日共1516个交易日数据。其中，记1516个交易日的上证综合指数序列为{ZZt}，深圳成分指数序列为{CZt}，其中第一个历史交易日即2009年1月5日的上证综指、深证成指分别为ZZ1、CZ1，最后一个历史交易日即2015年4月3日的上证综指、深证成指分别为ZZ1516、CZ1516。用{LNZZt}、{LNCZt}分别表示上证综指和深证成指的自然对数序列。对{ZZt}、{CZt}序列运用对数收益率公式Rt=Ln（Pt）-Ln（Pt-1），其中Pt代表以上两种收盘指数，t=1，2...，得到共1515个历史数据的指数对数收益率序列，其中上证综指对数收益率序列记为{R1}，深证成指对数收益率序列记为{R2}。选择自然对数收益率Rt的原因在于，自然对数收益率比普通收益率具有更优越的统计特性：（1）对日收益率取自然对数可适当降低其异方差性;（2）对数变换后乘法运算变为加法运算，而计算时间序列的和比计算时间序列的乘积更为简便。

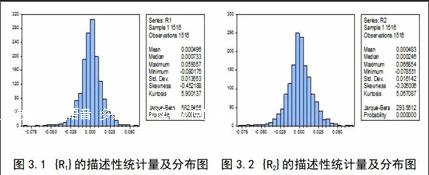
（二）上海与深圳股市收益率波动性的实证分析。（1）上海与深圳股市收益率的时间序列特征。首先对上证综指对数收益率序列{R1}和深证成指对数收益率序列{R2}进行描述性分析，其结果如下图3.1、3.2所示：

图3.1 {R1}的描述性统计量及分布图  图3.2 {R2}的描述性统计量及分布图

从图3.1的柱状图中不难看出，虽然该序列{R1}分布图总体形状与正态分布类似，但其尾部具有更多的值，即具有“厚尾”性质。该序列的的Jarque-Bera统计量为582.9456，相伴概率为0.000000。根据JB统计量与其P值，拒绝零假设，即该序列不服从正态分布，因此不能用该分布对其进行模拟。该分布的峰度峰度（Kurtosis）为5.900137，显著大于标准正态分布的峰度说明了该序列分布的“尖峰”性质。

从图3.2的柱状图中不难看出，虽然该序列{R2}分布图总体形状与正态分布类似，但其尾部具有更多的值，即具有“厚尾”性质。其次，该序列的Jarque-Bera统计量为293.5612，相伴概率为0.000000。根据JB统计量与其P值，拒绝零假设，该序列不服从正态分布，因此不能用该分布对其进行模拟。该分布的峰度（Kurtosis）为5.067087，显著大于标准正态分布的峰度说明了该分布的“尖峰”性质。同序列{R1}的柱状分布图与描述性统计量相比，序列{R2}总体情况和序列{R1}较为接近。

（2）平稳性检验。利用ADF检验法对序列{R1}和{R2}的平稳性进行检验，检验结果如下：

图3.3 {R1}的平稳性检验结果    图3.4 {R2}的平稳性检验结果

检验结果显示：{R1}和{R2}的ADF检验值其绝对值均显著大于各置信水平下临界值的绝对值，因此上证综指对数收益率序列{R1}与深圳综指对数收益率序列{R2}具有平稳性。

（3）自相关性检验。取最大滞后期为24，序列{R1}和{R2}自相关性检验结果如下：

图3.5 {R1}的自相关检验结果图        图3.6 {R2}的自相关检验结果图

检验结果显示：上证综指对数收益率序列{R1}和深圳综指对数收益率序列{R2}相关系数都不显著等于0，序列{R1}和

{R2}均不具有自相关性，因此将其GARCH模型的均值方程均设定成白噪声：Rt=μ+μt。

（4）ARCH效应检验。ARCH效应检验即检验均值方程残差项平方的自相关性，取最大滞后期为24，序列{R1}和{R2}的检验结果如下：

图3.7 {R1}的ARCH效应检验结果图   图3.8 {R2}的ARCH效应检验结果图

检验结果显示：序列{R1}和{R2}均值方程的残差项均具有自相关性，上证综指和深证成指对数收益率序列都存在ARCH效应。通过以上分析可知，序列{R1}和{R2}不服从正态分布，具有平稳性与ARCH效应且不具有自相关性，故可将条件方差引入条件均值模型中，建立GARCH族模型进行模拟，以研究上海股市和深圳股市的波动性。

（5）GARCH族模型的建立。在建立GARCH族模型前，首先需假设均值方程残差项的分布。因此在以下GARCH族模型建立时，需试算各分布，并选择最为合适的分布以得出最优

GARCH模型。经过反复试算我们发现，上证综指对数收益率与深证成指对数收益率的GARCH模型在GED分布下，其均值方程与方差方程的系数不仅统计显著，且最为显著（由于篇幅限制，试算结果未在正文中给出）。因此以下GARCH族模型都采用GED分布。同时为了模型的简洁性，在满足各系数显著的前提下，都利用GARCH（1，1）族模型拟合沪深股市波动性。

（1） GARCH模型。上证综指对数收益率序列的GARCH

（1，1）模型表达式：

（3.1）

深证成指对数收益率序列的GARCH（1，1）模型表达式：

（3.2）

对上证综指对数收益率序列{R1}和深证成指对数收益率序列{R2}的残差序列进行滞后一阶的ARCH-LM检验，结果如下：

图3.9 {R1} ARCH效应检验结果         图3.10 {R2}的ARCH效应检验结果

检验结果显示：{R1}和{R2}的nR2的伴随概率分别为0.2130和0.2350，均大于0.05的显著水平，因此上证综指和深证成指对数收益率序列不再具有ARCH效应，GARCH（1，1）模型可以消除上证综指和深证成指对数收益率残差序列的条件异方差。

根据上证综指和深证成指的GARCH（1，1）模型的表达式，上证综指与深证成指对数收益率的GARCH（1，1）模型的μ■■项与σ■■的系数都统计显著并且其之和接近且小于1，满足平稳条件，因此条件方差所受冲击是持续的，即上海市场与深圳市场的波动存在高持续性。当股市受到冲击而出现的异常波动在短期内很难消除，这也体现了我国股市具有较大的风险。

（2） GARCH-M模型。上证综指对数收益率序列的

GARCH-M（1，1）模型表达式：

（3.3）

深证成指对数收益率序列的GARCH-M（1，1）模型表达式：

（3.4）

对上证综指对数收益率序列{R1}和深证成指对数收益率序列{R2}的残差序列进行滞后一阶的ARCH-LM检验，结果如下：

图3.11 {R1}的ARCH效应检验结果图       3.12 {R2}的ARCH效应检验结果

检验结果显示：{R1}和{R2}的nR2的伴随概率为0.1950和

0.2285，大于0.05的显著水平，因此上证综指和深证成指对数收益率序列不再具有ARCH效应，GARCH-M（1，1）模型可以消除上证综指和深证成指对数收益率残差序列的条件异方差。

在均值方程中引入σ■■的原因是为了在解释金融资产收益率时引入随机误差项的条件方差来反映风险大小。因为高风险必然带来高收益，因此σ■■的系数必定为正数。上述两种指数对数收益序列的GARCH-M模型均值方程中，上证综指对数收益率序列中σ■■的系数等于2.013164，表明当上海市场预期风险增加1%时，其收益率将相应增加2.013164%。深证成指对数收益率序列的σ■■的系数为0.675317，表明当深圳市场预期风险增加1%时，其收益率将相应增加0.675317%。因此上海市场的风险回报更高。两指数的对数收益率序列的所有系数均统计显著，且μ■■项和σ■■的系数均统计显著且其之和接近但小于1，满足平稳条件。

（3）EGARCH模型。上证综指对数收益率序列的EGARCH

（1，1）模型表达式：

（3.7）

深证成指对数收益率序列的EGARCH（1，1）模型表达式：

（3.8）

对上证综指对数收益率序列{R1}和深证成指对数收益率序列{R2}的EGARCH（1，1）模型的回归结果进行滞后一阶的ARCH-LM检验，结果如下：

图3.13 {R1}的ARCH效应检验结果       图3.14 {R2}的ARCH效应检验结果

检验结果显示：{R1}和{R2}的nR2的伴随概率为0.2324和

0.2564，大于0.05的显著水平，因此上证综指和深证成指对数收益率的残差序列不再具有ARCH效应，EGARCH（1，1）模型可以消除上证综指和深证成指对数收益率残差序列的条件异方差。根据上证综指和深证成指的EGARCH（1，1）的模型表达式，上证综指对数收益率的EGARCH（1，1）模型非对称项系数大于0，说明上海市场具有反杠杆效应，即“利好消息”比等量“利空消息”可以产生更大冲击。而深证成指对数收益率的EGARCH

（1，1）模型非对称项系数小于0，说明深圳市场存在杠杆效应，即“利空消息”比等量“利好消息”能够产生更大冲击。特别地，上海市场出现利好消息时，上证综指对数收益率将受到0.089810+0.004303倍的冲击，出现利空消息时，会受到0.089810-0.004303倍的冲击;深圳市场出现利好消息时，深证成指对数收益率将受到0.107216-0.015612倍的冲击，出现利空消息时，会受到0.107216+0.015612倍的冲击。

二、基于GARCH族模型的VaR测算与分析

（一）上证综指与深证成指的VaR的计算。上证综指和深证成指GARCH-VaR的计算结果如下表3.1所示。上证综指与深证成指GARCH-VaR的计算结果表明：当置信水平上升时，不同GARCH模型得出的VaR值也上升，相应VaR的最大值、最小值、标准差也提高，这符合我们对于置信水平的一般认识。对不同GARCH模型计算出的VaR进行比较发现，不同

GARCH模型计算出的VaR差异较小。为了进一步地判断不同

GARCH模型计算出的VaR的可靠性，以及不同置信水平下

VaR的可靠性，我们需要对VaR进行回测检验。

表3.1  上证综指与深证成指GARCH-VaR的计算结果

（二）上证综指与深证成指VaR的失败率回测检验。通过上证综指和深证成指在不同GARCH模型以及置信水平下估计出的VaR值，利用失败率回测检验法对上证综指和深证成指

的GARCH-VaR进行准确性检验。上证综指与深证成指的

GARCH-VaR的回测检验结果如下表3.2所示。

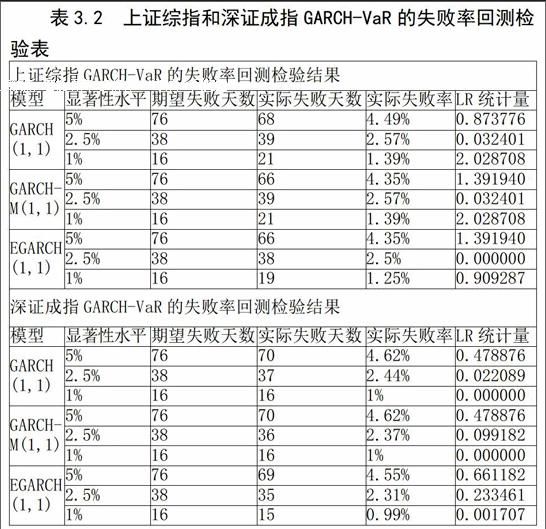
表3.2  上证综指和深证成指GARCH-VaR的失败率回测检验表

上证综指的GARCH-VaR的失败率回测检验表明：由于在95%、97.5%和99%置信水平下的x21-a（1）分别为3.841、5.024、6.635，四种GARCH模型在不同的置信水平下都通过了回测检验。且从LR统计量和实际失败率来看，95%置信水平下所有GARCH族模型都高估了实际风险，97.5%置信水平下除了EGARCH（1，1）模型外都低估了实际风险，99%置信水平下所有GARCH族模型都低估了实际风险。当置信水平一定时，所有GARCH模型中EGARCH（1，1）模型的LR统计量相对最低，因此我们认为EGARCH（1，1）模型具有最高的准确度，特别是当置信水平为97.5%时。

深证成指的GARCH-VaR的失败率回测检验表明：由于在95%、97.5%和99%置信水平下的x21-a分别为3.841、5.024、6.635，四种GARCH模型在不同的置信水平下都通过了回测检验。同上证综指的失败率回测检验结果相比，深证成指的失败率回测检验结果更优。从LR统计量和实际失败率来看，95%和97.5%置信水平下的所有GARCH族模型都高估了实际风险，

99%置信水平下的GARCH（1，1）和GARCH-M（1，1）模型都准确估计了VaR。当置信水平一定时，所有GARCH模型中GARCH（1，1）模型的LR统计量相对最低，因此我们认为GARCH（1，1）模型具有最高的准确度，特别是当置信水平为99%时，当然97.5%置信水平下的GARCH（1，1）也有较高准确度。

（三）上证综指和深证成指VaR的时间序列特征。根据以上GARCH-VaR回测检验结果，我们选择97.5%置信水平下的

EGARCH（1，1）模型度量的VaR结果作上证综指的时序图并选择97.5%置信水平下的GARCH（1，1）模型度量的VaR结果作深证成指的时序图，以研究它们的时间序列特征。

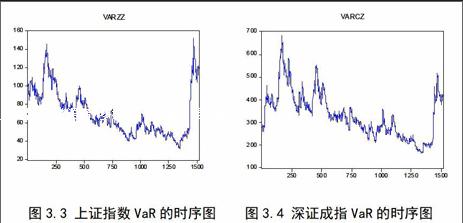
图3.3 上证指数VaR的时序图    图3.4 深证成指VaR的时序图

根据图3.3我们可以发现，上证综指的的VaR总体服从周期性波动。其中，深证成指的VaR从2009年5月27日到2009年9月4日迅速上升，在9月4日达到峰值，其后到2014年7月22日总体服从下降趋势，直到2014年7月22日达到最小。从2014年7月22日起到2015年4月3日，上证综指的VaR直线上升。上证指数在2009年5月27日到

2009年11月23日间与2014年11月21日到2015年3月12日间出现了极端波动，其波动幅度大于正常幅度。

根据图3.4我们可以发现，深证成指的的VaR总体服从周期性波动。其中，深证成指的VaR从2009年6月24日到2009年9月4日迅速上升，在9月4日达到峰值，其后到2014年7月8日总体服从下降趋势，直到2014年7月8日达到最小。从2014年7月9日起至2015年4月3日，深证成指的VaR迅猛上升。深证成指的GARCH-VaR与上证综指的GARCH-VaR的变化基本一致，即上海股市和深圳股市具有一定的联动性。 深证成指在2009年6月24日到2009年11月24日间与2014年10月28日到2015年3月16日间出现了极端波动，其波动幅度大于正常幅度。

（四）上证综指和深证成指最大可能损失率的时间序列特

征。由于上证综指和深证成指在相同时间时的指数值是不等的，为了比较上海股市和深圳股市的市场风险，我们需要将最大可能损失值VaR这一绝对数转化为相对数的概念，即前文所提到的最大可能损失率L。因此根据公式（2.10），和上文一样，我们通过上证综指的EGARCH（1，1）模型和深证成指的GARCH（1，1）模型得出在97.5%置信水平下的VaR，计算出最大可能损失率L，继而得到上证综指和深证成指最大可能损失率的时间序列图：

图3.5 上证综指和深圳成指最大可能损失率的时序图

根据图3.5我们可以发现，上证综指和深证成指最大可能损失率的时序图与其VaR的时序图较为接近，均具有一定的周期性，且两地股市变化趋势具有一致性。值得注意的是，和VaR的时序图中的结果接近，上证综指的最大可能损失率在2009年9月1日达到峰值，在2014年7月22日达到最低，而深证成指的最大可能损失率在2009年9月4日达到峰值，在2014年7月8日达到最低。除此之外，上证指数在2009年7月20日到2009年11月24日间与2014年10月28日到2015年4月3日间出现极端波动，其波动幅度大于正常幅度。而深圳成指在2009年7月27日到2009年11月24日间与2014年10月21日到2015年4月3日出现极端波动，其波动幅度大于正常幅度。

在样本期内深证成指的最大可能损失率基本大于上证综指的最大可能损失率，因此我们认为深圳股市的市场风险要大于上海股市的市场风险。至于在样本期内的前20天左右，上证综指的最大损失收益率要明显大于深证成指对数收益率最大损失率的原因，笔者认为是因为样本期过短而导致的偏差，并且GARCH族模型是条件方差及其滞后项的函数，因此在较短的样本期内这个偏差会较为显著。

三、实证结果分析与经验启示

（一）实证结果分析。得出以下结论：（1）上证综指和深证成指的对数收益率序列具有条件异方差，因此存在波动集聚性。上证综指和深证成指对数收益率的GARCH（1，1）和GARCH-M（1，1）模型的持续性参数都非常接近1，这也从实证角度证明了其波动集聚效应。换言之，上海股市和深圳股市由于冲击而产生的波动以较慢的速度逐渐递减。（2）上证综指对数收益率和深证成指对数收益率的GARCH-M模型体现了上海股市比深圳股市有更高的风险回报率。上证综指对数收益率和深证成指对数收益率EGARCH模型的常数项显著小于0，表明上海股市和深圳股市收益水平为负，风险较大。（3）上证综指和深证成指的VaR以及最大可能损失率序列具有一定的周期性，且两股市

VaR的变化趋势一定的一致性。通过对比上证综指和深证综指的最大可能损失率序列图，我们发现上海股市的市场风险要小于深圳股市的市场风险。并且，上证综指和深证成指的

GARCH-VaR以及最大可能损失率序列并不稳定，其分别在

2014年7月22日和7月8日达到最低，而后迅猛上升。这是因为从2014年下半年起，我国股市从“熊市”向“牛市”转变，大量热钱涌入证券市场，随着股民投资热度的飙升，股市热度过高形成的“泡沫”相应地提高了股市的系统性风险。（4）上证综指对数收益率序列波动存在显著的反杠杆效应，即“利好消息”比等量“利空消息”可以产生更大冲击，反映在模型中即上证综指对数收益率序列的EGARCH（1，1）的杠杆因子显著为正。深证成指对数收益率序列波动具有明显的杠杆效应，即“利空消息”比等量“利好消息”可以产生更大的冲击，反映在模型中即深证成指对数收益率序列的EGARCH（1，1）的杠杆因子显著为负。上海股市具有反杠杆效应的原因是：同深圳股市相比，上海股市具有相对较低的风险和较高的风险回报率，因此投资者在上海股市较易获利，在投资时具有相对积极的投资情绪，因此对待利空消息相对较为理性，而对待好消息却极易激进投资。在此环境下，我国股市的特殊性更易对样本期内上海股市呈现出的反杠杆产生促进作用：①我国股市禁止卖空，当股市由于利好消息开始呈现上升趋势时，看空的投资者由于卖空限制而只能退出市场，因此这些投资者的信息并没有被释放出来导致市场对于利好消息反应强烈而忽视利空消息②特别地，近年来我国市场逐渐进入牛市，投资者出于“政策性看涨”对利好消息十分敏感，而对利空消息选择性忽视，形成了“追涨杀跌”的投资方式。相对的，深圳股市出现杠杆效应的原因是：深圳股市具有相对较高的风险和相对较低的风险回报率，因此投资者在深圳股市较难获利，所以投资者的投资情绪极度敏感，对待利空消息极易过度产生反应。并且，一般情况下，由于利空消息导致的股价下降会使得个股上市公司的债务权益比提高，继而公司财务风险也提高，这也促使了股价的进一步波动。在此环境下，我国股市投资者的特点也更以在高风险低回报的深圳股市中，对其杠杆效应的形成发挥作用：我国股市以散户为主，而散户大多为风险厌恶型，因此其对利空消息较易产生过度反应。当股市大盘出现合理的波动性的下跌时，投资者极易将其以为是新一轮“熊市”的信号进而大量抛售所持股票，进而导致抛压并产生“羊群效应”。而当大盘上升时，投资者由于曾经大盘暴跌而产生的心理阴影，习惯性地放弃继续持股等待进一步地上升，而是基于眼前利益稍有获利便了结持仓，股民的这一行为也压制了股价进一步的上扬趋势。（5）在利用GARCH模型估计VaR时，不同GARCH模型得出的VaR随置信水平的上升而上升，其最大值、最小值、标准差也相应上升。随着置信水平的提高，上证综指与深证成指的GARCH-VaR的实际失败率相应减小。在日常投资中，投资者还需结合实际情况调整置信水平，因为过低的置信水平会导致风险低估，继而带来损失;但过高的置信水平使投资者投入过度的风险准备金，过低的投资不仅降低了投资灵活性和流动性，也提高了投资成本。

所有GARCH族模型得出的VaR在不同置信水平中都通过了失败率回测检验，说明GARCH模型在估计VaR具备较高的精度。在不同GARCH模型估计上证综指的VaR中，

EGARCH（1，1）模型，特别是97.5%置信水平下的EGARCH（1，1）模型估计VaR的精度最高。而在不同GARCH模型估计深圳成指的VaR中，GARCH（1，1）模型，特别是99%置信水平下的GARCH（1，1）模型估计VaR的精度最高。

（二）经验启示。（1）投资者角度：把握沪深股市波动性规律，掌握科学的投资理念和投资方法。目前我国投资者的投资理念和投资方法较不成熟，散户的投资行为具有盲目性，常常“追涨杀跌”，对各类利好利空消息作出过度反应，这不仅加大了股市的震荡，也引起了沪深股市截然不同的杠杆性。事实上，通过前文的实证分析不难发现，股市波动性和风险具有一定的规律性。并且，GARCH族模型在估计和预测风险（在险价值）上具有显著的可靠性。因此，科学的投资方法和投资理念是可以帮助投资者获利的，而且这也会促进股市的平稳运行和良性发展，股市的平稳与健康也会从侧面降低市场风险，减少股市的不确定性，进而帮助投资者获利。（2）监管层角度：建立健全股市监管体系，促进股市健康稳定运行。虽然我国沪深股市的波动具有规律性，但我国沪深目前仍是一个“政策市”，其波动受政策面影响很大，因此极易产生极端波动，正如前文所说的

VaR和最大可能损失率在两个阶段出现极端波动。因此为了保证股市的稳定，监管层需保证政策的稳定性，以增强对市场风险的可控性。除此之外，监管层还需不断加强信息披露制度，减少股市的信息不对称以减少投资者投资行为的盲目性，使投资者可以全面合理地面对和解读各种利好与利空信息。并且，全面的监管体系也可以最大限制地抑制市场操纵行为和各类违规行为，为投资者建立一个公平、公正、稳定的投资环境，以增强投资者对股市的信心，增加投资者在投资中的参与度。（3）市场角度：完善市场标准，促进股市功能有效发挥。目前中国股市的市场标准很难让投资进行“价值投资”，使得大部分投资者进行投机行为。各类内幕交易事件与可疑交易使投资者将投资研究重心放在对消息的把握上，较少关注上市公司的基本面和内在价值。除此之外，股市的高溢价率使得投资者“打新”倾向严重，退市制度的不合理降低了股市的整体质量。前文结论中所描述的深市同沪市相比高风险低回报的原因，也是在于两市在股票类型以及股市质量的不同等多方面因素所导致的。因此，为了规范股市发展，使得股市真正实现企业融通资本、投资者投资获利的功能，股市的市场标准，特别是入市与退市制度还需进一步完善。

参考文献：

[1] 何敏园. 基于GARCH族模型的我国股市的波动性及联动性实证研究[D].中南大学，2010.

[2] 成城. 基于GARCH模型的上证指数波动率特征分析[D].山东大学，2014.