Kernel-Based Local Meshless Method for Solving Multi-Dimensional Wave Equations in Irregular Domain

Marjan Uddin,Hazrat Ali and Amjad Ali

Kernel-Based Local Meshless Method for Solving Multi-Dimensional Wave Equations in Irregular Domain

Marjan Uddin1,2,Hazrat Ali1and Amjad Ali1

This work explores the application of kernel based local meshless method for solving multi-dimensional wave equations in irregular domain.The method is tested for various types of boundary conditions in irregular shaped domain.The method is capable of solving multi-dimension large scaled problems in complex shaped domain.

Kernel functions,local meshless scheme,wave equation,complex shaped domain.

1 Introduction

The construction of robust and efficient numerical methods for solving large-scale wave problems in computational physics is an important and challenging research topic.The wave equation govern many physical problems such as the stress wave in an elastic solid,water wave propagation in water bodies,and sound wave propagation in a medium.The kernel-based numerical methods introduced in Hardy(1971)for scattered data fitting problems.It was shown in Micchelli(1984)that the system matrix for the MQ kernel is invertible.The kernels(RBFs)was first used for solving partial differential equations in the year 1990[Kansa(1990a,b)].In this original work the fluid mechanics problems were solved by approximating the derivatives by the derivative of MQ kernel functions directly.The convergence theory of kernel based approach was proved in Schaback(2007).During the past three decades a large number of robust kernel-based approximation methods have been developed[Atluri and Zhu(1998);Buhmann(2003);Wendland(2004);Fasshauer and Zhang(2007);Voller,Vertnik,and Šarler(2006);Sarra and Kansa(2009);Beatson,Davydov,and Levesley(2010);Georgoulis,Levesley,and Subhan(2013);Levesley and Sun(2005);Chen,Fu,and Chen(2014)],These methods have effectively used for solving many engineering and science problems[Elgohary,Dong,Junkins,and Atluri(2014);Dong,Alotaibi,Mohiuddine,and Atluri(2014);Sladek,Stanak,Han,Sladek,and Atluri(2013);Shibahara and Atluri(2011);Šarler(2005);Yao,Šarler,and Chen(2011);Yao,Sarler,et al.(2010);Fu,Chen,and Gu(2014);Lin,Chen,Chen,and Jiang(2013);Haq,Uddin,and Islam(2009);Uddin(2013);Uddin and Haq(2013)].The main advantage of using the kernels(RBFs)for the solution of PDEs is its simplicity,applicability to various PDEs,and effectiveness in dealing with multi-dimensional problems and complicated domains.In most global kernelbased methods the differentiation matrices are unsymmetric as well as dense.Due to the high resolution for large amount of data points it becomes difficult to solve the problem with global kernel based method.Many robust numerical approximation methods have been developed to overcome this difficulty some of them are the transforms based methods and the multipole approaches[Greengard and Strain(1991);Cherrie,Beatson,and Newsam(2002);Gumerov and Duraiswami(2007)],the domain decomposition methods[Beatson,Light,and Billings(2001);Kansa and Hon(2000);Li and Hon(2004)],the partition of unity methods[Wendland(2002)],the greedy algorithms[Schaback and Wendland(2000);Hon,Schaback,and Zhou(2003);Ling and Schaback(2008)],the multilevel methods[Fasshauer(1999);Fasshauer and McCourt(2012)],and the use of locally supported kernel functions[Wendland(1995);Floater and Iske(1996)].An other alternative approach to overcome this difficulty was developed by Tolstykh[Tolstykh(2000)],here local kernel interpolants in small domains centered around each node is used to form differentiation weights.This idea has been used to construct various types of local kernel based approximate methods and has been applied successfully to a wide range of problems.These include convection diffusion[Chandhini and Sanyasiraju(2007);Stevens,Power,Lees,and Morvan(2009);Šarler and Vertnik(2006);Sarra(2012)],incompressible Navier-Stokes[Chinchapatnam,Djidjeli,Nair,and Tan(2009);Shan,Shu,and Lu(2008);Shu,Ding,and Yeo(2003)],elliptic equations[Tolstykh and Shirobokov(2003);Wright and Fornberg(2006)]and[Wong,Hon,Li,Chung,and Kansa(1999);Xiao and McCarthy(2003);Brown,Ling,Kansa,and Levesley(2005)].In the present work we used the same idea to construct local kernel based numerical scheme for solving multi-dimensional wave equations in irregular domain.

2 Local meshless numerical scheme for time dependent PDEs

In this section,we describe a local RBF approximation method for

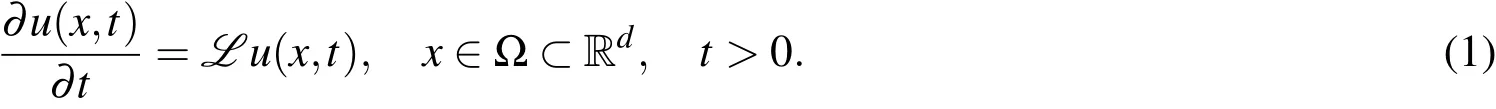
2.1 Spatial approximation

In multivariate scattered data interpolation,we always need to recover an unknown functionu:Rd→R from a given set ofNfunction values{u(x1),...,u(xN)}⊂R.Where the scattered centersx1,...,xN∈ Ω and Ω ⊂ Rdis arbitrary shaped domain and the centers can be chosen any where in the domain.In the local RBF approximation method,at each centerxi∈Ω,the local interpolant takes the form

where λi=[λ1,...,λn]is a vector of expansion coefficients,‖xi−xj‖,denotes the Euclidean distance between two centersxiandxj,φ(r)is a kernel function defined forr≥0 and Ωi⊂Ω is a local domain corresponding to each nodexiand containsnnearest centers around the centerxi.TheNnumber ofn×nlinear systems in matrix form are given by

wheretheentriesof thematrix Aiarethematrix Aiis called the interpolation matrix,and each system has to be solved for the expansion coefficients.In order to approximate the linear differential operator Lu(x,t),we have

The expression in(4)may be given as a dot product of two vectors,

where λiis then×1 vector of expansion coefficients,and viis 1×nvector with entries

To eliminate the expansion coefficients,we have from equation(3)

we substitute the values of λifrom(7)in(5)to get,

where,

is the weight corresponding to centerxi.Hence for all centers locations,we have

where W isN×Nsparse differentiation matrix,each row of the matrix W containsnnon-zeros elements andN−nzeros elements,wherenis the number of nodes in each local domain Ωi.

2.2 Temporal approximation

After spatial local RBF approximation,we obtained the following system of ODEs

In our caseF(u)=Wu.To discretize in time we can use any ODE solver like ode113,ode45 from Matlab.The starting vector will be the initial solutionu0.ode45 is based on an explicit Runge-Kutta(4,5)formula,the Dormand-Prince pair[Dormand and Prince(1980)].It is a one-step solver for computingu(tn),and it needs only the solution at the immediately preceding time point,u(tn−1).In general,ode45 is the best function to apply as a first try for most problems.ode113 is a variable order Adams-Bashforth-Moulton PECE solver[Shampine and Gordon(1975)].It may be more efficient than ode45 for stringent tolerances and when the ODE file function is particularly expensive to evaluate.ode113 is a multistep solver;it normally requires the solution at several preceding time points to compute thecurrentsolution.A good ODE solver will automatically selectareasonabletime step δtand detect stiffness of the ODE system.For this ODE computation we have used a fourth-order Runge-Kutta method and selected the time step δtmanually.

2.3 Stability of the local meshless numerical scheme

In the present local meshless method of lines our numerical scheme is given by here the time-dependent PDE is transformed into a system of ODEs in time.The method of lines refers to the idea of solving the coupled system of ODEs by a fi nite difference method in t(e.g Runge-Kutta,etc.).The numerical stability of the method of lines is investigated by a rule of rhumb.The method of lines is stable if the eigenvalues of the(linearized)spatial discretization operator,scaled byδt,lie in the stability region of the time-discretization operator[Trefethen(2000)].

The stability region is a part of a complex plane consisting of those eigenvalues for which the technique produce a bounded solution.In the present meshless method of lines our numerical scheme is given in(11).We can investigate the stable and unstable eigenvalue spectrum for the given model by computing the eigenvalues of the matrix W,scaled by δt.

2.4 Choosing a good value of shape parameter

A variety of kernel functions are available in the literature.In our computation we used the multiquadrics,As usual these RBFs contain a shape parametercand solution accuracy greatly depends on this parameter.A variety of methods are available for choosing good value of shape parameter[Carlson and Foley(1991);Foley(1994);Rippa(1999);Trahan and Wyatt(2003);Fasshauer(2007);Scheuerer(2011);Uddin(2014)].A condition number may be used to quantify the sensitivity to perturbations of a linear system,and to estimate the accuracy of a computed solution.The conditioning results require that in order for the system matrix to be well-conditioned that the shape parameter and minimum separation distance be large.Obviously,both situations cannot occur at the same time.This observation has been referred to as the uncertainty principle[Schaback(1995)].Using this fact,the smallest errors occur when the condition number of the system matrix is approximately kept in the range 1013＜κ＜1015.The system matrix is decomposed as U,S,V=svd(Ai).Here svd is the singular value decomposition of the interpolation matrix Ai.U,V aren×northogonal matrices and S isn×ndiagonal matrix contains thensingular values of Ai,and κ =max(S)/min(S)is the condition number of the matrix Ai.When an acceptable value of shape parameter is returned by the above algorithm,then the svd is used to compute(Ai)−1=(USVT)−1=VS−1UT[see Trefethen and Bau III(1997)].Note that for orthogonal matrices the inverse of the matrix is equal to its transpose.Consequently,we can compute the weights wiin(9).

3 Numerical experiments

In this section,we apply the local meshless approximation method described in the above section to check the accuracy and validity of the present method for the wave equations given by.

which may be transformed into a system of two partial differential equations given by

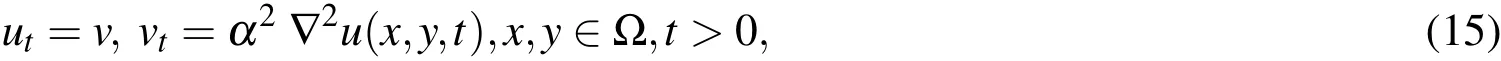
where α is speed of the wave.

3.1 The 2d membrane vibrating problem

We consider the 2D membrane vibration problem(14),which has an exact solution[Young,Gu,and Fan(2009)]

Tosolvetheproblem,weused theinitial conditionsu(x,y,0)=f(x,y),andut(x,y,0)=g(x,y,0),along with the boundary conditionsu=0.TheN=625 uniformly distributed centers in Ω,and 5≤n≤20 nodes in Ωiare used for solving the vibrating problem(14).The obtained results in the form of the L∞error norm,the condition number κ of the interpolation matrix,the shape parametercof the given kernel,and the computer time in seconds are shown in Table 1 and Figure 2.

Table 1:Numerical results with different stencil sizes n,corresponding to Problem 3.1:when N=625,t=1,δt=0.0001,α =1,domain[0,1]2.

3.2 Wave propagation problem in two-dimensional rectangular domain

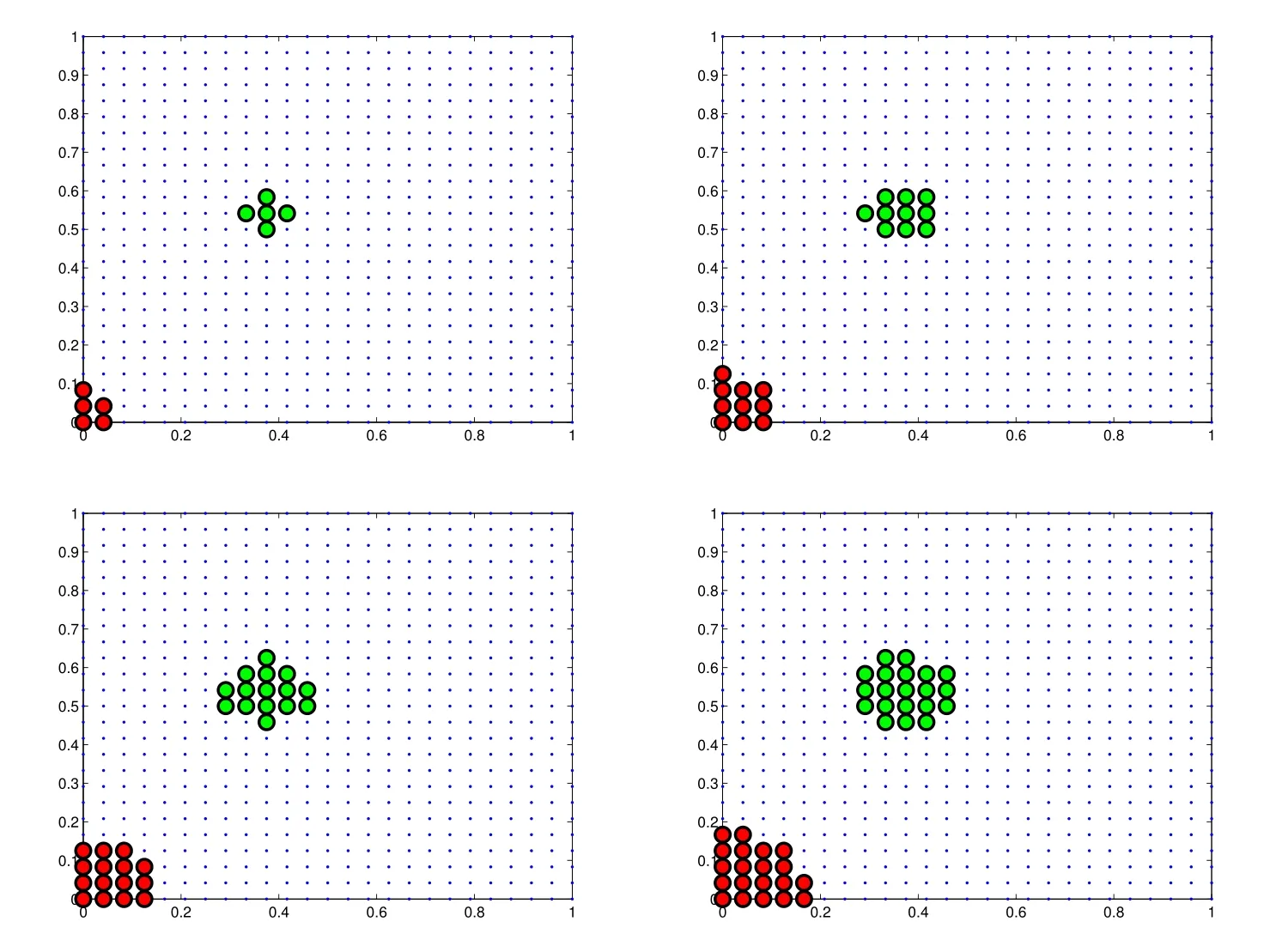
Figure 1:Centers distributions and a typical stencil associated with a boundary center(red)and an interior center(green),corresponding to Problem 3.1

Figure 2:L∞error norm versus number of nodes N in the domain[0,1]2 for a given stencil size n.

We consider the wave propagation problem in a rectangular domain.The initial hump displacement is selected at the center of the domain.The smooth wave front propagates towards the boundaries with a speed α=1.5.The hump shape of the initial displacement and the zero initial velocitiesu(x,y,0)=e(−4/25)(x2+y2),andut(x,y,0)=0,and the boundary conditionu=0 are used in the computation.TheN=1600 uniformly distributed centers in domain Ω =[−10,10]2andn=50 nodes in the local domain Ωiare used.The approximate solution by the present method in the form of wave propagation are shown in Figure 3.

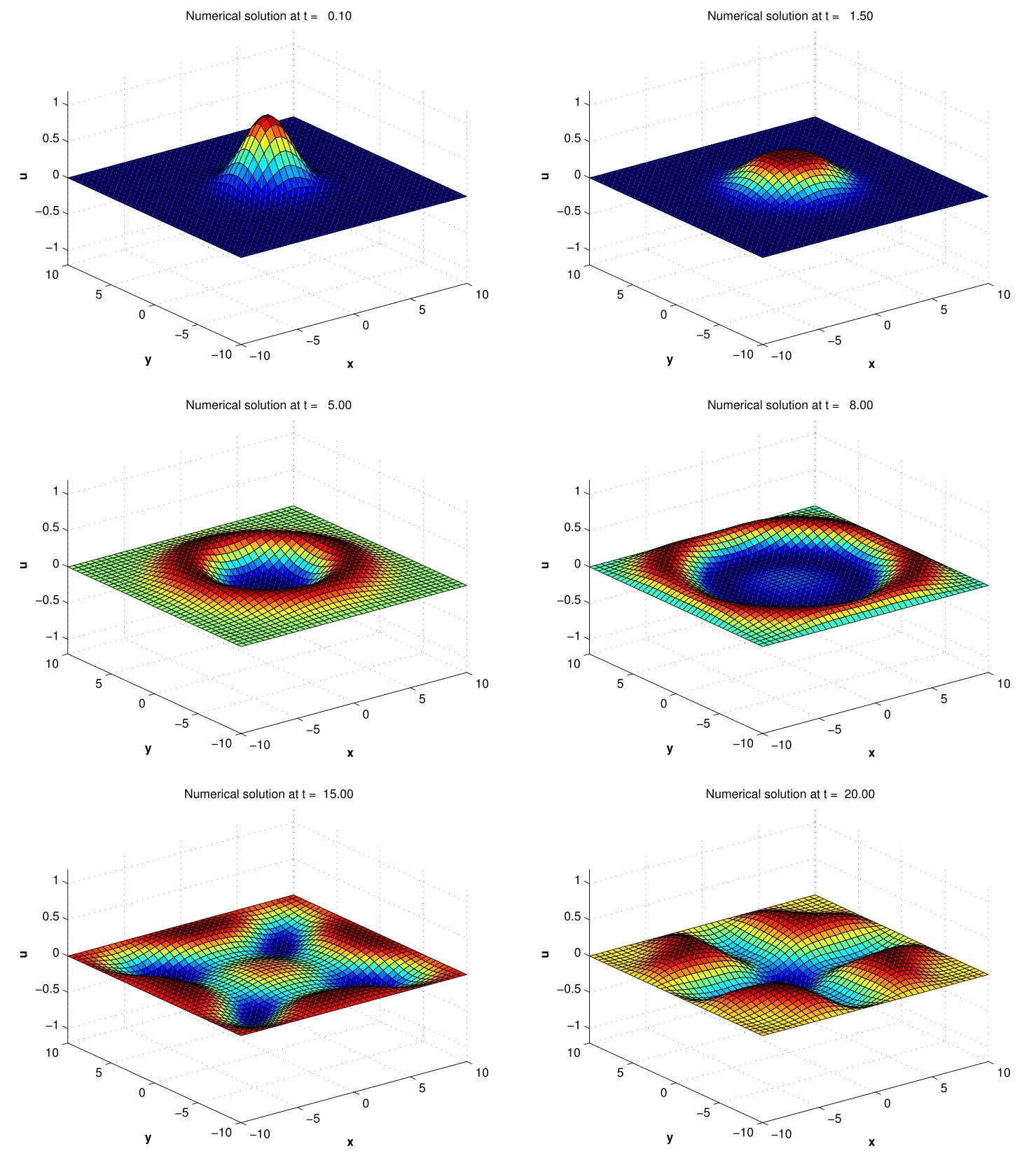
Figure 3:The evolution of wave propagation problem in rectangular domain with zero Dirichlet boundary conditions,corresponding to Problem 3.2.

Figure 4:The evolution of wave propagation problem in circular domain with zero Neumann boundary conditions,corresponding to Problem 3.3.

3.3 Wave propagation problem in two-dimensional circular domain

Next we consider the wave propagation problem in a circular domain.The initial hump displacement is selected at the center of the domain.The smooth wave front propagates towards the boundaries with a wave speed of α=1.5.The computational domain is selected as circular of radius 10 units.The the initial displace-ment and the zero initial velocities are selected asu(x,y,0)=e(−4/25)(x2+y2),andut(x,y,0)=0,along with the no flux boundary condition∇u.n=0 in the computations,where n is a unit normal vector to the circular boundary of the circular domain.The solution is again advanced in time by fourth-order Runge-Kutta scheme with time step size δt=0.001.We usedN=1600 uniformly distributed centers inΩ andn=50 in Ωi.The obtained results in form of wave propagation are shown in Figure 4.

3.4 Wave propagation problem in two-dimensional L-shaped domain

Here we consider the local meshless scheme for a more complicated wave propagation problem.In this problem we consider the L-shaped domain with non smooth boundary.We choose initial Gaussian hump displacement with a center at the point(-5,5).The computational domain is discretized withN=1541 equally spaced centers and the stencil sizen=50 are shown in Fig.6.The initial displacement and the zero initial velocity are selected asu(x,y,0)=e(−4/25)(x2+y2),andut(x,y,0)=0 respectively.The boundary condition is selected asu=0 on the boundary∂Ω.The local meshless scheme accurately simulate the wave propagation in the L-shaped domain with a wave speed of α=2.The simulation of wave propagation in the L-shaped domain is shown Fig.6 and the results of the present local meshless scheme is well agreed with work of Young,Gu,and Fan(2009).

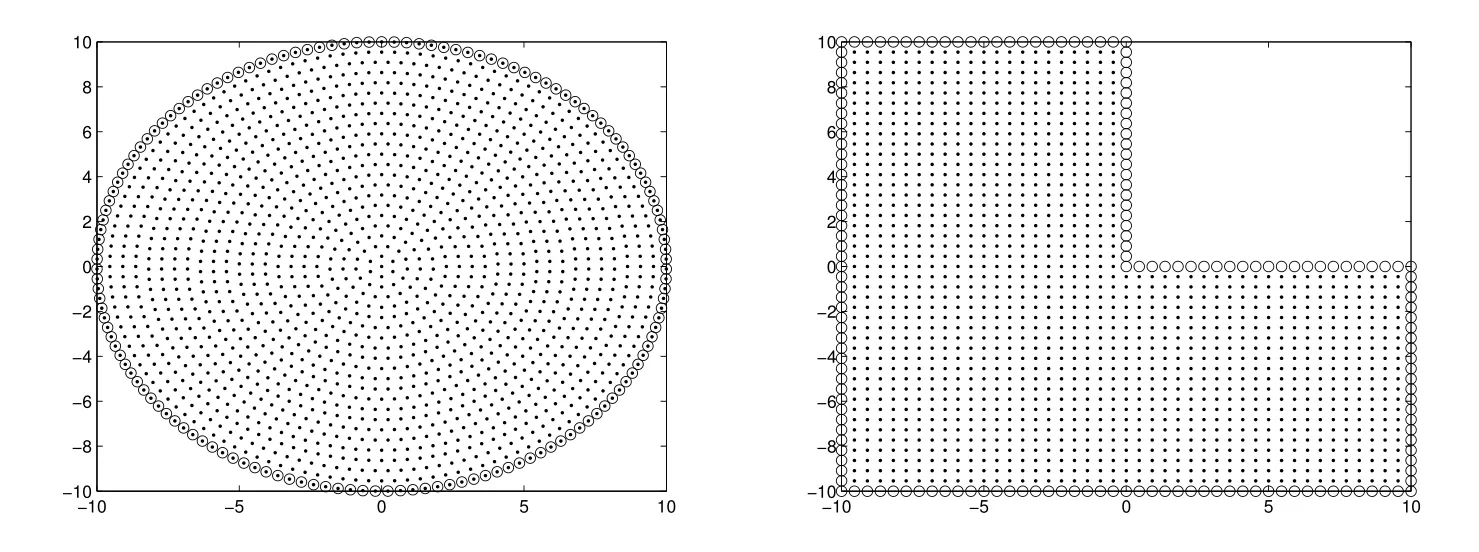
Figure 5:Centers distributions in circular and L-shaped domain,corresponding to Problems 3.3 and 3.4 respectively.

4 Conclusions

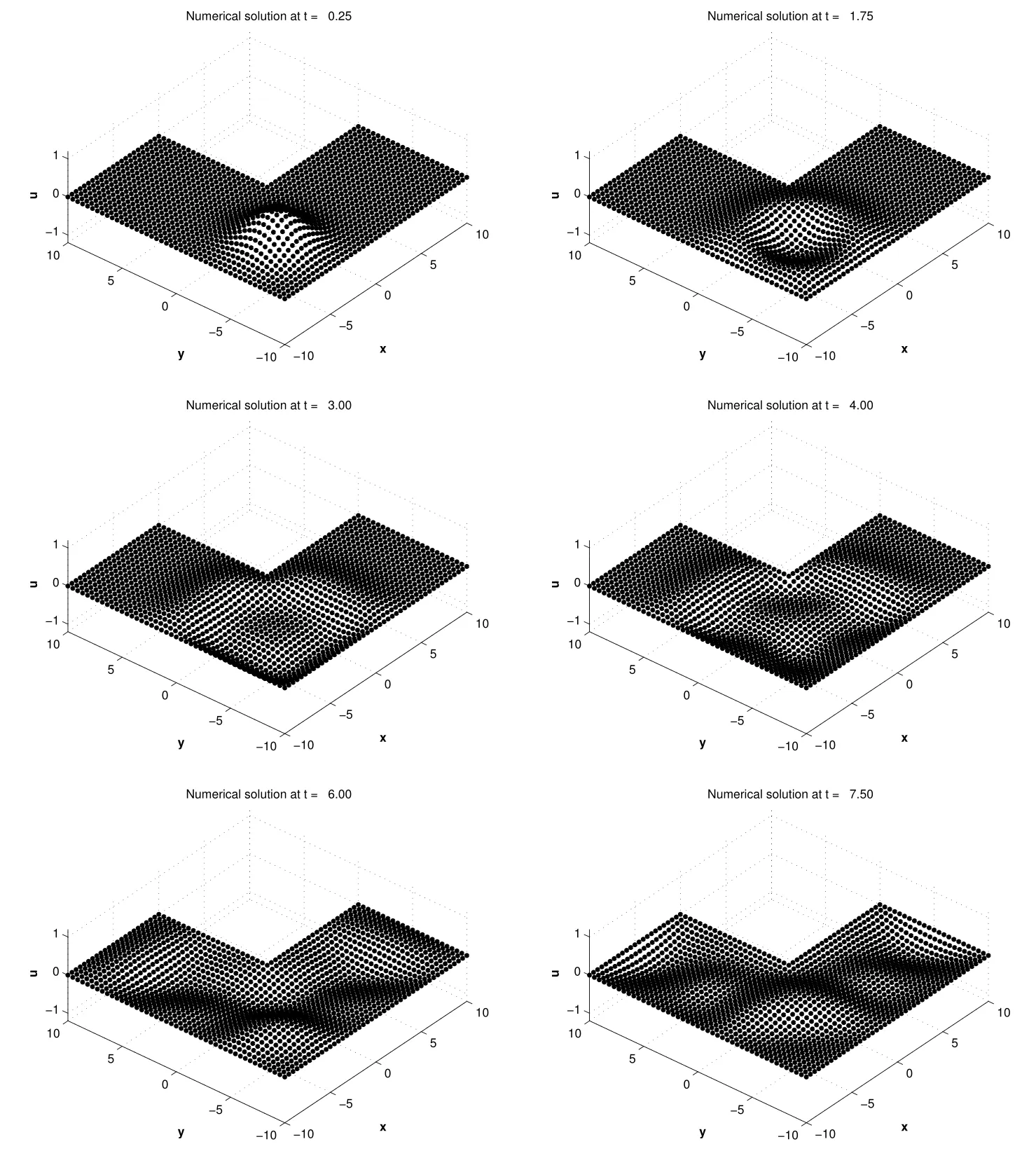
Figure 6:The evolution of wave propagation problem in L-shaped domain with zero Dirichlite boundary conditions,corresponding to Problem 3.4.

Inthiswork,thelocal kernel-based approximationschemefor solvingtime-dependent wave equations is applied.Due to the radial kernels the present local scheme has a great flexibility to solve multi-dimensional problems with arbitrary shaped domain.For large scale problems it is not possible to apply the global radial basis functions method which results a dense differentiation matrices.On the other hand the present local kernel based scheme has the capability of solving large scale problems because of solving small size linear systems in the local domain.The present lo-cal scheme is equally applicable for large scale time-dependent multi-dimensional problems with irregular shaped domain.

Acknowledgement:The second author is thankful to HEC Pakistan for financial support through Grant No.112-252337-2PS1-127(50021443).We are also thankful to the reviewers for their constructive comments.

Atluri,S.N.;Zhu,T.(1998): A new meshless local petrov-galerkin(mlpg)approach in computational mechanics.Computational mechanics,vol.22,no.2,pp.117–127.

Beatson,R.;Davydov,O.;Levesley,J.(2010):Error bounds for anisotropic rbf interpolation.Journal of Approximation Theory,vol.162,no.3,pp.512–527.

Beatson,R.K.;Light,W.;Billings,S.(2001):Fast solution of the radial basis function interpolation equations:Domain decomposition methods.SIAM Journal on Scientific Computing,vol.22,no.5,pp.1717–1740.

Brown,D.;Ling,L.;Kansa,E.;Levesley,J.(2005):On approximate cardinal preconditioning methods for solving pdes with radial basis functions.Engineering Analysis with Boundary Elements,vol.29,no.4,pp.343–353.

Buhmann,M.D.(2003):Radial basis functions:theory and implementations,volume 12.Cambridge university press.

Carlson,R.E.;Foley,T.A.(1991):The parameter r2in multiquadric interpolation.Computersamp;Mathematics with Applications,vol.21,no.9,pp.29–42.

Chandhini,G.;Sanyasiraju,Y.(2007): Local rbf-fd solutions for steady convection–diffusion problems.International Journal for Numerical Methods in Engineering,vol.72,no.3,pp.352–378.

Chen,W.;Fu,Z.-J.;Chen,C.-S.(2014):Recent advances in radial basis function collocation methods.Springer.

Cherrie,J.;Beatson,R.;Newsam,G.(2002): Fast evaluation of radial basis functions:Methods for generalized multiquadrics inrn.SIAM J.Sci.Comput.,vol.23,pp.1549–1571.

Chinchapatnam,P.P.;Djidjeli,K.;Nair,P.;Tan,M.(2009):A compact rbf-fd based meshless method for the incompressible navier-stokes equations.Proceedings of the Institution of Mechanical Engineers,Part M:Journal of Engineering for the Maritime Environment,vol.223,no.3,pp.275–290.

Dong,L.;Alotaibi,A.;Mohiuddine,S.;Atluri,S.(2014): Computational methods in engineering:a variety of primalamp;mixed methods,with globalamp;local interpolations,for well-posed or ill-posed bcs.CMES:Computer Modeling in Engineeringamp;Sciences,vol.99,no.1,pp.1–85.

Dormand,J.R.;Prince,P.J.(1980):A family of embedded runge-kutta formulae.Journal of computational and applied mathematics,vol.6,no.1,pp.19–26.

Elgohary,T.;Dong,L.;Junkins,J.;Atluri,S.(2014): Time domain inverse problems in nonlinear systems using collocationamp;radial basis functions.CMES:Computer Modeling in Engineeringamp;Sciences,vol.100,no.1,pp.59–84.

Fasshauer,G.E.(1999):Solving differential equations with radial basis functions:multilevel methods and smoothing.Advances in Computational Mathematics,vol.11,no.2-3,pp.139–159.

Fasshauer,G.E.(2007):Meshfree approximation methods with MATLAB,volume 6.World Scientific.

Fasshauer,G.E.;McCourt,M.J.(2012):Stable evaluation of gaussian radial basis function interpolants.SIAM Journal on Scientific Computing,vol.34,no.2,pp.A737–A762.

Fasshauer,G.E.;Zhang,J.G.(2007):On choosing “optimal”shape parameters for rbf approximation.Numerical Algorithms,vol.45,no.1-4,pp.345–368.

Floater,M.S.;Iske,A.(1996): Multistep scattered data interpolation using compactly supported radial basis functions.Journal of Computational and Applied Mathematics,vol.73,no.1,pp.65–78.

Foley,T.A.(1994):Near optimal parameter selection for multiquadric interpolation.Manuscript,Computer Science and Engineering Department,Arizona State University,Tempe.

Fu,Z.-J.;Chen,W.;Gu,Y.(2014): Burton–miller-type singular boundary method for acoustic radiation and scattering.Journal of Sound and Vibration,vol.333,no.16,pp.3776–3793.

Georgoulis,E.H.;Levesley,J.;Subhan,F.(2013): Multilevel sparse kernelbased interpolation.SIAM Journal on Scientific Computing,vol.35,no.2,pp.A815–A831.

Greengard,L.;Strain,J.(1991): The fast gauss transform.SIAM Journal on Scientific and Statistical Computing,vol.12,no.1,pp.79–94.

Gumerov,N.A.;Duraiswami,R.(2007):Fast radial basis function interpolation via preconditioned krylov iteration.SIAM Journal on Scientific Computing,vol.29,no.5,pp.1876–1899.

Haq,S.;Uddin,M.;Islam,S.U.(2009): Numerical solution of nonlinear schrodinger equations by collocation method using radial basis functions.CMES:Computer Modeling in Engineeringamp;Sciences,vol.44,no.2,pp.115–136.

Hardy,R.L.(1971): Multiquadric equations of topography and other irregular surfaces.Journal of geophysical research,vol.76,no.8,pp.1905–1915.

Hon,Y.;Schaback,R.;Zhou,X.(2003): An adaptive greedy algorithm for solving large rbf collocation problems.Numerical Algorithms,vol.32,no.1,pp.13–25.

Kansa,E.;Hon,Y.(2000): Circumventing the ill-conditioning problem with multiquadric radial basis functions:applications to elliptic partial differential equations.Computersamp;Mathematics with applications,vol.39,no.7,pp.123–137.

Kansa,E.J.(1990):Multiquadrics-a scattered data approximation scheme with applications to computational fluid-dynamics-i surface approximations and partial derivative estimates.Computersamp;Mathematics with applications,vol.19,no.8,pp.127–145.

Kansa,E.J.(1990):Multiquadrics-a scattered data approximation scheme with applications to computational fluid-dynamics-ii solutions to parabolic,hyperbolic and elliptic partial differential equations.Computersamp;mathematics with applications,vol.19,no.8,pp.147–161.

Levesley,J.;Sun,X.(2005):Approximation in rough native spaces by shifts of smooth kernels on spheres.Journal of Approximation Theory,vol.133,no.2,pp.269–283.

Li,J.;Hon,Y.(2004):Domain decomposition for radial basis meshless methods.Numerical Methods for Partial Differential Equations,vol.20,no.3,pp.450–462.

Lin,J.;Chen,W.;Chen,C.;Jiang,X.(2013): Fast boundary knot method for solving axisymmetric helmholtz problems with high wave number.CMESCOMPUTER MODELING IN ENGINEERINGamp;SCIENCES,vol.94,no.6,pp.485–505.

Ling,L.;Schaback,R.(2008): Stable and convergent unsymmetric meshless collocation methods.SIAM Journal on Numerical Analysis,vol.46,no.3,pp.1097–1115.

Micchelli,C.A.(1984):Interpolation of scattered data:distance matrices and conditionally positive definite functions.Springer.

Rippa,S.(1999):An algorithm for selecting a good value for the parameter c in radial basis function interpolation.Advances in Computational Mathematics,vol.11,no.2-3,pp.193–210.

(2005):A radial basis function collocation approach in computational fl uid dynamics.Computer Modelling in Engineeringamp;Sciences,vol.7,pp.185–193.

(2006): Meshfree explicit local radial basis function collocation method for diffusion problems.Computersamp;Mathematics with applications,vol.51,no.8,pp.1269–1282.

Sarra,S.A.(2012):A local radial basis function method for advection–diffusion–reaction equations on complexly shaped domains.Applied Mathematics and Computation,vol.218,no.19,pp.9853–9865.

Sarra,S.A.;Kansa,E.J.(2009):Multiquadric radial basis function approximation methods for the numerical solution of partial differential equations.Advances in Computational Mechanics,vol.2,no.2.

Schaback,R.(1995): Error estimates and condition numbers for radial basis function interpolation.Advances in Computational Mathematics,vol.3,no.3,pp.251–264.

Schaback,R.(2007):Convergence of unsymmetric kernel-based meshless collocation methods.SIAM Journal on Numerical Analysis,vol.45,no.1,pp.333–351.

Schaback,R.;Wendland,H.(2000): Adaptive greedy techniques for approximate solution of large rbf systems.Numerical Algorithms,vol.24,no.3,pp.239–254.

Scheuerer,M.(2011):An alternative procedure for selecting a good value for the parameter c in rbf-interpolation.Advances in Computational Mathematics,vol.34,no.1,pp.105–126.

Shampine,L.F.;Gordon,M.K.(1975):Computer solution of ordinary differential equations:the initial value problem.WH Freeman San Francisco.

Shan,Y.;Shu,C.;Lu,Z.(2008): Application of local mq-dq method to solve 3d incompressible viscous flows with curved boundary.Computer modeling in engineering and sciences,vol.25,no.2,pp.99.

Shibahara,M.;Atluri,S.(2011):The meshless local petrov-galerkin method for the analysis of heat conduction due to a moving heat source,in welding.International Journal of Thermal Sciences,vol.50,no.6,pp.984–992.

Shu,C.;Ding,H.;Yeo,K.(2003): Local radial basis function-based differential quadrature method and its application to solve two-dimensional incompressible navier-stokes equations.Computer Methods in Applied Mechanics and Engineering,vol.192,no.7,pp.941–954.

Sladek,J.;Stanak,P.;Han,Z.;Sladek,V.;Atluri,S.(2013):Applications of the mlpg method in engineeringamp;sciences:a review.Comput.Model.Eng.Sci,vol.92,pp.423–475.

Stevens,D.;Power,H.;Lees,M.;Morvan,H.(2009):The use of pde centres in the local rbf hermitian method for 3d convective-diffusion problems.Journal of Computational Physics,vol.228,no.12,pp.4606–4624.

Tolstykh,A.;Shirobokov,D.(2003): On using radial basis functions in a“f inite difference mode”with applications to elasticity problems.Computational Mechanics,vol.33,no.1,pp.68–79.

Tolstykh,A.I.(2000):On using rbf-based differencing formulas for unstructured and mixed structured-unstructured grid calculations.InProceedings of the 16th IMACS World Congress,Lausanne,volume 228,pp.4606–4624.

Trahan,C.J.;Wyatt,R.E.(2003): Radial basis function interpolation in the quantum trajectory method:optimization of the multi-quadric shape parameter.Journal of Computational Physics,vol.185,no.1,pp.27–49.

Trefethen,L.N.(2000):Spectral methods in MATLAB,volume 10.Siam.

Trefethen,L.N.;Bau III,D.(1997):Numerical linear algebra,volume 50.Siam.

Uddin,M.(2013):Rbf-ps scheme for solving the equal width equation.Applied Mathematics and Computation,vol.222,pp.619–631.

Uddin,M.(2014):On the selection of a good value of shape parameter in solving time-dependent partial differential equations using rbf approximation method.Applied Mathematical Modelling,vol.38,no.1,pp.135–144.

Uddin,M.;Haq,S.(2013):On the numerical solution of generalized nonlinear schrodinger equation using rbfs.Miskolc Mathematical Notes,vol.14,no.3,pp.1067–1084.

Voller,V.;Vertnik,R.;Šarler,B.(2006): Meshless local radial basis function collocation method for convective-diffusive solid-liquid phase change problems.International Journal of Numerical Methods for Heatamp;Fluid Flow,vol.16,no.5,pp.617–640.

Wendland,H.(1995): Piecewise polynomial,positive definite and compactly supported radial functions of minimal degree.Advances in computational Mathematics,vol.4,no.1,pp.389–396.

Wendland,H.(2002):Fast evaluation of radial basis functions:Methods based on partitionof unity.InApproximation Theory X:Wavelets,Splines,and Applications,pp.473–483.Citeseer.

Wendland,H.(2004):Scattered data approximation,volume 17.Cambridge university press.

Wong,A.;Hon,Y.;Li,T.;Chung,S.;Kansa,E.(1999):Multizone decomposition for simulation of time-dependent problems using the multiquadric scheme.Computersamp;Mathematics with Applications,vol.37,no.8,pp.23–43.

Wright,G.B.;Fornberg,B.(2006): Scattered node compact finite differencetype formulas generated from radial basis functions.Journal of Computational Physics,vol.212,no.1,pp.99–123.

Xiao,J.;McCarthy,M.(2003):A local heaviside weighted meshless method for two-dimensional solids using radial basis functions.Computational Mechanics,vol.31,no.3-4,pp.301–315.

Yao,G.;Šarler,B.;Chen,C.(2011):A comparison of three explicit local meshless methods using radial basis functions.Engineering Analysis with Boundary Elements,vol.35,no.3,pp.600–609.

Yao,G.;Sarler,B.etal.(2010):A comparativestudy of global and local meshless methods for diffusion-reaction equation.CMES:Computer Modeling in Engineeringamp;Sciences,vol.59,no.2,pp.127–154.

Young,D.;Gu,M.;Fan,C.(2009):The time-marching method of fundamental solutions for wave equations.Engineering analysis with boundary elements,vol.33,no.12,pp.1411–1425.

1Department of Basics Sciences,UET,Peshawar.

2Corresponding author E-mail:marjan@uetpeshawar.edu.pk;marjankhan1@hotmail.com