Meshless Local Petrov-Galerkin Method for Rotating Euler-Bernoulli Beam

V.Panchore,R.Ganguliand S.N.Omkar

Meshless Local Petrov-Galerkin Method for Rotating Euler-Bernoulli Beam

V.Panchore1,R.Ganguli2and S.N.Omkar3

Free vibration problem of a rotating Euler-Bernoulli beam is solved with a truly meshless local Petrov-Galerkin method.Radial basis function and summation of two radial basis functions are used for interpolation.Radial basis function satisfies the Kronecker delta property and makes it simpler to apply the essential boundary conditions.Interpolation with summation of two radial basis functions increases the node carrying capacity within the sub-domain of the trial function and higher natural frequencies can be computed by selecting the complete domain as a sub-domain of the trial function.The mass and stiffness matrices are derived and numerical results for frequencies are obtained for a fixed-free beam and hinged-free beam simulating hingeless and articulated helicopter blades.Stiffness and mass distribution suitable for wind turbine blades are also considered.Results show an accurate match with existing literature.

Petrov-Galerkin Method,Radial Basis Function,Rotating Euler-Bernoulli Beam,Free Vibration.

1 Introduction

In conventional finite element method,considerable time is required to mesh the structure.Problems with large deformation lead to unreliable results and higher order derivatives of the field variable are discontinuous at the element boundaries.Meshless method is an option to overcome such problems,where the formulation is based on the nodal distribution within the structure.A meshless local Petrov-Galerkin method does not require a background mesh while formulating shape functions and integrating the weak form.Unlike other meshless methods,it is a truly meshless method[Atluri et al.（2013）].

The Galerkin method yields a weak form of the problem,where basis functions to construct test function and basis functions to construct trial function are chosen to be the same and yield a system of symmetric matrices.In contrast,the Petrov-Galerkin method,where trial function and test functions are constructed using different basis functions yields a system of unsymmetric matrices.

A rotating Euler-Bernoulli beam equation contains a centrifugal force term which varies along the length of the beam[Johnson （1980）;Bisplinghoff,Ashley,and Halfman （1996）;Bramwell,Done,and Balmford （2001）]and makes it difficult to get the analytical solutions.Analytical solution can be obtained assuming the centrifugal force to be constant along the length of the beam[Bokaian （1990）].Semianalytical solutions are obtained using Frobenius method[Giurgiutiu and Stafford（1977）;Banerjee（2000）].Solution of a rotating Euler-Bernoulli beam problem is generally obtained using the finite element method[Putter and Manor（1978）;Hoa（1979）;Bauchau and Hong （1987）;Chung and Yoo （2002）].This problem was solved using Galerkin finite element method[Nagaraj and Shanthakumar（1975）],using variable order finite element method[Hodges and Rutkowski（1981）],and using spectral finite element method[Wang and Wereley （2004）;Vinod,Gopalakrishnan,and Ganguli（2007）].Gunda and Ganguli（2007）found that stiff string basis functions can accelerate the convergence of rotating beam finite element method.In a further paper[Gunda,Gupta,and Ganguli（2008）]they found that hybrid combinations of polynomials and the stiff string basis functions are very useful for fast convergence.Sushma and Ganguli（2012）showed that a collocation approach which satisfies the governing differential equation of the rotating beam yields superior basis functions.These works clearly showed that basis functions play an important role in the convergence of finite element methods for rotating beams.This naturally led to the idea to use meshless methods which completely depend on basis functions and avoid the problem of mesh generation.Considerable research is still required in obtaining the rotating beam solution with analytical and numerical techniques.

Moving least squares interpolation functions do not satisfy the Kronecker delta property and essential boundary conditions are enforced using penalty parameters and Lagrange multiplier method[Liu （2003）].A new weighing function was used for moving least squares interpolation which almost satisfies the Kronecker delta property[MostandBucher（2005）].Radial basis functions do satisfy the Kronecker delta property and essential boundary conditions can be enforced easily.Moving Kriging interpolation is also an option with meshless methods and it satisfies the Kronecker delta property[Hu,Wang,Li,Gu,and Han （2014）].Radial basis func-tions were used as trial functions for solving ill-posed time-domain inverse problems,where collocation method yields a weak form of the problem and solutions were found to be independent of the accurate initial guess[Elgohary,Dong,Junkins and Atluri（2014）],a similar combination of radial basis function and collocation method was used for solving nonlinear initial value problems[Elgohary,Dong,Junkins and Atluri（2014）],and for solving the orbit propagation of the two-body problem[Elgohary,Junkins and Atluri（2015）].

Diffused element method was introduced to overcome the drawbacks of the finite element method and required only spatial location of the nodes[Nayroles,Touzot,and Villon （1992）].Element free Galerkin method which requires a background mesh showed improvements over the diffused element method and used moving least square interpolation[Belytschko,Lu,and Gu （1994）].Weak form of Galerkin method is solved with meshfree method using moving Kriging interpolation[Hu,Wang,Li,Gu,and Han （2014）].

Meshless local Petrov-Galerkin method is suitable to different test functions and trial functions,six different formulation were discussed based on the combinations of test functions and trial functions[Atluri and Shen （2002）;Atluri（2004）].MostlyC0andC1continuous problems were solved using meshless local Petrov-Galerkin method[Andreaus,Batra,and Porfiri（2005）;Gu and Liu （2001）;Long and Atluri（2002）].In literature,non-rotating beam equations were solved using moving least squares interpolation[Atluri,Cho,and Kim （1999）]and radial basis function interpolation[Raju,Phillips and Krishnamurthy （2004）].Various methods are derived from the meshless local Petrov-Galerkin method[Atluri（2004）],a meshless local Petrov-Galerkin mixed finite difference method was used for solving solid mechanics problems[Atluri,Liu and Han （2006）]and a meshless local Petrov-Galerkin mixed collocation method was used for solving elasticity problems[Atluri,Liu and Han （2006）].Meshless local Petrov-Galerkin method was also applied to the heat transfer problem[Tian and Rao （2012）].

In this paper,we solve the free vibration problem of a rotating Euler-Bernoulli beam using meshless local Petrov-Galerkin method.Radial basis function and summation of two radial basis functions are used for interpolation.Summation of two radial basis functions approximation increases the node carrying capacity within the sub-domain of the trial function and higher natural frequencies can be computed using only one sub-domain of the trial function.For fixed parameters,we get 7 and 10 nodes with one function approximation and summation of two functions approximation,respectively.Equal nodal density is assumed in each sub-domain of the trial function for accuracy[Belinha （2014）].Results are compared with literature and we find a very accurate match with existing results.

2 Rotating Euler-Bernoulli beam differential equation

Governing differential equation of a rotating Euler-Bernoulli uniform beam is given by[Johnson （1980）]

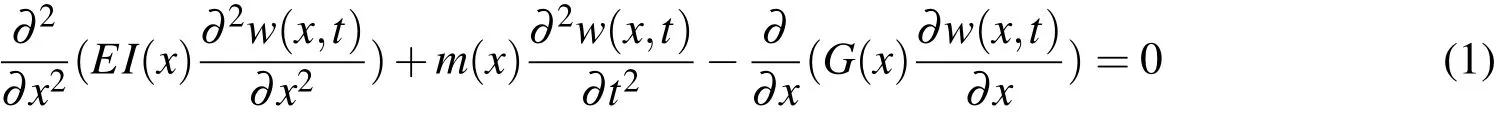
Here,EI（x）andm（x）are the stiffness and mass distribution along the length of the beam,wis the transverse displacement andG（x）is the centrifugal force and it is given by

where,Ω is the angular velocity andRis the radius of the rotating beam.Mass and stiffness distributions along the length of the beam are given by

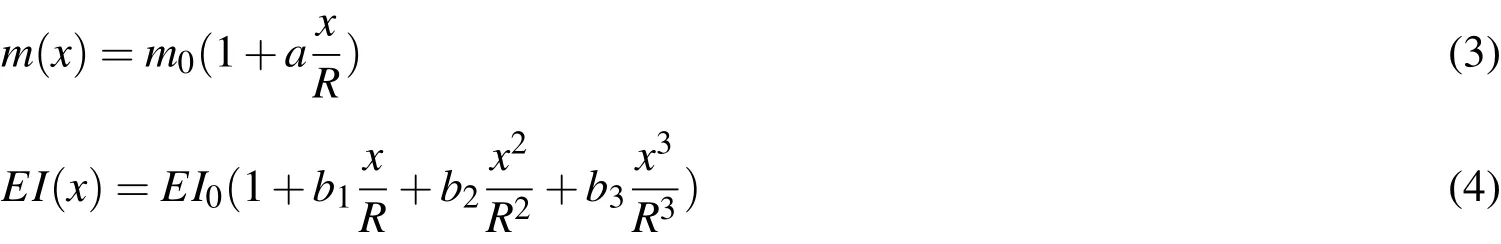
Here,EI0andm0are the stiffness and mass distribution at the root of the beam.Parametersa,b1,b2,andb3can be chosen independently[Wright et al. （1982）].We get singularity fora=-1 atx=R,so we reach a conditiona/=-1.Figure 1 shows a non-uniform rotating Euler-Bernoulli beam.

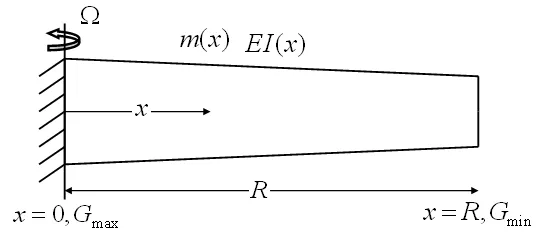
Figure 1:A rotating Euler-Bernoulli beam.

For free vibration problem,we assume solutionw（x,t）=eiωt¯wto get

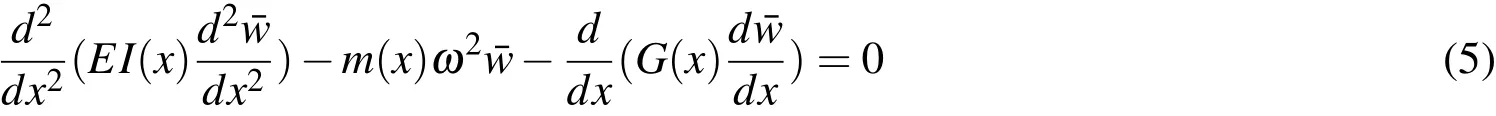
where,ω is the natural frequency.Weak form of equation （5）is given by

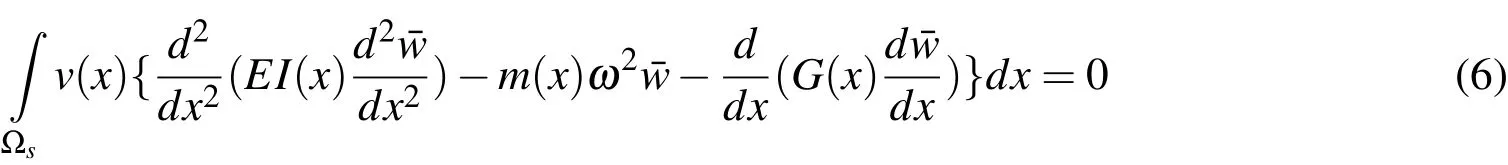
where,v（x）is the test function.

3 Weak formulation for the meshless local Petrov-Galerkin method

The formulation of a meshless local Petrov-Galerkin method is based on the nodal test function.Weak formulation is integrated over the sub-domain of the nodal test function.Equations can be written for each nodal test function sub-domain.Figure 2 shows nodal distribution within a a rotating Euler-Bernoulli beam.Here,Ω（i）sis the sub-domain of the nodal test function and Γ（i）sis the boundary of the nodal test function.2Svis the length of the sub-domain of the nodal test function and 2Stis the length of the sub-domain of the trial function.A similar approach is used in literature for a non-rotating Euler-Bernoulli beam[Raju,Phillips and Krishnamurthy （2004）].

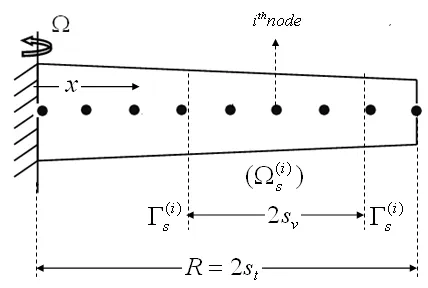
Figure 2:Nodal distribution for a meshless local Petrov-Galerkin method.

Equation （6）can be written for a meshless local Petrov-Galerkin method as

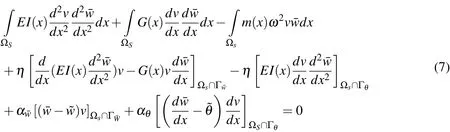
where,α¯wand αθare penalty parameters to apply the essential boundary conditions.˜wand˜θ are the essential boundary conditions.η is a unit vector and it is positive on the right hand side of the sub-domain of the nodal test function.Ωs∩Γ¯wand Ωs∩Γθrepresent the intersection of the sub-domain of the nodal test function with the boundary,where deflection and slope are prescribed.

4 Radial basis function interpolation for meshless method

For shape function formulation,we assume the transverse displacement as[Raju,Phillips and Krishnamurthy （2004）]

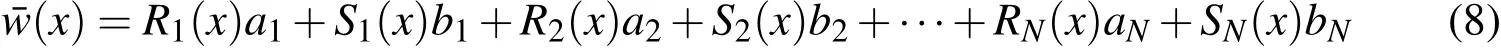
where,Nis the number of nodes,anda1,b1,a2,b2, ···,aN,bNare arbitrary constants.

Equations （9a）and （9b）show the two approximations used for interpolation,one function and summation of two functions,respectively.

Here,Rj（x）is the radial basis function andSj（x）is the derivative of the radial basis function.Values ofcandstare user defined.Approximation with summation of two functions increases the node carrying capacity in one sub-domain of the trial function.

We write slope by differentiating equation （8）with respect toxas

We can rewrite the transverse displacement as

where,

and

We can rewrite slope as

Where,

Substituting displacement and slope values at the nodal points in equation （12）and（15）,we get

where,

and

Here,w1,θ1,w2,θ2,···wNand θNare nodal degrees of freedom.

We can rewrite equation （17）as

From equation （12）and equation （20）,we get

where,[H（x）]is shape function vector.

[H（x）]（1,2N）=[Q（x）]（1,2N）[QM]-1（2N,2N）（23）

Approximate trial function can be written as

Figures 3a and 3b show the variation of the shape function and its derivative.

Figure 3a:Variation of shape function.

Figure 3b:Variation of shape function derivative.

5 Test function for a meshless local Petrov-Galerkin method.

Basis function for the test function can be chosen arbitrarily such that it is zero outside the sub-domain of the nodal test function and it is given by[Raju,Phillips and Krishnamurthy （2004）]

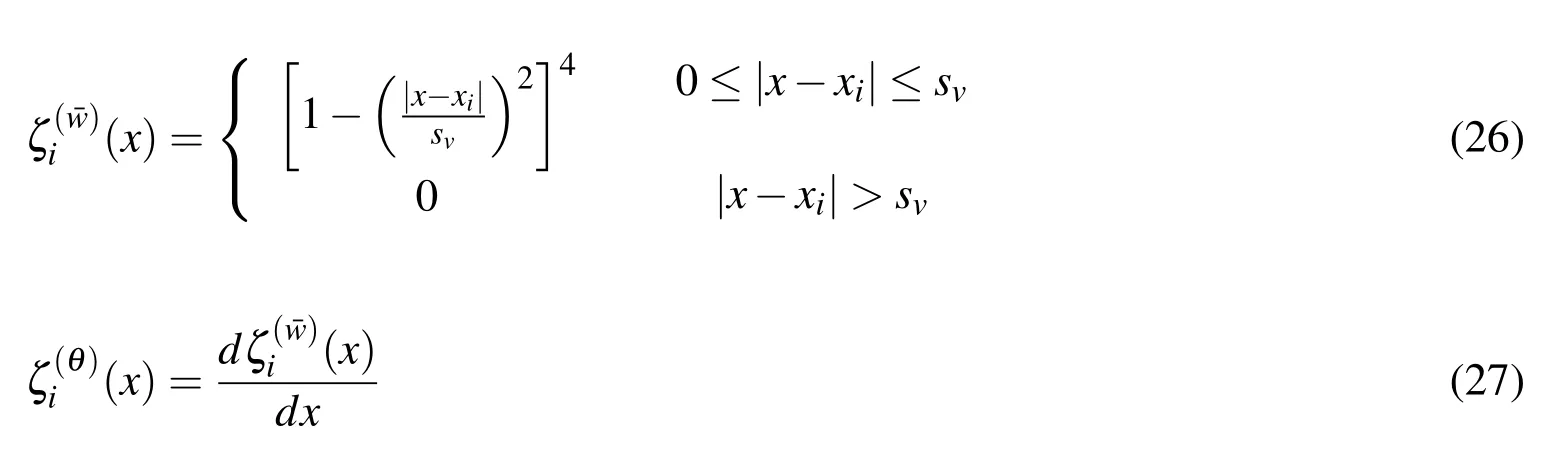
Figure 4 shows the variation of basis function for two sub-domain lengths of the test function 2dand 4d,where,dis the distance between two consecutive nodes.Figure 5 shows the overlapping of the sub-domains of the test function.

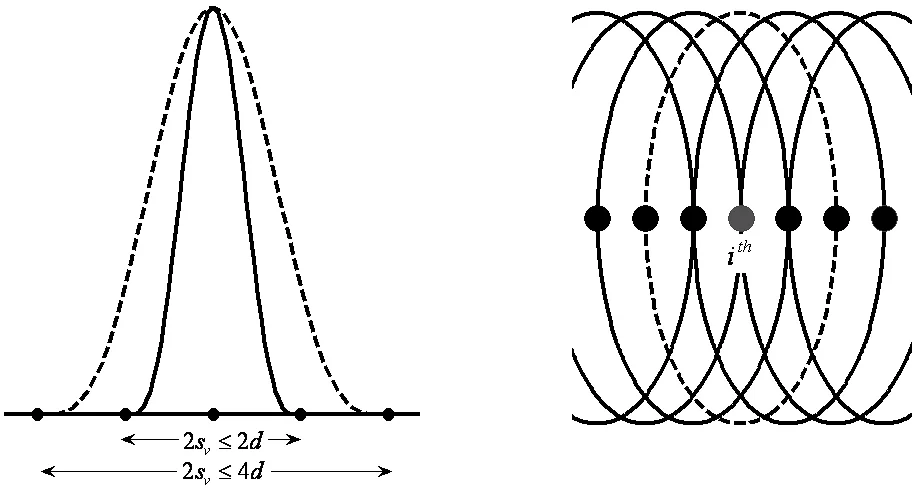
Figure 4:Variation of test function within the Figure 5.

Figure 5:Overlapping of the sub-domain sub-domain.

6 Formulation for the meshless local Petrov-Galerkin method

For each sub-domain of the nodal test functions,we can write algebraic equations and get the global stiffness matrix and the global mass matrix.Stiffness matrix is constructed using two terms.First term contains nodes contributing within the domain and the second term contains nodes contributing to the boundary.Equations can be written based on the nodal test function and spatial location of the node is required.Using approximate trial and test function we can write equation （7）for each nodal test function as

Stiffness matrix for the nodes within the domain is given by

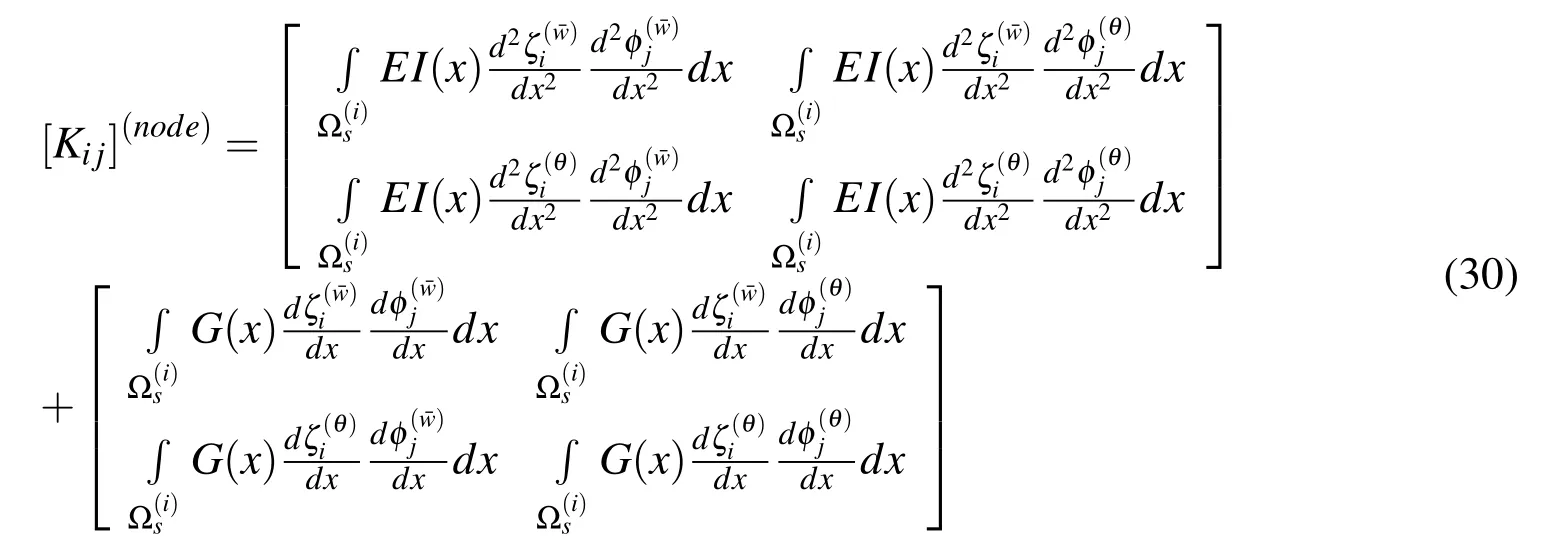
The second matrix on the right hand side of the above equation represents the cen-trifugal stiffening term.Stiffness matrix for the nodes contributing to the boundary is given by

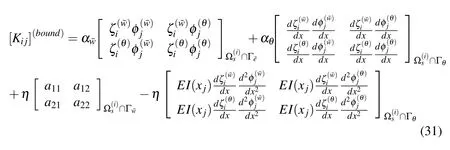
where,

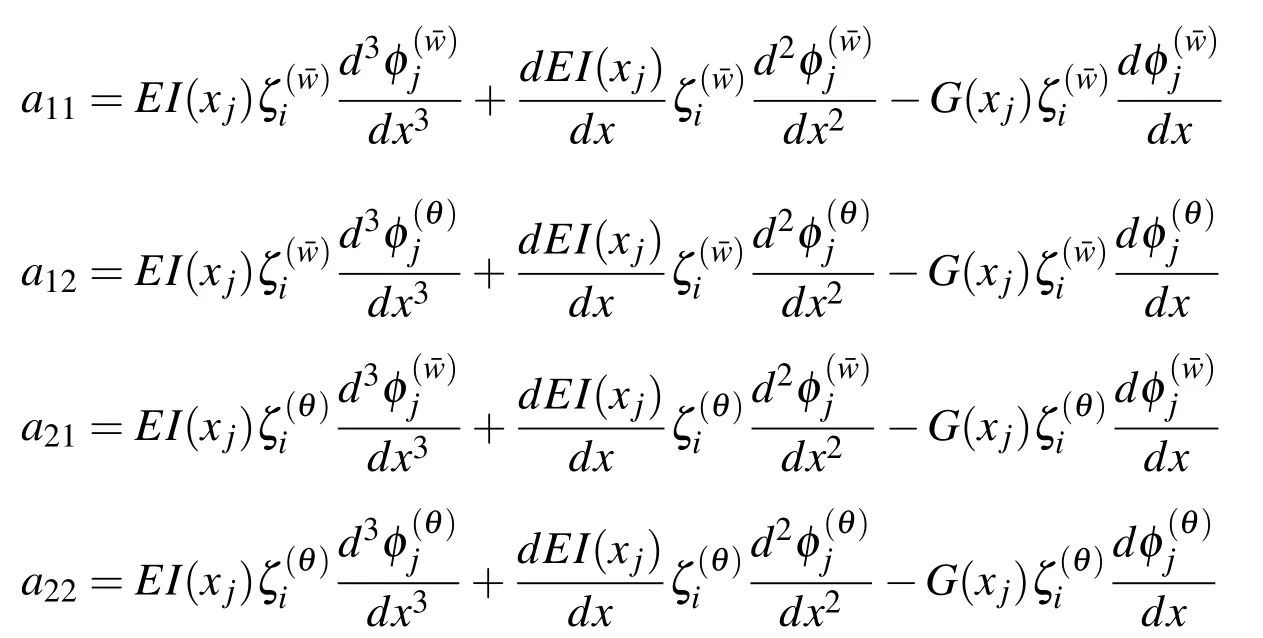
Mass matrix is given by

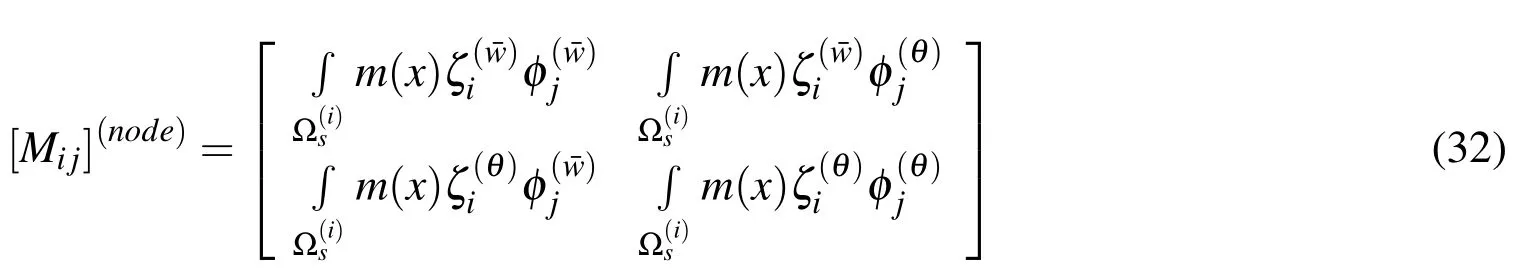
For free vibration problem we can write

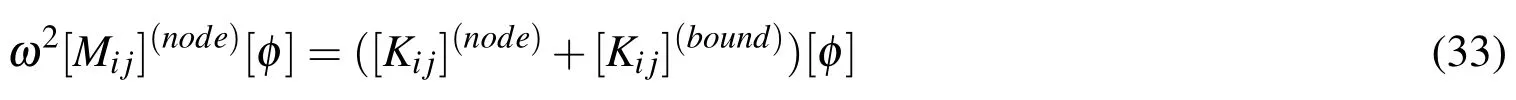
We get the natural frequencies and the mode shapes using equation （31）.

In this work,essential boundary conditions can be applied using the penalty parameters.Radial basis function satisfies the Kronecker delta property and boundary conditions can be applied directly as well.First two terms of equation （31）can be removed with direct application of the essential boundary conditions.

7 Results and Discussion

In this section,we compare our results with existing literature.Two types of results are discussed.First with fixed-free boundary condition,which is generally compared in the literature and second with hinged-free boundary condition which is also shown in the classical text book of aeroelasticity[Bisplinghoff,Ashley,and Halfman （1996）].Fixed-free boundary condition represents a hingeless helicopter rotor blade and hinged-free boundary condition represent an articulated rotor blade.

7.1 Fixed-Free Boundary Conditions

A rotating fixed-free beam is used.Inputs for the results are,m0=6.4636kg/m,Ω=40.12rad/sec,R=4.9378m,and=0.008345,[Zhang （2001）].Here,non-dimensional rotating frequency η and non-dimensional rotating speedsis given byHerenis the number of sub-domains of the trial function,which is set ton=1 for all the results andpis the number of nodes in the sub-domain of the trial function.n≥2 can be achieved by overlapping of the sub-domain of the trial function.

Tables 1 and 2 show the results of a uniform non-rotating and uniform rotating beam,respectively.Figures 6（a）and 6（b）show the mode shapes of a uniform nonrotating and uniform rotating beam,respectively.

Note that withc=1 and 2st=R,we can get 7 and 10 number of nodes in one sub-domain of the trial function with one function and summation of two functions approximation,respectively.

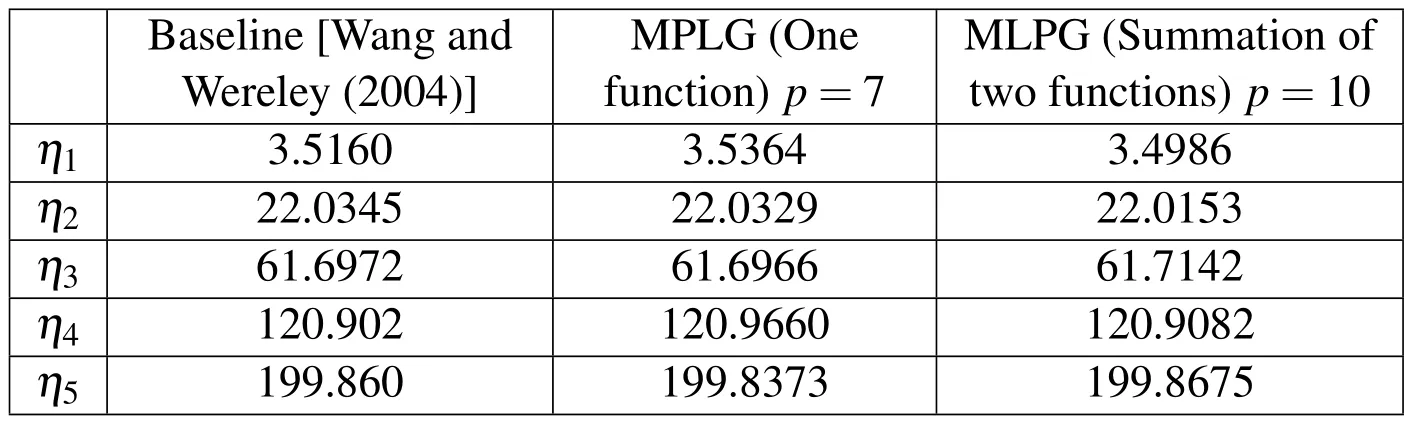
Table 1:Natural frequencies of a uniform beam for non-dimensional rotating speed s=0.

For a non-uniform rotating Euler-Bernoulli beam mass and stiffness distribution are given by[Wright et al.（1982）]

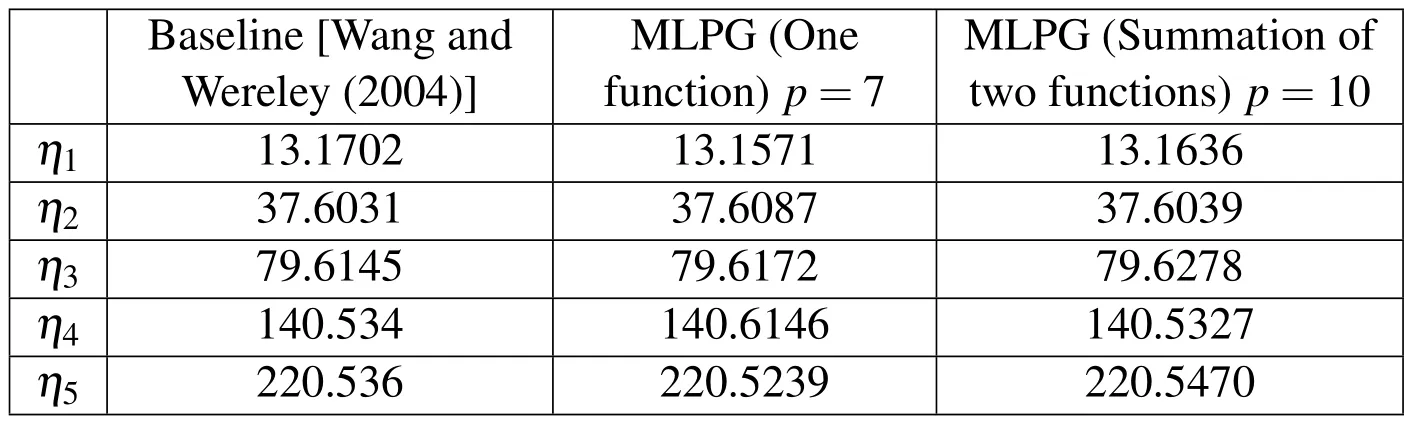
Table 2:Natural frequencies of a uniform beam for non-dimensional rotating speed s=12.

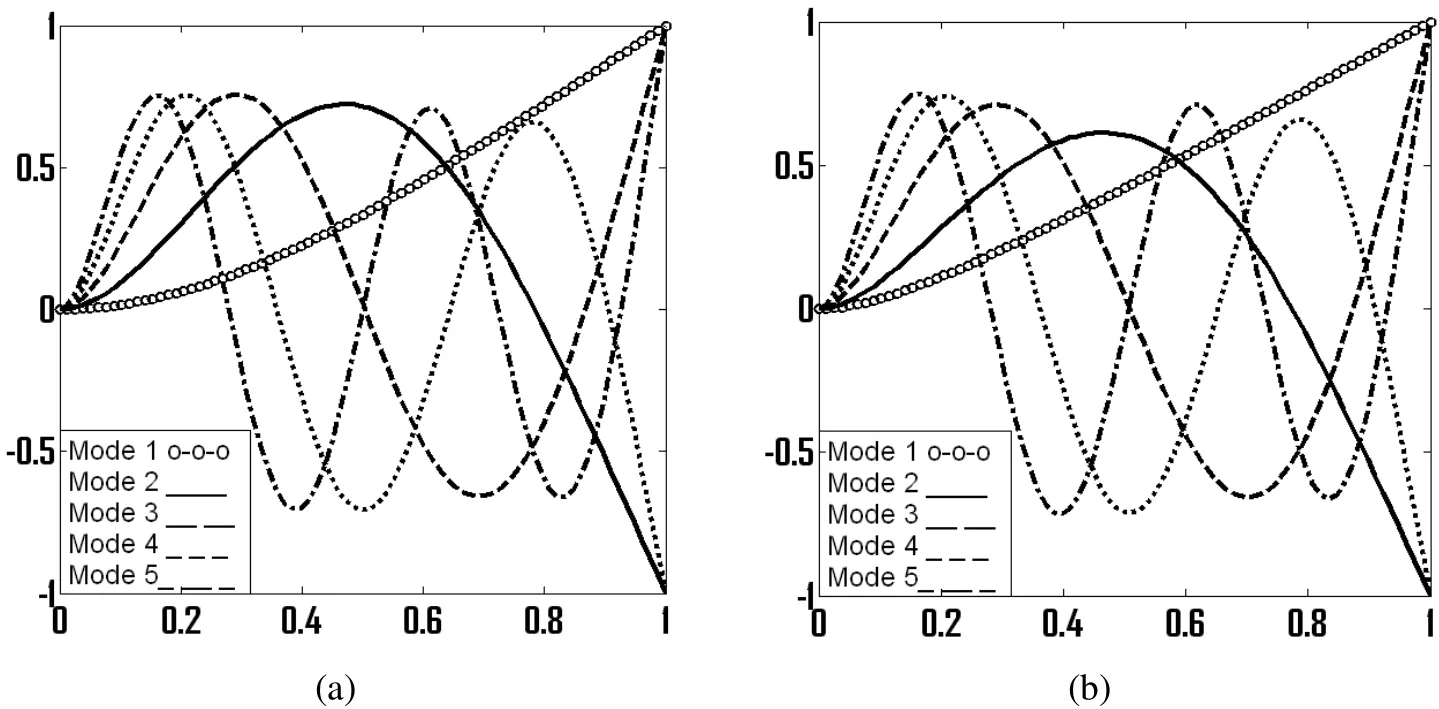
Figure 6:Mode shapes of a uniform beam for rotating speed s=0 （left）and s=12（right）.

This mass and stiffness distribution generally represents a wind turbine blade.Tables 3 and 4 show the results of a non-uniform non-rotating and non-uniform rotating beam,respectively.Figures 7（a）and 7（b）show the mode shapes of a nonuniform non-rotating and non-uniform rotating beam,respectively.

A non-uniform beam with cubic stiffness distribution is given by[Wright et al.（1982）]

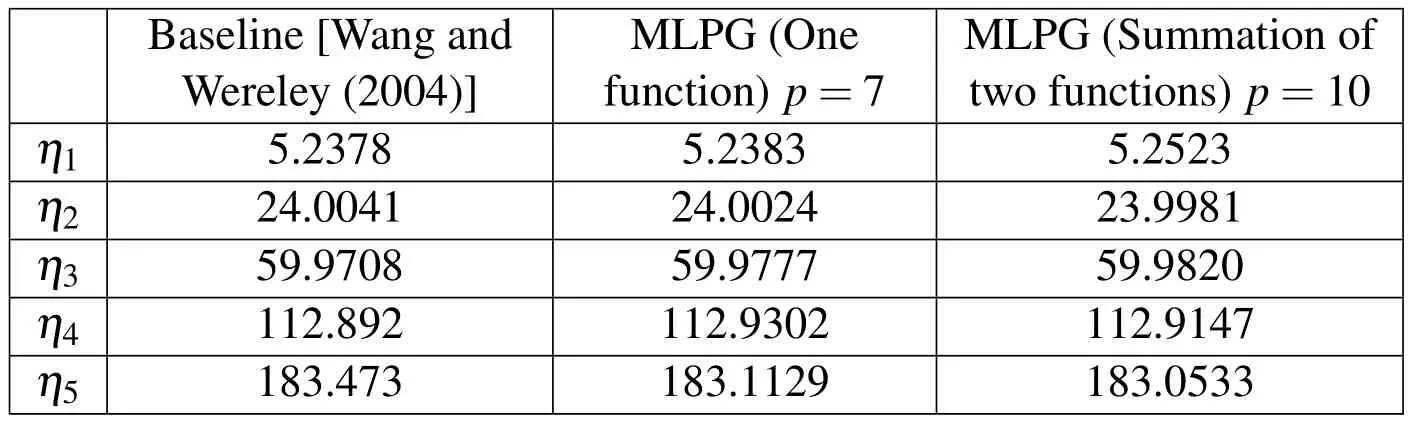
Table 3:Natural frequencies of a non-uniform beam for non-dimensional rotating speed s=0.

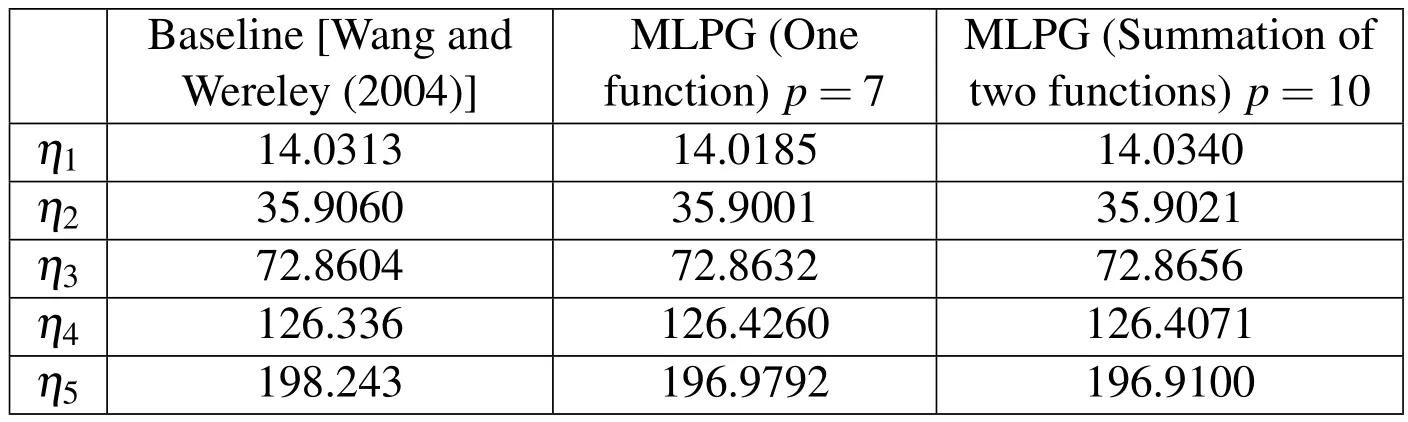
Table 4:Natural frequencies of a non-uniform beam for non-dimensional rotating speed s=12.

Figure 7:Mode shapes of a non-uniform beam for rotating speed s=0 （left）and s=12 （right）.

This type of stiffness and mass distribution is suitable for helicopter rotor blades.Tables5and6show the results of a non-uniform non-rotating（cubic stiffness distribution）and non-uniform rotating （cubic stiffness distribution）beam,respectively.Figures 8（a）and 8（b）show the mode shapes of a non-uniform non-rotating （cubic stiffness distribution）and non-uniform rotating （cubic stiffness distribution）beam,respectively.

Table 5:Natural frequencies of a non-uniform （cubic stiffness distribution）beam for non-dimensional rotating speed s=0.

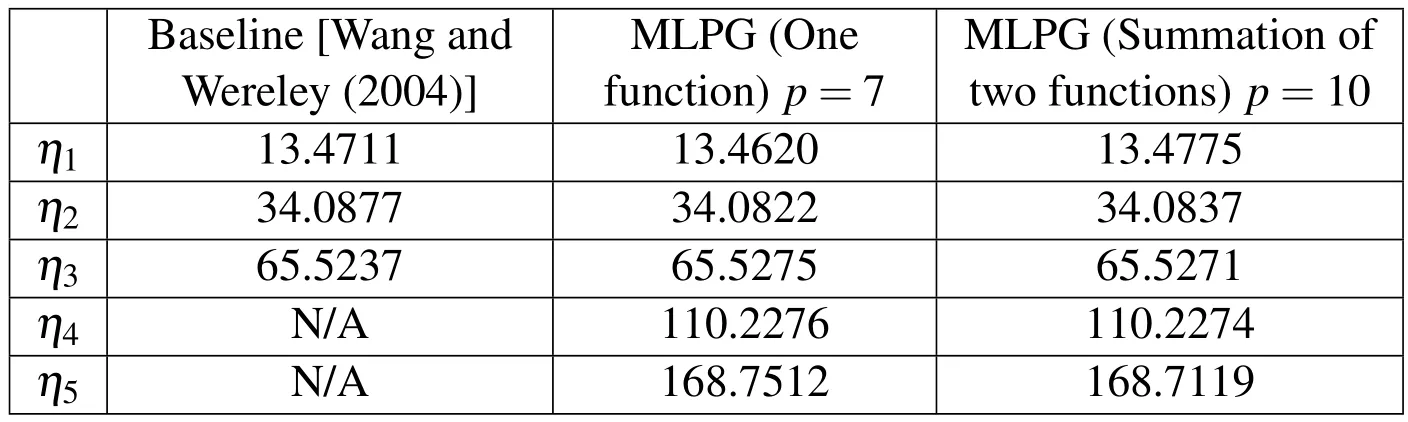
Table 6:Natural frequencies of a non-uniform （cubic stiffness distribution）beam for non-dimensional rotating speed s=12.

7.2 Hinged-Free Boundary Conditions

In references[Bisplinghoff,Ashley,and Halfman （1996）]and[Nagaraj and Shanthakumar（1975）]the problem of hinged-free beam is solved using traditional Galerkin method and Galerkin finite element method,respectively.In traditional Galerkin method,Duncan polynomials are used.In Galerkin finite element method,Hermite polynomial of order 7 is used and only two elements are considered within the domain.In both the cases hinged-free boundary condition with inputused.Table 7 shows the results of a rotating beam.

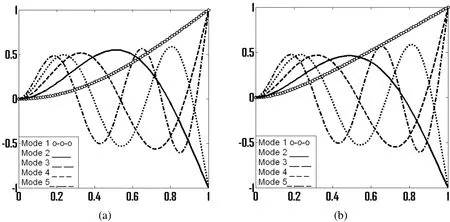
Figure 8:Mode shapes of a non-uniform beam for rotating speed s=0 （left）and s=12 （right）.

Table 7:Natural frequencies of a uniform beam for EI=

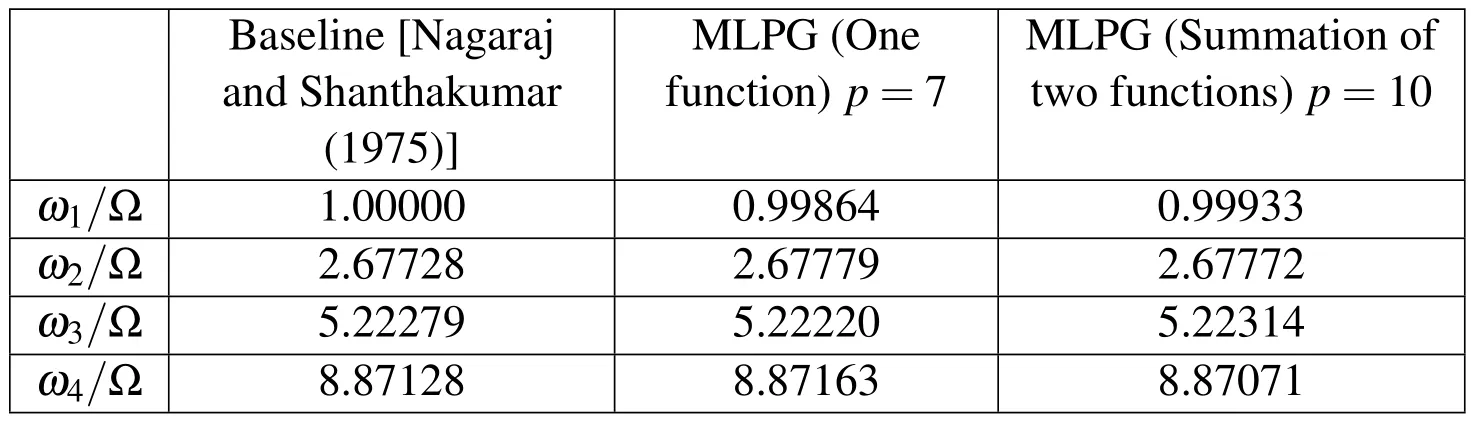
Table 7:Natural frequencies of a uniform beam for EI=

Baseline[Nagaraj and Shanthakumar（1975）]MLPG（One function）p=7 MLPG（Summation of two functions）p=10 ω1/Ω1.00000 0.99864 0.99933 ω2/Ω2.67728 2.67779 2.67772 ω3/Ω5.22279 5.22220 5.22314 ω4/Ω8.87128 8.87163 8.87071

Figure （9）shows the first four mode shapes for the hinged-free boundary condition.Mode shapes show very accurate match with existing literature[Bisplinghoff,Ashley,and Halfman （1996）;Nagaraj and Shanthakumar（1975）].

8 Conclusion

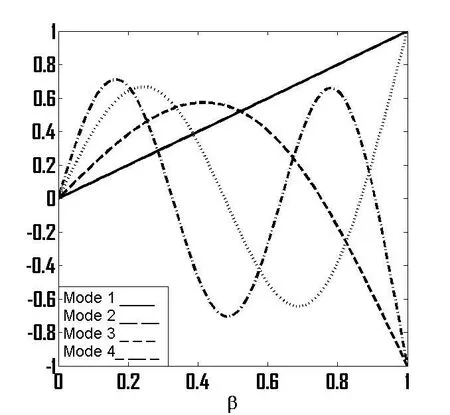
Figure 9:Mode shapes of a uniform rotating beam.

A meshless local Petrov-Galerkin method is successfully used to obtain the free vibration results for a rotating Euler-Bernoulli beam.Radial basis function makes it simpler to apply the essential boundary conditions and computational efforts can be reduced.Summation of two radial basis function is used as well,which shows notable improvements over the radial basis function approximation for one dimensional case:（1）Number of nodes within the sub-domain of the trial function can be increased and （2）higher natural frequencies can be computed with one sub-domain of the trial function.For overlapping domains,the approximation function can be improved further.Results are found to be quite accurate with both approximations.Several cases of polynomial mass and stiffness distribution which can model helicopter and wind turbine blades are explored.It is found that the MLPG method performs very well for these problems.This paper will motivate the application of MLPG method for rotating beam problems which are important in engineering.

Atluri,S.N.（2004）:The Meshless Method（MLPG）for Domain and BIE Discretizations.Tech Science Press,Forsyth.

Atluri,S.N.;Cho,J.Y.;Kim,H.-G.（1999）:Analysis of the beams,using the meshless local Petrov-Galerkin method,with generalized moving least squares interpolations.Computational Mechanics,vol.24,pp.334-347.

Atluri,S.N.;Liu,H.T.;Han,Z.D.（2006）:Meshless local Petrov-Galerkin mixed collocation method for elasticity problems.Computer Modeling in Engineering and Sciences,vol.14,pp.141-152.

Atluri,S.N.;Liu,H.T.;Han,Z.D.（2006）:Meshless local Petrov-Galerkin mixed finite difference method for solid mechanics problems.Computer Modeling in Engineering and Sciences,vol.15,pp.1-16.

Atluri,S.N.;Shen,S.（2002）:The Meshless Local Petrov-Galerkin Method.Tech Science Press,Forsyth,GA.

Andreaus,U.;Batra,R.C.;Porfiri,M.（2005）:Vibration of cracked Euler-Bernoulli beams using meshless local Petrov-Galekin method.Computer Modeling in Engineering and Sciences,vol.9,pp.111-131.

Banerjee,J.R.（2000）:Free vibration of centrifugally stiffened uniform and tapered beams using the dynamic stiffness method.Journal of Sound and Vibration,vol.233,pp.857-875.

Bauchau,O.A.;Hong,C.-H.（1987）:Finite element approach to rotor blade modeling.Journal of the American Helicopter Society,vol.32,pp.60-67.

Belinha,J.（2014）:Meshless Methods in Biomechanics-Bone Tissue Remodeling Analysis.Springer,New York.

Belytschko,Y.;Lu,Y.Y.;Gu,L.（1994）:Element-free Galerkin methods.International Journal for Numerical Methods in Engineering,vol.37,pp.229-256.

Bisplinghoff,R.L.;Ashley,H.;Halfman,R.L.（1996）:Aeroelasticity.Dover Publications,New York.

Bokaian,A.（1990）:Natural Frequencies of beams under tensile axial loads.Journal of Sound and Vibration,vol.142,pp.481-498.

Bramwell,A.R.S.;Done,G.;Balmford,D.（2001）:Bramwell’s Helicopter Dynamics.Bath Press,Oxford.

Chung,J.;Yoo,H.H.（2002）:Dynamic analysis of a rotating cantilever beam by using the finite element method.Journal of Sound and Vibration,vol.249,pp.147-164.

Elgohary,T.A.;Dong,L.;Junkins,J.L.;Atluri,S.N.（2014）:Time domain inverse problems in nonlinear systems using collocation and radial basis functions.Computer Modeling in Engineering and Sciences,vol.100,pp.59-84.

Elgohary,T.A.;Dong,L.;Junkins,J.L.;Atluri,S.N.（2014）:A simple,fast,and accurate time-integrator for strongly nonlinear dynamical systems.Computer Modeling in Engineering and Sciences,vol.100,pp.249-275.

Elgohary,T.A.;Junkins,J.L.;Atluri,S.N.（2015）:An RBF-collocation algorithm for orbit propagation.Advances in Astronautical Sciences,15-359.

Giurgiutiu,V.;Stafford,R.O.（1977）:Semi-analytical methods for frequencies and mode shapes of rotor blades.Vertica,vol.1,pp.291-306.

Gu,Y.T.;Liu,G.R.（2001）:A local point interpolation method for static and dynamic analysis of thin beams.Comput.Methods Appl.Mech.Engrg,vol.190,pp.5515-5528.

Gunda,J.B.;Ganguli,R.（2007）:Stiff-string basis functions for vibration analysis of high speed rotating beams.Journal of Applied Mechanics,vol.75,pp.0245021-25.

Gunda,J.B.;Gupta,R.K.;Ganguli,R.（2008）:Hybrid stiff-string-polynomial basis functions for vibration analysis of high speed rotating beams.Computers and Structures,vol.87,pp.254-265.

Hoa,S.V.（1979）:Vibration of a rotating beam with tip mass.Journal of Sound and Vibration,vol.67,pp.369-381.

Hodges,H.D.;Rutkowski,M.J.（1981）:Free-vibration analysis of rotating beams by a variable-order finite element method.AIAA Journal,vol.19,pp.1459-1466.

Hu,D.;Wang,Y.;Li,Y.;Gu,Y.;Han,X.（2014）:A meshfree-based local Galerkin method with condensation of degree of freedom.Finite Elements in Analysis and Design,vol.78,pp.15-24.

Johnson,W.（1980）:Helicopter Theory.Dover Publications,New York.

Liu,G.R.（2003）:Meshfree Methods.CRC Press,New York.

Long,S.;Atluri,S.N.（2002）:A meshless local Petrov-Galerkin method for solving the bending problem of a thin plate.Computer Modeling in Engineering and Sciences,vol.3,pp.53-63.

Most,T.;Bucher,C.（2005）:A moving least squares weighting function for the Element-free Galerkin method which almost fulfills essential boundary conditions.Structural Engineering and Mechanics,vol.21,pp.315-332.

Nagaraj,V.T.;Shanthakumar,P.（1975）:Rotor blade vibration by the Galerkin finite element method.Journal of Sound and Vibration,vol.43,pp.575-577.

Nayroles,B.;Touzot,G.;Villon,P.（1992）:Generalizing the finite element method:Diffuse approximation and diffuse elements.Computational Mechanics,vol.10,pp.307-318.

Putter,S.;Manor,H.（1978）:Natural frequencies of radial rotating beams.Journal of Sound and Vibration,vol.56,pp.175-185.

Raju,I.S.;Phillips,D.R.;Krishnamurthy,T.（2004）:A radial basis function approach in the meshless local Petrov-Galerkin method for Euler-Bernoulli beam problems.Computational Mechanics,vol.34,pp.464-474.

Sladek,J.;Stanak,P.;Han,Z-D.;Sladek,V.;Atluri,S.N.（2013）:Applications of the MLPG method in engineering and sciences:A review.Computer Modeling in Engineering and Sciences,vol.92,pp.423-475.

Sushma,D.;Ganguli,R.（2012）:A collocation approach for finite element basis functions for Euler-Bernoulli beams undergoing rotations and transverse bending vibration.International Journal for Computational Methods in Engineering Science and Mechanics,vol.13,pp.290-307.

Tian,J.;Rao,S.S.（2012）:Meshless local Petrov-Galerkin method for threedimensional heat transfer analysis.Journal of Heat Transfer,vol.134,pp.112701-9.

Vinod,K.G.;Gopalakrishnan,S;Ganguli,R.（2007）:Free vibration and wave propagation analysis of uniform and tapered rotating beams using spectrally formulated finite elements.International Journal of Solids and Structures,vol.44,pp.5875-5893.

Wang,G.;Wereley,N.M.（2004）:Free vibration analysis of rotating blades with uniform tapers.AIAA Journal,vol.42,pp.2429-2437.

Wright,A.D.;Smith,C.E.;Thresher,R.W.;Wang,J.L.C.（1982）:Vibration modes of centrifugally stiffened beam.Journal of Applied Mechanics,vol.49,pp.197-202.

Zhang,J.（2001）:Active-passive hybrid optimization of rotor blades with trailing edge flaps.Ph.D.thesis,Pennsylvania State University.

1Ph.D.Student,Department of Aerospace Engineering,Indian Institute of Science,Bangalore,India.E-mail address-vijaypanchore@aero.iisc.ernet.in

2Professor,Department of Aerospace Engineering,Indian Institute of Science,Bangalore,India.E-mail address-ganguli@aero.iisc.ernet.in

3Chief Research Scientist,Department of Aerospace Engineering,Indian Institute of Science,Bangalore,India.E-mail address-omkar@aero.iisc.ernet.in