应用多重分形法确定老挝窑房地区水系沉积物异常下限

刘小春，李 俊，陈 希，赵春丽，李 昊

（云南省地质矿产勘查院，昆明 650051）

0 引言

成矿过程是在特定的地球化学场中发生、演化和发展，因此在成矿预测中确定地球化学异常下限显得尤为重要。过去确定地球化学异常下限往往采用经典的统计学方法，认为地球化学元素在场中的分布满足正态分布或对数正态分布。但有研究资料表明，地球化学景观的形成经历了复杂的历史演化，元素曾发生过不同尺度的迁移和富集［1］；地球化学元素分布具有标度不变性或自相似性，服从分形分布，可以用分形来刻画元素在场中的变化和特征。同时，地球化学元素亦具有空间结构性和层次性。成秋明等［2－3］提出用多重分形理论来分离地球化学背景值与异常，而且能够有效地度量场的局部奇异性，不会造成数据信息元的丢失。本文将采用多重含量－求和法计算老挝丰沙里省窑房地区水系沉积物中Au，Cu，Pb，Zn元素的异常下限，利用异常下限编制地球化学元素异常等值线图，以期为区内下一步的找矿工作提供找矿信息。

1 地质概况

老挝丰沙里省窑房地区属于思茅—大叻微陆块的思茅—彭世洛—大叻中－新生代盆地构造带（即思茅—彭世洛—大叻中铜铅锌多金属矿成矿带）的中段。区内中生代地层发育，为一套海陆交替相的红色沉积建造。上二叠统（P2）：岩性主要为灰岩、燧石、砂岩、页岩。上三叠统（T3）：岩性主要为海相砂岩、凝灰质砂岩、灰岩、砾岩。中－下侏罗统（J1－2）：岩性主要为海相砂岩、粉砂岩、钙质页岩，向上逐渐变为陆相页岩，呈 NW－SN 向展布。上－中侏罗统（J2－3）：岩性主要为粉砂岩、泥岩，受断层构造控制，近NW向展布。下白垩统（K1）：岩性为砂岩、泥岩，呈NE－SN向展布。上白垩统（K2）：岩性为碎屑岩含岩盐、芒硝，NE向展布，局部呈大透镜状覆盖下白垩统。此外，局部有新近系（N）出露，岩性为砂砾岩、粉砂岩、黏土岩夹褐煤（图1）。区内地质构造较为简单，为一单斜构造，地层总体走向近SN，倾向W；断裂构造主要呈NE向和NNW向展布。区内岩浆岩主要为白垩纪火山岩，以基性为主，主要岩性为凝灰岩等。区内发育矿产以铜、金、铅锌为主。

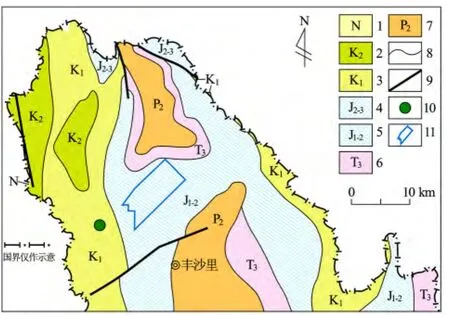
图1 窑房地区区域地质简图Fig.1 Sketch of regional geology in Yaofang area，Phongsaly Province，Laos

2 地球化学异常下限的确定

2.1 传统的统计学方法

如果数据满足正态分布或对数正态分布，一般是以数据的平均值与n倍标准差σ之和＋nσ作为地球化学异常的下限。通常情况采用＋2σ作为异常下限值，根据具体情况也有采用＋1.5σ或＋3σ作为异常下限值。如果数据不满足正态分布或对数正态分布，则需要计算全区各元素原始数据的均值和标准差σ；按＋3σ的条件剔除一批高值后获得一个新数据集，再计算此数据集的均值和标准偏差σ；重复第二步，直至无特高值点存在，求出最终数据集的均值X和标准偏差σ，再求取＋3σ作为各元素异常下限值。

2.2 分形模型方法

分形几何的概念在1975年由曼德布罗特提出［1］，描述一切具有自相似性或标度不变性的复杂事物，并且用分维数D来刻画自然现象的不规则程度［4］。对于一个具有维数的几何形状，若用与它维数相同的尺度r去度量，其大小N（r）与线性尺度r存在幂函数关系［5］：

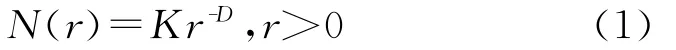
式中，r表示特征尺度；K＞0，是比例常数；D＞0，称为分维数。N（r）＝N（≥r）表示尺度大于等于r的数目或和数。例如：用r表示某元素的含量，N（r）表示元素含量大于等于r的和数［6－9］。

如果元素服从多重分形分布，则存在如下关系［7，10］：

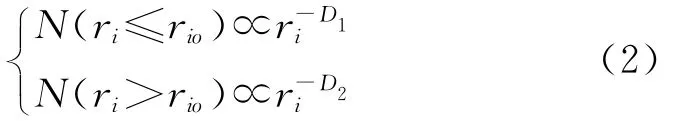
式中，rio表示区域异常下限，元素分布在空间上存在层次性特征，即存在背景分形分布和异常分形分布。

对（2）式加上比例系数K后两，边取对数得到一元线性回归模型：

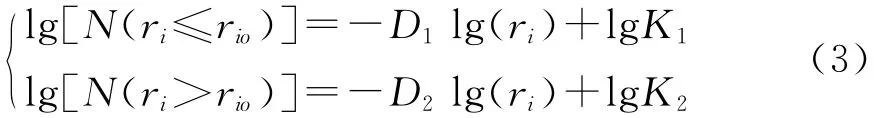
为了求出分维数D1，D2，拟合各分段区间的直线方程确定异常下限rio，引入最小二乘法。即如果给一组定数据点（lgri，lgN（ri）），则寻求拟合直线方程使得差值的平方和E＝Σ［lgN（ri）－（－DlgrilgK）］2为最小［11］，方程直线斜率的估算值即为分维数D。

根据最小二乘法的基本原理，对（3）中的参数求偏导数且令：

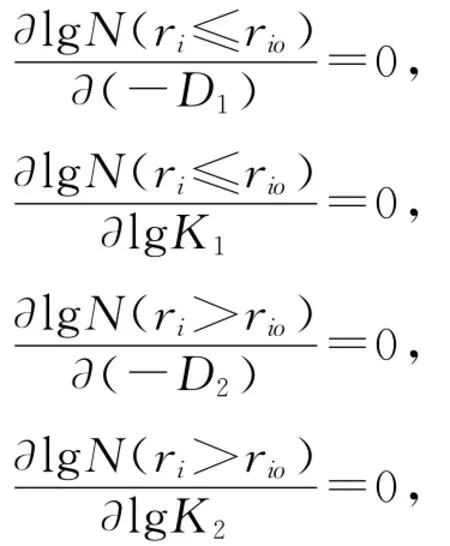
可得：

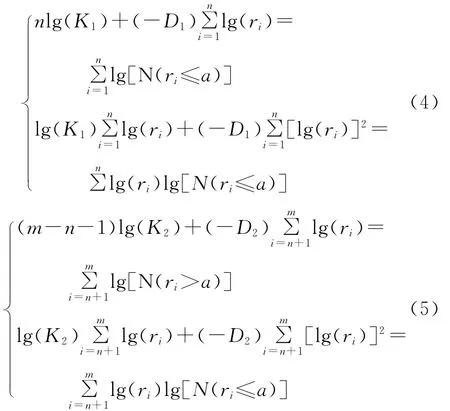
数据点（lg ri，lgN（ri））在lg N（r）—lg r直角坐标系中，大致分布在两段直线上，两段直线的交点对应的lg ri为异常下限rio的对数值。为了提高分界点的客观性，在两个区间段用最小二乘法进行回归时，用最优化方法确定分界点，使区间拟合的直线与原始数据之间的剩余平方和Ei（i＝1，2）在各个区间的总和为最小［5－6，8－9］，即：

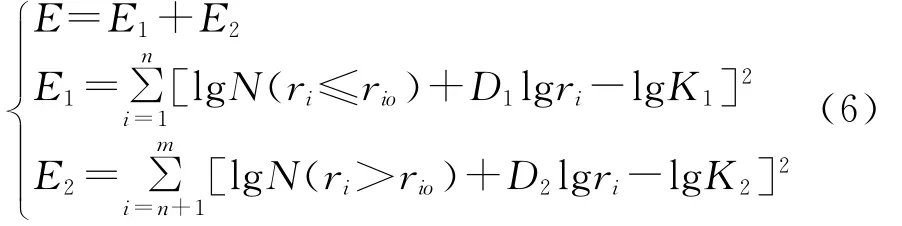
3 应用实例

在本次工作中，1∶5万水系沉积物样品的点位全部分布在侏罗系中－下统中（图2）。

图2 水系沉积物采样位置图Fig.2 Sampling locations of stream sediment

本文采用的样品来自老挝丰沙里省窑房地区1∶5万地球化学水系沉积物测量项目，共计980件，样品全部野外加工。根据地球化学景观与滇西南一带较为相似，不再做粒级实验，直接采用滇西南红层的粒级，≥60目。元素含量测试工作由国土资源部昆明矿产资源监督检测中心分别采用石墨炉原子吸收法（Au）和 X荧光光谱法（Cu，Pb，Zn）完成，所提供的分析数据质量可靠，完全满足计算分形异常下限的需求。

本次工作对样品采用Q—Q图进行统计频率分布特征分析，从Q—Q图可以直观检验元素是否服从正态分布或对数正态分布［12］。根据Q—Q图统计结果（图3）可知，Au，Cu，Pb，Zn元素分布未在或近似在一条直线上，如果利用传统的统计学方法来计算异常下限，必须逐次剔除高值。经处理后得到Au、Cu、Pb、Zn 元素的异常下限分别为 2.75，40.26，29.27，87.57。

采用分形含量－求和法对 Cu，Pb，Zn，Ag，Au，As，Sb元素进行N（r）统计。以Cu为例，其统计结果见表1。

根据含量－求和法统计出各元素的r、N（r）取对数，分别绘制在直角坐标系中（图4），从图中可以看出各元素在空间上至少满足两个层次的分形分布，说明利用分形方法求取该区异常下限是有效的。

为了计算各元素的分维数及拟合直线各分段区间的剩余平方和，以Cu为例应用表1中的数据进行分形统计，结果见表2所述。

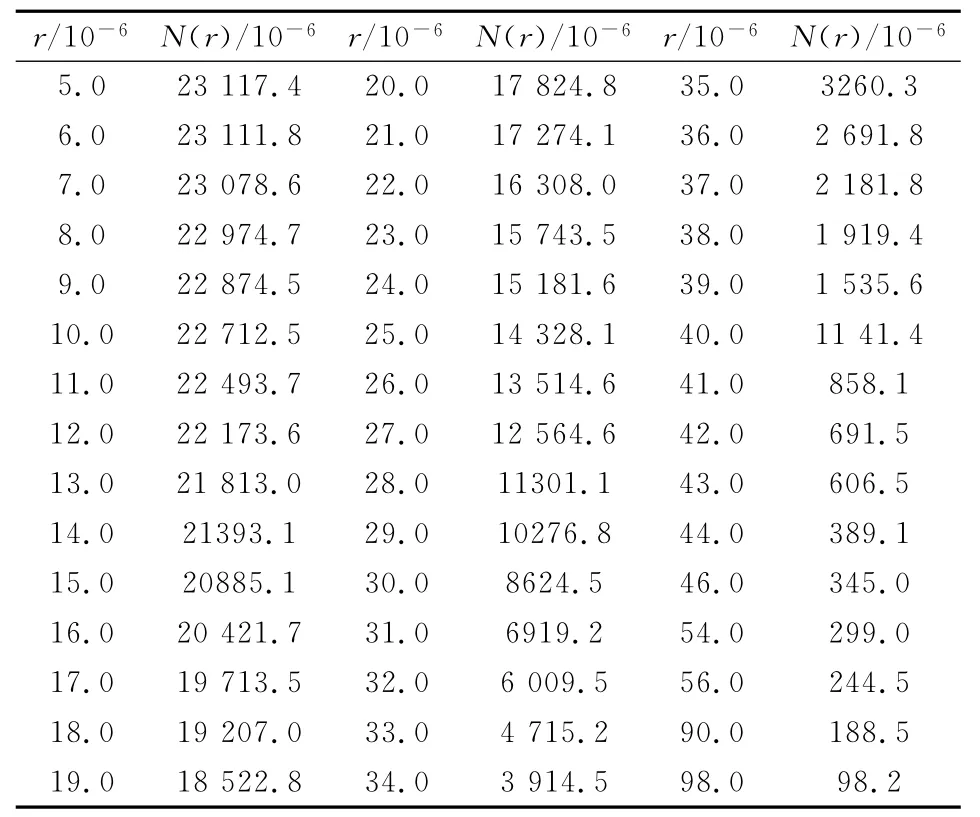
表1 铜元素含量－求和法求出的N（r）结果统计表Table 1 Statistics of N（r）results of Cu obtained by content－summation method

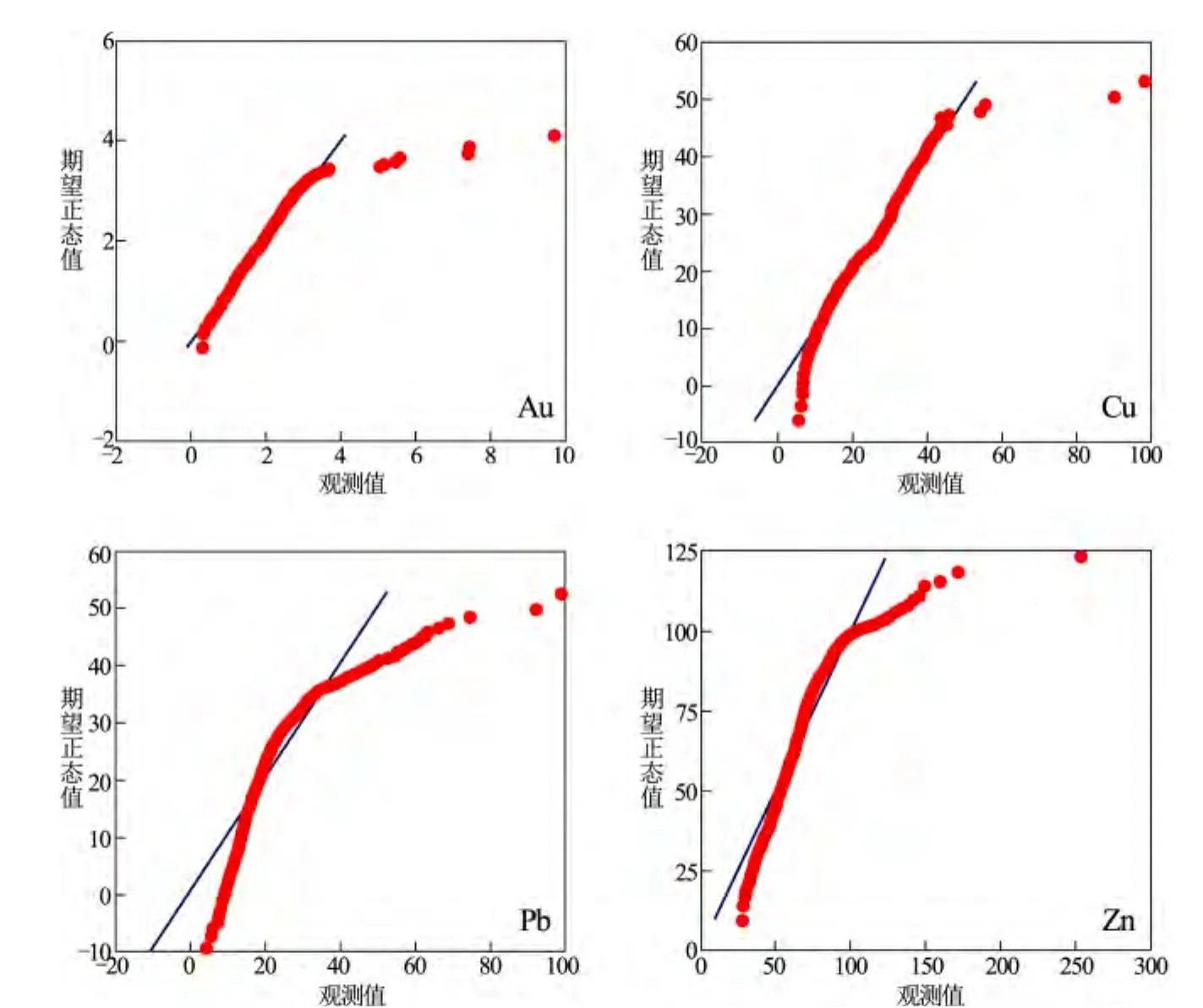
图3 金铜铅锌元素含量的统计分析Q—Q图Fig.3 Q—Q diagram of statistical analysis analysis of Au，Cu，Pb and Zn contents

从表2中不难看出：

当n＝19，两段区间的剩余平方和E1＋E2为0.003最小，即lgrio＝1.354时，rio＝22.6为铜元素的异常下限。得到的拟合直线方程为：

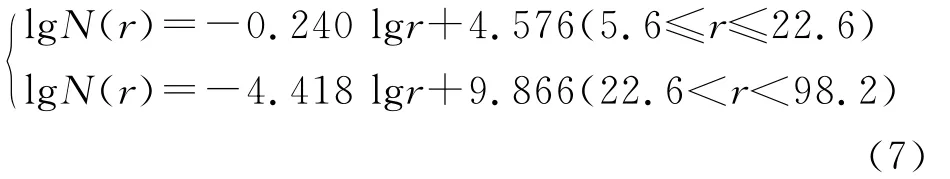
相应的分维数D1＝0.240，D2＝4.148，且两个方程皆通过了回归结果的检验。

同理，当n＝12，15，29，两端区间的剩余平方和E1＋E2为0.002，0.028，0.001最小，即lgrio＝0.128，1.287，1.748时，rio＝1.34，19.35，56分别为 Au，Pb，Zn元素的异常下限。得到的拟合直线方程为：相应的分维数 D1＝0.195，0.164，0.248；D2＝2.655，2.906，4.124，且6个方程皆通过了回归结果的检验。

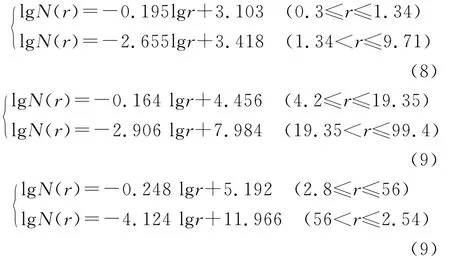
4 应用效果

将两种方法求得的异常下限对比，分形方法求得异常下限低于传统方法，在文献［7］中也得出类似的结论。图5和图6分别为两种不同异常下限圈定的Au，Cu，Pb，Zn元素地球化学异常等值线图。

从图5，图6可以看出，分形含量－求和法确定的异常下限圈定的异常范围较大、较连续，利于圈定隐伏、半隐伏矿体形成的弱异常；而统计方法确定的异常下限圈定的异常孤立，各个孤立异常范围之间很有可能难以找到线性关系，不易确定矿化信息的总体走向。

综上所述，各种地质成矿过程是在一定地球化学场中进行的，不同的地球化学场的分布模式可能会得出不同的地质成矿时空演化过程，在这个演化过程中各种地球化学流体中的元素萃取、迁移、富集以及热力学方式的准确界定有利开展化探找矿工作，所以元素地球化学场分布的确定尤其重要。新的研究表明元素在地球化学场的分布极少满足正态分布或对数分布，元素的分布服从标度不变性或自相似性，地球化学景观可能是一个具有低维（D＝2.9）吸引的混沌系统，具有典型的分形特征［13］。因此，本次工作采用分形方法来确定异常下限更符合地球化学本质特征，能有效地刻画元素分布机制，反映出元素异常分布范围。

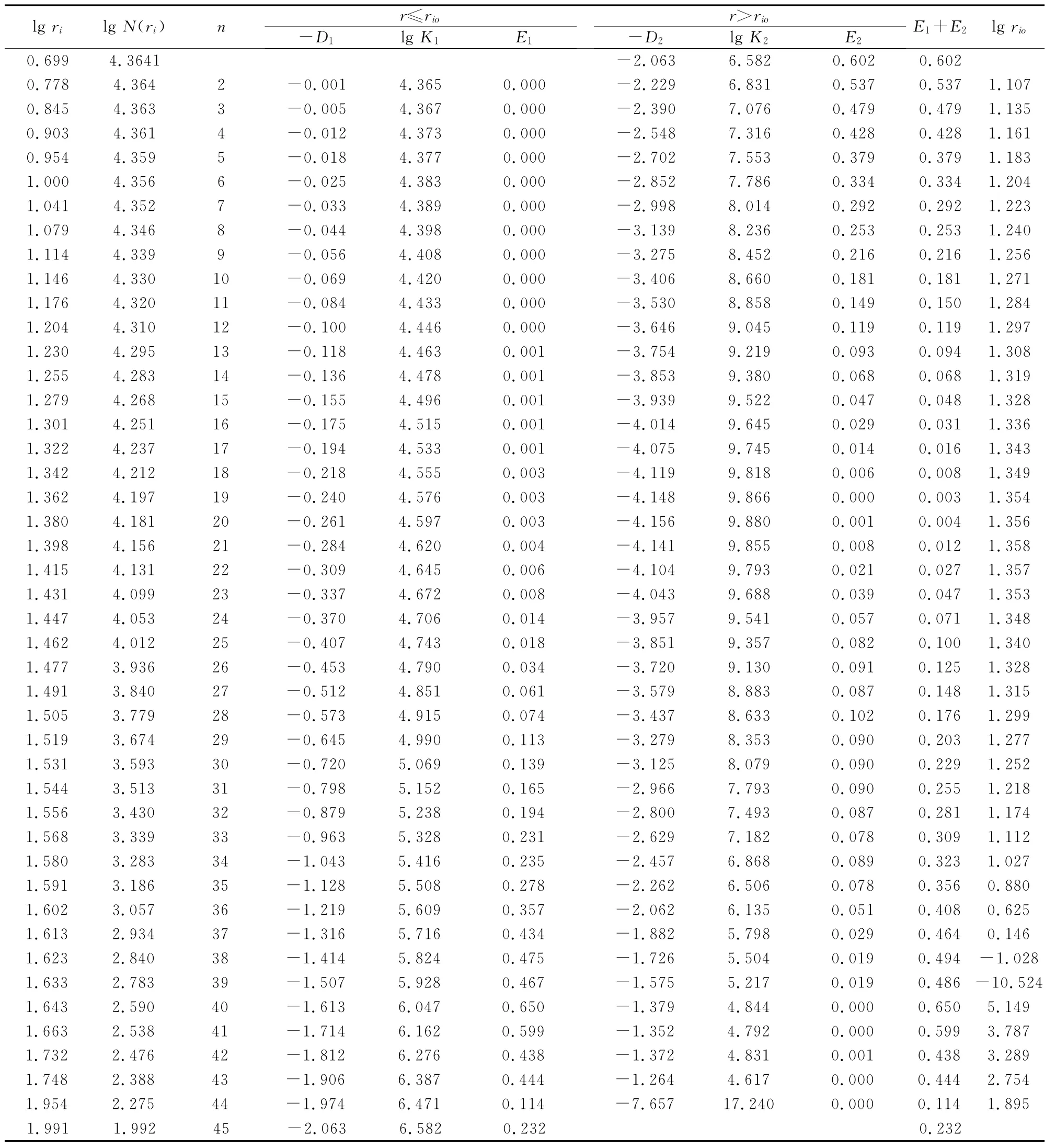
表2 铜元素的分维数计算结果表Table 2 Computing results D of Cu

5 结论

（1）老挝丰沙里省窑房地区发育有大量的二叠系红层建造，其矿化元素含量值不高，矿化蚀变信息较弱，利用分形下限圈定地球化学异常更能突显一定区内的找矿信息，与地球化学水系沉积物测量找矿的思想是吻合的。

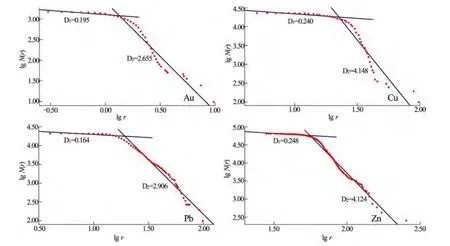
图4 Au，Cu，Pb，Zn元素lg N（r）—lg r及最小二乘法拟合图Fig.4 Diagram showing lg N（r）—lg r of Au，Cu，Pb and Zn fitting of least squares method

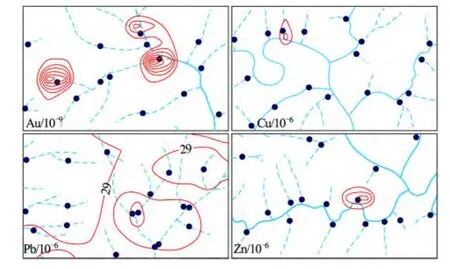
图5 统计法异常下限圈定的异常等值线Fig.5 Contour of statistical threshold

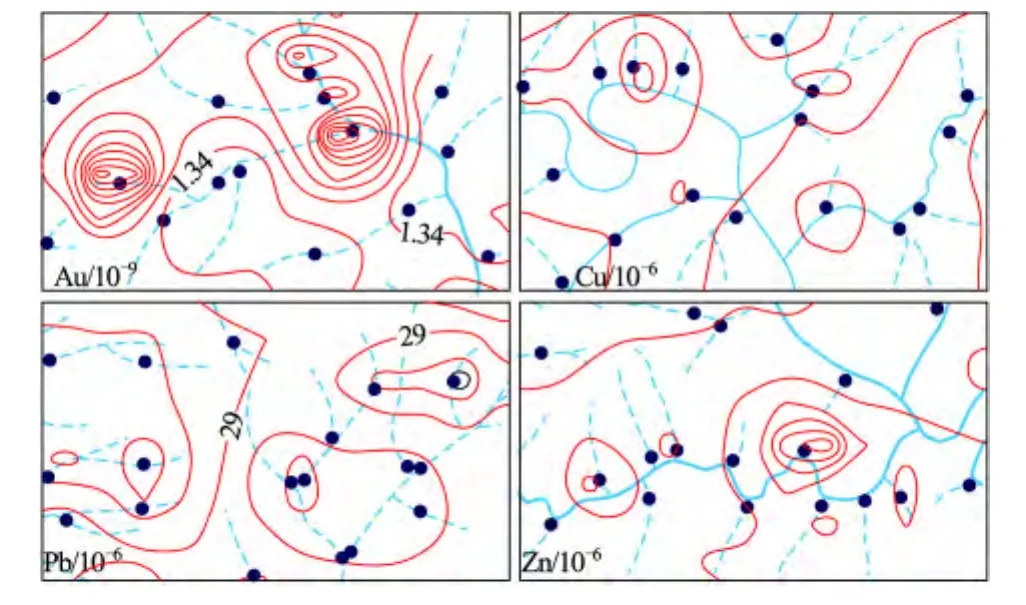
图6 分形法异常下限圈定的异常等值线Fig.6 Contour of fractal threshold

（2）Au与Pb，Cu与Zn在各层次上的分维数相近，但后者的分维数大于前者，说明在区域上Cu，Zn元素的地球化学过程更强烈，亦或有后期的含Cu，Zn流体的混入叠加。

（3）根据分形理论，元素的分布至少满足两个层次的分形分布，低分维的分形分布描述地球化学背景场，高分维的分形分布刻画地球化学异常场。

（4）与多重含量－频数、多重含量－面积、多重含量－距离、多重含量－周长等分形方法相比，多重含量－求和法更易理解、计算，在地质生产单位更易推广，能很好的为地质找矿服务。

［1］申维.分形混沌与矿产预测［M］.北京：地质出版社，2002：1－131.

［2］Cheng Qiuming，Agterberg F P，Ballantyne S B.The separation of geochemical anomalies from background by fractal methods［J］.Journal of Geochemical Exploration，1994，51：109－130.

［3］成秋明.多重分形与地质统计学方法用于勘查地球化学异常空间结构和奇异性分析［J］.地球科学，2001，26（2）：161－166.

［4］张济忠.分形［M］.北京：清华大学出版社，2004：1－436.

［5］井国正，闫杰，文雪峰，等.分形理论在江日呷玛地区地球化学异常圈定中的应用［J］.矿产勘查，2010，1（4）：375－379.

［6］李随民，姚书振.基于MAPGIS的分形方法确定化探异常［J］.地球学报，2005，26（2）：187－190.

［7］孙忠军.矿产勘查中化探异常下限的多重分形计算方法［J］.物探化探计算技术，2007，29（1）：54－57.

［8］张磊，申维.分形方法在澳大利亚新南威尔士地区地球化学异常下限确定中的应用［J］.地质通报，2009，28（2－3）：245－249.

［9］胡青华，肖晓林，曹圣华，等.地球化学异常下限的含量－面积分形计算方法——以江西永平地区为例［J］.东华理工大学学报（自然科学版），2011，34（2）：107－110.

［10］孙忠军.矿产资源潜力地球化学定量预测新理论新方法［D］.北京：中国地质大学（北京），2003.

［11］韩庆瑶，肖强，乐英.空间离散点最小二乘法分段直线拟合的研究［J］.工业仪表与自动化装置，2012（4）：107－109.

［12］张焱，周永章，黄锐，等.粤北刘家山地区多元素分形维数谱函数及其对矿化的指示分析［J］.中山大学学报（自然科学版），2012，51（2）：119－124.

［13］李长江.矿产勘查中的分形、混沌与ANN［M］.北京：地质出版社，1999：1－140.