基于速度－状态摩擦本构定律的三维DDA方法

张龙，江在森，武艳强，2＊，邹镇宇，3，刘晓霞，3，魏文薪

1中国地震局地震预测研究所地震预测重点实验室，北京 100036

2中国地震局第一监测中心，天津 300180

3中国地震局地质研究所地震动力学国家重点实验室，北京 100029

1 引言

非连续变形分析（DDA）方法是岩土工程领域模拟节理岩体运动与变形的一种数值解析方法（Shi，1992）.该方法将不连续面分割的岩体视为块体集合，以最小势能法建立总体平衡方程，利用单纯形积分与开闭迭代方法保证结果的精确性与计算的高效性，最终求得各块体的位移与变形（Shi，2001；Wu et al.，2012）.DDA方法因收敛速度高以及模拟结果精确等优势，广泛应用于边坡破坏（Sitar et al.，2005；Wu，2010；Wu and Chen，2011）、洞室开挖（邬爱清等，2006；Law and Lam，2003）以及爆破（刘刚等，2003）等动力学模拟研究中.此外，DDA方法在模拟区域地壳变形与应变积累领域也得到了初步应用（陈兵等，2000；陈祖安等，2008；秦小军等，2001；王辉等，2003；Liu et al.，1996）.

DDA方法中块体单元之间的接触界面是位移间断面，界面滑动与否由Mohr－Coulomb准则控制，当剪应力τ满足公式（1）时，接触状态由锁定变为摩擦滑动.

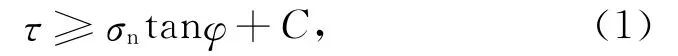
式中σn为接触边界上的正应力，φ和C分别是摩擦角和黏着力（Shi，1992，2001），摩擦系数μ（＝tanφ）在模拟过程中保持不变.由于岩土工程主要针对水坝、边坡等百米尺度、岩性相对均一的研究目标，采用常摩擦系数进行数值模拟已足够精确.然而，针对更大尺度的地学问题，实验室测量与野外调查结果均表明，地震成核、震前滑动、同震破裂、余震和震后余滑以及震间期断层的愈合过程中，断层面的摩擦系数并非常数（Marone，1998）.因此，为合理解释地震周期各阶段发震断层行为及剪应力变化过程，需要在数值模拟时采用更符合实际的摩擦本构定律（张龙等，2013）.

基于实验室摩擦实验结果得到的速度－状态摩擦本构定律能够模拟断层面上的成核过程以及发生在俯冲带的周期性慢滑移，结合数值模拟方法还可直观给出地震周期的轮廓 （Lapusta and Rice，2003；Liu and Rice，2007）.该定律中，断层面的摩擦强度由滑动速度V和状态变量θ共同描述，其基本形式如下（Dieterich，1979，1981；Ruina，1983）：

为了实现复杂介质的地震孕育、发生及震后调整全过程的数值模拟研究，首先需要解决速度－状态摩擦本构定律与动力学数值模拟方法的融合问题.本文选择三维DDA方法作为研究对象，首先推导了基于速度－状态摩擦本构定律的三维DDA模拟实用公式，随后设计了滑动－保持－滑动实验和速度步进实验两算例以验证模拟效果，并分析了数值模拟结果与实验室摩擦实验结果存在细微差别可能的原因.

2 计算方法

由公式（2）和公式（3）知，块体接触面上每一时间步的摩擦系数μ由当前时步的速度V和状态变量θ共同决定，其他参数（μ0，V0，Dc，a和b）均为常数.下面详细推导了改进的三维DDA算法中计算摩擦系数的实用公式.

2.1 速度

应用三维DDA方法求解块体速度时，选择动力学计算模式，即每一时步结束时的速度为下一时步开始时的速度.D＝ （uvwrxryrzεxεyεzγxyγyz γzx）T表示块体变形量，包含块体位移、旋转和应变.令Δt为时步长，Di和Di＋1为t和t＋Δt时刻的块体变形量，采用向前差分格式（Shi，1992，2001），则有

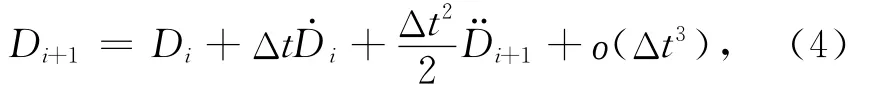
在小步长情况下可假定每一时步内的加速度为常数，即

令当前时步初始变形量为0，即Di＝0，公式（4）略去高阶无穷小并代入公式（5）得

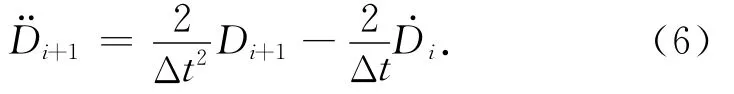
匀加速直线运动速度计算表达式为

部分公民环保意识薄弱，碳信息披露可以促进企业可持续发展，但企业对此认识不够深刻，这些都使碳披露难以发挥其对经营管理的指导作用。这就需要社会广泛宣传低碳经济理念，提高公民的环保意识，进而逐步上升到企业管理层面，使管理者提高环保责任意识，加大对碳信息的重视。通过学习，掌握必要的碳披露知识，推动经济社会可持续发展。

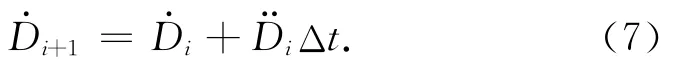
将公式（6）代入公式（7），整理得速度迭代表达式

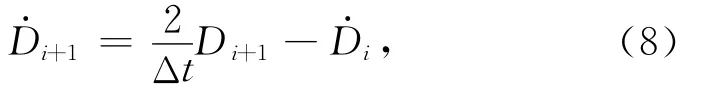
令Vi和Vi＋1分别表示，则（8）式可表示为

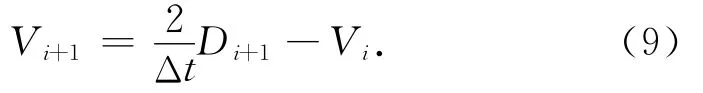
2.2 状态变量

根据公式（2）或（3）的演化方程计算得到状态变量θ.以公式（2）为例，将演化方程用4阶Runge－Kutta方法离散，即

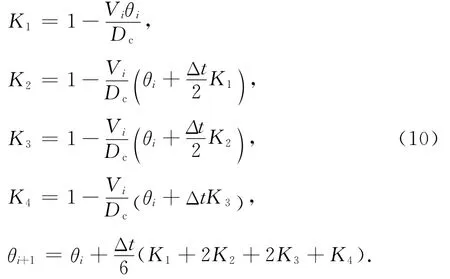
式中θi和θi＋1分别为t和t＋Δt时刻的状态变量，Kj（j＝1，2，3，4）为中间变量.初始时刻的θ值由公式（2）（或（3））的主方程求得.

根据公式（9）和（10）分别计算得到下一时步的速度V和状态变量θ，代入公式（2）（或（3））可计算得到下一时步的摩擦系数μ，完成该时间步计算.将上述算法嵌入三维DDA程序中，建立了应用速度－状态摩擦本构定律的三维DDA方法.

3 数值模拟

为验证结合速度－状态摩擦本构定律的三维DDA方法在计算地震周期中断层行为问题时的精确性，本文设计了滑动－保持－滑动实验和速度步进实验两个算例.

3.1 滑动－保持－滑动实验

研究表明，相比于其他形式的本构定律，Dieterich law能够准确描述应力降与保持时间的关系，即静摩擦的时间依赖性（Dieterich，1978）.最初，实验室做滑动－保持－滑动实验使用“三明治”直剪实验机（图1a），Scholz（2002）将其简化为图1b形式.

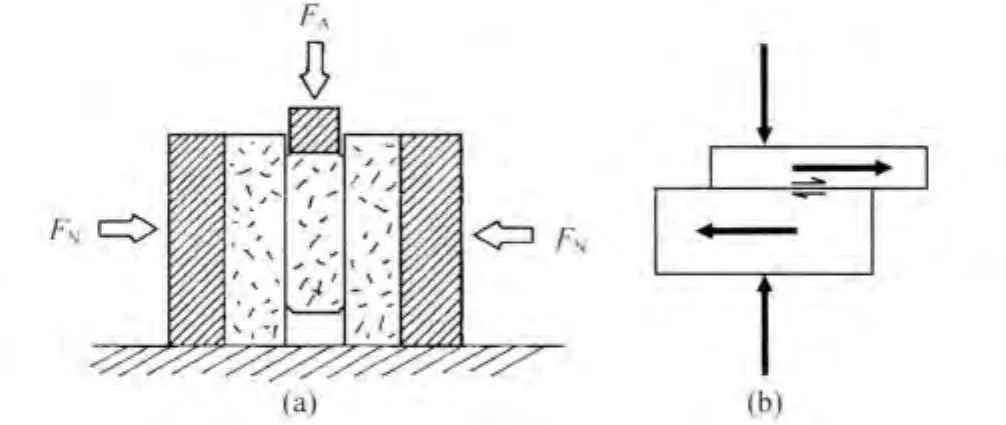
图1 （a）“三明治”直接剪切实验机；（b）Scholz简化的直接剪切实验机Fig.1 （a）Schematic diagram of“sandwich”direct shear apparatus；（b）Direct shear apparatus modifid by Scholz

利用改进的三维DDA方法数值模拟该实验，需要设计形状合适的模型并合理选择材料的物理参数.考虑到摩擦强度变化与接触面积大小无关，为简化模拟，对模型几何形状略作修改，如图2所示.模型的介质参数、数值控制参数及摩擦本构参数见表1.

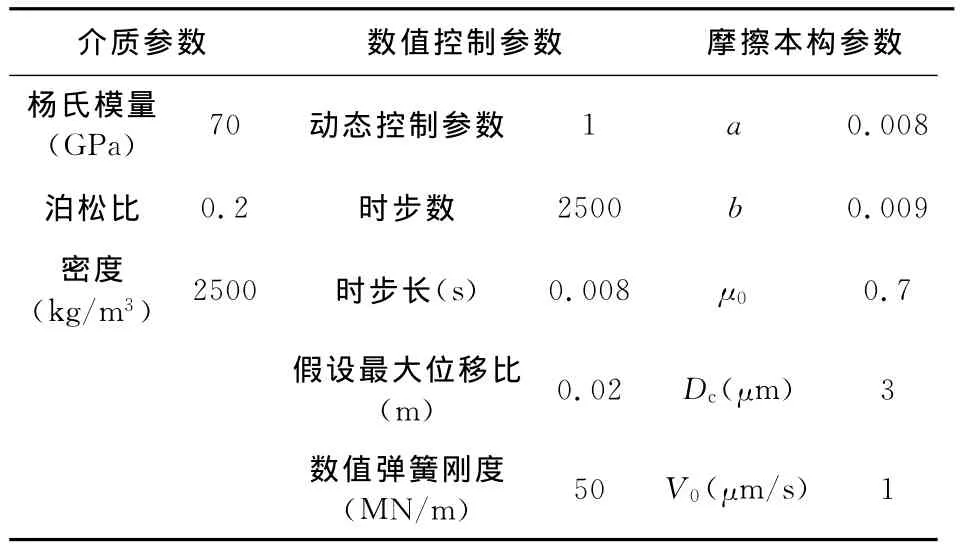
表1 滑动－保持－滑动实验数值参数表Table 1 Numerical parameters of slide－hold－slide tests for 3DDDA forward modeling simulation

为与实验室摩擦实验数据（Beeler et al.，1994）进行对比，本文分别做了保持时间为1s、10s、100s、1000s和10000s的滑动－保持－滑动数值实验.限于篇幅，仅以图3为例给出保持时间为10s的滑动－保持－滑动数值实验模拟结果.

图2 滑动－保持－滑动实验的模型几何Fig.2 Numerical model for slide－hold－slide tests

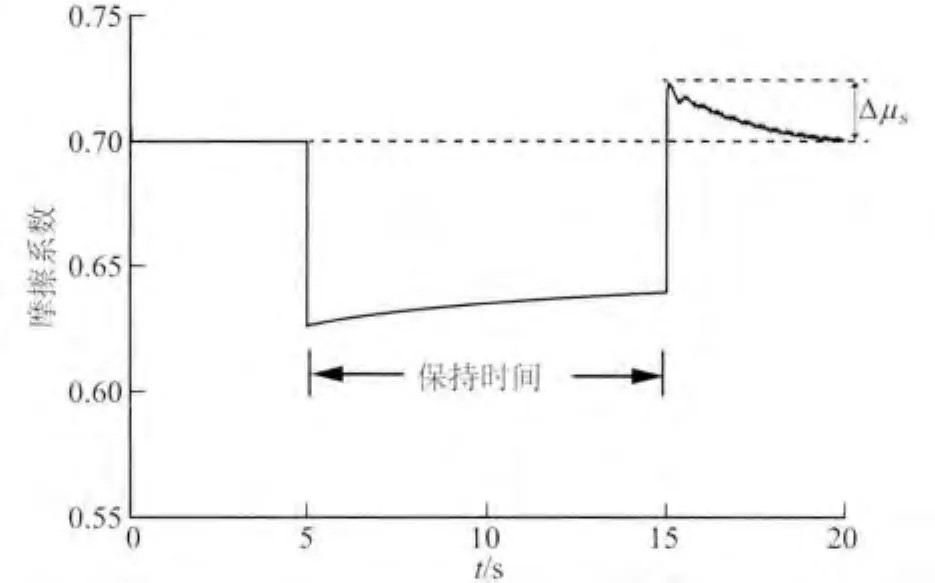
图3 滑动－保持－滑动数值实验模拟结果（保持时间为10s）Fig.3 Numerical results of slide－hold－slide tests（hold period is 10s）

如图3所示，前5s滑块在荷载力和摩擦力的共同作用下做匀速直线运动，即“滑动”过程；5～15s为“保持”阶段，即令荷载速度为零，滑块在摩擦力的作用下做减速运动，此时摩擦系数也发生相应变化；15～20s仍为“滑动”阶段，15s时重载初始时刻荷载速度，可明显观察到静摩擦系数瞬间达到峰值，随着时间的增加不断减小，最终恢复到初始水平.不同保持时长的滑动－保持－滑动数值实验摩擦系数演化过程与该结果类似.

图4给出了静摩擦变化量Δμs（峰值摩擦系数与稳态值的差值）与保持时间的关系.实验室摩擦实验结果与地震学对断层愈合速率的估计均表明，准静态接触时摩擦愈合量Δμs与保持时间的对数呈线性关系（Beeler et al.，1994），即所谓静摩擦时间依赖性.图4表明，模拟结果与实验室测量结果（Beeler et al.，1994）基本吻合.当保持时间为101～104s时，模拟数据与实验数据对数拟合后呈线性变化且斜率相同，拟合优度均为0.999，将两部分数据混合再进行对数拟合的拟合优度依然高达0.997.由此得出结论，应用速度－状态摩擦本构定律的三维DDA方法能够比较准确地描述静摩擦的时间依赖性.另外，摩擦愈合速率β（＝Δμs每十年的变化量）.在速度接近零时可由摩擦本构参数b衡量（Beeler et al.，1994）.换言之，用该方法可求出Dieterich law中本构参数b.图4中保持时间为101～104s的数值模拟结果斜率为0.00856，与摩擦本构参数b（＝0.009）十分接近，相对误差约为5%，表明应用速度－状态摩擦本构定律的三维DDA方法进行数值模拟可以基本满足精度要求.

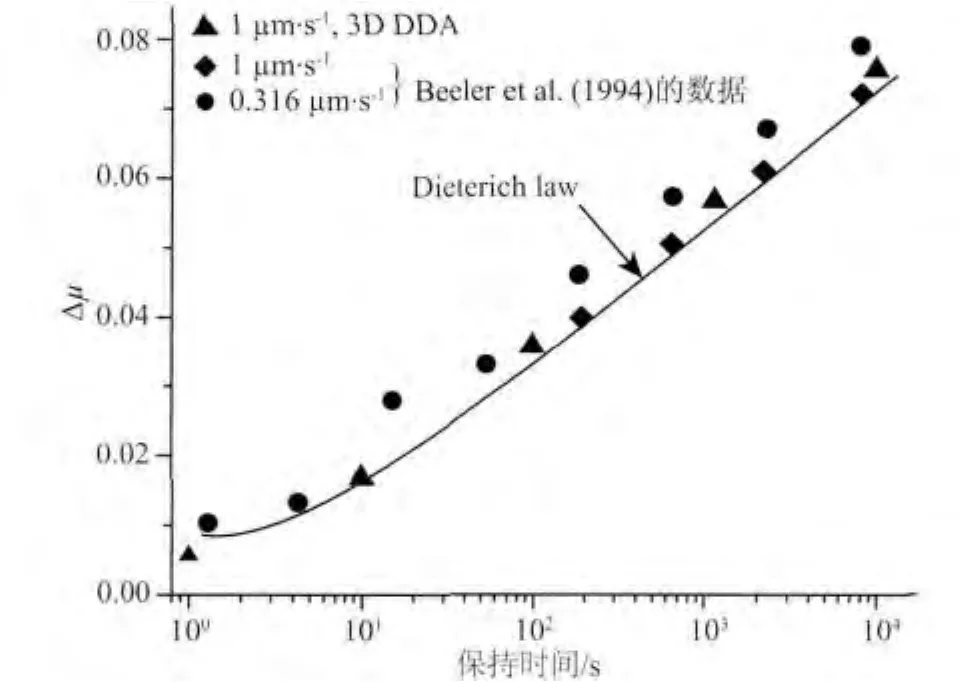
图4 滑动－保持－滑动实验的数值结果与实验室结果图中三角形表示三维DDA的数值实验结果，圆点和菱形表示Beeler等（1994）实验室摩擦实验结果.实线代表用Dieterich law对滑动－保持－滑动实验数值模拟的结果.Fig.4 Comparison between numerical results and laboratory measurements for slide－hold－slide tests In this figure，numerical results performed by 3DDDA are showed as triangles.Circles and diamonds represent the laboratory data measured by Beeler et al.（1994）.The curve represents numerical results performed by traditional integral method with Dieterich law.

3.2 速度步进实验

速度步进实验可用来研究扩容作用及断层泥对动摩擦速度依赖性的影响 （Dieterich and Kilgore，1994）.研究表明，Ruina law能够准确描述摩擦系数对速度变化的响应，即动摩擦的速度依赖性（何昌荣，1999；Dieterich and Kilgore，1994），因而在该算例中选择公式 （3）计算摩擦系数.本实验选择与滑动－保持－滑动实验相同的几何模型（图2），介质参数、数值控制参数及摩擦本构参数见表2.

模拟结果如图5b所示，荷载点速度为10μm／s，滑块稳定滑动；运动25μm后将荷载点速度突然降至1μm／s，运动一段距离后滑块恢复稳定滑动状态，重复上述过程一次.

图5表明，应用速度－状态摩擦本构定律的三维DDA方法能够有效模拟动摩擦的速度依赖性.选择与摩擦实验相同的加载方式和加载条件，三维DDA方法能够比较准确地描述摩擦系数对速度由高值到低值再到高值的响应，曲线形态与实验结果基本吻合.值得注意的是，数值模拟曲线中摩擦系数在速度突变时的响应较实验曲线锐利，通过设置不同的数值弹簧刚度及介质材料参数，并未使得模拟曲线峰尖变缓.分析表明，物理实验的加载（速度变化）做不到数值模拟那样的瞬时响应，因而存在这种差别是合理的.

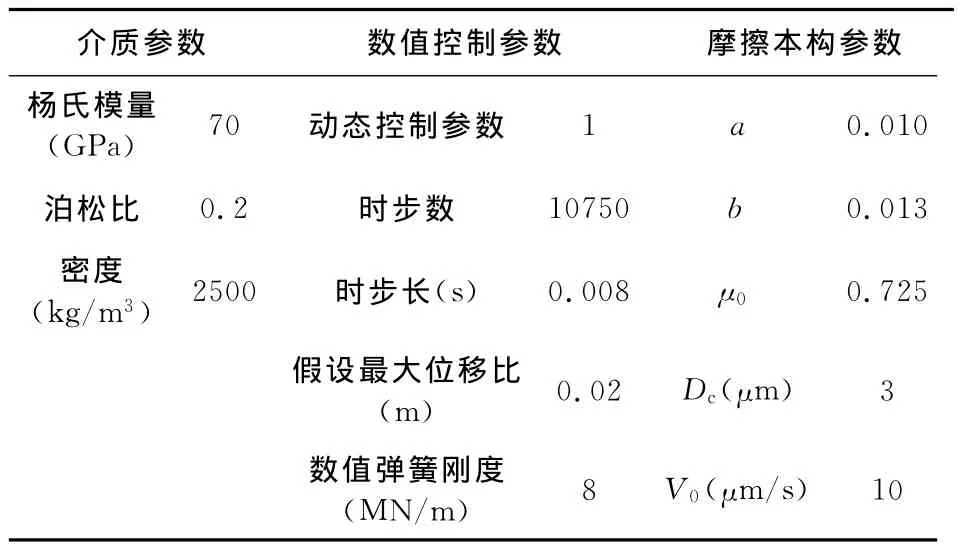
表2 速度步进实验数值参数表Table 2 Numerical parameters of velocity stepping tests for 3DDDA forward modeling simulation

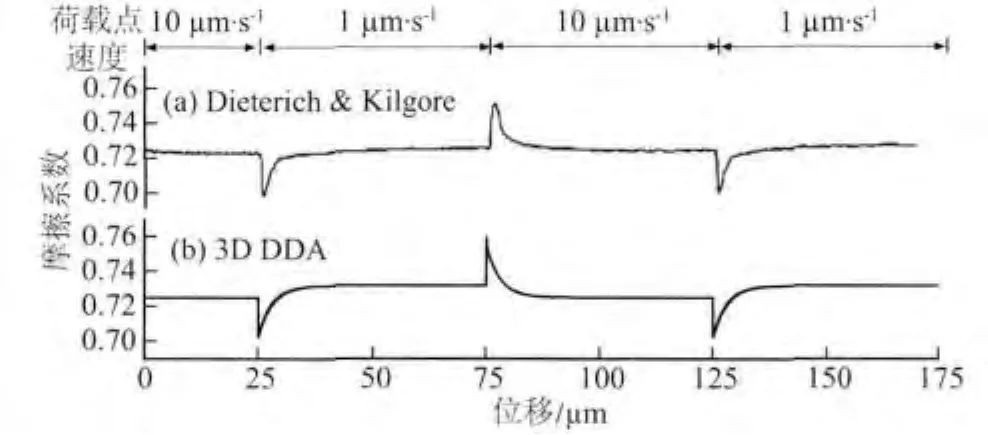
图5 速度步进摩擦实验结果与数值模拟结果Fig.5 Comparison between numerical results and laboratory measurements for velocity stepping tests

4 结论

本文通过公式推导、模型验证等过程，拓展了基于速度－状态摩擦本构定律的三维DDA方法，取得如下认识和结论：

（1）从速度－状态摩擦本构定律的基本形式出发，通过推导给出了融合该定律的三维DDA方法计算摩擦系数的实用公式，拓展了三维DDA方法.

（2）滑动－保持－滑动实验和速度步进实验模拟结果表明，应用速度－状态摩擦本构定律的三维DDA方法可以比较准确地模拟实验中观察到的静摩擦时间依赖性和动摩擦速度依赖性，进而表明该方法模拟接触面剪应力动态变化是有效的.

（3）同原有方法相比，改进后的三维DDA方法解决了应用于大尺度构造应力演化和区域应变积累的基本问题，即Coulomb定律中的常摩擦系数不能反映地震周期中断层面剪应力变化.然而，改进的三维DDA方法在模拟中依然存在由于不连续面刚度的不确定性，发生嵌入深浅不一的问题，往往会影响求解接触力或应力的精度.相信随着三维DDA凹块体接触算法不断完善，本文这种改进将有助于今后与观测资料（GPS等）相结合，定量描述区域地壳变形特征.

致谢感谢石根华先生、九州大学陈光齐教授提供最新版本的三维DDA代码，感谢中国地震局地质研究所何昌荣研究员关于数值模拟技术的有益指导，感谢两位匿名审稿专家为完善本文提出的宝贵意见.

Beeler N M，Tullis T E，Weeks J D.1994.The roles of time and displacement in the evolution effect in rock friction.Geophys.Res.Lett.，21（18）：1987－1990.

Chen B，Jiang Z S，Wang S X，et al.2000.Preliminary study on block movement and its stress field by discontinuous deformation analysis.CrustalDeformationandEarthquake（in Chinese），20（1）：38－42.

Chen Z A，Lin B H，Bai W M.2008.3－D numerical simulation on influence of 1997Mani earthquake occurrence to stability of tectonic blocks system in Qingzang and Chuandian zone using DDA＋FEM method.ChineseJ.Geophys.（in Chinese），51（5）：1422－1430，doi：10.3321／j.issn：0001－5733.2008.05.015.Dieterich J H.1978.Time－dependence friction and the mechanics of stick－slip.PureAppl.Geophys.，116（4－5）：790－806.

Dieterich J H.1979.Modeling of rock friction：1.Experimental results and constitutive equations.J.Geophys.Res.，84（B5）：2161－2168.

Dieterich J H.1981.Constitutive properties of faults with simulated gouge.／／Carter N L，Friedman M，Logan J M eds.Mechanical Behavior of Crustal Rocks：The Handin Volume.Washington，DC：Am.Geophys.Union：24：103－120.

Dieterich J H，Kilgore B D.1994.Direct observation of frictional contacts：new insights for state－dependent properites.Pure Appl.Geophys.，143（1－3）：283－302.

He C R.1999.Comparing two types of rate and state dependent friction laws.SeismologyandGeology（in Chinese），21（2）：137－146.

Lapusta N，Rice J R.2003.Nucleation and early seismic propagation of small and large events in a crustal earthquake model.J.Geophys.Res.，108（B4），doi：10.1029／2001JB00793.Law H K，Lam I P.2003.Evaluation of seismic performance for tunnel retrofit project.J.Geotech.Geoenviron.Eng.，129（7）：575－589.

Liu G，Shu D Q，Jiang Q H.2003.Application of discontinuous deformation analysis method in analyzing shaft well stabilization.Blasting（in Chinese），20（4）：38－44.

Liu L B，Linde A T，Sacks I S，et al.1996.A seismic fault slip and block deformation in north China.PureAppl.Geophys.，146（3－4）：717－740.

Liu Y J，Rice J R.2007.Slow slip predictions based on granite and gabbro friction data compared to GPS measurements in northern Cascadia.J.Geophys.Res.，114（B9）：B09407，doi：10.1029／2008JB006142.

Marone C.1998. Laboratory－derived friction laws and their application to seismic faulting.Annu.Rev.EarthPlanet.Sci.，26：643－696.

Qin X J，Zhou S Y，Zhao L Q，et al.2001.Research on horizontal crustal movement from 1994to 1998in Jiashi and the northeast to Pamir ＆its relation to strong earthquake swarm on the basis of GPS data.CrustalDeformationandEarthquake（in Chinese），21（4）：1－7.

Ruina A L.1983.Slip instability and state variable friction law.J.Geophys.Res.，88（B12）：10359－10370.

Scholz C H.2002.The Mechanics of Earthquakes and Faulting.2nd ed.New York：Cambridge University Press.

Shi G H.1992.Discontinuous deformation analysis：A new numerical model for the statistics and dynamics of deformable block structures.Engng.Comp.，9（2）：157－168.

Shi G H.2001. Three－dimensional discontinuous deformation analysis.／／Elsworth D ed.Proceedings of the 38th U.S.Rock Mechanics Symposium.Taylor ＆Francis，Washington，D.C.，USA，1421－1428.

Sitar N，MacLaughlin M M，Doolin D M.2005.Influence of kinematics on landslide mobility and failure mode.J.Geotech.Geoenviron.Eng.，131（6）：716－728.

Wang H，Zhang G M，Wu Y，et al.2003.The deformation of active crustal－blocks on the Chinese Mainland and its relation with seismic activity.EarthquakeResearchinChina（in Chinese），19（3）：243－254.

Wu A Q，Ding X L，Chen S H，et al.2006.Researches on deformation and failure characteristics of an underground powerhowse with complicated gelolgical conditions by DDA method.ChineseJ.RockMech.Engng.（in Chinese），25（1）：1－8.

Wu J H.2010.Seismic landslide simulations in discontinuous deformation analysis.Comp.Geotech.，37（5）：594－601.

Wu J H，Chen C H.2011.Application of DDA to simulate characteristics of the Tsaoling landslide.Comp.Geotech.，38（5）：741－750.

Wu Y Q，Chen G Q，Jiang Z S，et al.2012.The algorithm of simplex integration in three－dimension and its characteristic analysis.Int.J.Adv.Comp.Tech.，4（10）：246－256.

Zhang L，Jiang Z S，Wu Y Q.2013.Review of rate－and statedependent friction laws and their applications to seismic faulting.ProgressinGeophysics（in Chinese），28（5）：2352－2362，doi：10.6038／pg20130517.

附中文参考文献

陈兵，江在森，王双绪等.2000.利用非连续变形数值方法研究块体运动及其应力场初探.地壳形变与地震，20（1）：38－42.

陈祖安，林邦慧，白武明.2008.1997年玛尼地震对青藏川滇地区构造块体系统稳定性影响的三维DDA＋FEM方法数值模拟.地球物理学报，51（5）：1422－1430，doi：10.3321／j.issn：0001－5733.2008.05.015.

何昌荣.1999.两种摩擦本构关系的对比研究.地震地质，21（2）：137－146.

刘刚，舒大强，姜清辉.2003.应用DDA方法分析竖井爆振稳定问题.爆破，20（4）：38－44.

秦小军，周硕愚，赵齐乐等.2001.依据GPS数据研究伽师及帕米尔东北侧1994—1998年地壳水平运动及其与强震群的关系.地壳形变与地震，21（4）：1－7.

王辉，张国民，吴云等.2003.中国大陆活动地块变形与地震活动的关系.中国地震，19（3）：243－254.

邬爱清，丁秀丽，陈胜宏等.2006.DDA方法在复杂地质条件下地下厂房围岩变形与破坏特征分析中的应用研究.岩石力学与工程学报，25（1）：1－8.

张龙，江在森，武艳强.2013.速度－状态摩擦本构定律及其在地震断层中的应用研究进展.地球物理学进展，28（5）：2352－2362，doi：10.6038／pg20130517.