The Lie-group Shooting Method for Radial Symmetric Solutions of the Yamabe Equation

The Lie-group Shooting Method for Radial Symmetric Solutions of the Yamabe Equation

S.Abbasbandy1,2,R.A.Van Gorder3and M.Hajiketabi1

We transform the Yamabe equation on a ball of arbitrary dimension greater than two into a nonlinear singularly boundary value problem on the unit interval[0,1].Then we apply Lie-group shooting method(LGSM)to search a missing initial condition of slope through a weighting factor r∈(0,1).The best r is determined by matching the right-end boundary condition.When the initial slope is available we can apply the group preserving scheme(GPS)to calculate the solution,which is highly accurate.By LGSM we obtain precise radial symmetric solutions of the Yamabe equation.These results are useful in demonstrating the utility of Lie-group based numerical approaches to solving nonlinear differential equations.

Yamabe equation,nonlinear singularly boundary value problem,group preserving scheme,Lie-group shooting method.

1 Introduction

We then consider the Yamabe boundary value problem

where ∆ is the Laplacian operator and λ is a parameter.In recent years,various methods for solving nonlinear equations and systems have been considered in literature;for example,you can see[T.A.Elgohary,L.Dong,J.L.Junkins,S.N.Atluri(2014a);T.A.Elgohary,L.Dong,J.L.Junkins,S.N.Atluri(2014b);T.Elgohary,D.Kim,J.Turner,J.Junkins(2014)].Equation(1)is strongly nonlinear partial differential equation for any choice of m greater than two.To simplify the situation,we introduce a radially symmetric function and radial variable by

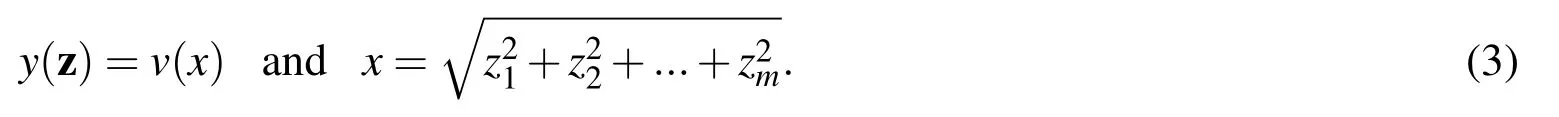
Let us also pick the constant

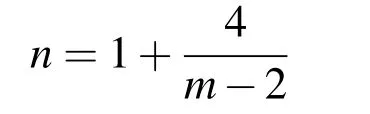
so that for m≥3 we have n∈(1,5].Then the boundary value problem(1)-(2)is put into the form

We should remark that(4)is similar in form to the Lane-Emden equation of the first kind which has been considered in the literature.Note that(4)has an extra term,and that the form of the conditions is different(the relevant Lane-Emden problem is an initial value problem,not a boundary value problem).Both λ and n are parameters.We can take λ to be a real number,whereas n depends on m:If m=3,n=5;if m=4,n=3;if m=5,n=7/3;and so on.As m tends to infinity,n tends to one,so the problem is linear in this limit and the problem can be solved exactly.In this paper we solve eqs.(4)and(5)that has been less attention for various λ and m via the Lie group shooting method and obtain radial symmetric solutions of the Yamabe equation.we show agreement between numerical solution and the exact solution in the large m case.

The Lie group shooting method is based on the group-preserving scheme(GPS),created previously by[C.-S.Liu(2001)]for solving the IVP of ODEs.Liu[C.-S.Liu(2006a);C.-S.Liu(2006b);C.-S.Liu(2006c);C.-S.Liu(2012a)]has developed the GPS to solve the BVPs.In the formation of the Lie-group method for the solutions of BVPs,Liu[C.-S.Liu(2006b)]has presented the concept of one-step GPS by utilizing the closure property of the Lie-group,and hence,the new shooting method had been named the Lie-group shooting method(LGSM).Because the Lie-group method has certain advantages than other numerical methods due to its Lie-group structure,is shown to be a powerful technique to solve the various problems[S.Abbasbandy,M.S.Hashemi,C.-S.Liu(2011);C.W.Chang,J.R.Chang,C.-S.Liu(2006);C.W.Chang,J.R.Chang,C.-S.Liu(2008);C.-S.Liu(2006a);C.-S.Liu(2006b);C.-S.Liu(2006c);C.-S.Liu(2006d);C.-S.Liu(2008);C.-S.Liu(2009);C.-S.Liu(2010);C.-S.Liu(2011);C.-S.Liu(2012a);C.-S.Liu(2012b);C.-S.Liu(2012c);C.-S.Liu,(2012d);C.-S.Liu(2013a);C.-S.Liu(2013b);C.-S.Liu,(2013c);C.-S.Liu,C.W.Chang,J.R.Chang(2008);C.-S.Liu,J.R.Chang(2008);C.-S.Liu,(2014)].

This paper is organized as follows.In section 2 we give a short sketch of the GPS for ODEs,explain the making of one-step GPS by using the closure property of the Lie-group,and find out it through a single-parameter Lie-group element in terms of a parameter r and through a universal one-step Lie-group element.In section 3 we derive a Lie-group shooting method to solve BVPs,where a missing initial condition is derived in a closed-form in terms of r in a range of r∈(0,1)and we obtain r by matching the right boundary condition.In section 4 we convert the Yamabe equation to an equation with equal value boundary conditions that is very important in LGSM and present the numerical results of the LGSM on the Yamabe problem for different values of λ and m that represents solutions with good accuracy.

2 One-step group-preserving scheme

2.1 The GPS

Many physical systems can be writte as

where

It is very important in the Lie group shooting method that we replace the originally un-equal boundary conditions by the boundary conditions with an equal value.Liu[C.-S.Liu(2001)]has embedded Eq.(6)into an augmented differential system:

whereAis an element of the Lie-algebra so(2,1)satisfying

with

a Minkowski metric.Here,I2is the identity matrix,and the superscript T stands for the transpose.The augmented variableXautomatically satisfies the cone condition:

Accordingly,Liu[C.-S.Liu(2001)]has developed a group-preserving scheme(GPS)given as follows:

whereXkdenotes the numerical value ofXat the discrete xk,andG(k)∈SOo(2,1)satisfies

2.2 Generalized mid-point rule

Applying scheme(13)to Eq.(9)with a specified initial conditionX0,we can compute the solutionX(x)by GPS.Assuming that the stepsize used in GPS is∆x=(β −α)/k and starting from an initial augmented conditionwe want to calculate the valueat x= β.By applying Eq.(13)step-by-step we can obtain

whereXfapproximates the exactXfwith a certain accuracy depending on∆x.However,let us recall that eachGi,i=1,2,...,k is an element of the Lie group SOo(2,1)and by the closure property of Lie groupGk(∆x)...G1(∆x),is also a Lie group denoted byG.Hence,we have

This is a one-step transformation fromX0toXf.

Theoretically,such a one-stepGexists,and the remaining problem is how to determineG.While an exact solution ofGis not available,we can calculateGthrough a numerical method by a generalized mid-point rule,which is obtained from an exponential mapping ofAby taking the values of the argument variables ofAat a generalized mid-point.The Lie group generated formA∈so(2,1)is known as a proper orthochronous Lorentz group,which admits a closed-form representation:

where

Here,we use the initialand the finalthrough a suitable weighting factor r to calculateG,where 0＜r＜1 is a parameter and.The above method employed a generalized mid-point rule to calculateG,and the resultant is a single-parameter Lie group elementG(r).In section 3 we will describe a process to find a suitable r∈(0,1).

The approach of Eq.(19)can be realized alternatively by using

Integrating the above equation and using the mean-value theorem we obtain

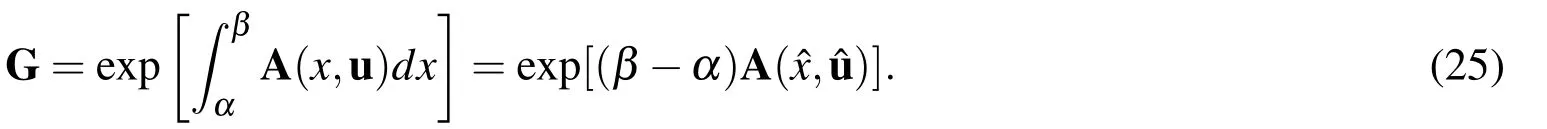
Inserting Eq.(9)for A and calculating the exponential we can derive Eqs.(19)-(23)again.

2.3 A universal Lie-group mapping between two points on the cone

Now we define a new vector

such that Eqs.(19),(22)and(23)can also be expressed as

From Eqs.(18)and(27)the one-step Lie-group transformation is written as

where

Substituting

into Eq.(31)and dividing both the sides by ‖u0‖,we can obtain

where

are obtained by inserting Eq.(33)forFinto Eqs.(28)and(29).Let

and

where 0≤θ≤π is the intersection angle between vectorsuf−u0andu0,and thus from Eqs.(34)-(36)it follows that

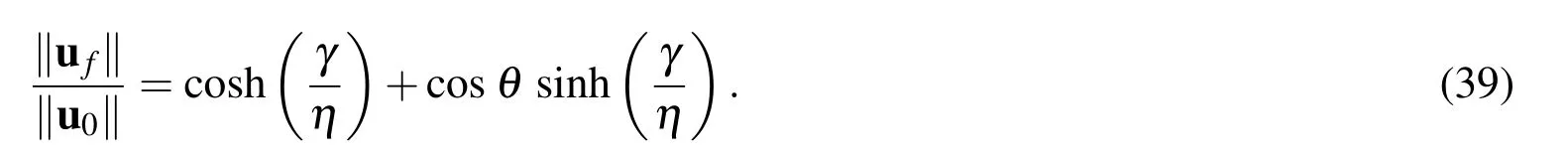
Upon defining

from Eq.(39)we obtain a quadratic equation for Z:

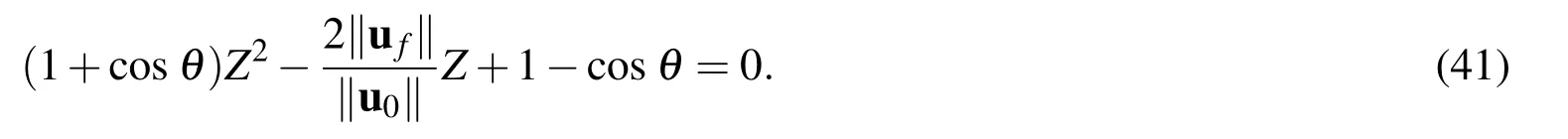
The solution is found to be

and thus from Eqs.(40)and(38)we can compute η by

Therefore,between any two pointsandon the cone,there exists a Lie-group elementG∈ SO0(2n,1)mappingonto

whereGis uniquely determined byu0andufthrough Eqs.(27),(28),(29),(33),(37),(42)and(43).We write thisGto beG(u0,uf),in order to emphasize it as being a Lie-group mapping between the quantities ofu0anduf,which are the values ofuoccurred at two ends of a whole interval of x∈ [α,β].

The aboveis different from the one in Eq.(19).These two Lie-group elementsG(r)andare constructed by different manners.When the former is an approximation by using the generalized mid-point rule,the latter is a universal mapping betweenandindependent to the vector fieldfand the parameter r,which means that such a mapping is applicable to all ODEs systems.

3 The Lie-group shooting method

It is interesting that by puttingwe can conclude the required equations for finding the missing initial condition.From Eqs.(6)-(8)it follows that

where A and B are two unknown constants,and c is a given positive constant determined by the user.From Eqs.(33),(47)and(48)it follows that

From Eqs.(43),(42)and(37)by inserting Eq.(8)foruand noting that

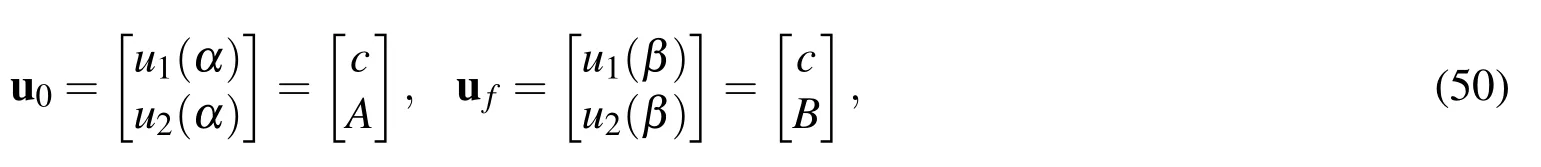
we obtain

where

By comparing Eq.(49)with Eq.(26),with the aid of Eqs.(20),(21),(47)and(48)we obtain

where

The above derivation of the governing equations(54)-(57)is based on by equating the two F in Eqs.(49)and(26).It also means that the two Lie group elements defined by Eqs.(19)and(27)are equal.In this sense we may call our shooting technique a Lie-group shooting method.

3.1 The solution of A

Firstly,Liu[C.-S.Liu(2006b)]analytically solved A for general second-order BVPs.Remarkably,Eqs.(54)and(55)can be used to solve A exactly.From Eqs.(54)and(57)it follows that

which is a positive constant.This equation is very important to reduce our following works to conclude a closed-form solution of A in terms of r.This is the reason that we replace the originally un-equal boundary conditions by the boundary conditions with an equal value in Eq.(7),which lends to rA+(1−r)B=0 as shown in Eq.(54),and hence ξ defined by Eq.(57)becomes a constant as shown in Eq.(58).Hence,from Eq.(55)with the aid of Eqs.(51)-(54),(56)and(58)we can obtain a single algebraic equation for solving the unknown variable A:

where

and B=rA/(r−1)has a different sign with A due to r∈(0,1).Eq.(59)can be used to solve A for a given r.If A is available,we can return to Eqs.(45)-(48)and integrate them by a suitable IVP solver.

3.2 The case of A＞0

Here we first consider the case of A ＞ 0.Inserting Eq.(62)for η0into Eq.(59)we obtain

Defining

and substituting Eq.(61)for Z into Eq.(63)we obtain

By using A＞0 and B＜0,Eq.(65)can be written as

Squaring the above equation and cancelling out the common terms we can rearrange it to

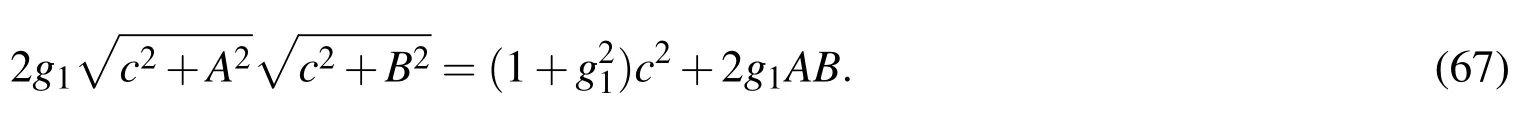
Squaring again and cancelling out the common term and factor we can obtain

Inserting B=rA/(r−1)and through some algebraic manipulations we eventually obtain

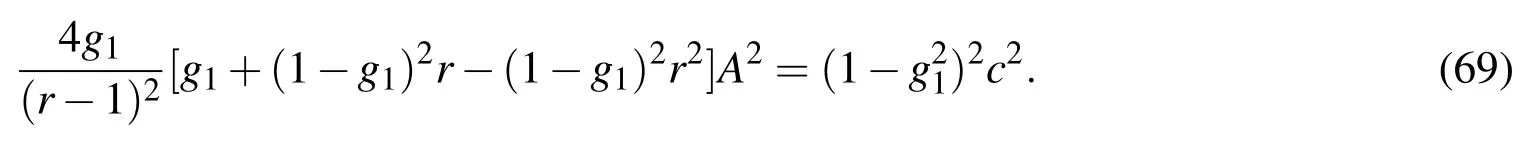
If the following condition holds

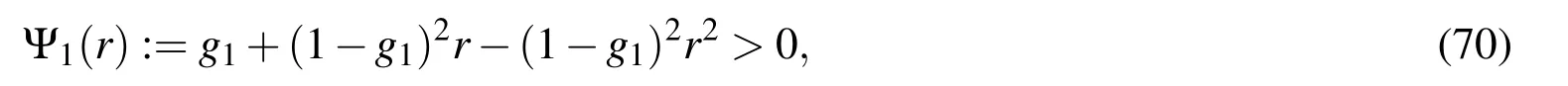
then A has a positive solution:

The condition(70)can be used to identify the range where r is permitted.

3.3 The case of A＜0

Next we consider the case of A ＜ 0.Inserting Eq.(62)for η0into Eq.(59)we obtain

Defining

and substituting Eq.(61)for Z into Eq.(72)we obtain

By using A＜0 and B＞0,Eq.(74)can be written as

Squaring the above equation and cancelling out the common terms we can rearrange it to

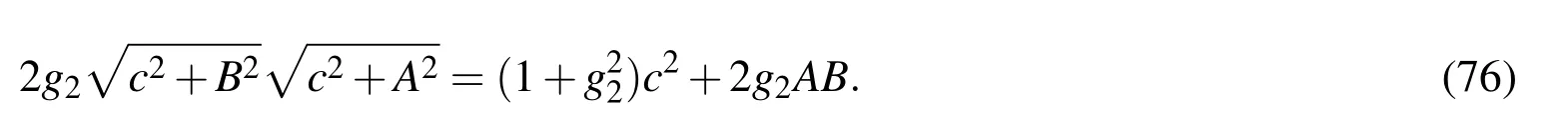
Squaring again and cancelling out the common term and factor we can obtain

Inserting B=rA/(r−1)and through some algebraic manipulations we eventually obtain

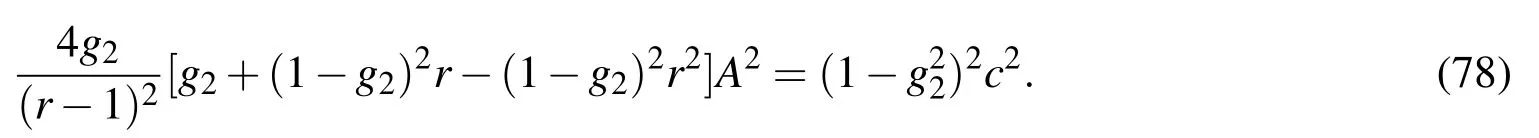
If the following condition holds

then A has a negative solution:

3.4 Adjusting the slope A

In the previous two subsections we have derived two closed-form formulae to calculate the slope A for each r in its admissible range.If A is available,we can apply the GPS to integrate the(u,x)-IVP in Eqs.(45)-(48).Up to this point we should note that the Lie-group shooting method is an exactly solving technique for the second-order nonlinear BVPs without making any assumption or the approximation in derivations of all required formulas.

Now,in order to determine a correct r and thus a correct A,we need a numerical integration of the nonlinear ODEs in Eqs.(45)-(48)via a shooting technique.For a trial r in the admissible range,we can calculate A and then numerically integrate Eqs.(45)-(48)from x=α to x=β,and compare the end value ofwith the exact one u1(β)=c.Ifis smaller than a given error tolerance ε,then the process of finding the solution of A is finished.Otherwise,we need to calculate the end values of u1(β)corresponding to different r1＜ r and r2＞r,which are denoted byand,respectively.Ifthen there exists one root between r1and r;otherwise,the root is located between(r,r2).Continuing this process we can quickly select a suitable r to satisfy the criterion of

3.5 The GPS

We have derived the closed-form solutions to calculate the slope A for each r in its admissible range,and thus we can integrate the(u,x)-IVP in Eqs.(45)-(48)by the GPS method.The Lie group generated fromA∈so(2,1)is known as a proper orthochronous Lorentz group.An exponential mapping ofA(n)admits the closed-form representation:

where

Substituting the above exp[∆xA(n)]forGinto Eq.(18)and taking its first row,we obtain

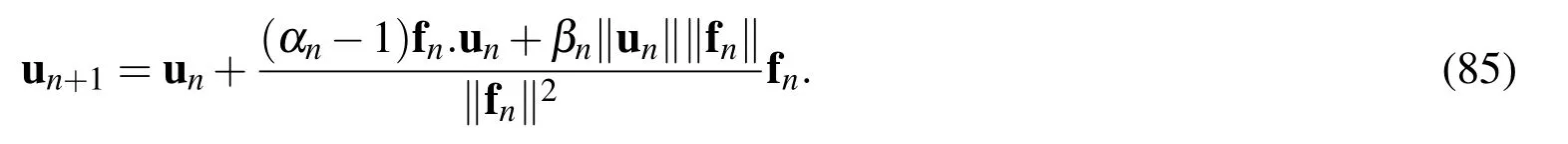
The numerical scheme(85)was first derived by Liu[C.-S.Liu(2001)].We use from(85)to integrate IVPs.The major difference between GPS and the traditional numerical methods is that those schemes are all formulated directly in the usual Euclidean space Rn;none of them are considered in the Minkowski space Mn+1.One of the benefits of GPS in the augmented Minkowski space is that the resulting schemes can avoid the spurious solutions and ghost fixed points.

4 The Yamabe equation

We consider eqs.(4)and(5)and use the following transformation:

Therefore,the Yamabe problem is transformed to the following problem:

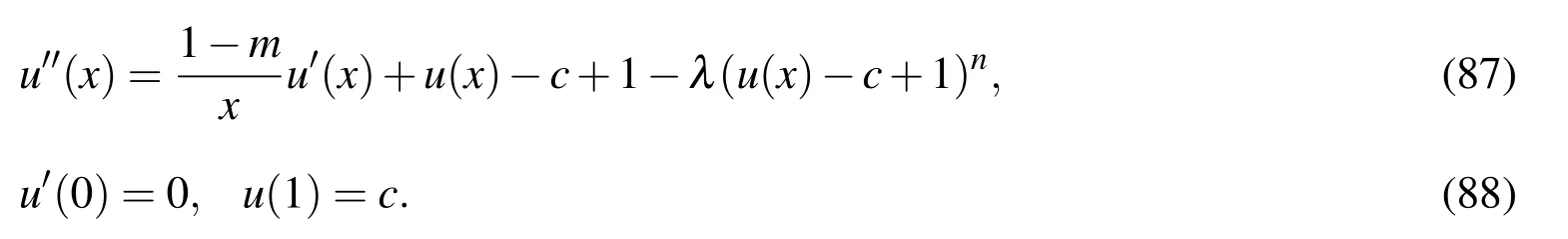
Then,we convert Eqs.(87)and(88)to the following system:

where

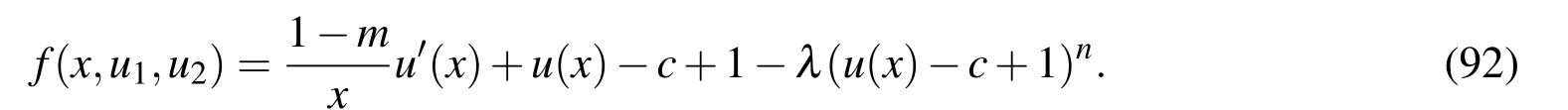
Now,consider the following equation:

where

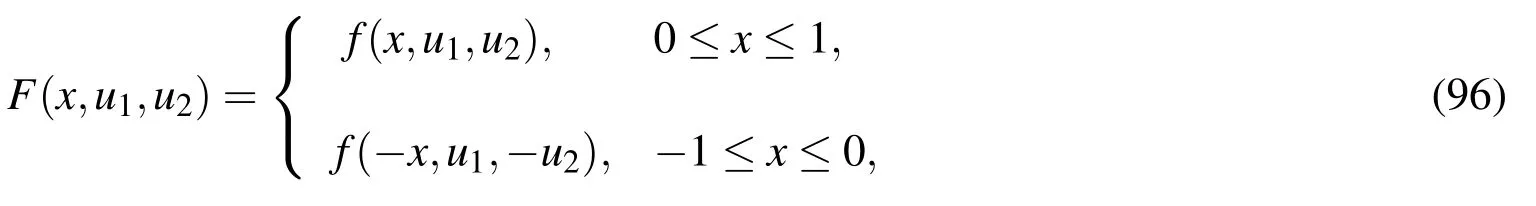
is a symmetric extension of Eq.(90).As explained in previous section we can apply LGSM for Eqs.(93)-(96)on[−1,1],but in practical numerical calculations we only need to calculate the above equations from x=−1 to x=0,where we adjust the slope u2(−1)=A by the method in 3.4.If the target equation u′(0)=0 is satisfied then we obtain the numerical solution by merely mapping the solution into the interval of 0≤x≤1.

4.1 Numerical results

The Yamabe equation has the exact solution v(x)=1 for λ=1.we consider u2(−1)=A ＜ 0 for cases λ ＜ 1 and u2(−1)=A ＞ 0 for cases λ ＞ 1 and apply the Lie group shooting method.In order to avoid over flow in computations we can select a suitable c for different λ.In the Tables Tab.1 and Tab.2 are shown the parameters used in the Lie group shooting method for λ =0.1,λ = −1,λ =2,λ =4 and various m.In the Figure Fig.1 we show two examples for error mis-maching plot respect to r.We show the solutions obtained for the Yamabe equation using the Lie group shooting method for λ =0.1,λ = −1,λ =2,λ =4 and various m in the Figures Fig.2 and Fig.3.Figure Fig.4 show the residual error of solution Eqs.(4)and(5)for λ =0.1 and λ =2 and different m.We should point out that we use ofin Eq.(4)for obtain the residual error that v′(xi)calculated by LGSM.In Figure Fig.5 we show symmetric radial solutions of the Yamabe respect to v(x)=1 and that whenever the parameter m becomes large the solution converges to v(x)=1.Finally,in the Tables Tab.3-Tab.8 we compared results obtained for v(x)and v′(x)through LGSM for λ = −1 and λ =4 with the MIDRICH(midpoint method with Richardson extrapolation[L.Lapidus and J.H.Seinfeld(1971)])that is a powerful method for solving the singular problems.This comparison shows the accuracy of LGSM.

5 Conclusions

In this paper we obtain solutions for the Yamabe equation for different values of λ via the Lie group shooting method.Lie-group shooting method was developed to derive algebraic equations to find the missing initial condition.Furthermore,by adjusting the boundary conditions from the one of un-equal boundary-value to the one with equal boundary-value,the present approach can provide a closed-form formula to calculate the missing initial condition without need of any iteration.

Figure 1:Plot of u′(0)− 0 respect to r for λ =0.1 and m=3(left),λ =2 and m=4(right).

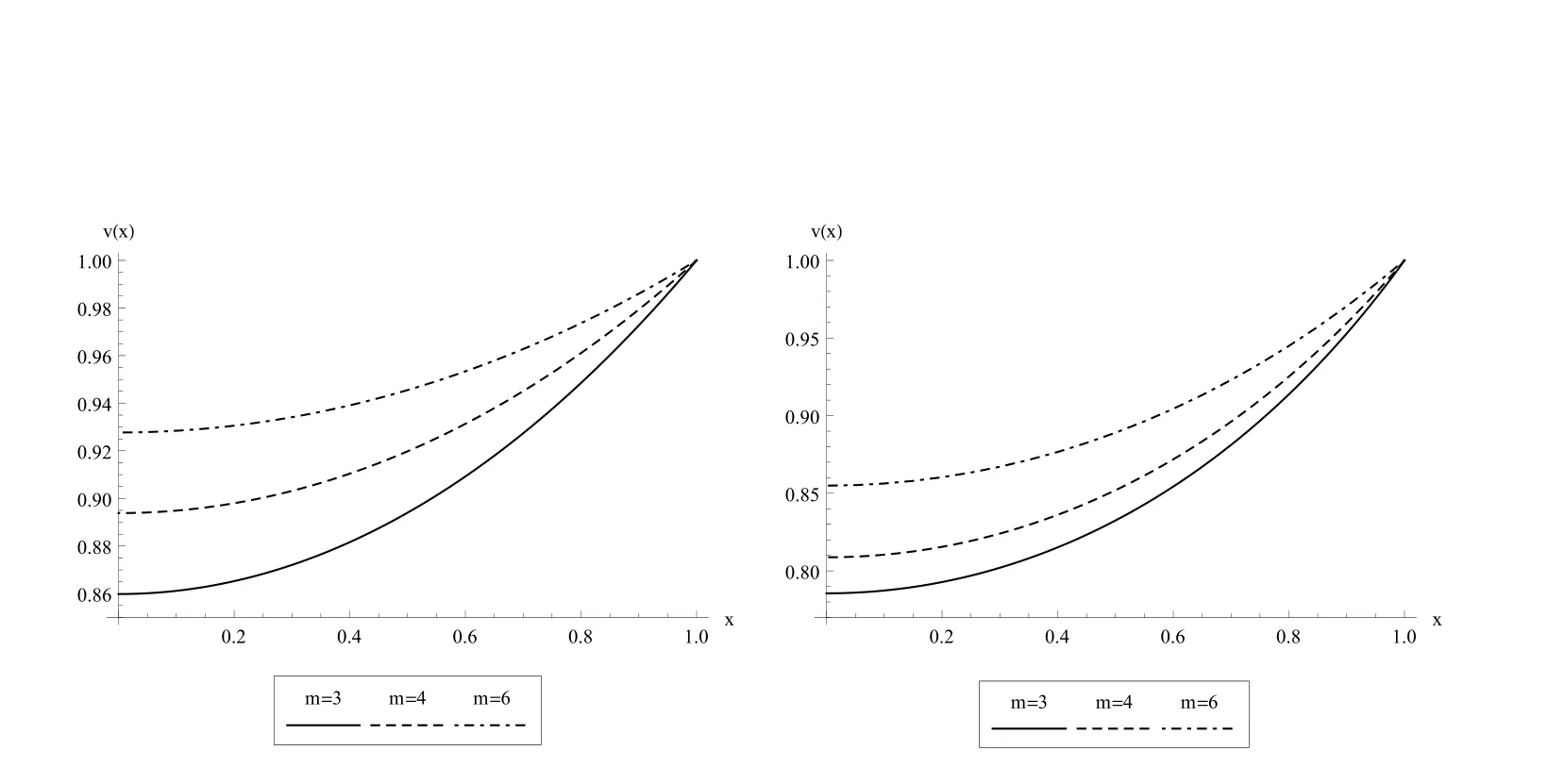
Figure 2:Numerical solutions obtained using LGSM for λ =0.1(left)and λ = −1(right).

Table 1:Parameters used for λ =0.1(up)and λ = −1(down).

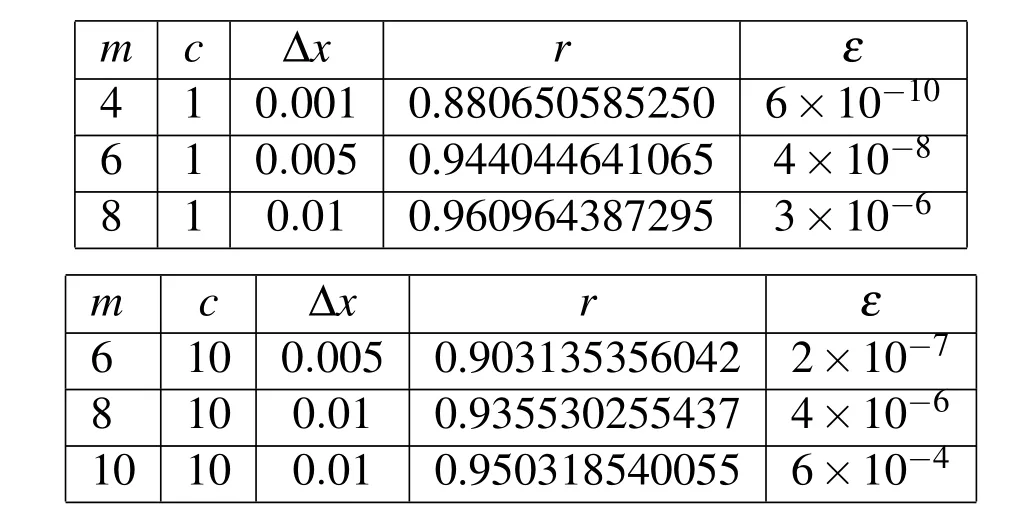
Table 2:Parameters used for λ =2(up)and λ =4(down).

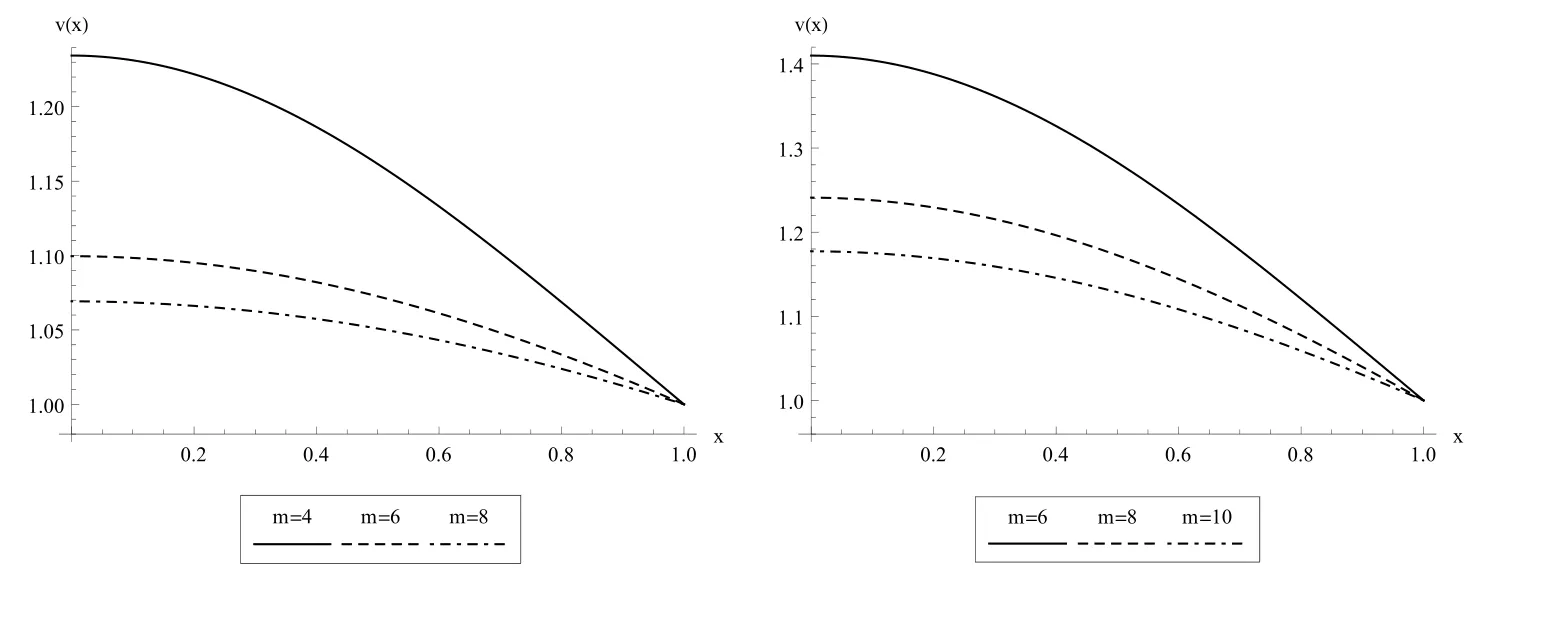
Figure 3:Numerical solutions obtained using LGSM for λ =2(left)and λ =4(right).

Figure 4:Residual error obtained using LGSM for λ =0.1(left)and λ =2(right).

Figure 5:Plot of the radial symmetric solutions to the Yamabe equation for λ = −1 and λ =4 and also

Table 3:Comparison of numerical results obtained by LGSM and MIDRICH for λ=−1,m=3.

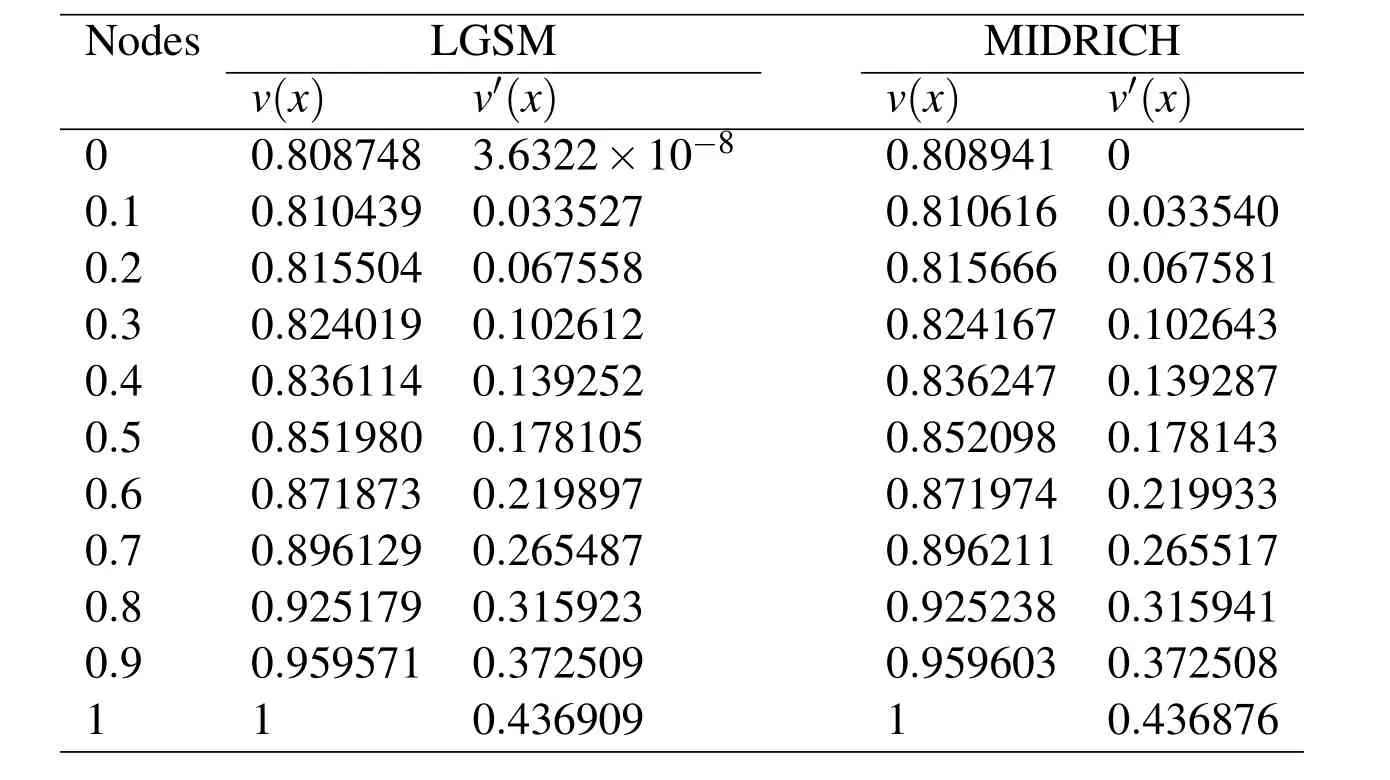
Table 4:Comparison of numerical results obtained by LGSM and MIDRICH for λ=−1,m=4.

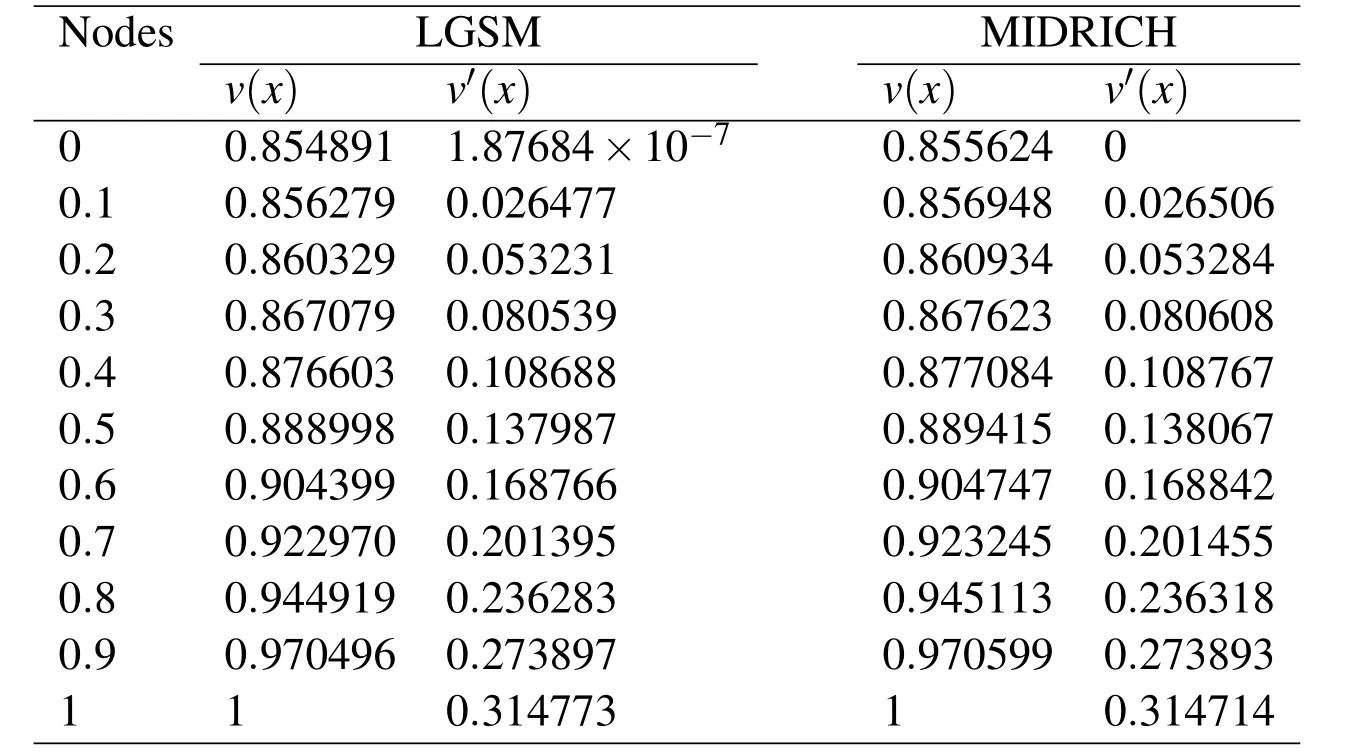
Table 5:Comparison of numerical results obtained by LGSM and MIDRICH for λ=−1,m=6.

Table 6:Comparison of numerical results obtained by LGSM and MIDRICH for λ=4,m=6.

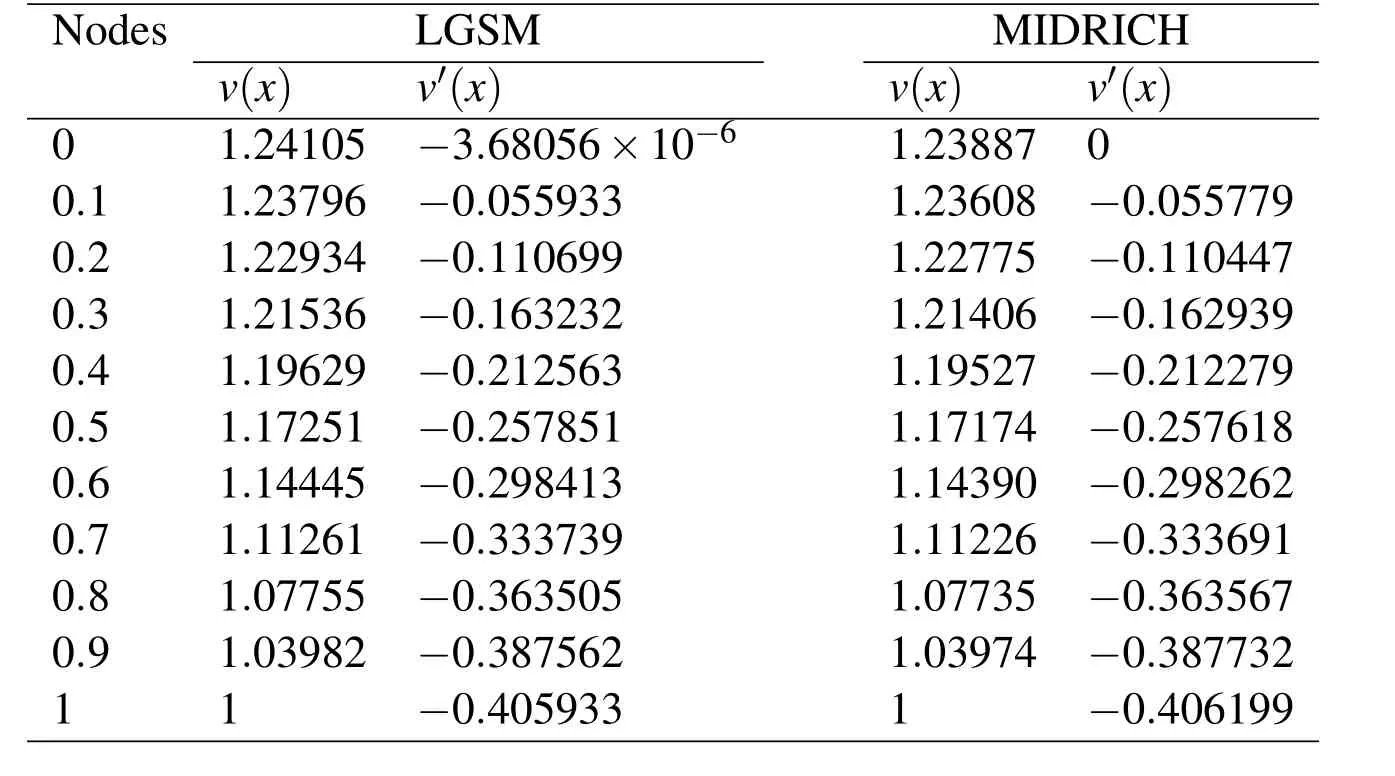
Table 7:Comparison of numerical results obtained by LGSM and MIDRICH for λ=4,m=8.

Table 8:Comparison of numerical results obtained by LGSM and MIDRICH for λ=4,m=10.

Therefore,we can determine r very quickly through only a few trials.From the numerical results,it is clear that for values λ＜1 solutions are ascending and for values λ＞1 are descending but whenever the parameter m becomes large the solution converges to v(x)=1(exact solution for λ=1).Compared with other numerical methods,the new approach is shown to be accurate.

Acknowledgement:We thank the anonymous reviewers for helpful comments,which lead to definite improvement in the manuscript.

Abbasbandy,S.;Hashemi,M.S.;Liu,C.-S.(2011): The Lie-group shooting method for solving the Bratu equation.Commun.Nonlinear Sci.Numer.Simulat.,vol.16,pp.4238–49.

Alice Chang,S.Y.;Han,Z.C.;Yang,P.(2005):Classification of singular radial solutions to the σkYamabe equation on annular domains.J.Differential Equations,vol.216,pp.482–501.

Andersson,L.;Chrusciel,P.T.;Friedrich,H.(1992): On the regularity of solutions to the Yamabe equation and the existence of smooth hyperboloidal initial data for Einstein’s field equations.Comm.Math.Phys.,vol.149,pp.587–612.

Bhrawy,A.H.;Alofi,A.S.;Van Gorder,R.A.(2014):An efficient collocation method for a class of boundary value problems arising in mathematical physics and geometry.Abs.Appl.Anal.,Vol.2014,ID:425648.

Brendle,S.(2008):Blow-up phenomena for the Yamabe equation.J.Amer.Math.Soc.,vol.21,pp.951–980.

Chang,C.W.;Chang,J.R.;Liu,C.-S.(2006):The Lie-group shooting method for boundary layer equations in fluid mechanics.J.Hydrodyn.,vol.18,pp.103–108.

Chang,C.W.;Chang,J.R.;Liu,C.-S.(2008):The Lie-group shooting method for solving classical Blasius flat-plate problem.Computers,Materials and Continua,vol.7,pp.139–153.

Elgohary,T.A.;Dong,L.;Junkins,J.L.;Atluri,S.N.(2014a):A simple,fast,and accurate time-integrator for strongly non-linear dynamical systems.Comput.Model Eng.Sci.,vol.100,pp.249–275.

Elgohary,T.A.;Dong,L.;Junkins,J.L.;Atluri,S.N.(2014b): Time domain inverse problems in nonlinear systems using collocation radial basis functions.Comput.Model Eng.Sci.,vol.100,pp.59–84.

Elgohary,T.A.;Dong,L.;Junkins,J.L.;Atluri,S.N.(2014):An efficient algorithm for perturbed orbit integration combining analytical continuation and modified chebyshev picard iteration.Advanced Maui Optical and Space Surveillance Technologies Conference,vol.1,pp.18.

Lapidus,L.;Seinfeld,J.H.(1971): Numerical solution of ordinary differential equations,Mathematics in Science and Engineering.Vol.74,Academic Press,New York-London.

Liu,C.-S.(2001): Cone of non-linear dynamical system and group preserving schemes.Int.J.Non-Linear Mech.,vol.36,pp.1047–1068.

Liu,C.-S.(2006a): Efficient shooting methods for the second order ordinary differential equations.Comput.Model Eng.Sci.,vol.15,pp.69–86.

Liu,C.-S.(2006b): The Lie-group shooting method for nonlinear two-point boundary value problems exhibiting multiple solutions.Comput.Model Eng.Sci.,vol.13,pp.149–63.

Liu,C.-S.(2006c):The Lie-group shooting method for singularly perturbed twopoint boundary value problems.Comput.Model Eng.Sci.,vol.15,pp.179–96.

Liu,C.-S.(2006d): A group preserving scheme for Burgers equation with very large Reynolds number.Comput.Model Eng.Sci.,vol.12,pp.197–211.

Liu,C.-S.(2008):A Lie-group shooting method for computing eigenvalues and eigenfunctions of Sturm-Liouville problems.Comput.Model Eng.Sci.,vol.26,pp.157–68.

Liu,C.-S.(2009): A two-stage LGSM to identify time-dependent heat source through an internal measurement of temperature.Int.J.Heat Mass Transfer,vol.52,pp.1635–1642.

Liu,C.-S.(2010):The Lie-group shooting method for computing the generalized Sturm-Liouville problems.Comput.Model Eng.Sci.,vol.56,pp.85–112.

Liu,C.-S.(2011):The Lie-group shooting method for boundary-layer problems with suction/injection/reverse flow conditions for power-law fluids.Int.J.Non-Linear Mech.,vol.46,pp.1001–1008.

Liu,C.-S.(2012a):The Lie-group shooting method for solving multi-dimensional nonlinear boundary value problems.J.Optim.Theory Appl.,vol.152,pp.468–495.

Liu,C.-S.(2012b):Computing the eigenvalues of the generalized Sturm-Liouville problems based on the Lie-group SL(2,R).J.Comput.Appl.Math.,vol.236,pp.4547–4560.

Liu,C.-S.(2012c):A Lie-group shooting method for reconstructing a past timedependent heat source.Int.J.Heat Mass Transfer,vol.55,pp.1773–1781.

Liu,C.-S.(2012d):The optimal control problem of nonlinear Duffing oscillator solved by the Lie-group adaptive method.Comput.Model Eng.Sci.,vol.86,pp.171–197.

Liu,C.-S.(2013a):Developing an SL(2,R)Lie-group shooting method for a singular φ-Laplacian in a nonlinear ODE.Commun.Nonlinear Sci.Numer.Simulat.,vol.18,pp.2327–2339.

Liu,C.-S.(2013b): An SL(3,R)shooting method for solving the Falkner-Skan boundary layer equation.Int.J.Non-Linear Mech.,vol.49,pp.145–151.

Liu,C.-S.(2013c):A GL(n,R)differential algebraic equation method for numerical differentiation of noisy signal.Comput.Model Eng.Sci.,vol.92,pp.213–239.Liu,C.-S.;Chang,C.W.;Chang,J.R.(2008): A new shooting method for solving boundary layer equation in fluid mechanics.Comput.Model Eng.Sci.,vol.32,pp.1–15.

Liu,C.-S.;Chang,J.R.(2008): The Lie-group shooting method for multiplesolutions of Falkner-Skan equation under suction-injection conditions.Int.J.Non-Linear Mech.,vol.43,pp.844–851.

Liu,C.-S.(2014):An LGDAE method to solve nonlinear Cauchy problem without initial temperature.Comput.Model Eng.Sci.,vol.99,pp.371–391.

Van Gorder,R.A.(2012): Control of error in the homotopy analysis of semilinear elliptic boundary value problems.Numer.Algorithms,vol.61,pp.613–629.

1Department of Mathematics,Imam Khomeini International University,Ghazvin 34149,Iran.

2Corresponding author.Tel:+98-912-1305326;Fax:+98-283-3901312;E-mail:abbasbandy@yahoo.com(S.Abbasbandy)

3Mathematical Institute,University of Oxford,Andrew Wiles Building,Radcliffe Observatory Quarter,Woodstock Road,Oxford,OX2 6GG,United Kingdom