A Continuum Shell Model Including van der Waals Interaction for Free Vibrations of Double-Walled Carbon Nanotubes

2015-12-12 06:47

Computer Modeling In Engineering&Sciences 2015年4期

Salvatore Brischetto1

This paper proposes the free vibration analysis of Double-Walled Carbon NanoTubes(DWCNTs).A continuum elastic three-dimensional shell model is used for natural frequency investigation of simply supported DWCNTs.The 3D shell method is compared with beam analyses to show the applicability limits of 1D beam models.The effect of van der Waals interaction between the two cylinders is shown for different Carbon NanoTube(CNT)lengths and vibration modes.Results give the van der Waals interaction effect in terms of frequency values.In order to apply the 3D shell continuum model,DWCNTs are de fined as two concentric isotropic cylinders(with an equivalent thickness and Young modulus)which can be linked by means of the interlaminar continuity conditions or by means of an in finitesimal fictitious layer which represents the van der Waals interaction.

Exact solution,three-dimensional shell model,double-walled carbon nanotube,van der Waals interaction,free vibration.

1 Introduction

Carbon NanoTubes(CNTs)are closed graphene sheets with a cylindrical shape,they were discovered in Japan by Iijma in 1991[Iijma(1991)].CNTs exhibit exceptional mechanical properties[Valava and Odegard(2005);Srivastava and Atluri(2002)],the equivalent elastic modulus is usually greater than 1 TPa and the tensile strength exceeds that of steel by over one order of magnitude.For these reasons,CNTs are considered to be ideal reinforcements in composite structures[Rouainia and Djeghaba(2008);Wu and Jiang(2014);Ghouhestani et al.(2014)].

The behavior of CNTs can be simulated by means of three different basic methods[Qian et al.(2002)]:Molecular Dynamic(MD)simulations,atomistic-basedmodelling approaches and continuum approaches.In the MD approaches,the simulations are based on the definition of an appropriate potential energy function(e.g.,Tersoff-Brenner or Lennard-Jones functions)[Chen and Cao(2006);Hu et al.(2012);Ansari et al.(2012);Chowdhury et al.(2010);Das et al.(2013);Zhang et al.(2009);Sinnott et al.(2002);Brenner et al.(2002);Yang et al.(2002);Namilae et al.(2007)].In the atomistic-based modelling approaches,CNTs are investigated by means of an atomistic finite element model with beam elements and concentrated masses.The beams simulate the interatomic covalent forces and the masses(which are located at the ends of the beams)represent the carbon positions[Arghavan and Singh(2011);Gupta et al.(2012);Mir et al.(2008);Yan et al.(2008);Aydogdu(2009);Yan et al.(2013)].The continuum approaches are based on the assumption that carbon nanotubes(which have a discrete molecular structure)are continuum isotropic elastic cylinders which can be analyzed via beam or shell models.When a continuum elastic model is applied to CNT analysis,it is of central importance to accurately quantify the elastic properties of Single-Walled CNTs(SWCNTs)and Double-Walled CNTs(DWCNTs)[Wang and Zhang(2008a)].

The high computational cost of the MD simulations of complex CNT networks does not allow fast analyses.A real size multi-walled CNT simulation by means of an atomistic-based modelling approach is also expensive.Therefore,continuum approaches are preferred to MD and atomistic-based models in the described simulations because of their better computational cost.In order to apply a continuum model,it is necessary to correctly de fine effective CNT wall thickness,Young modulus and Poisson ratio because a carbon nanotube has a discrete molecular structure.Extensive studies[Vodenitcharova and Zhang(2003);Odegard et al.(2002);Lee and Oh(2008);Zhang(2009)]have been conducted to analyze this feature.A final conclusion has not yet been reached,as demonstrated by the different thickness and Young modulus values shown in the papers analyzed below.These equivalent properties are not always the same for a given elastic stiffness.

Many researchers have used beam models for continuum approaches to analyze free vibrations of single-walled and multi-walled carbon nanotubes.Among Single-Walled Carbon Nanotube(SWCNT)simulations,Araújo dos Santos(2011)used finite elements based on the Euler-Bernoulli and Timoshenko beam theories.The Timoshenko beam model with generalized boundary conditions was also employed by Azrar et al.(2011).Unlike the Euler-Bernoulli beam model,the Timoshenko beam model allows for the effects of transverse shear deformation and rotary inertia[Benzair et al.2008].Demir et al.(2010)used the discrete singular convolution(DSC)method based on the Timoshenko beam theory.Foda(2013)proposed a direct analytical approach to suppress the steady state vibrations of a SWCNT rest-ing on a Winkler foundation.The natural frequencies and transversal responses of simply supported SWCNTs were analyzed in Horng(2012)by means of the Timoshenko beam theory and the Bernoulli-Fourier method.The thermal vibrations of SWCNTs were analyzed by Ming and Huiming(2013)by means of a single beam model.The nonlocal elasticity was incorporated to introduce the effects of small size into the formulation.The Timoskenko beam finite element formulation was used in Swain et al.(2013)for the flexural vibration of SWCNTs.The nonlinear vibration of a SWCNT(considered as a curved beam subjected to a harmonic load)was investigated in Wang et al.(2013)by means of the nonlocal continuum theory.A stress gradient and a strain gradient approach were used in Wang and Wang(2013)where vibrations of nanotubes embedded in an elastic matrix were investigated by means of the nonlocal Timoshenko beam model.The nonlocal Euler-Bernoulli and Timoshenko beam theories were used in Soltani et al.(2012)to investigate the transverse vibration of a single-walled carbon nanotube with light waviness along its axis.The comparison between the two beam models shows the effects of transverse shear deformation and rotary inertia.Forced vibrations of a simply supported SWCNT subjected to a moving harmonic load were analyzed in Simsek(2010)by means of the nonlocal Euler-Bernoulli beam theory.Murmu and Pradhan(2009)developed a nonlocal elasticity Timoshenko beam model to investigate the stability response of a SWCNT embedded in an elastic medium.Both Winkler-type and Pasternak-type foundation models were employed to simulate the interaction of the SWCNT with the surrounding elastic medium.Different beam theories including those of Euler-Bernoulli,Timoshenko,Reddy,Levinson and Aydogdu were compared in Aydogdu(2009a).Non local constitutive equations of Eringen were used for these comparisons.Among Double-Walled Carbon Nanotube(DWCNT)simulations,papers including the van der Waals interaction between the two cylinders are of particular interest.Aydogdu(2008)investigated free vibration of simply supported DWCNTs by using the parabolic shear deformation theory(PSDT).It was concluded that van der Waals(vdW)forces should be considered for small inner radius.Khosrozadeh and Hajabasi(2012)used the nonlocal Euler-Bernoulli beam theory to investigate nonlinear free vibration of DWCNTs.The interlayer vdW force was modelled as a nonlinear function of inner and outer tubes deflections.The nonlinear equations of motion of the DWCNTs derived by using the Euler beam theory and the Hamilton principle and the nonlinear van der Waals forces were considered in Fang et al.(2013).Natsuki et al.(2008)analyzed the vibration characteristics of simply supported DWCNTs by using Euler-Bernoulli beam theory and coupling the two nanotube shells through the van der Waals interaction.Equations of motion of elastically supported DWCNTs were established in Kianim(2013)using nonlocal Rayleigh,Timoshenko,and higher-order beam theories.The two tubes were appropriately interacted through consideration of interlayer van der Waals forces via an equivalent spring system.The effect of various parameters like the radius of nanotubes,van der Waals forces and nonlocal parameters on the longitudinal wave propagation in multiwalled carbon nanotubes was discussed in Aydogdu(2014).The influence of van der Waals interaction coefficient on the vibrational properties of DWCNTs was studied in de Borbón and Ambrosini(2012).A high order continuum beam model was used.Chang(2013)adopted stochastic FEM to study the statistical dynamic behaviors of nonlinear vibration of the fluid-conveying DWCNTs under a moving load by considering the effects of the geometric nonlinearity and the nonlinearity of van der Waals forces.Benguediab et al.(2014)studied the mechanical buckling properties of a zigzag double-walled carbon nanotube(DWCNT)with both chirality and small scale effects.

The use of shell models for the vibration analysis of CNTs is usually more complicated than the use of beam models,but shell models allow the analysis of CNTs with small length/diameter ratios.For these structures the use of 1D beam models gives significant errors because short CNTs are not one-dimensional structures.Re fined 2D or 3D shell models are suitable for the correct vibration analysis of short CNTs,in particular when the radius/thickness ratio is small,as demonstrated in Brischetto(2014a)and in Cinefra et al.(2011).The present author has proposed a continuum approach[Brischetto(2014a)](based on an exact elastic threedimensional shell model)for natural frequency investigation of simply supported Single-Walled Carbon Nanotubes(SWCNTs).Among SWCNT shell simulations,Wang and Zhang(2008b)proposed a two-dimensional elastic shell model to characterize the deformation of SWCNTs using the in-plane rigidity,Poisson ratio,bending rigidity and off-plane torsion rigidity as independent elastic constants.An elastic shell model of single-walled carbon nanotubes can be established only with a well-defined effective thickness.Vibrations of SWCNTs based on a threedimensional theory of elasticity were analyzed in Alibeigloo and Shaban(2013).The Flügge type shell equations were used in Mikhasev(2013)as governing equations for free axisymmetric vibrations of a SWCNT.Among DWCNT shell simulations,Cinefra et al.(2011)proposed re fined layer-wise 2D shell models which account for van der Waals(vdW)interaction between the inner and the outer cylinder.In general,vdW interaction gives a small decrease in the frequency value for the free vibration analysis.Dong et al.(2008)presented an analytical laminated cylindrical shell method to investigate wave propagation in individual multiwall carbon nanotubes(MWNTs)or MWNTs embedded in an elastic matrix.Further shell models for Double-Walled Carbon NanoTubes(DWCNTs)were proposed in Li and Kardomateas(2007)and in Yao and Han(2008)for free vibration and buckling analysis,respectively.For the analysis of MWNTs,He et al.(2005)have shown that the greatest contribution to the vdW interaction comes from the adjacent layers and the contribution from a remote layer may be negligible.Han et al.(2005)examined the instability of a DWCNT embedded in an elastic medium under pure bending.The effect of surrounding elastic medium and van der Waals forces between the inner and outer nanotubes was taken into consideration.Thermoelastic vibration and damping of a DWCNT upon interlayer van der Waals(vdW)interaction and initial axial stresses are studied in Hoseinzadeh and Khadem(2011).The inner and outer carbon nanotubes are modeled as two individual elastic thin shells.The present paper proposes an exact three-dimensional elastic shell model for free vibration analysis of simply supported DWCNTs.This work is an extension of the three-dimensional elastic shell model prosed by the same author for the free vibration analysis of SWCNTs[Brischetto(2014a)].The equilibrium equations in general orthogonal curvilinear coordinates(see Brischetto(2013),Brischetto(2014b),Brischetto(2014c)and Brischetto and Torre(2014))are adapted to the case of a cylinder by giving an in finite value for one of the two radii of curvature.The equilibrium equations in rectilinear orthogonal coordinates and in cylindrical coordinates were exactly solved in Messina(2009)and Soldatos and Ye(1995),respectively.In order to apply the 3D shell continuum model,DWCNTs are de fined as two concentric isotropic cylinders(with an equivalent thickness and Young modulus)which can be linked by means of the interlaminar continuity conditions( first model)or by means of an infinitesimal fictitious layer which represents the van der Waals interaction(second model).The comparisons between the two models show the effect of van der Waals interaction between the two cylinders for different Carbon NanoTube lengths and vibration modes.Results show the van der Waals interaction effect in terms of frequency values and the comparison between shell and beam models.

2 3D shell model

Multilayered spherical shells with constant radii of curvature Rαand Rβhave been analyzed in Brischetto(2013)and Brischetto(2014b)by means of three differential equations of equilibrium in general orthogonal curvilinear coordinates written for the case of free vibration analysis.The equations have been solved in exact form in analogy with the method proposed in Messina(2009)and Soldatos and Ye(1995)for orthogonal rectilinear coordinates and cylindrical coordinates,respectively.In the present paper,the equations in general orthogonal curvilinear coordinates are simplified for the cylindrical case by imposing an in finite value for the radius of curvature Rβ(see Fig.1).The general form proposed in Brischetto(2013)and Brischetto(2014b)remains valid for both plate and constant radius shell geometries(spherical and cylindrical shells).

Figure 1:Notation,reference system and continuum approach for a Single-Walled Carbon NanoTube(SWCNT)and a Double-Walled Carbon NanoTube(DWCNT).

The strain-displacement relations of three-dimensional theory of elasticity in orthogonal curvilinear coordinates are written for the generic k layer of the multilayered cylindrical shell of Fig.1(the general form for spherical shells with constant radii of curvature Rαand Rβhas already been given in Brischetto(2013)and Brischetto(2014b)):

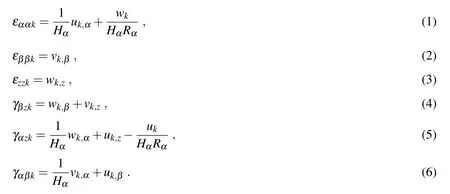
The parametric coefficients for cylindrical shells are:

Three-dimensional linear elastic constitutive equations in orthogonal curvilinear coordinates(α,β,z)(see Fig.1)are here given for a generic k isotropic layer.The stress componentsare linked with the strain componentsfor each k isotropic layer as:

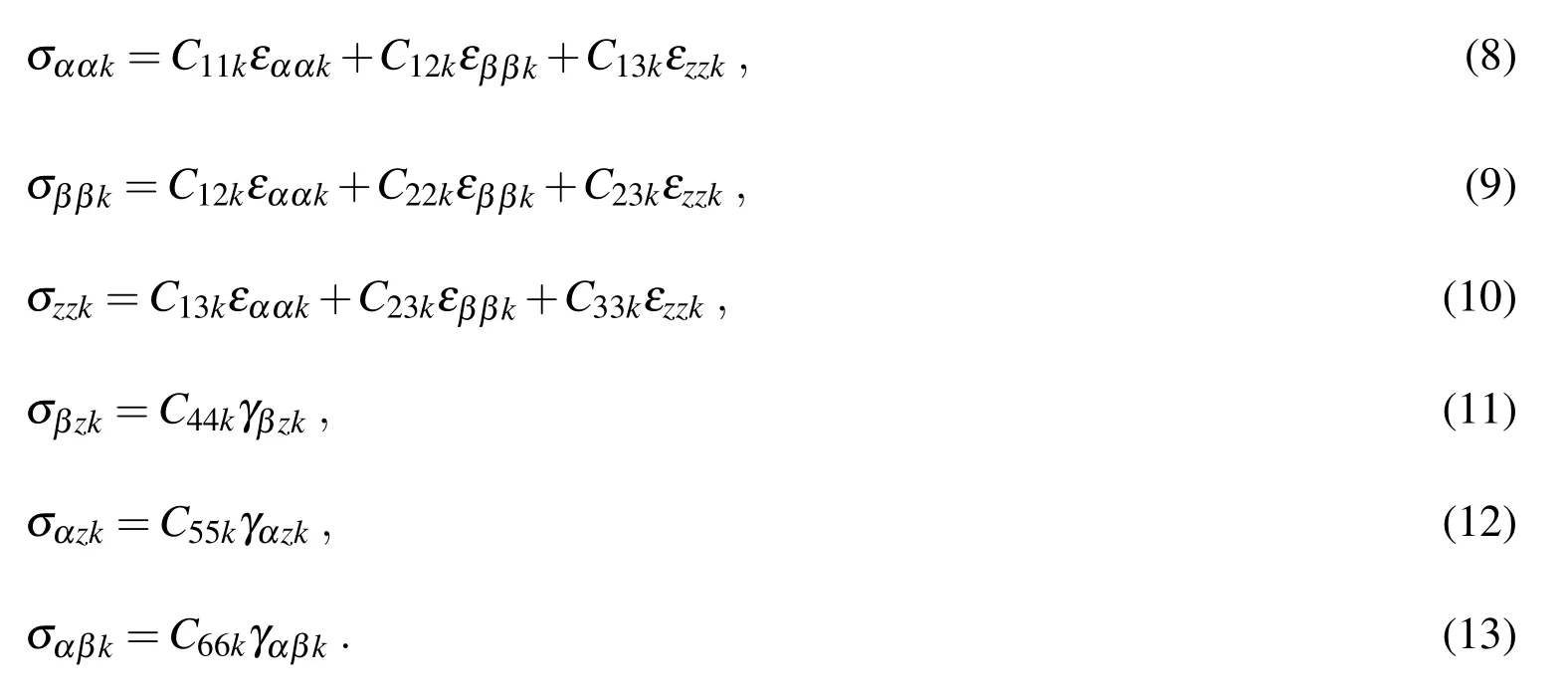
The most general form of differential equations of equilibrium for spherical shells with constant radii of curvature can be found in Brischetto(2013)and Brischetto(2014b).These equations rewritten for the case of free vibration analysis of cylindrical shells are:

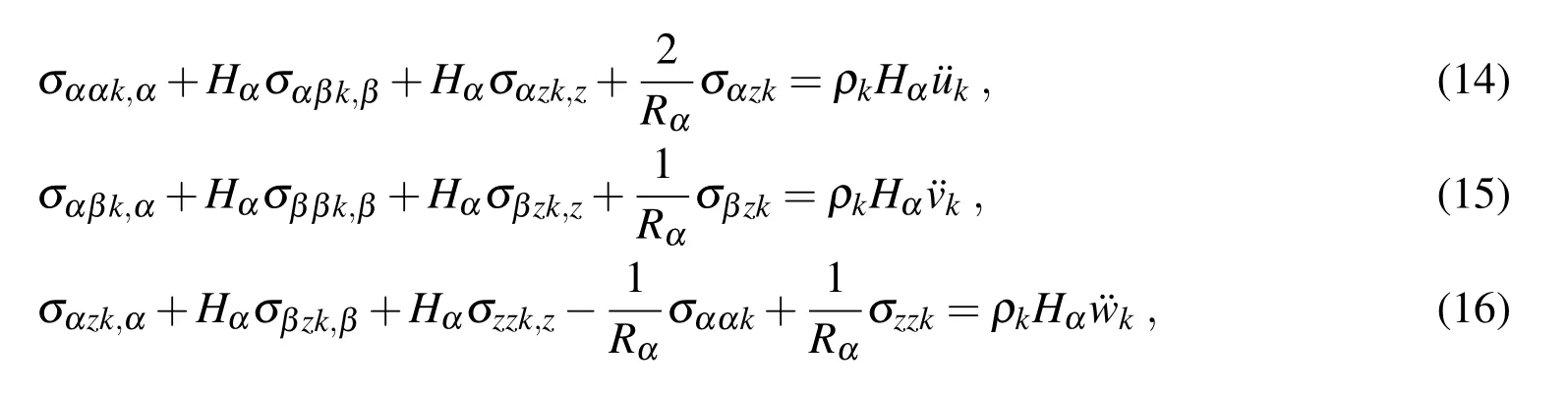
where ρkis the mass density.andindicate the second temporal derivative of the three displacement components uk,vkand wk,respectively.Each quantity depends on the k layer.Rαis referred to the mid-surface Ω0of the whole multilayered shell.Hαcontinuously varies through the thickness of the multilayered shell and it depends on the z thickness coordinate.Eqs.(14)-(16)have constant coefficients(even if a shell geometry is considered)when the shell is divided in NLmathematical layers where the parametric coefficient Hαcan easily be calculated in the middle of each k mathematical layer.

The closed form of Eqs.(14)-(16)is obtained for simply supported cylindrical shells.

The three displacement components have the following harmonic form:

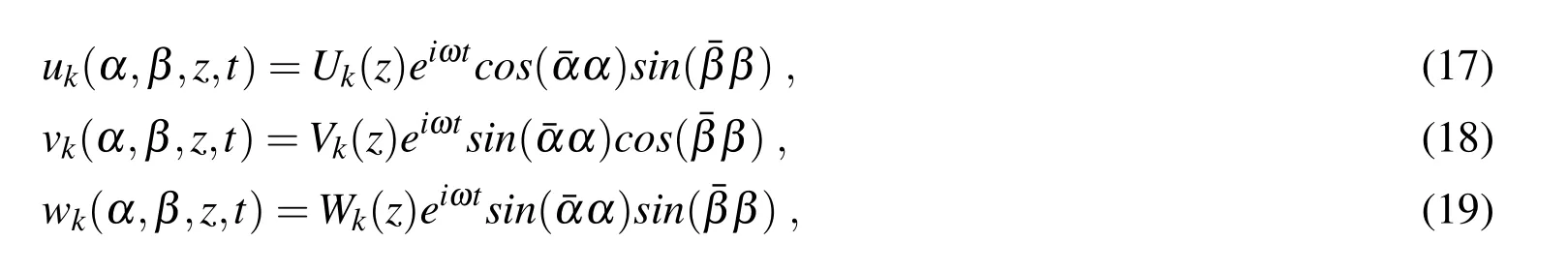
where Uk(z),Vk(z)and Wk(z)are the displacement amplitudes in α,β and z directions,respectively.i is the coefficient of the imaginary unit.is the circular frequency where f is the frequency value,t is the time.In coefficientsandp and q are the half-wave numbers and a and b are the shell dimensions in α and β directions,respectively(they are calculated in the reference mid-surface Ω0).

Eqs.(1)-(6),(8)-(13)and(17)-(19)are substituted in Eqs.(14)-(16)to obtain the following system of equations for each k mathematical layer:

Eqs.(23)-(25)are a system of three second order differential equations.This system can be reduced to a system of first order differential equations[Brischetto(2013);Brischetto(2014b);Messina(2009);Soldatos and Ye(1995)]:

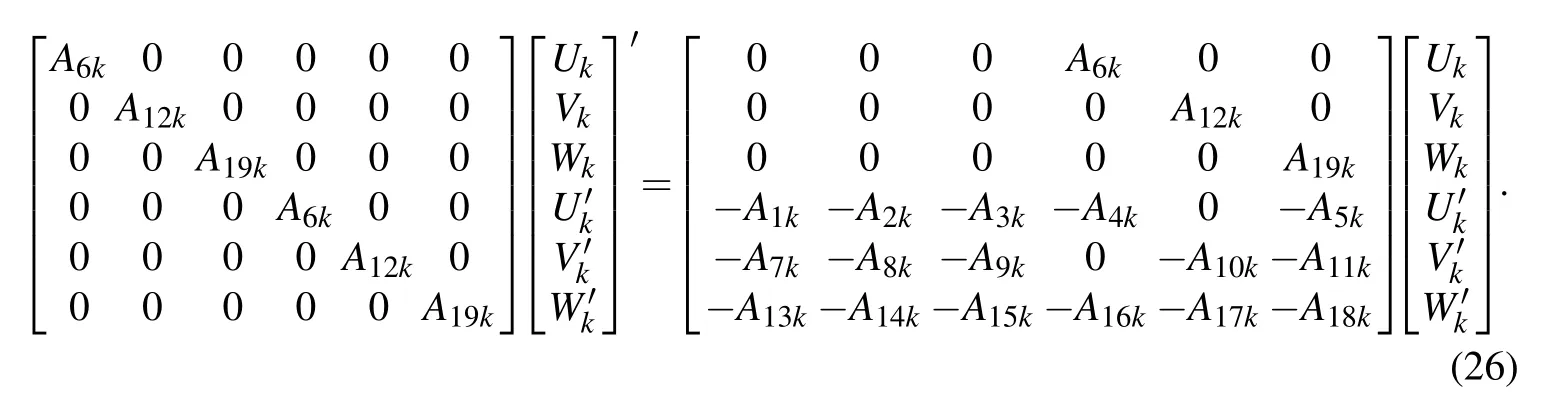
Eq.(26)can be written in a compact form for a generic k layer:

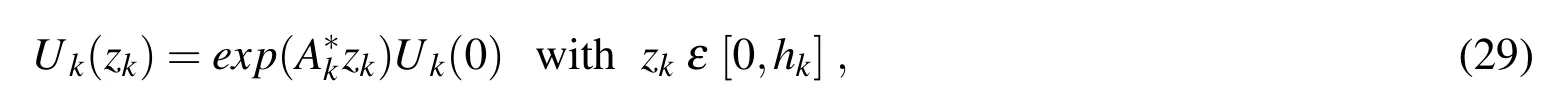
where zkis the thickness coordinate of each k layer from 0 at the bottom to hkat the top.

If we consider NLlayers,NL−1 transfer matrices Tk−1,kmust be calculated by using for each interface the following conditions for interlaminar continuity of displacements and transverse shear/normal stresses:

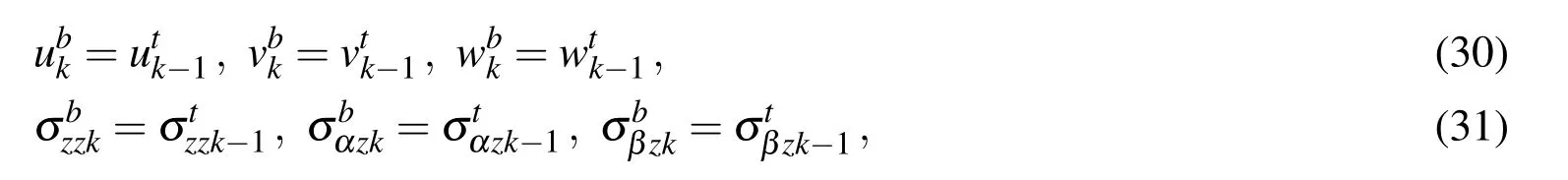
each displacement and transverse stress component at the top(t)of the k-1 layer is equal to each displacement and transverse stress component at the bottom(b)of the k layer.Eqs.(30)-(31)in compact form are:

The calculated Tk−1,kmatrices allow vector U at the bottom(b)of the k layer with vector U at the top(t)of the k−1 layer to be linked.The structures are simply supported and free stresses at the top and at the bottom,this feature means:

The combination of Eqs.(28),(29),(32)and(33)-(35)leads to the following system(details can be found in Brischetto(2013)and Brischetto(2014b)):

Matrix E has always(6×6)dimension,independently from the number NLof mathematical layers,even if the method uses a layer-wise approach.The free vibration analysis means to find the non-trivial solution of(displacement at the bottom of the layer 1)in Eq.(36)by imposing the determinant of matrix E equals zero:

Eq.(37)means to find the roots of an higher order polynomial in λ = ω2.For each pair of half-wave numbers(p,q)a certain number of circular frequencies are obtained depending on the order N chosen for the exponential matrix in Eq.(29)and the number NLof mathematical layers.

2.1 Analysis of DWCNT without van der Waals interaction

The DWCNT is analyzed in this paper by means of an equivalent continuum model where the two cylinders have thickness values hiand he(see Figs.1 and 2).The first model considers NL=228 mathematical layers to correctly approximate the curvature of the shell.The first cylinder(with thickness hi)is divided into 114 mathematical layers(from k=1 to k=114)and the second cylinder(with thickness he)is also divided into 114 mathematical layers(from k=115 to k=228).Mathematical layers are linked by means of the interlaminar continuity conditions given in Eqs.(30)and(31).Such conditions are also used to link layer k=114 to layer k=115,in this way the two cylinders are linked by means of interlaminar continuity conditions.This model is indicated as the 3D model in the results proposed.

2.2 Analysis of DWCNT including van der Waals interaction

Figure 2:Continuum 3D shell model for DWCNT analysis.Interlaminar continuity between the two cylinders(3D model)and van der Waals interaction between the two cylinders(3DvdWmodel).

The second model proposed in this paper is called the 3DvdWmodel because it allows van der Waals interaction to be included in the 3D continuum shell model described in Section 2.The two cylinders have thickness values hiand he.The first cylinder is divided into 114 fictitious layers(from k=1 to k=114)and the second cylinder is also divided into 114 fictitious layers(from k=116 to k=229).An infinitesimal layer(k=115)is introduced between the two cylinders to simulate the van der Waals interaction(see Fig.2).This infinitesimal fictitious layer has a negligible thicknessand opportune elastic properties which represent the van der Waals interaction.Layers k=114 and k=115,and layers k=115 and k=116 are linked by means of the interlaminar continuity conditions given in Eqs.(30)and(31).The fictitious layer k=115 has mass density ρ=1.225kg/m3(air density).The Poisson ratio is the same used for the other layers.The van der Waals interaction coefficient c,estimated at the initial interlayer spacing can be given as:

or as:

see de Borbón and Ambrosini(2012)for further details.d=0.142nm is the length of C-C bond and 1erg=10−7Joule.This coefficient has values c1=6.19916683×1019N/m3or c2=9.918667×1019N/m3.Transverse displacements for CNT analysis have values in the order of 10−12m.Therefore,the equivalent Young modulii for the in finitesimal fictitious layer which simulates van der Waals interactions are E1=6.19916683×107Pa or E2=9.918667×107Pa,respectively.The threedimensional models including van der Waals interaction are called 3DvdW(c1)and 3DvdW(c2).

3 Results

Figure 3:Geometrical data for the equivalent continuum DWCNT.

The three-dimensional shell model proposed in this paper is firstly validated by means of a comparison with the Double Timoshenko Beam Model(DTBM)proposed in de Borbón and Ambrosini(2012).The DTBM investigates the free vibration analysis of simply-supported Double Walled Carbon Nanotubes(DWCNTs).The two concentric cylinders are linked by means of the van der Waals interactions.DTBM(c1)considers a van der Waals interaction coefficient as described in Eq.(38).DTBM(c2)considers a van der Waals interaction coefficient as described in Eq.(39).The DWCNT has two layers with the same equivalent thickness hi=he=0.35nm(see Figs.1-3).The equivalent elastic properties are Young modulus E=1TPa and Poisson ratio ν =0.25.The mass density is ρ =2300kg/m3.Four different DWCNT geometries are investigated(see Figs.1 and 3 for reference values).The first nanotube has a reference diameter for the inner cylinder di=0.7nm and a reference diameter for the external cylinder de=1.4nm.The mean radius of curvature for the DWCNT is Rα=di/2+hi/2=0.525nm;this value means dimension a=2πRα=3.298672286nm.The second nanotube has a reference diameter for the inner cylinder di=2.95nm and a reference diameter for the external cylinder de=3.65nm.The mean radius of curvature for the DWCNT is Rα=di/2+hi/2=1.65nm;this value means dimension a=2πRα=10.367256nm.The third nanotube has a reference diameter for the inner cylinder di=4.80nm and a reference diameter for the external cylinder de=5.50nm.The mean radius of curvature for the DWCNT is Rα=di/2+hi/2=2.575nm;this value means dimension a=2πRα=16.1792022nm.The fourth nanotube has a reference diameter for the inner cylinder di=7.0nm and a reference diam-eter for the external cylinder de=7.70nm.The mean radius of curvature for the DWCNT is Rα=di/2+hi/2=3.675nm;this value means dimension a=2πRα=23.090706nm.The four DWCNTs have an in finity radius of curvature in β direction.The lengths L=b considered in the β direction are obtained from L/de=5,10,15,30 and 50.Table 1 compares the proposed 3D shell model with the beam model DTBM proposed in de Borbón and Ambrosini(2012).The fundamental frequency f in GHz is given for half-wave numbers p=2 and q=1.The first threecolumns compare the DTBM and the 3D model which include a van der Waals interaction coefficient c1=6.19916683×1019N/m3.The second three columns compare the DTBM and the 3D model which include a van der Waals interaction coefficient c2=9.918667×1019N/m3.The last two columns show the 3D model without van der Waals interaction where the two cylinders are linked by means of the interlaminar continuity conditions.∆c1and∆c2values allow some important considerations.The difference between the beam model and the 3D shell model decreases when the length ratio L/deincreases.Therefore,for long nanotubes the beam model is similar to the 3D shell model.The difference between the beam model and the 3D shell model increases when the thickness ratio Rα/h increases(h=hi+he).Bigger Rα/h values mean cylinders with thin layers.As already discussed in de Borbón and Ambrosini(2012),DTBM has some problems of nu-merical instability for nanotube 3 with L/de=15(see the different values for∆c1and∆c2)and for nanotube 4 with L/de=15(see the omitted value for∆c2).Beam results for L/deequals 30 and 50 were not given in de Borbón and Ambrosini(2012).The use of c1or c2value does not give visible differences,for this reason the 3D shell model will use only the c2coefficient in Tables 2-5.∆3Dvalues in Table 1 show the van der Waals interaction effects.The frequency obtained via the 3D shell model considering the interlaminar continuity conditions between the two cylinders is bigger than the frequency obtained via the 3D shell model considering the van der Waals interaction.This difference is bigger for short cylinders(small L/devalues)and it decreases for longer cylinders(big L/devalues).Moreover,van der Waals effects are negligible for cylinders with thin layers(see nanotubes 2,3 and 4).

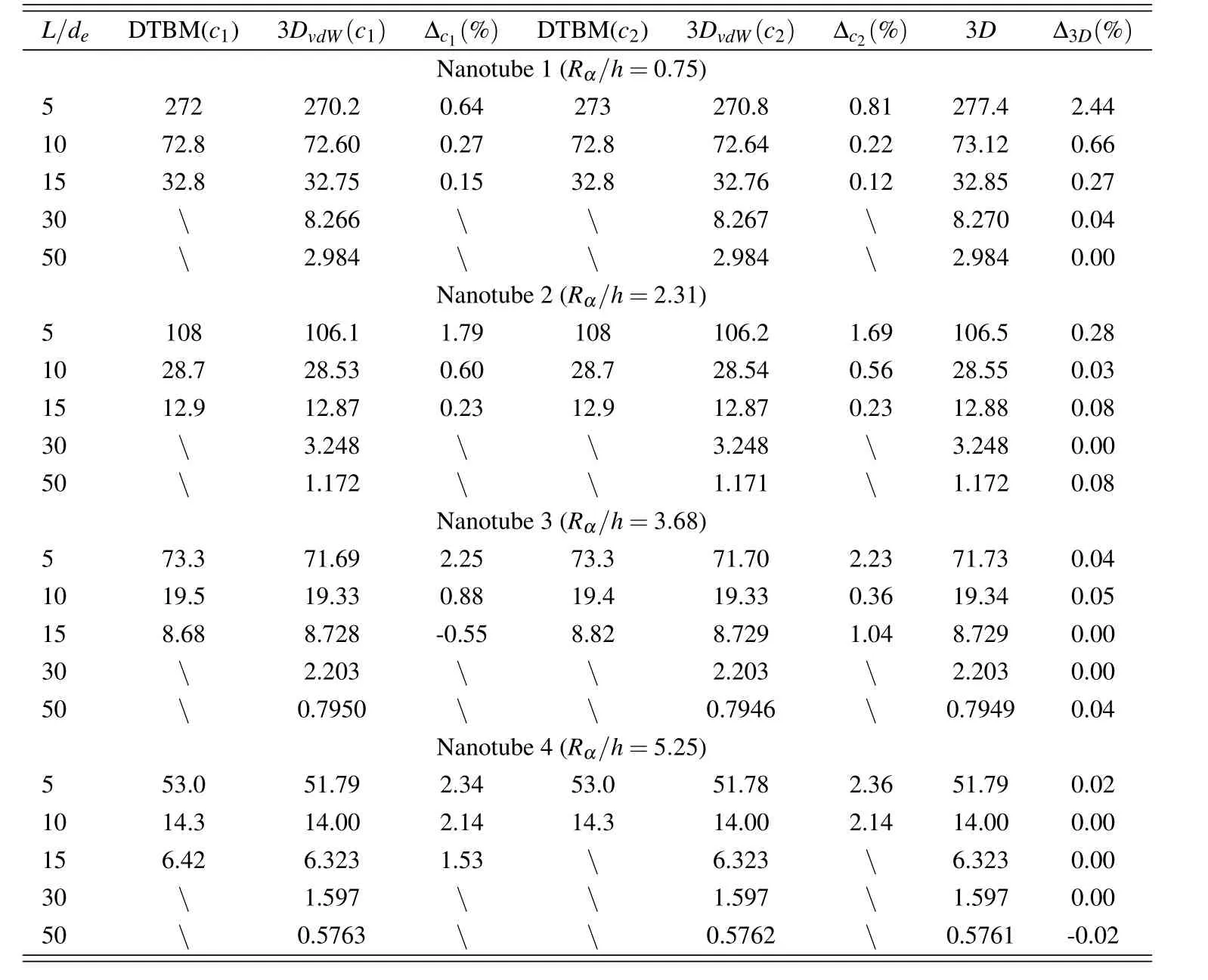
Table 1:Assessment.First natural frequency in GHz for half-wave numbers p=2 and q=1 and different L/deratios.DTBM is the Double Timoshenko Beam Model including van der Waals interaction as proposed in de Borbón and Ambrosini(2012).The beam effects are evaluated by means of100 and The van der Waals interaction effects are evaluated by means of

L/de DTBM(c1) 3DvdW(c1) ∆c1(%) DTBM(c2) 3DvdW(c2) ∆c2(%) 3D ∆3D(%)Nanotube 1(Rα/h=0.75)5 272 270.2 0.64 273 270.8 0.81 277.4 2.44 10 72.8 72.60 0.27 72.8 72.64 0.22 73.12 0.66 15 32.8 32.75 0.15 32.8 32.76 0.12 32.85 0.27 30 8.266 8.267 8.270 0.04 50 2.984 2.984 2.984 0.00 Nanotube 2(Rα/h=2.31)5 108 106.1 1.79 108 106.2 1.69 106.5 0.28 10 28.7 28.53 0.60 28.7 28.54 0.56 28.55 0.03 15 12.9 12.87 0.23 12.9 12.87 0.23 12.88 0.08 30 3.248 3.248 3.248 0.00 50 1.172 1.171 1.172 0.08 Nanotube 3(Rα/h=3.68)5 73.3 71.69 2.25 73.3 71.70 2.23 71.73 0.04 10 19.5 19.33 0.88 19.4 19.33 0.36 19.34 0.05 15 8.68 8.728 -0.55 8.82 8.729 1.04 8.729 0.00 30 2.203 2.203 2.203 0.00 50 0.7950 0.7946 0.7949 0.04 Nanotube 4(Rα/h=5.25)5 53.0 51.79 2.34 53.0 51.78 2.36 51.79 0.02 10 14.3 14.00 2.14 14.3 14.00 2.14 14.00 0.00 15 6.42 6.323 1.53 6.323 6.323 0.00 30 1.597 1.597 1.597 0.00 50 0.5763 0.5762 0.5761 -0.02

Table 2:Benchmark: first nanotube with thickness ratio Rα/h=0.75.Frequency values in GHz for different half-wave numbers(p,q)and L/deratios.The van der Waals effects are evaluated by means of

(p,q) 3D 3DvdW(c2) ∆vdW(%)L/de=5(2,1) 277.4 270.8 2.44(2,2) 947.3 892.3 6.16(2,3) 1813 1628 11.4 L/de=10(2,1) 73.12 72.64 0.66(2,2) 277.4 270.8 2.44(2,3) 579.5 554.3 4.55 L/de=15(2,1) 32.85 32.76 0.27(2,2) 128.1 126.6 1.18(2,3) 277.4 270.8 2.44 L/de=30(2,1) 8.270 8.267 0.04(2,2) 32.85 32.76 0.27(2,3) 73.12 72.64 0.66 L/de=50(2,1) 2.984 2.984 0.00(2,2) 11.89 11.89 0.00(2,3) 26.65 26.60 0.19

Table 3:Benchmark:second nanotube with thickness ratio Rα/h=2.31.Frequency values in GHz for different half-wave numbers(p,q)and L/deratios.The van der Waals effects are evaluated by means of

(p,q) 3D 3DvdW(c2) ∆vdW(%)L/de=5(2,1) 106.5 106.2 0.28(2,2) 347.9 346.1 0.52(2,3) 632.5 624.2 1.33 L/de=10(2,1) 28.55 28.54 0.03(2,2) 106.5 106.2 0.28(2,3) 217.6 216.7 0.41 L/de=15(2,1) 12.88 12.87 0.08(2,2) 49.79 49.74 0.10(2,3) 106.5 106.2 0.28 L/de=30(2,1) 3.248 3.248 0.00(2,2) 12.88 12.87 0.08(2,3) 28.55 28.53 0.07 L/de=50(2,1) 1.172 1.171 0.08(2,2) 4.671 4.671 0.00(2,3) 10.45 10.45 0.00

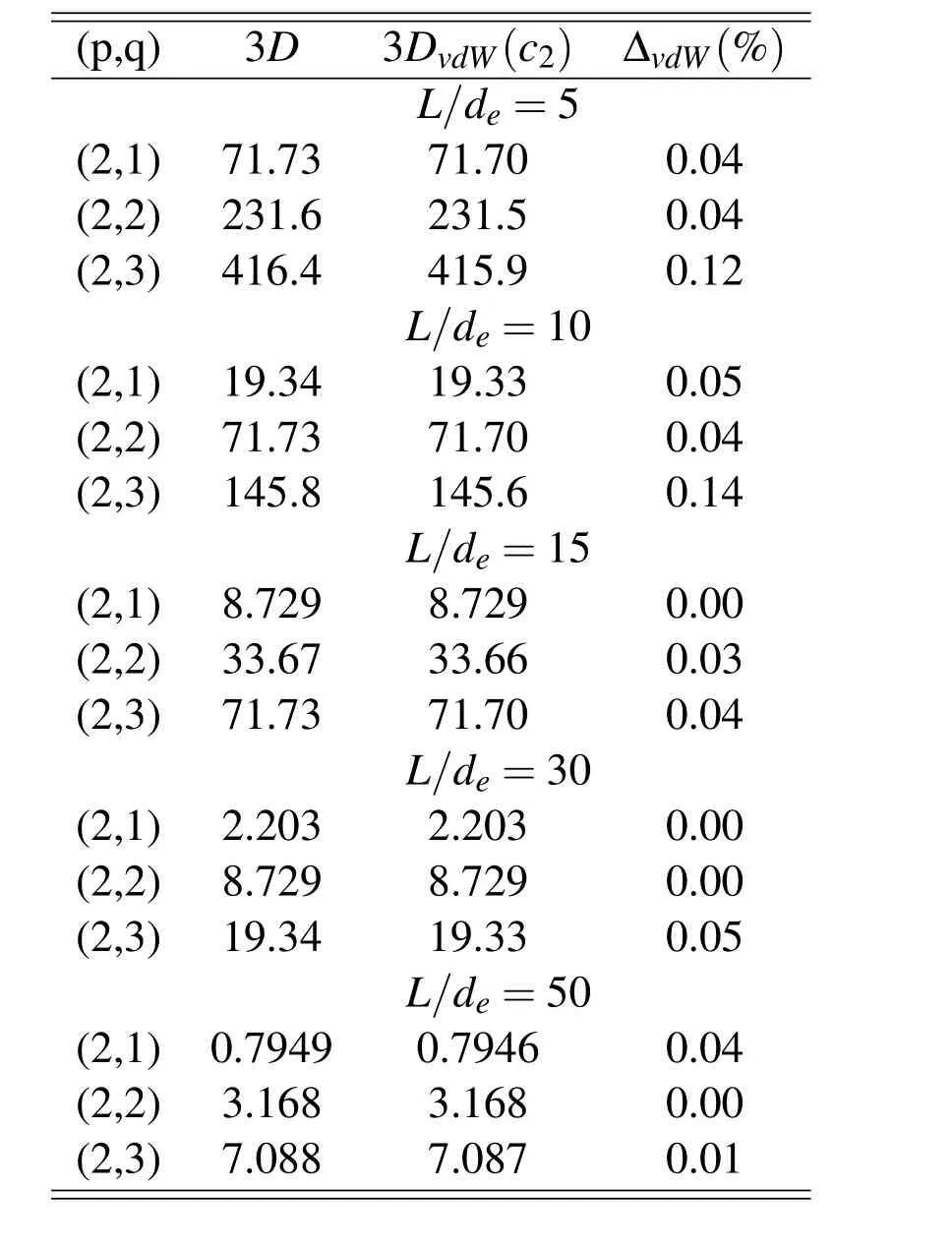
Table 4:Benchmark:third nanotube with thickness ratio Rα/h=3.68.Frequency values in GHz for different half-wave numbers(p,q)and L/deratios.The van der Waals effects are evaluated by means of

Tables 2-5 compare the 3D shell model including interlaminar continuity conditions with the 3D shell model including the van der Waals interaction(only the c2coefficient case is analyzed because Table 1 did not show significant differences for the use of c1and c2coefficient).The effect of the half-wave numbers(p,q)is also investigated in Tables 2-5.Table 2 considers a nanotube with thick layers for the two cylinders,in this case the van der Waals effect is important and it increases when the longitudinal half-wave number q increases.This effect decreases for long nanotubes(from L/de=5 to L/de=50).These considerations are also summarized in Fig.4,the van der Waals effect increases with the longitudinal half-wave number q value and it is more important for short cylinders(whereas it is negligible for long cylinders).Tables 3-5 consider nanotubes with thinner layers(Rα/h=2.31 for nanotube 2,Rα/h=3.68 for nanotube 3 and Rα/h=5.25 for nanotube 4).Inthese cases the van der Waals effect is less important and can be considered negligible for long cylinders(L/devalues greater than 15)even if higher longitudinal half-wave numbers q are imposed.

Table 5:Benchmark:fourth nanotube with thickness ratio Rα/h=5.25.Frequency values in GHz for different half-wave numbers(p,q)and L/deratios.The van der Waals effects are evaluated by means of

4 Conclusions

The free vibration analysis of simply supported Double-Walled Carbon NanoTubes(DWCNTs)is here proposed by means of a continuum 3D shell model.The layerwise approach of the model allows interlaminar continuity or van der Waals interaction conditions to be imposed between the two concentric cylinders.This feature allows the evaluation of the van der Waals interaction effect in free vibration analysis of DWCNTs.This effect is important and cannot be discarded for short nan-otubes,higher values of half-wave numbers imposed and/or thick cylinders.In all the other cases van der Waals interaction can be considered negligible.Moreover,a comparison between the present 3D shell model and a Timoshenko beam model already present in the literature has also been proposed.The beam model remains valid for long DWCNTs and/or thick layers for the cylinders.For short DWCNTs and/or thin layers for the cylinders,the use of the 3D shell model is mandatory.

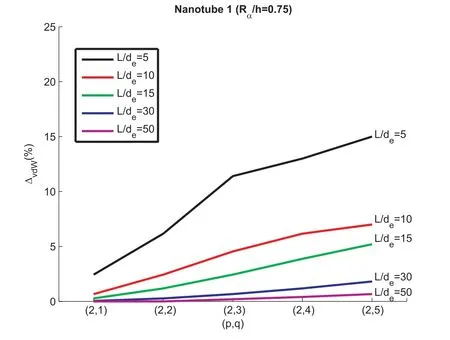
Figure 4:First nanotube with thickness ratio Rα/h=0.75:van der Waals force interaction effects versus half-wave numbers(p,q)and CNT lengths(L/deratios).

Bibliography

Alibeigloo,A.;Shaban,M.(2013):Free vibration analysis of carbon nanotubes by using three-dimensional theory of elasticity.Acta Mechanica,vol.224,pp.1415-1427.

Ansari,R.;Ajori,S.;Arash,B.(2012):Vibrations of single-and double-walled carbon nanotubes with layerwise boundary conditions:A molecular dynamics study.Current Applied Physics,vol.12,pp.707-711.

Araújo dos Santos,J.V.(2011):Effective elastic moduli evaluation of single walled carbon nanotubes using flexural vibrations.Mechanics of Advanced Materials and Structures,vol.18,pp.262-271.

Arghavan,S.;Singh,A.V.(2011):On the vibrations of single-walled carbon nanotubes.Journal of Sound and Vibration,vol.330,pp.3102-3122.

Aydogdu,M.(2008):Vibration of multi-walled carbon nanotubes by generalized shear deformation theory.International Journal of Mechanical Sciences,vol.50,pp.837-844.

Aydogdu,M.(2009a):Axial vibration of the nanorods with the non local continuum rod model.Physica E,vol.41,pp.861-864.

Aydogdu,M.(2009b):A general non local beam theory:Its application to nanobeam bending,buckling and vibration.Physica E,vol.41,pp.1651-1655.

Aydogdu,M.(2014):Longitudinal wave propagation in multiwalled carbon nanotubes.Composite Structures,vol.107,pp.578-584.

Azrar,A.;Azrar,L.;Aljinaidi,A.A.(2011):Length scale effect analysis on vibration behavior of single walled carbon nanotubes with arbitrary boundary conditions.Revue de Mécanique Appliquée et Théorique,vol.2,pp.475-485.

Benguediab,S.;Tounsi,A.;Zidour,M.;Semmah,A.(2014):Chirality and scale effects on mechanical buckling properties of zigzag double-walled carbon nanotubes.Composites:Part B,vol.57,pp.21-24.

Benzair,A.;Tounsi,A.;Besseghier,A.;Heireche,H.;Moulay,N.;Boumia,L.(2008):The thermal effect on vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory.Journal of Physics D:Applied Physics,vol.41,pp.1-10.

Brenner,D.W.;Shenderova,O.A.;Areshkin,D.A.;Schall,J.D.;Frankland,S.J.V.(2002):Atomic modeling of carbon-based nanostructures as a tool for developing new materials and technologies.CMES:Computer Modeling in Engineering&Sciences,vol.3,pp.643-674.

Brischetto,S.(2013):Exact elasticity solution for natural frequencies of functionally graded simply-supported structures.CMES:Computer Modeling in Engineering&Sciences,vol.95,pp.391-430.

Brischetto,S.(2014a):A continuum elastic three-dimensional model for natural frequencies of single-walled carbon nanotubes.Composites:Part B,vol.61,pp.222-228.

Brischetto,S.(2014b):Three-dimensional exact free vibration analysis of spherical,cylindrical and flat one-layered panels.Shock and Vibration,vol.2014,pp.1-29.

Brischetto,S.(2014c):An exact 3D solution for free vibrations of multilayered cross-ply composite and sandwich plates and shells.International Journal of Applied Mechanics,vol.6,pp.1-42.

Brischetto,S.;Torre,R.(2014):Exact 3D solutions and finite element 2D models for free vibration analysis of plates and cylinders.Curved and Layered Structures,vol.1,pp.59-92.

Chang,T.P.(2013):Stochastic FEM on nonlinear vibration of fluid-loaded doublewalled carbon nanotubes subjected to a moving load based on nonlocal elasticity theory.Composites:Part B,vol.54,pp.391-399.

Chen,X.;Cao,G.(2006):A structural mechanics study of single-walled carbon nanotubes generalized from atomistic simulation.Nanotechnology,vol.17,pp.1004-1015.

Chowdhury,R.;Adhikari,S.;Wang,C.Y.;Scarpa,F.(2010):A molecular mechanics approach for the vibration of single-walled carbon nanotubes.Computational Materials Science,vol.48,pp.730-735.

Cinefra,M.;Carrera,E.;Brischetto,S.(2011):Re fined shell models for the vibration analysis of multiwalled carbon nanotubes.Mechanics of Advanced Materials and Structures,vol.18,pp.476-483.

Das,S.L.;Mandal,T.;Gupta,S.S.(2013):Inextensional vibration of zig-zag single-walled carbon nanotubes using nonlocal elasticity theories.International Journal of Solids and Structures,vol.50,pp.2792-2797.

de Borbón,F.;Ambrosini,D.(2012):On the influence of van der Waals coefficient on the transverse vibration of double walled carbon nanotubes.Computational Materials Science,vol.65,pp.504-508.

Demir,C.;Civalek,O.;Akgöz,B.(2010):Free vibration analysis of carbon nanotubes based on shear deformable beam theory by discrete singular convolution technique.Mathematical and Computational Applications,vol.15,pp.57-65.

Dong,K.;Zhu,S.Q.;Wang,X.(2008):Wave propagation in multiwall carbon nanotubes embedded in a matrix material.Composite Structures,vol.82,pp.1-9.

Fang,B.;Zhen,Y.X.;Zhang,C.P.;Tang,Y.(2013):Nonlinear vibration analysis of double-walled carbon nanotubes based on nonlocal elasticity theory.Applied Mathematical Modelling,vol.37,pp.1096-1107.

Foda,M.A.(2013):Steady state vibration analysis and mitigation of single-walled carbon nanotubes based on nonlocal Timoshenko beam theory.Computational Materials Science,vol.71,pp.38-46.

Ghouhestani,S.;Shahabian,F.;Hosseini,S.M.(2014):Dynamic analysis of a layered cylinder reinforced by functionally graded carbon nanotubes distributions subjected to shock loading using MLPG method.CMES:Computer Modeling in Engineering&Sciences,vol.100,pp.295-321.

Gupta,A.;Sharma,S.C.;Harsha,S.P.(2012):Vibration analysis of carbon nanotubes based mass sensor using different boundary conditions.International Journal of Mechanical Sciences,vol.2,pp.8-12.

Han,Q.;Lu,G.;Dai,L.(2005):Bending instability of an embedded doublewalled carbon nanotube based on Winkler and van der Waals models.Composites Science and Technology,vol.65,pp.1337-1346.

He,X.Q.;Kitipornchai,S.;Wang,C.M.;Liew,K.M.(2005):Modeling of van der Waals force for in finitesimal deformation of multi-walled carbon nanotubes treated as cylindrical shells.International Journal of Solids and Structures,vol.42,pp.6032-6047.

Horng,T.L.(2012):Transverse vibration analysis of single-walled carbon nanotubes embedded in an elastic medium using Bernoulli-Fourier method.Journal of Surface Engineered Materials and Advanced Technology,vol.2,pp.203-209.

Hoseinzadeh,M.S.;Khadem,S.E.(2011):Thermoelastic vibration and damping analysis of double-walled carbon nanotubes based on shell theory.Physica E,vol.43,pp.1146-1154.

Hu,Y.G.;Liew,K.M.;Wang,Q.(2012):Modeling of vibrations of carbon nanotubes.Procedia Engineering,vol.31,pp.343-347.

Iijima,S.(1991):Helical microtubules of graphitic carbon.Nature,vol.354,pp.56-58.

Khosrozadeh,A.;Hajabasi,M.A.(2012):Free vibration of embedded doublewalled carbon nanotubes considering nonlinear interlayer van der Waals forces.Applied Mathematical Modelling,vol.36,pp.997-1007.

Kiani,K.(2013):Vibration analysis of elastically restrained double-walled carbon nanotubes on elastic foundation subjected to axial load using nonlocal shear deformable beam theories.International Journal of Mechanical Sciences,vol.68,pp.16-34.

Lee,U.;Oh,H.(2008):Evaluation of the structural properties of single-walled carbon nanotubes using a dynamic continuum modeling method.Mechanics of Advanced Materials and Structures,vol.15,pp.79-87.

Li,R.;Kardomateas,G.A.(2007):Vibration characteristics of multiwalled carbon nanotubes embedded in elastic media by a nonlocal elastic shell model.Journal of Applied Mechanics,vol.74,pp.1087-1094.

Messina,A.(2009):Three Dimensional Free Vibration Analysis of Cross-Ply Laminated Plates through 2D and Exact Models.3rd International Conference on Integrity,Reliability and Failure,Porto(Portugal).

Mikhasev,M.(2013):On localized modes of free vibrations of single-walled carbon nanotubes embedded in nonhomogeneous elastic medium. Zeitschrift für Angewandte Mathematik und Mechanik,pp.1-12.

Ming,L.;Huiming,Z.(2013):Small scale effect on thermal vibration of singlewalled carbon nanotubes with nonlocal boundary condition.Research Journal of Applied Sciences,Engineering and Technology,vol.5,pp.2729-2733.

Mir,M.;Hosseini,A.;Majzoobi,G.H.(2008):A numerical study of vibrational properties of single-walled carbon nanotubes.Computational Materials Science,vol.43,pp.540-548.

Murmu,T.;Pradhan,S.C.(2009):Buckling analysis of a single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity and Timoshenko beam theory and using DQM.Physica E,vol.41,pp.1232-1239.

Namilae,S.;Chandra,U.;Srinivasan,A.;Chandra,N.(2007):Effect of inter-face modification on the mechanical behavior of carbon nanotube reinforced composites using parallel molecular dynamics simulations.CMES:Computer Modeling in Engineering&Sciences,vol.22,pp.189-202.

Natsuki,T.;Ni,Q.Q.;Endo,M.(2008):Analysis of the vibration characteristics of double-walled carbon nanotubes.Carbon,vol.46,pp.1570-1573.

Odegard G.M.;Gates T.S.;Nicholson L.M.;Wise K.E.(2002):Equivalentcontinuum modeling of nano-structured materials.Composites Science and Technology,vol.62,pp.1869-1880.

Qian,D.;Wagner,G.J.;Liu,W.K.;Yu,M.F.;Ruoff,R.S.(2002):Mechanics of carbon nanotubes.Applied Mechanics Reviews,vol.55,pp.495-533.

Rouainia,G.;Djeghaba,K.(2008):Evaluation of Young’s modulus of single walled carbon nanotube(SWNT)reinforced concrete composite.Journal of Engineering and Applied Science,vol.3,pp.504-515.

Soldatos,K.P.;Ye,J.(1995):Axisymmetric static and dynamic analysis of laminated hollow cylinders composed of monoclinic elastic layers.Journal of Sound and Vibration,vol.184,pp.245-259.

Simsek,M.(2010):Vibration analysis of a single-walled carbon nanotube under action of a moving harmonic load based on nonlocal elasticity theory.Physica E,vol.43,pp.182-191.

Sinnott,S.S.;Mao,Z.;Lee,K.H.(2002):Computational studies of molecular diffusion through carbon nanotube based membranes.CMES:Computer Modeling in Engineering&Sciences,vol.3,pp.589-600.

Soltani,P.;Kassaei,A.;Taherian,M.M.;Farshidianfar,A.(2012):Vibration of wavy single-walled carbon nanotubes based on nonlocal Euler Bernoulli and Timoshenko models.International Journal of Advanced Structural Engineering,vol.4,pp.1-10.

Srivastava,D.;Atluri,S.N.(2002):Computational nanotechnology:a current perspective.CMES:Computer Modeling in Engineering&Sciences,vol.3,pp.531-538.

Swain,A.;Roy,T.;Nanda,P.K.(2013):Vibration behaviour of single walled carbon nanotube using finite element. International Journal on Theoretical and Applied Research in Mechanical Engineering,vol.2,pp.129-133.

Valavala,P.K.;Odegard,G.M.(2005):Modeling techniques for determination of mechanical properties of polymer nanocomposites.Reviews on Advanced Materials Science,vol.9,pp.34-44.

Vodenitcharova,T.;Zhang,L.C.(2003):Effective wall thickness of a singlewalled carbon nanotube.Physical Review B,vol.68,pp.1-4.

Wang,B.;Deng,Z.C.;Zhang,K.(2013):Nonlinear vibration of embedded single-walled carbon nanotube with geometrical imperfection under harmonic load based on nonlocal Timoshenko beam theory.Applied Mathematics and Mechanics,vol.34,pp.269-280.

Wang,B.L.;Wang,K.F.(2013):Vibration analysis of embedded nanotubes using nonlocal continuum theory.Composites:Part B,vol.47,pp.96-101.

Wang,C.Y.;Zhang L.C.(2008a):A critical assessment of the elastic properties and effective wall thickness of single-walled carbon nanotubes.Nanotechnology,vol.19,pp.1-5.

Wang,C.Y.;Zhang,L.C.(2008b):An elastic shell model for characterizing single-walled carbon nanotubes.Nanotechnology,vol.19,pp.1-6.

Wu,C.P.;Jiang,R.Y.(2014):A state space differential reproducing kernel method for the buckling analysis of carbon nanotube-reinforced composite circular hollow cylinders.CMES:Computer Modeling in Engineering&Sciences,vol.97,pp.239-279.

Yan,J.W.;Liew,K.M.;He,L.H.(2013):Free vibration analysis of singlewalled carbon nanotubes using a higher-order gradient theory.Journal of Sound and Vibration,vol.332,pp.3740-3755.

Yan,Y.;Shi,G.;Zhao,P.(2011):Frequency study of single-walled carbon nanotubes based on a space-frame model with flexible connections.Journal of Computers,vol.6,pp.1125-1130.

Yang,L.;Han,J.;Anantram,M.P.;Jaffe,R.L.(2002):Bonding geometry and bandgap changes of carbon nanotubes under uniaxial and torsional strain.CMES:Computer Modeling in Engineering&Sciences,vol.3,pp.675-686.

Yao,X.;Han,Q.(2008):Torsional buckling and postbuckling equilibrium path of double-walled carbon nanotubes.Composites Science and Technology,vol.68,pp.113-120.

Zhang,L.C.(2009):On the mechanics of single-walled carbon nanotubes.Journal of Materials Processing Technology,vol.209,pp.4223-4228.

Zhang,Y.Y.;Wang,C.M.;Tan,V.B.C.(2009):Assessment of Timoshenko beam models for vibrational behavior of single-walled carbon nanotubes using molecular dynamics.Advances in Applied Mathematics and Mechanics,vol.1,pp.89-106.

1Corresponding author:Salvatore Brischetto,Department of Mechanical and Aerospace Engineering,Politecnico di Torino,Corso Duca degli Abruzzi,24,10129 Torino,ITALY.Tel:+39.011.090.6813;Fax:+39.011.090.6899;E-mail:salvatore.brischetto@polito.it.

Computer Modeling In Engineering&Sciences2015年4期

Computer Modeling In Engineering&Sciences的其它文章: A High-order Coupled Compact Integrated RBF Approximation Based Domain Decomposition Algorithm for Second-order Differential Problems; The Lie-group Shooting Method for Radial Symmetric Solutions of the Yamabe Equation