Effects of Geometry and Shape on the Mechanical Behaviors of Silicon Nanowires
Qunfeng Liu,Liang Wangand Shengping Shen
Effects of Geometry and Shape on the Mechanical Behaviors of Silicon Nanowires
Qunfeng Liu1,2,Liang Wang1and Shengping Shen1
Molecular dynamics simulations have been performed to investigate the effects of cross section geometry and shape on the mechanical behaviors of silicon nanowires(Si NWs)under tensile loading.The results show that elasticity of<100>rectangular Si NWs depends on their cross section aspect ratios while the elastic limits of<110>and<111>wires show geometry independence.Despite the significant influence of axial orientation,both yield stress and Young’s Modulus show the remarkable shape dependence for wires with various regular cross sections.Additionally,underlying mechanism for the geometry and shape effects on mechanical behavior are discussed based on the fundamental energy theory.From energy view,edge energy is the crucial factor that determines shape dependence of the elastic limits.
Silicon nanowire,Cross section,Geometry effect,Shape effect,Elastic limits.
1 Introduction
Silicon nanowires(Si NWs)have been considered as fundamental building blocks in the future nano-electro-mechanical systems(NEMS)[Cui et al.(2003)]and have been extensively investigated due to their unique mechanical,electric,optoelectronic and thermal properties[Shir et al.(2006);Jin et al.(2007);Donadio and Galli(2010);Sivakov et al.(2010);Sohn et al.(2010)].These interesting physical properties in Si NWs proved to result from their high surface-to-volume ratios that are quite different from those of bulk silicon.Since surface atoms with uncoordinated lattice structures behave distinctively from that of fully coordinated interior atoms,nanowires subjected to external loading will undergo a unique mechanical behaviors during the deformation process[Sohn et al.(2010)].Furthermore,thestability of the physical properties of Si NWs is related to the robustness of mechanical properties determined by large proportional surface atoms.Thus,investigations on the mechanical behaviors of SiNWs are crucial for future engineering applications.
Experiments have reported that Si NWs can be synthesized in different cross section shapes,geometries and axial orientations with respect to different synthesis methods[Shi et al.(2000);Bandaru and Pichanusakorn(2010)].By varying temperatures,the geometry of nanomaterials can be rectified artificially to obtain some modified physical and mechanical properties[Qu et al.(2004);Qian et al.(2008)].For ZnO nanobelts,the Young’s modulus was observed to depend strongly on the aspect ratio of their cross sections[Lucas et al.(2007)].It was reported that metal nano-particles with different cross section geometries have different optical properties[Mclaren et al.(2009)].Besides,cross-sectional shape effect plays a significant role in determining mechanical properties of nanostructures[Cao and Ma(2008);Sohn et al.(2010)].The structural,electrical,optical and magnetic properties of ZnO nanowires can be profoundly modulated by altering their cross-sectional shapes[Qu et al.(2004);Qian et al.(2008)].This shape effect on the mechanical properties of nanowires has also been investigated by some molecular dynamics simulations[Ji and Park(2006);Yang et al.(2009)].The results demonstrated that transverse shape and geometry affect the mechanical properties of nanowires in a different way.However,the underlying mechanism of both effects on the mechanical behavior and yield responses are limited.
In previous researches,mechanical properties of silicon nanowires have been intensively studied,particularly on the wires with square or circular cross sections[Yang et al.(2009);Sohn et al.(2010)].Little work has been done on wires with other cross section shapes,even though they are energetically favorable during synthesis process.In essence,regular cross sections are composed of surfaces and edges.Thus,effects of geometry and shape can be considered as the combined effects of intrinsic surfaces and edges.Therefore,by studying the surface and edge effects,we can provide a general understanding of the combined effects of cross section geometry,shape,as well as axial orientation on the mechanical behavior of Si NWs.This can not only explain the geometry and shape effects in a generic sense,but can provide alternative ways for engineering the mechanical properties of Si NWs as well.
In this work,we firstly describe the simulation methodology and the fundamental energy based mechanics used to analyze the mechanical behaviors of the SiNWs.Then we employ molecular dynamics(MD)simulations to investigate the effect of cross section geometry on the elastic limits of silicon nanowires with different axial orientations.The influence of cross section shape on the elasticity is also studied according to the correlation between mechanical behaviors and their cross sections.Finally,we discuss the underlying mechanism of the mechanical behaviors by comparing the influential factors between geometry effect and shape effect.
2 Methodology
According to the fundamental energy based mechanics approach[Shuttleworth(1950);Zhang et al.(2008)],the total potential energy of a nanowire can be regarded to be the sum of bulk energies,surface energies,and edge energies.For the initial nanowire model,the total potential energy Utcan be expressed by

where U0is the reference energy of the strain-free bulk counterpart,are the initial surface energy and edge energy,respectively.In this work,we first statically relaxed the nanowires with free boundaries,which can effectively diminish the initial residual surface stress and cause an initial strain along axial orientation.After static relaxation,all wires were dynamically equilibrated with two ends fixed in NVT and NVE ensembles,leading to a minimized total potential energy.Thus,the total system energy can be simplified as

whereUexc=Us+Ueis the total excess energy due to surface energy(Us)and edge energy(Ue)of wire at equilibrium;Ub=U0+is the total bulk energy arising from the nonlinear elasticity[Liang et al.(2005)]within the nanowire core due to the relaxation of excess energy,whereis the introduced equilibrium strain energy.Particularly,if wire cross section is regular polygon,which comprises k edges and k facets,the total excess energy per unit length U¯exccan be calculated from

where γiis the surface energy per unit area,liis the facet length on the cross section of the i−th facet,and ηiis the edge energy per unit length of the i−th edge.
Previous researches demonstrated that the size dependence of elastic Young’s modulus in nanowires[Diao et al.(2004);Liang et al.(2005);Zhang et al.(2008)]was primarily due to the relaxation of the total system energy.Under a uniaxial loading,wires are stretched by a strain increment in the NVE ensemble.The total potential energy Utis given by

where W is the work done by the applied strain ε.The effective Young’s modulus E can be expressed as the second derivative of the strain energy with respect to the applied strain,

where V is the instantaneous volume of wire.The volume change due to lateral Poisson’s effect can be negligible during the first elastic deformation stage,where W can be expressed as 1/2Eεε2and the second derivative of W is a constant Eε.Besides,bulk strain energy Ubdue to surface effect can be considered as an extra contribution to the wire core energy induced by surface excess energiesUexc.Thus,according to equations(4)and(5),it was concluded that the elastic properties of nanowires are determined not only by the bulk strain energy of hypothetical wire,but also by their surface and edge energies which differ with their cross section geometries and shapes.
To calculate bulk strain energy,both continuum method[Huang et al.(2013);Joseph and Lu(2014)]and atomistic method can be utilized;while for surface and edge energies calculation,atomistic simulation has the merit to descript the surface deformation details based on their atomic coordinates.Thus,we performed molecular dynamics simulations with a MEAM potential for Si-Si interactions to study the uniaxial tensile deformation behaviors of Si NWs.The empirical MEAM potential was developed by Maria and Thijsse[Timonova and Thijsse(2011)]and successfully used to reproduce brittle or ductile fracture behaviors of Si NWs corresponding to different axial orientations and temperatures[Kang and Cai(2010);Liu and Shen(2012)],which were in agreement with experimental results[Zheng et al.(2009)].Besides,the potential is useful for determining elastic properties of Si NWs because of its reliable depiction of elastic constant,defect energies,cohesive energy,bulk modulus,surface energy,and vacancy formation energy,which are crucial for accurate calculation of elastic limits and incipient plastic responses of Si NWs under loading conditions[Liu and Shen(2012)].
All Si NWs models utilized in this work were cut from bulk single crystal silicon along a specific axial orientation. According to their axial orientations, three typical nanowires:<100>wires,<110>wires and<111>wires were constructed with different cross section shapes.Here,we first investigate the influence of aspect ratio by using rectangular cross section wires where the geometry effect is eminent.Then,the shape effect of cross section on the mechanical and fracture behaviors was studied in nanowires with different regular polygon cross sections,i.e.octagon,hexagon,and square.All wires had the same length of 543.1 Angstrom in the x direction,where lattice constant for silicon is 5.431 Angstrom.All wire surfaces,including lateral surfaces and end surfaces,are created as free surfaces.To consider the effect of the aspect ratio,we investigated a set of rectangular Si NWs.All wires considered are of the same length and nearly identical cross section area.Wire height h increases as wire width w decreases,forming different aspect ratios h:w at about 1:1,2:1,3:1 and 4:1 respectively.This length bias of two adjacent sides can cause the variation of mechanical properties.Besides,wires with different orientations are built to consider the axial orientation effect.The lattice orientations of each set of wires and cross section dimensions are listed in Table 1.

Table 1:Cross-section dimensions in terms of h:w for Si NWs with different lattice orientations,where w and h are defined in figure 1.All dimensions are in unit of nm.
By using the conjugate gradient method,silicon nanowires were statically relaxed to energy minimum positions with one end fixed and the other free.Initially,the atomistic configurations in Si NWs are not in equilibrium state for they have large proportional surfaces.To obtain an equilibrium state,surface atoms will reconstruct to reduce the surface stresses by introducing the residual stress into wire core,causing lateral and axial contraction in wires to get an equilibrated length.This initial stable length of each wire is recognized as L0.Temperature was kept at 10K during relaxation by using Nose-Hoover thermostat[Nose(1984);Hoover(1985)]for 20ps in canonical(NVT)ensemble and by rescaling atomic velocities for 20ps in micro-canonical(NVE)ensemble.The time step for the relaxation and the following loading process is 1fs.After initial relaxation,all wires are subjected to uniaxial tensile loading at the strain rate of 2×108/s.The tensile loading process was conducted by fixing one end of the wire,and applying velocities to atoms along the x direction that goes linearly from zero at the fixed end to a maximum value at the free end,creating a ramp velocity profile.This ramp velocity was used to avoid the emission of shock waves from the fixed end.
In this paper,all simulations are performed by using LAMMPS[Plimpton(1995);LAMMPS(2013)].The equations of motion are integrated by using velocity-Verlet algorithm.The axial stress and strain calculated here is global average for the entire system of atoms.The global stress represents uniaxial stress of the whole wire under tension,which is the average of the per-atom stress calculated using the virial theorem[Shen and Atluri(2004)],which takes the form α and

where N is the total number of atoms,is the distance between the two atoms,U is the potential energy,and V is the volume of the nanowire.The strain used in this work is the engineering strain which is defined aswhere L is the current wire length.The atomic structures in this work are visualized by Atomeye[Li(2003)].
3 Results and discussion
3.1 Cross section geometry effect
To investigate the cross-section geometry effect on the mechanical properties of silicon nanowires,we considered five sets of nanowires with different axial and surface orientations:[100]/[010][001](<100>a), [100]/[110][-110](<100>b),[110]/[001][-110](<110>a),[-110]/[110][001](<110>b),and[111]/[1-10][11-2](<111>).All wires have rectangular cross sections of the similar area but different aspect ratios ranging from 4:1,3:1,2:1,to 1:1 respectively,as listed in Table 1.Figure 2 and Figure 3 show the stress-strain responses of each case under uniaxial strain from zero to 30%.It was noted that stress of each case firstly increases linearly and then drops suddenly at a critical value,characterizing the onset of yielding.
Figure 2(a)shows the stress-strain curves of<100>a wires with varying aspect ratios.In the first deformation stage,tensile stresses of all wires increase almost linearly with increasing strain until the yielding points,where a typical crystalamorphous lattice transition initiates on the{100}side surfaces,as seen in Figure 5(a).In this case,by keeping cross section area constant at about 30 nm2,larger height corresponds with smaller width and hence larger aspect ratio(h:w).Among all cases,square wire,with the smallest height,has the largest yield stress.It is shown that yield stresses increase with decreasing aspect ratio.Here,we define the slop of stress-strain curve within the initial small strain regime as the effective Young’s modulus.As seen from Figure 4(c),the Young’s modulus of<100>a wire increases with decreasing aspect ratio.This increasing trend of yield stress in<100>a wire is also observed in Figure 4(b).It indicates that both yield stress and Young’s modulus are related to the cross section geometry in<100>a wires.The aspect ratio dependence of yield stress was also observed in<100>b rectangular wires,as shown in Figure 2(b).Similar to that of<100>a wires,<100>b wires have an increasing trend of yield stress with increasing aspect ratio.However,their stress-strain curves in the first deformation stage are overlapped,indicating that the effective Young’s Modulus is independent of the cross-sectional aspect ratio,as illustrated in Figure 4(c).

Figure 1:Atomic diagrams for rectangular(a),hexagonal(f),and octagonal(g)cross-section of<100>,<110>,and<111>SiNWs.The axial direction is along X.Surface normal to Y and Z directions are traction free.The lattice orientation along each direction is listed in Table 1.(b)-(e)present the different rectangular cross-sections with different aspect ratios,h:w,at 1:1,2:1,3:1,and 4:1,respectively.
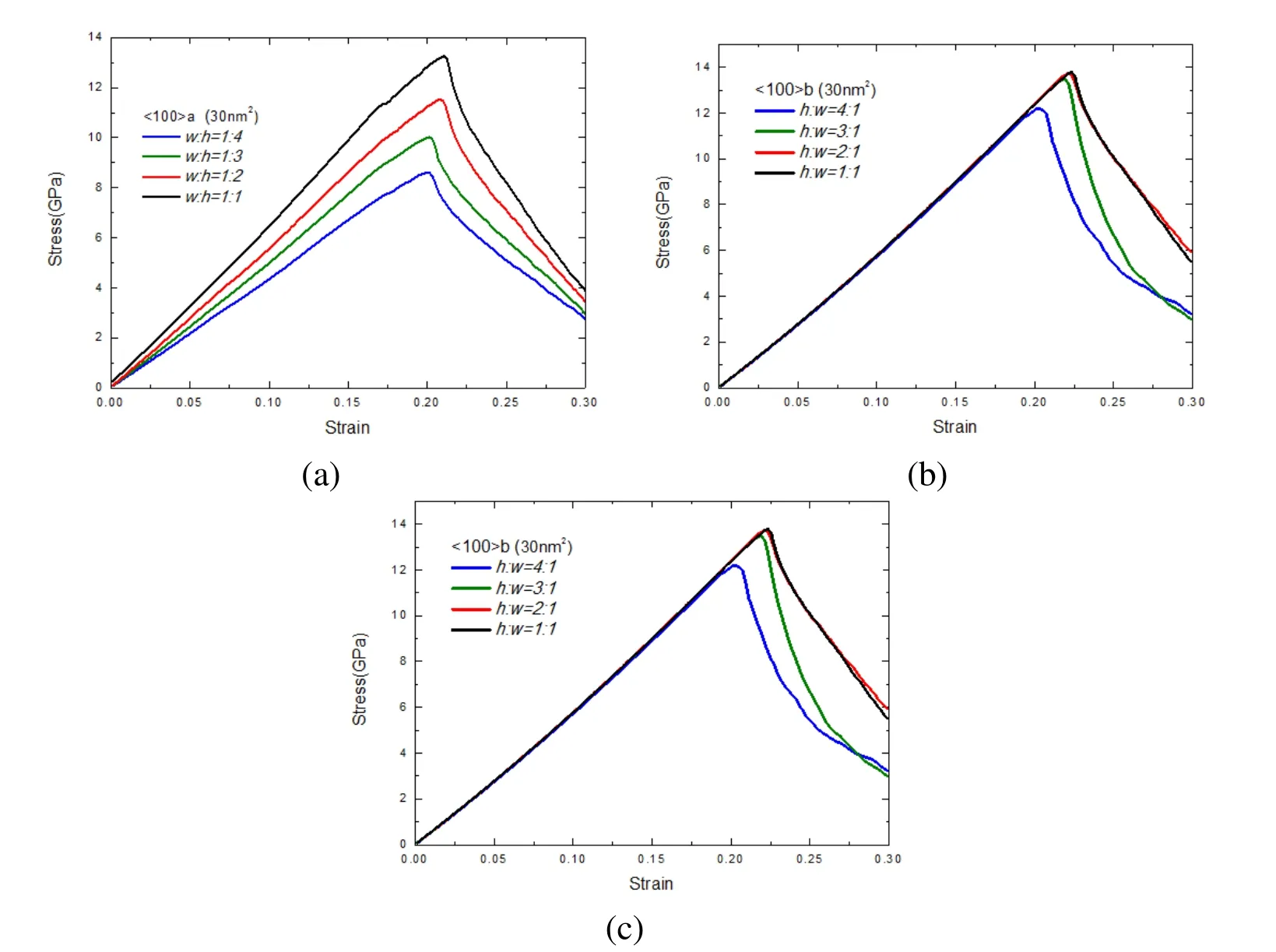
Figure 2:Stress-strain curves of<100>a(a)and<100>b(b)Si NWs with varying aspect ratios.
It was reported that the primary defect nucleation events of Si NWs vary distinctively according to their axial orientations[Liu and Shen(2012)].To study geometry effect on the yield stress,the influence of axial orientation on yield response should be considered.By using the same simulation technology,we modeled the tensile deformation of<110>a,<110>b and<111>wires.Their stress-strain curves are presented in Figure 3.For both<110>cases,yield stresses do not show a clear geometry dependence like that of two<100>cases.In<111>cases,stress-strain curves overlap in the initial deformation stage,indicating a constant elastic modulus.However,there is no linear correlation between elastic limits and their cross-section aspect ratios,as shown in Figure 3(c).
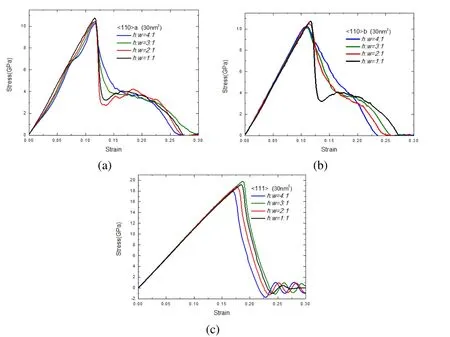
Figure 3:Stress-strain curves of(a)<110>a,(b)<110>b and(c)<111>Si NWs with varying aspect ratios.
Figure 4summarize the variations of yield strain,yieldstress,and Young’s modulus as a function of aspect ratios for Si NWs with different axial orientations.As shown in Figure 4(a),yield strains are almost constant regardless of aspect ratios for each axial orientation.The similar geometry independence can also be found for yield stress and Young’s Modulus.Except<100>a case,both yield stresses and Young’s Modulus for other kinds of wires fluctuate moderately,as can be seen in Figure 4(b)and(c).This geometry independence of Young’s Modulus is clearly confirmed by the variation of the normalized Young’s modulus(divided by the corresponding Young’s modulus of square wires),as presented in Figure 4(d).
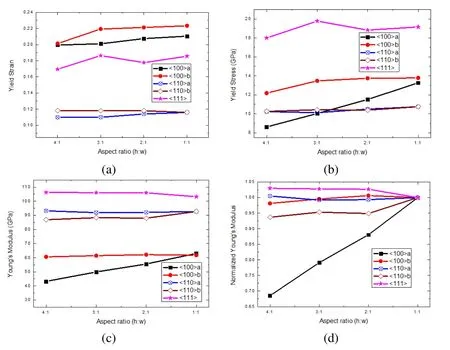
Figure 4:Yield stress,yield strain,Young’s modulus and normalized Young’s modulus as a function of aspect ratios for different sets of Si NWs.
From Figure 4,we note that the geometry dependence of<100>a wires is the most evident among all cases.To study this distinctive geometry dependence,we modeled a set of large<100>a wires by two-folding their transverse dimensions(with area of about 120 nm2).The stress-strain curves of large<100>a wires are shown in Figure 2(c).The curves are totally overlapped regardless of cross-section aspect ratios,even after the yielding.It illustrates that geometry effect of<100>a wires is negligible when the cross section length is larger than 10nm.With increasing transverse size,the surface-to-volume ratio decreases readily.Thus,the surface energy difference due to the change of cross section geometry can be neglected compared with the dominant bulk energy.

Figure 5:The incipient yield responses for different wires:(a)<100>a;(b)<100>b;(c)<110>b,and(d)<111>.Atoms in(a),(b),and(d)are colored by coordinate number with red,gray,green and burlywood for 5,4,3 and 2,respectively.Atoms in(c)are colored by the value of local shear strain(over 0.1)to highlight shear bands[Shimizu et al.(2007)].
Figure 5 presents the snapshots of incipient yielding responses for wires with different axial orientations. Typical inelastic yielding responses of<100>a,<100>b,<110>b and<111>wires are illustrated in Figure 5(a)-5(d),respectively.After the elastic limits,<110>b wires yield with partial dislocations nucleating from the lateral{110}surfaces,leaving multiple evident shear bands;<111>wires break with brittle cracking from lateral surfaces;while both<100>wires yield with crystal-to-amorphous(c-a)transition.These yielding responses do not change with varying aspect ratios.
Particularly,<100>a wires prefer to yield from the{100}surfaces(Figure 5(a));while<100>b wires tend to yield from the wire edges(Figure 5(b)).These preferential yielding sites are consistent with previous predictions by Zhu et al.[Zhu et al.
(2008)]and Isumi et al.[Izumi and Yip(2008)]based on activation energy theory.By correlating the nucleation sites with their local energetic states,we note that for<100>a wires,yielding events occur at high energetic{100}surfaces;while for<100>b wires,edges become more preferential than{110}surfaces to initiate c-a transition.
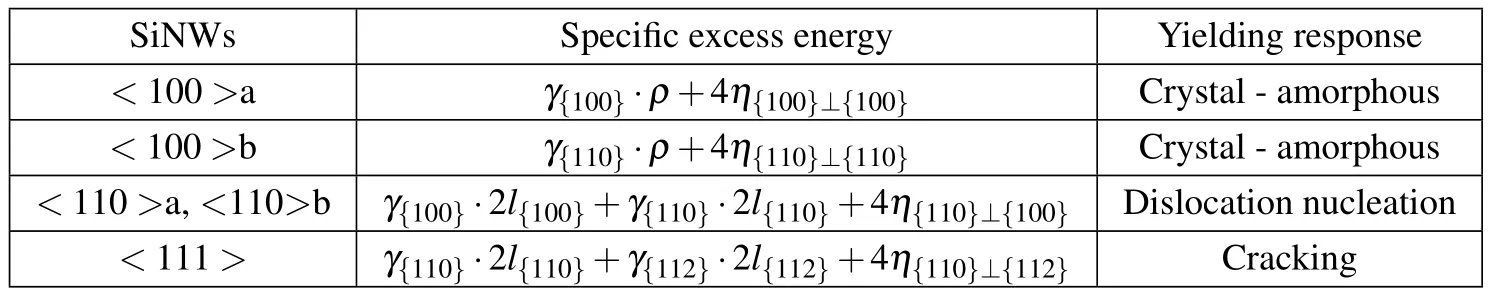
The geometry effect can also be explained to the excess energy based on equation(3).The excess energy per unit length for five sets of wires is listed in Table 2. From table 2,we notice that there are three factors that determine the specific excess energy of SiNWs.The first factor is the cross-section perimeter.With the same cross-section area,wires with larger aspect ratios will have longer perimeters and hence higher surface energy.Some researcher also reported that size dependent Young’s modulus was more likely to depend on cross-sectional perimeter than wire diameter[Justo et al.(2007)].The second factor is the specific surface energy.For example, unrelaxed surface energy of{100}facet is higher than that of{110}facet [Stekolnikov and Bechstedt(2005);Kang and Cai(2010)],thus<100>a wires have higher surface energy than<100>b wires.Furthermore,<100>a wires,with larger excess energy,show a more significant size dependence of Young’s modulus.The third factor is the specific edge energy.Although we simplified all the edges in this work as straight intersections of two dividing flat facets,there are still some ambiguities in the definition of edge energies[Hamilton(2006)],like edge length,facet area,and precise position of dividing facets.In this work,we only focus on the qualitative contribution of edge energies to the total excess energies,which will be further discussed in the next section.
For rectangular wires,edge energies do not change with varying aspect ratios.The variation of excess energy only results from the variation of surface energy,which has been proved to have limited influence on the elastic limits.First,the perimeter increment due to increasing aspect ratios is very small compared with the value of perimeter.Second,surface energy increases only when the longer sides of rectangular are of the higher energy facets.Therefore,for<100>wires,the variation of excess energy due to geometry effect is very limited and is only remarkable in small size.While for<110>and<111>wires,where the yielding events are determined by their axial orientation,the surface energy gap due to geometry effect is not sufficient to affect the elastic limits.
3.2 Cross section shape effect
Figure 6 shows the stress-strain responses of wires with three regular cross-section shapes:square,hexagon,and octagon.To consider the influence of axial orientation,we build five sets of cuboid boxes with different axial and surface orientations,as listed in Table 1.All wires considered here have the same length and transverse area.Figure 6 shows the stress-strain responses of each case for different regular shapes.Under the same loading,axial stress of each wire increases linearly until a critical yielding point,characterizing the initiation of inelastic event.For each axial orientation,yield stresses decrease in the same sequence:square wire has the largest yield stress;octagon wire has the moderate one;and hexagon wire has the smallest one.
Figure 7(a)shows yield stresses of wires with different axial orientations as a function of cross-section shape.For a certain axial orientation,yield stresses of each case show the same decreasing sequence with respect to their cross section shapes:square,octagon,and hexagon.The similar decreasing sequence is also observed for the Young’s Modulus of each case,as shown in Figure 7(b).Comparing the results of<100>a and<100>b wires with a specific shape,we note that yield stress and Young’s Modulus do not change significantly with varying lateral surfaces.Besides,previous results have suggested that geometry effect is not remarkable for<110>and<111>wires.Thus,we can conclude that surface effect is not a critical role for determining the shape dependence of elastic limits.
To understand the cross-section shape effect,we need to analyze the following influential factors:cross-sectional perimeter,specific surface energy,specific edge energy,and the individual contribution of either surface energy or edge energy.Among these factors,cross section perimeter and specific surface energy are primary constitutes of surface energies.For wires with different shapes,edge energy changes significantly with varying cross section shapes.However,the precise calculation of edge energy seems difficult due to the ambiguity in the definition of edge configuration and the quantitative calculation of edge energy.First,edge en-ergy is closely related to the precise definition of edge length and facet areas that are determined by the edge atomic configurations[Hamilton(2006)].Second,regular polygons with different number of sides have different inner angles.Third,edge atomic configuration and their adjacent facets may vary arbitrarily as lateral surfaces rotate around the axial orientation.

Figure 6:Stress-strain curves of(a)<100>a,(b)<100>b,(c)<110>a,(d)<110>b and(e)<111>Si NWs with varying shapes.

Figure 7:Yield stress and Young’s Modulus as a function of cross-section shape for different sets of Si NWs.
Nevertheless,by analyzing the mechanical behavior difference induced by geometry and shape effects,we can investigate the underlying mechanism based on fundamental energy theory.From energy view,the excess energy for rectangular wires with different aspect ratios is only determined by surface energy,while the excess energy for wires with different shapes is determined by both surface energy and edge energy.Edge energy is the only excess energy difference between the two effects.Considering the distinctive roles of the two effects,we can conclude that the edge energy is a crucial factor to determine the elasticity and subsequent yielding responses of SiNWs,which is consistent with our previous works[Liu et al.(2015)].Additionally,the decrease in yield stress of<100>a due to shape effect(4.1 GPa)is in the same level with the average gap due to axial orientation effect(i.e.yield stress gap between<100>and<111>wires is around 4.8 GPa).This indicates that shape dependence of elastic limits induced by edge effect can be considered as a comparable effect as that of axial orientation in SiNWs with diameter at a few nanometers.
4 Conclusions
In this work,atomistic simulations have been performed to investigate the geometry effect and shape effect on the elastic limits of silicon nanowires subjected to uniaxial tensile loading.For<100>wires with diameter less than 10 nm,the yield stress and the Young’s Modulus are remarkably dependent of their cross section aspect ratios.While for wires with<110>and<111>wires,no clear geometry dependence of elasticity is observed.It indicates that the geometry effect is easily affected by yielding responses determined by axial orientations.However,for wires with various regular cross sections,both yield stress and Young’s Modulus show the significant shape dependence regardless of their axial orientations.
老福点了一支烟,静静地坐下,突然想到应该去医院看看母亲了。他母亲是个虔诚的基督教徒,因为身体不好一直是医院的常客。久病成医,她经常给新来的病号当健康顾问。
Based on fundamental energy-based mechanics,we derive that the excess energy,including surface and edge energy,dominates the elasticity of silicon nanowires.For wires with the nearly small size,geometry effect arises from surface energy while shape effect originates from both surface energy and edge energy.Thus,the comparison between weak geometry effect and strong shape effect strongly suggests that the contribution of edge energy variation is crucial factor to determine the elastic limits of SiNWs.This could not only provide some insights into the effect of surface structure on the mechanical properties of silicon nanowires,but may be utilized in future engineering application as well.
Acknowledgement:The supports from NSFC(Grant No.11302161),China Postdoctoral Science Foundation(Grant No.2013M542339)and Open Research Fund of Key Laboratory of High Performance Complex Manufacturing,Central South University(Grant No.Kfkt2013-10)are appreciated.
Bandaru,P.;Pichanusakorn,P.(2010):An outline of the synthesis and properties of silicon nanowires.Semiconductor science and technology,vol.25,no.2,024003.
Cao,A.;Ma,E.(2008):Sample shape and temperature strongly influence the yield strength of metallic nanopillars.Acta Materialia,vol.56,no.17,pp.4816-4828.
Cui,Y.;Zhong,Z.;Wang,D.;Wang,W.U.;Lieber,C.M.(2003):High Performance Silicon Nanowire Field Effect Transistors.Nano Letters,vol.3,no.2,pp.149-152.
Diao,J.;Gall,K.;L.Dunn,M.(2004):Atomistic simulation of the structure and elastic properties of gold nanowires.Journal of the Mechanics and Physics of Solids,vol.52,no.9,pp.1935-1962.
Donadio,D.;Galli,G.(2010):Temperature Dependence of the Thermal Conductivity of Thin Silicon Nanowires.Nano Letters,vol.10,no.3,pp.847-851.
Hamilton,J.C.(2006):Edge energies:Atomistic calculations of a continuum quantity.Physical Review B,vol.73,no.12,125447.
Hoover,W.G.(1985):Canonical dynamics:equilibrium phase-space distributions.Physical Review A,vol.31,no.3,pp.1695-1697.
Huang,C.J.;Hung,T.Y.;Chiang,K.N.(2013).Estimation of the Mechanical Property of CNT Ropes Using Atomistic-Continuum Mechanics and the Equivalent Methods.CMC:Computers,Materials&Continua,vol.36,no.2,pp.99-133.
Izumi,S.;Yip,S.(2008):Dislocation nucleation from a sharp corner in silicon.Journal of Applied Physics,vol.104,no.3,033513.
Ji,C.;Park,H.S.(2006):Geometric effects on the inelastic deformation of metal nanowires.Applied physics letters,vol.89,no.18,181916.
Jin,S.;Fischetti,M.V.;Tang,T.-W.(2007):Modeling of electron mobility in gated silicon nanowires at room temperature:Surface roughness scattering,dielectric screening,and band nonparabolicity.Journal of Applied Physics,vol.102,no.8,083715.
Joseph,J.;Lu,Y.C.(2014):Finite Element Modeling of Compressive Deformation of Super-long Vertically Aligned Carbon Nanotubes.CMC:Computers,Materials&Continua,vol.42,no.1,pp.63-73.
Justo,J.;Menezes,R.;Assali,L.(2007):Stability and plasticity of silicon nanowires:The role of wire perimeter.Physical Review B,vol.75,no.4,045303.
Kang,K.;Cai,W.(2010):Size and temperature effects on the fracture mechanisms of silicon nanowires:Molecular dynamics simulations.International Journal of Plasticity,vol.26,no.9,pp.1387-1401.
LAMMPS.(2013):Available from:http://lammps.sandia.gov/.
Liang,H.;Upmanyu,M.;Huang,H.(2005):Size-dependent elasticity of nanowires:Nonlinear effects.Physical Review B,vol.71,no.24,241403.
Liu,Q.;Shen,S.(2012):On the large-strain plasticity of silicon nanowires:Effects of axial orientation and surface.International Journal of Plasticity,vol.38,no.0,pp.146-158.
Liu,Q.;Wang,L.;Shen,S.(2015):Effect of surface roughness on elastic limit of silicon nanowires.Computational Materials Science,vol.101,pp.267-274.
Lucas,M.;Mai,W.;Yang,R.;Wang,Z.L.;Riedo,E.(2007):Aspect ratio dependence of the elastic properties of ZnO nanobelts.Nano letters,vol.7,no.5,pp.1314-1317.
Mclaren,A.;Valdes-Solis,T.;Li,G.;Tsang,S.C.(2009):Shape and size effects of ZnO nanocrystals on photocatalytic activity.Journal of the American Chemical Society,vol.131,no.35,pp.12540-12541.
Nose,S.(1984):A unified formulation of the constant temperature molecular dynamics methods.The Journal of Chemical Physics,vol.81,no.1,pp.511-519.
Plimpton,S.(1995):Fast parallel algorithms for short-range molecular dynamics.Journal of Computational Physics,vol.117,no.1,pp.1-19.
Qian,X.;Liu,H.;Guo,Y.;Song,Y.;Li,Y.(2008):Effect of aspect ratio on field emission properties of ZnO nanorod arrays.Nanoscale research letters,vol.3,no.8,pp.303-307.
Qu,F.;Santos,D.;Dantas,N.;Monte,A.;Morais,P.(2004):Effects of nanocrystal shape on the physical properties of colloidal ZnO quantum dots.Physica E:Low-dimensional Systems and Nanostructures,vol.23,no.3,pp.410-415.
Shen,S.;Atluri,S.(2004):Atomic-level stress calculation and continuum-molecular system equivalence.Computer Modeling in Engineering and Sciences,vol.6,pp.91-104.
Shi,W.-S.;Peng,H.Y.;Zheng,Y.F.;Wang,N.;Shang,N.G.;Pan,Z.W.;Lee,C.S.;Lee,S.T.(2000):Synthesis of large areas of highly oriented,very long silicon nanowires.Advanced Materials,vol.12,no.18,pp.1343-1345.
Shimizu,F.;Ogata,S.;Li,J.(2007):Theory of shear banding in metallic glasses and molecular dynamics calculations.Materials transactions,vol.48,no.11,pp.2923-2927.
Shir,D.;Liu,B.Z.;Mohammad,A.M.;Lew,K.K.;Mohney,S.E.(2006):Oxidation of silicon nanowires.Journal of Vacuum Science&Technology B,vol.24,no.3,pp.1333-1336.
Shuttleworth,R.(1950):The surface tension of solids,Proceedings of the Physical Society.Section A,vol.63,no.5,pp.444.
Sivakov,V.A.;Voigt,F.;Berger,A.;Bauer,G.;Christiansen,S.H.(2010):Roughness of silicon nanowire sidewalls and room temperature photoluminescence.Physical Review B,vol.82,no.12,125446.
Sohn,Y.-S.;Park,J.;Yoon,G.;Song,J.;Jee,S.-W.;Lee,J.-H.;Na,S.;Kwon,T.;Eom,K.(2010):Mechanical properties of silicon nanowires.Nanoscale research letters,vol.5,no.1,pp.211-216.
Stekolnikov,A.;Bechstedt,F.(2005):Shape of free and constrained group-IV crystallites:Influence of surface energies.Physical Review B,vol.72,no.12,125326.
Timonova,M.;Thijsse,B.J.(2011):Optimizing the MEAM potential for silicon.Modelling and Simulation in Materials Science and Engineering,vol.19,no.1,015003.
Yang,Z.;Lu,Z.;Zhao,Y.-P.(2009):Shape effects on the yield stress and deformation of silicon nanowires:A molecular dynamics simulation.Journal of Applied Physics,vol.106,no.2,023537.
Zhang,T.-Y.;Luo,M.;Chan,W.K.(2008):Size-dependent surface stress,surface stiffness,and Young’s modulus of hexagonal prism[111] β-SiC nanowires.Journal of Applied Physics,vol.103,no.10,104308.
Zheng,K.;Han,X.;Wang,L.;Zhang,Y.;Yue,Y.;Qin,Y.;Zhang,X.;Zhang,Z.(2009):Atomic Mechanisms Governing the Elastic Limit and the Incipient Plasticity of Bending Si Nanowires.Nano Letters,vol.9,no.6,pp.2471-2476.
Zhu,T.;Li,J.;Samanta,A.;Leach,A.;Gall,K.(2008):Temperature and Strain-Rate Dependence of Surface Dislocation Nucleation.Physical Review Letters,vol.100,no.2,025502.
1State Key Laboratory for Strength and Vibration of Mechanical Structures,School of Aerospace,Xi’an Jiaotong University,Xi’an 710049,PR China.
2E-mail:qunfengliu@mail.xjtu.edu.cn

