同侧双滚子从动件盘形凸轮轮廓的解析设计法
胡昌志,崔建昆,王 枫
(上海理工大学机械工程学院,上海 200093)
同侧双滚子从动件盘形凸轮轮廓的解析设计法
胡昌志,崔建昆,王枫
(上海理工大学机械工程学院,上海 200093)
摘要:文中采用同侧双滚子从动件结构设计了新型形锁合盘形凸轮机构;采用解析算法之包络原理生成了双滚子从动件盘形凸轮的内外轮廓,并通过算例具体介绍了凸轮轮廓包络原理生成法的计算机实现过程。
关键词:包络;双滚子;凸轮;轮廓
0 引 言
凸轮传动结构简单、紧凑,能通过设计凸轮轮廓以实现从动件预期的运动规律[1-2]。张玉华等用相对运动法设计盘形凸轮轮廓并开发了计算机辅助设计程序[3]。Paulo Flores用Matlab对盘形凸轮机构尺寸进行了优化设计[4]。常勇等对共轭、槽道和等径等形锁合盘形凸轮机构的尺寸综合问题作深入、系统的研究[5]。
本文设计了采用同侧双滚子从动件的新型形锁合盘形凸轮机构,用同侧双滚子夹住凸轮的凸边,如此在凸轮运转中既可以减少单滚子从动件的槽道磨损和减弱振动,还可以避免力锁合凸轮机构的失效情形。但本设计需要为双滚子从动件盘形凸轮机构设计两条匹配的轮廓。使用解析法之包络原理可以较方便地生成两条匹配精确的轮廓,较之几何法,精度更高,不容易出错。最后,在算例里介绍如何用基本的常用软件完成同侧双滚子从动件盘形凸轮轮廓的设计。
1 求解包络公式
根据包络的定义,某个曲线簇的包络线是跟该曲线簇的每条线都有至少一个相切点的一条曲线。那么任意两条相邻曲线的隐函数为
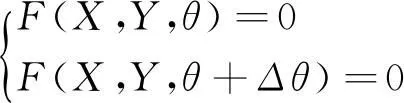
(1)
其相切点坐标的隐方程为
(2)
当Δθ趋近无穷小。
联立曲线簇和相切点的隐方程
(3)
就可求出每个相切点的坐标,得出包络线的隐方程。
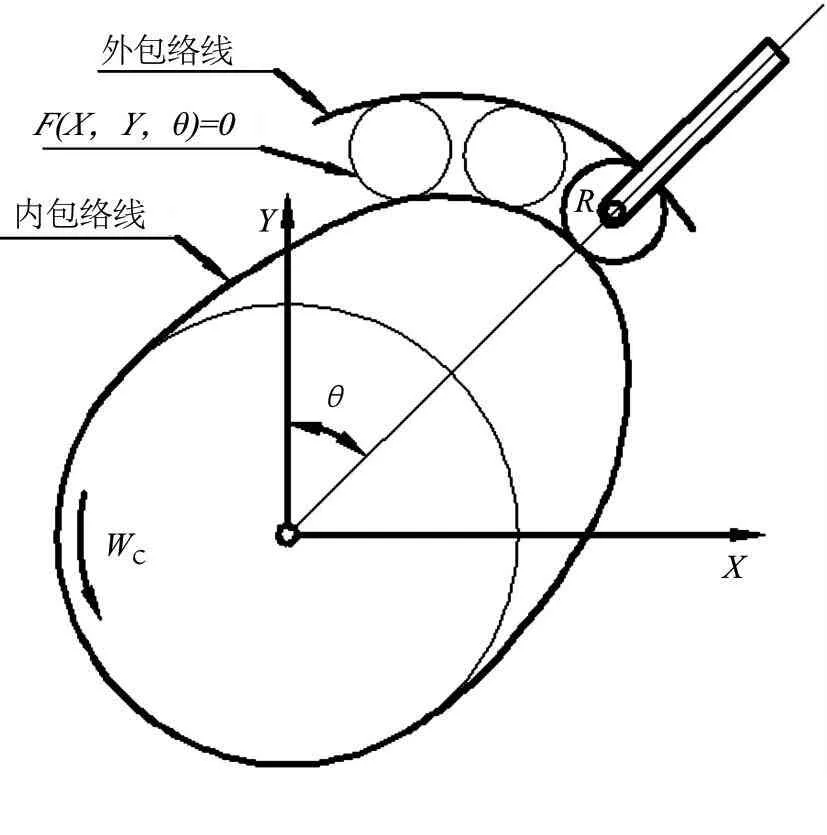
图1 单滚子包络示意图
如图1,滚子R在凸轮上滚过一圈,滚子所经过的区域由一簇圆组成,圆簇的边界就是内外两条包络线。圆簇的隐方程为F(X,Y,θ)=0,其包络线的隐方程就是以下面两个方程消去参数θ得到,
(4)
式中,X、Y为圆簇上各个圆的坐标;θ为圆簇的参数,不同的θ对应圆簇上不同的圆。
2 凸轮轮廓的生成
如图2,外滚子R1形成的圆簇方程是:
(5)
式中,(XR1,YR1)是滚子R1的圆心坐标,Rr是滚子R1、R2的半径;θ为凸轮转过的角度。
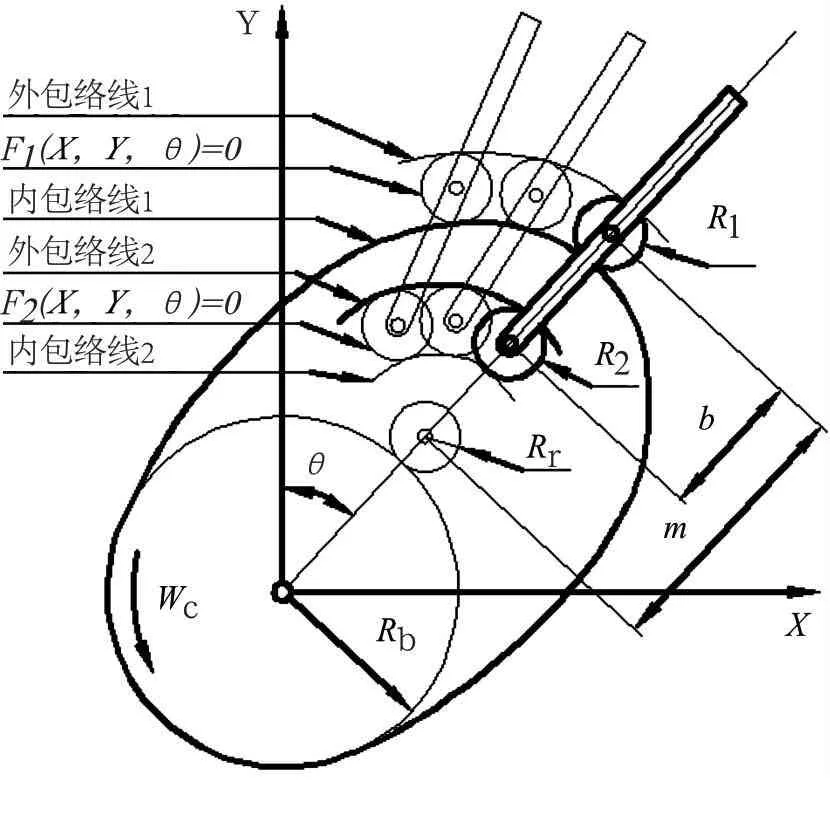
图2 同侧双滚子从动件凸轮轮廓的生成
式(5)对θ求偏微分有:
(6)
其中滚子R1的圆心坐标由几何关系得到:
式中,Rb是凸轮的基园半径;m是滚子在各个转角的径向位移。
而圆心坐标对θ的求导为
(7)
把式(6)、(7)分别代入式(5),联立成方程组,可解出两条包络线方程:
(8)
上式中先取正号再取负号得到的是内包络线,先取负号再取正号得到的是外包络线。结合实际的需要,做相应的取舍,这里外滚子只要内包络线用于生成凸轮外轮廓。
对于同侧的内滚子R2,其与外滚子R1类似,区别在圆心坐标上:
(9)
式中,Rb是凸轮的基园半径;m是滚子在各个转角的径向位移;b是同侧双滚子的中心距。式(9)的圆心坐标对θ求导有
(10)
套用计算外滚子包络线的公式可得内滚子的两条包络线方程:
(11)
先取正号再取负号得到的是内包络线,先取负号再取正号得到的是外包络线。结合实际做相应的取舍,这里内滚子只要外包络线用于生成凸轮内轮廓。
3 算 例
参考文献查手册或[1-2],选用一种常用的运动规律,这里用修正正弦运动规律来举例。所设计的双滚子从动件盘形凸轮的基本参数为基圆半径Rb=100 mm,滚子半径Rr=10 mm,双滚子中心距b=30 mm。
上升、下降段修正正弦运动规律曲线方程分别为:
(12)
式中,m是滚子在各个转角的径向位移;L为凸轮机构推程;β为推、回程运动角占一个周期的比例;θ为凸轮转过的角度。
式(12)对θ求导有:
(13)
3.1 计算凸轮轮廓离散点坐标
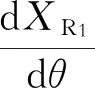
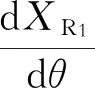
3.2 画CAD图
在AutoCAD命令行里输入样条曲线命令“spline”,然后把离散点的合并后的坐标一次性粘贴到后续提示命令行里,便可得到离散点驱动样条线生成的同侧双滚子从动件凸轮轮廓线,如图4。
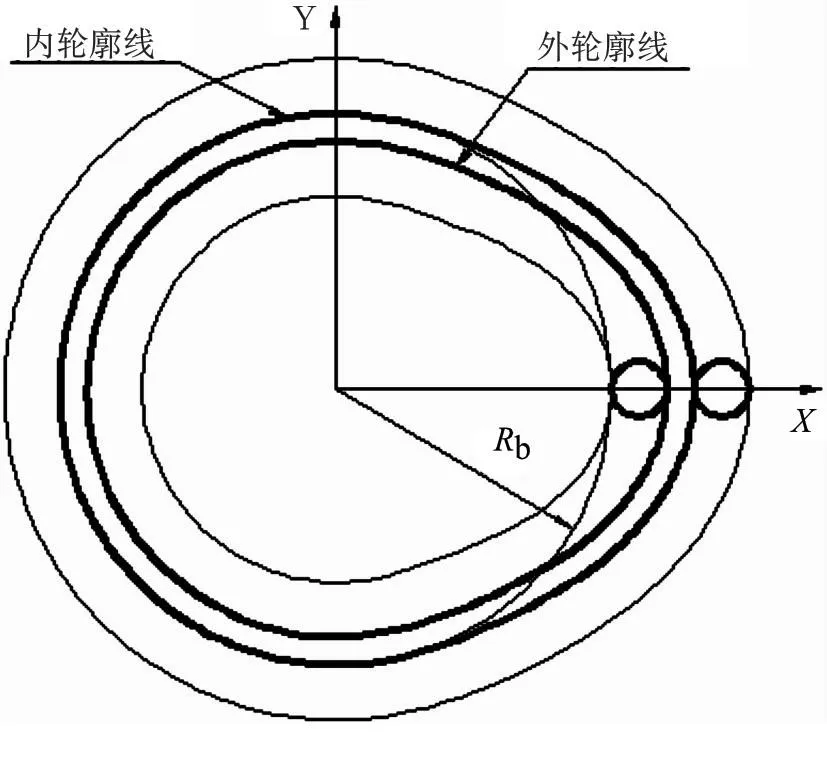
图4 凸轮轮廓线图
4 结 论
数值解法求解同侧双滚子盘形凸轮轮廓具有精度高,适合程序实现的优点,能保证后续机加工的精度。同侧双滚子从动件尽管在凸轮轮廓径向长度变化很大的地方会减少凸轮凸边的宽度,只要选择较大的双滚子圆心距就能克服这个缺陷。同侧双滚子从动件还是可以减少单滚子从动件的槽道磨损和减弱振动,还可以避免力锁合凸轮机构的失效情形。包络原理求解同侧双滚子从动件凸轮机构在计算机上用Excel的计算能力和AutoCAD的绘图能力就可实现。文中给出的具体计算步骤和操作方法可以为广大的生产一线工作者提供切实可行的凸轮轮廓设计方案,具有一定的新颖性和较高的实用性。至于同侧双滚子从动件盘形凸轮机构凸轮凸边厚度的变化规律以及回程中压力角的变化还有待研究。
[1]陈秀宁.机械设计基础[M]. 杭州:浙江大学出版社,2007.
[2]Shigley J E.Theory of Machines and Mechanisms[M].New York:McGraw Hill,1995.
[3]张玉华,辛重镐. 设计平面凸轮轮廓的新方法[J]. 机械工程学报,2004,40(1):33-37.
[4]Paulo Flores. A Computational Approach for Cam Size Optimization of Disc Cam-Follower Mechanisms With Translating Roller Followers[J].ASME J. Mech. 2013.
[5]常勇,杨富富.作平面运动滚子从动件形锁合凸轮机构的第Ⅱ类机构综合问题[J].机械工程学报,2012,48(1):39-46.
崔建昆(1964-),男,四川成都人,博士,副教授,研究方向:机械传动和机械设计及理论。
设计应用
An Analytical Approach to Obtaining Planar Cam Profile with Single Side Double Roller-Follower
HU Chang-zhi, CUI Jian-kun, WANG Feng
(College of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)
Abstract:A novel positive-drive planar cam mechanism with single side double roller-follower is designed in this article and its profile is generated using the envelop principle. An example is documented to show how to handle this task with computer.
Key words:envelop principle; double roller-follower; cam; profile
中图分类号:TH112
文献标识码:A
文章编号:1009-3664(2015)02-0063-03
作者简介:胡昌志(1989-),男,湖北黄石人,机械电子专业硕士研究生在读, 研究方向为机械传动。
收稿日期:2014-12-18

