基于有限元极限平衡法的生基坪滑坡稳定性分析

刘汉东，李冬冬，王忠福

(华北水利水电大学 资源与环境学院，河南 郑州 450045)

刚体极限平衡法和有限元法是边坡稳定性分析的主要方法．刚体极限平衡法将岩土体视为刚体，未考虑岩土体变形对边坡稳定性的影响，并且在计算安全系数时进行了诸多假设，其计算结果的准确性值得商榷．但该方法给出了明确的安全系数用于评价边坡的稳定性，在工程中得到了广泛的应用．有限元法通过计算边坡内部任一点的应力状态，可以考虑岩土体变形对其稳定性的影响，但未能给出明确的安全系数，不便于工程应用．

因此，将刚体极限平衡法［1］与有限元法［2］结合起来对边坡进行稳定性分析逐渐成为新的趋势，将有限元计算出的应力场应用到极限平衡法中求解安全系数，既能考虑岩土体变形对边坡稳定性的影响，又可以给出工程中广泛应用的安全系数． 许多学者对此进行了相关的研究与探索． Brown 和King［3］首次将有限元极限平衡法应用到线弹性土质边坡的稳定性分析中．Liu 等［4］应用极限平衡法、有限元极限平衡法、强度折减法对几个简化的滑坡进行分析，得到相应的安全系数及临界滑面，发现各种方法之间存在高度的一致性．曾亚武等［5］通过一个简化边坡介绍了应用有限元极限平衡法分析边坡稳定性的过程．王连捷等［6］研究了存在已知滑动面和不存在滑动面时有限元极限平衡法计算滑坡安全系数的方法．徐卫亚等［7］在边坡稳定性分析中引入了图论中解决最短路问题的Dijkstra 算法，建立了基于Dijkstra 算法的有限元极限平衡方法． 李红军等［8］将有限元极限平衡法应用到三维边坡中，得到的稳定分析结果与刚体极限平衡法和有限元强度折减法的结果保持一致，认为将该法应用于空间边坡稳定性安全评价是可行的．多数研究者仅将有限元极限平衡法应用于简单的理想模型，少有将其应用到实际边坡工程中．笔者将该方法应用到重庆生基坪滑坡的稳定性分析中，并将计算结果与极限平衡法、有限元强度折减法的结果进行对比分析．

1 边坡稳定性分析方法

1．1 有限元极限平衡法

通过有限元法计算得出岩土体的应力场分布，在滑动面已知的情况下，便可求出滑面各点的法向应力σ 与剪应力τ;应用极限平衡法计算滑面各点的安全系数．

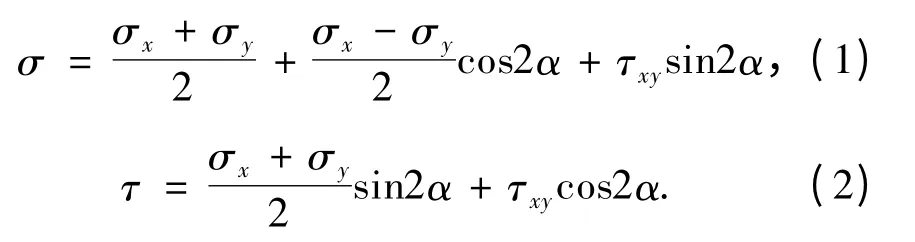
式中:σx、σy为滑面上一点的正应力，τxy为剪应力;α 为滑面的法线与X 轴的夹角．

根据摩尔－ 库伦强度准则及极限平衡法计算安全系数的原理便可得到有限元极限平衡法计算安全系数的公式，即:

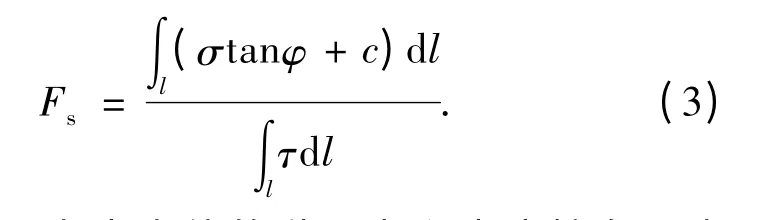
式中:c、φ 分别为岩土体的黏聚力和内摩擦角;l 为滑面长度．

1．2 有限元强度折减法

Zienkiewicz 等［9］最早将强度折减的思想引入到边坡稳定性分析中，近年来许多学者和研究人员针对应用强度折减法分析边坡的稳定性进行了深入的研究，并将其与有限元法进行了对比［10－12］． 强度折减法［13］中边坡稳定的安全系数定义为:使边坡刚好达到临界破坏状态时，对岩土体的抗剪强度进行折减的程度．即定义安全系数为岩土体的实际抗剪强度与临界破坏时的折减后的抗剪强度的比值．

强度折减法:

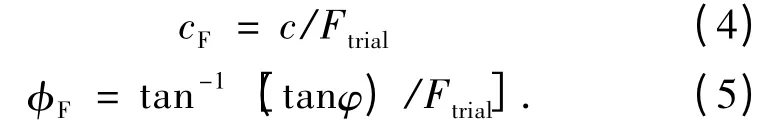
式中:cF、F 分别为折减后的黏聚力和内摩擦角;Ftrial为折减系数．

通过调整岩土体的强度指标c、φ 值，对边坡稳定性进行数值分析，不断地增加折减系数，反复计算，直至边坡达到临界破坏状态，此时得到的折减系数即为安全系数Fs．

1．3 屈服准则

有限元计算中，屈服准则的选择将对计算得到的安全系数产生显著影响．摩尔－ 库伦屈服准则是当前岩土工程中广泛应用的屈服准则，笔者在有限元计算时即选用此准则．其表达式为:

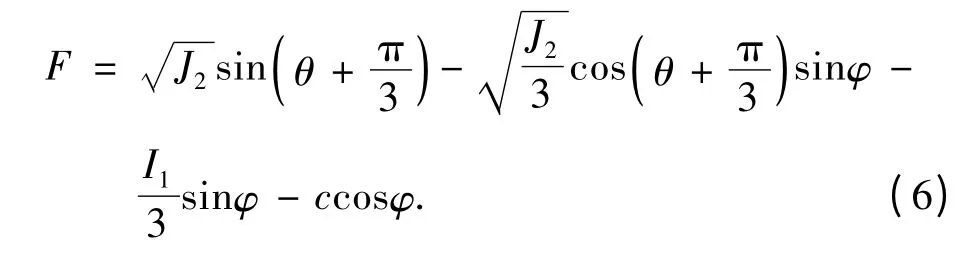
其中:I1= σx+ σy+ σz，

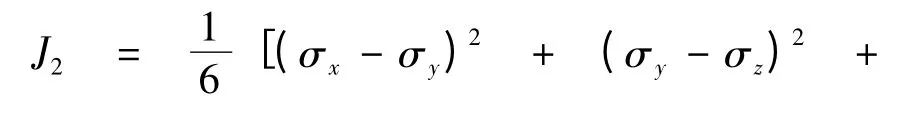
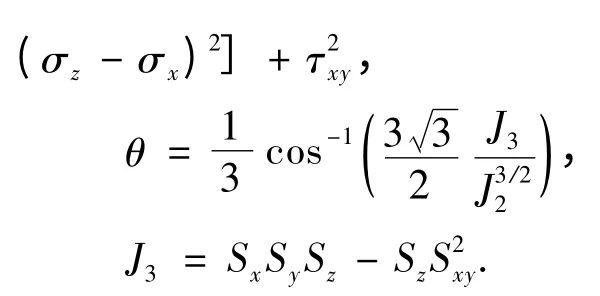
式中:I1为第一应力不变量;J2为第二应力偏量不变量;θ 为Lode 角;J3为第三应力偏量不变量;S 为偏应力张量;c 为材料黏聚力;φ 为材料的内摩擦角．

在有限元计算中，需要计算F/J2和F/J3的值，而当θ = 0°及θ = 60°时，屈服面出现角点，此时F/J2和F/J3均为无限大，因此需作如下处理［5］:

当θ = 0° 及θ = 60° 时代入式(6)中可得

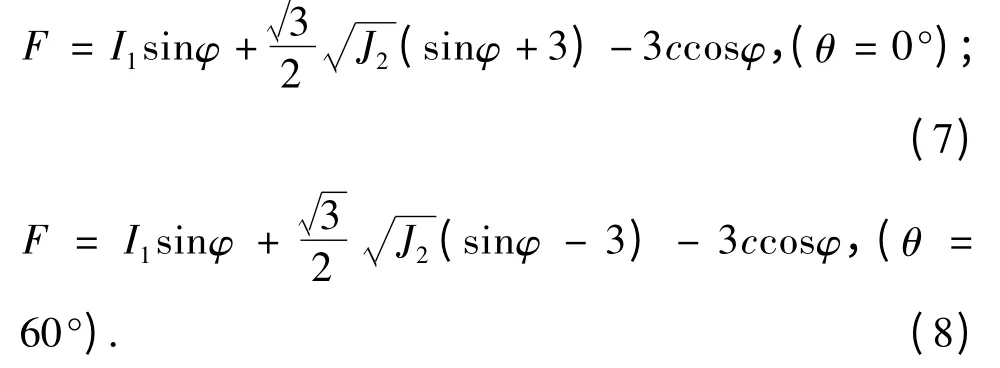
由式(7)和式(8)得

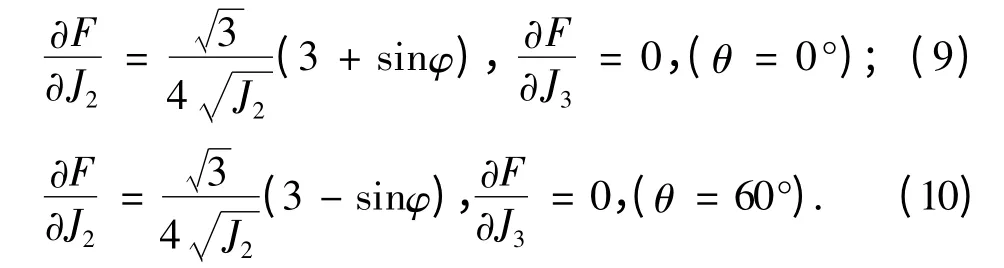
当θ ≠0° 及θ ≠60° 时，由式(6)计算F/J2和F/J3．

2 生基坪滑坡体稳定性分析

应用上述有限元极限平衡法对生基坪滑坡进行稳定性分析，并将计算所得的安全系数与刚体极限平衡法、强度折减法所得的进行对比分析．

2．1 工程概况及模型建立

重庆市彭水县保家镇生基坪滑坡为一古滑坡．滑坡平面形态总体上略呈舌形，宽度约200 m，纵向长约600 m，面积约1．2 ×105m2，滑体平均厚度约17 m，体积约2．04 ×105m3，为一推移式大型中层土质滑坡，主滑方向为128°．滑坡平面图如图1 所示．

该滑坡体中2—2 剖面(图1)为主剖面，将其作为计算剖面，容重采用滑体现场大重度试验及室内试验测试结果，滑带土抗剪强度值通过室内试验值、野外判定、反演计算3 种方法综合确定．计算参数取值见表1．

将计算剖面2—2 简化为二维平面的应变问题．计算模型长度取1 500 m，坡脚向前延伸250 m，坡体向下延伸70 m．计算模型共划分548 个节点，496个单元．模型左右两端水平方向固定，底部水平方向和竖直方向均固定．模型网格如图2 所示．

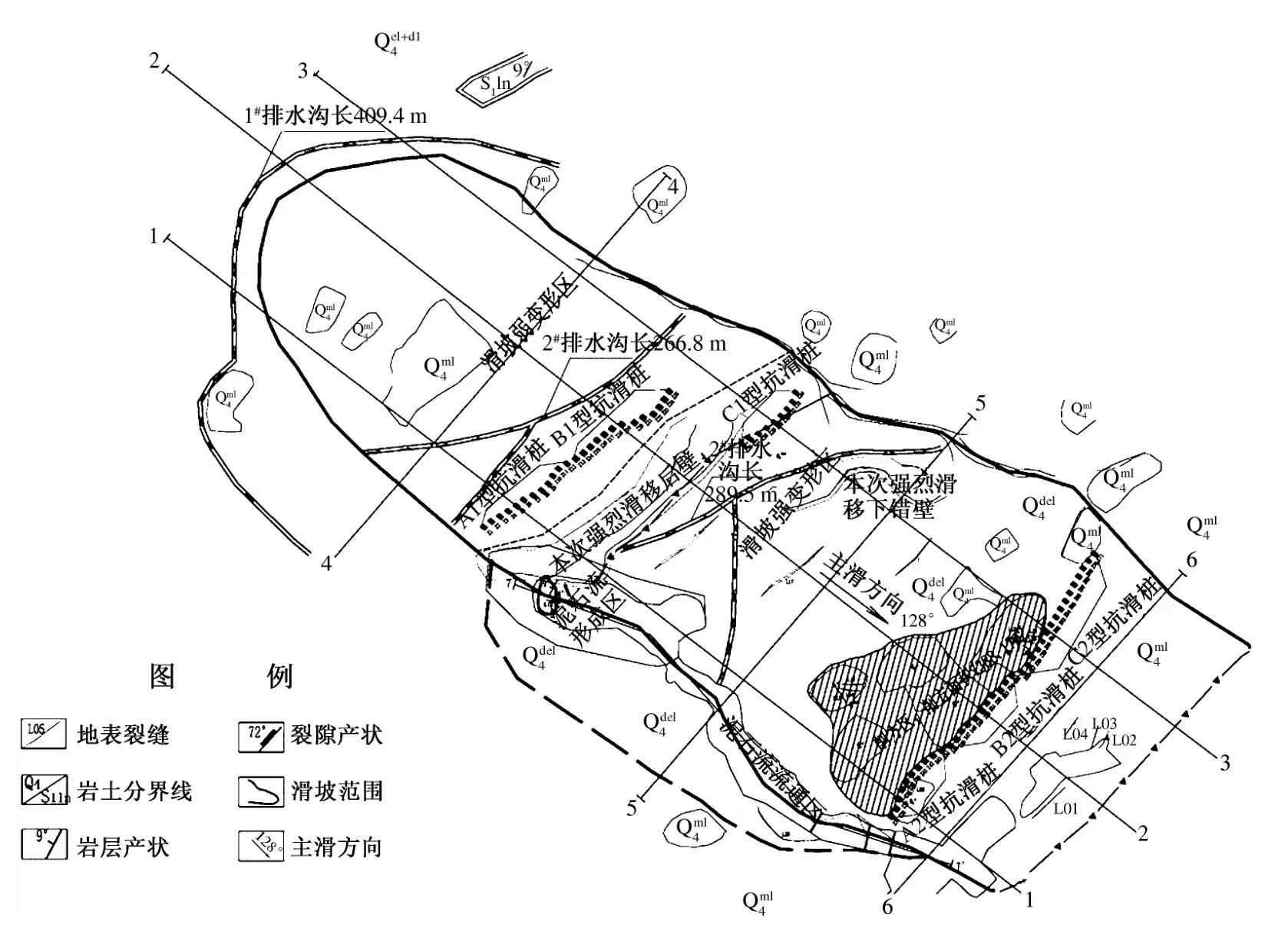
图1 生基坪滑坡平面示意图

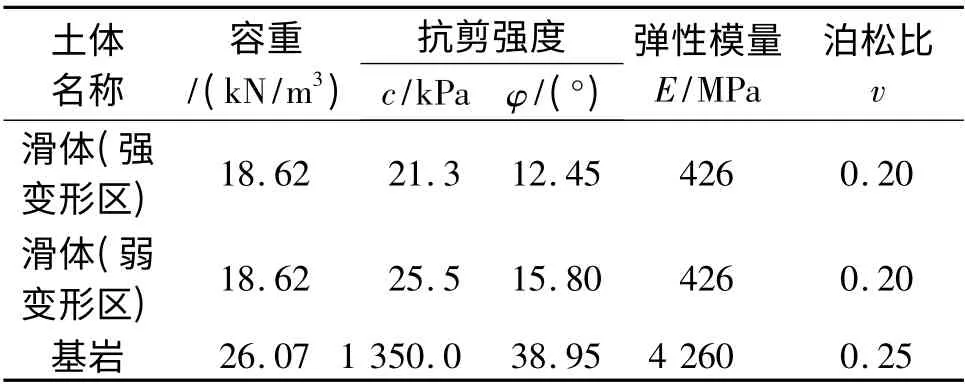
表1 2—2 剖面岩土特性参数

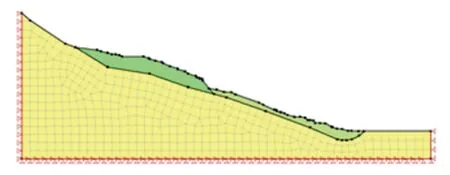
图2 有限元计算模型

2．2 有限元计算结果

经有限元计算，得到坡体最大正应力等值线图和最大剪应力等值线图，分别如图3 和图4 所示，图5 为沿滑动面各点的正应力与剪应力分布情况．

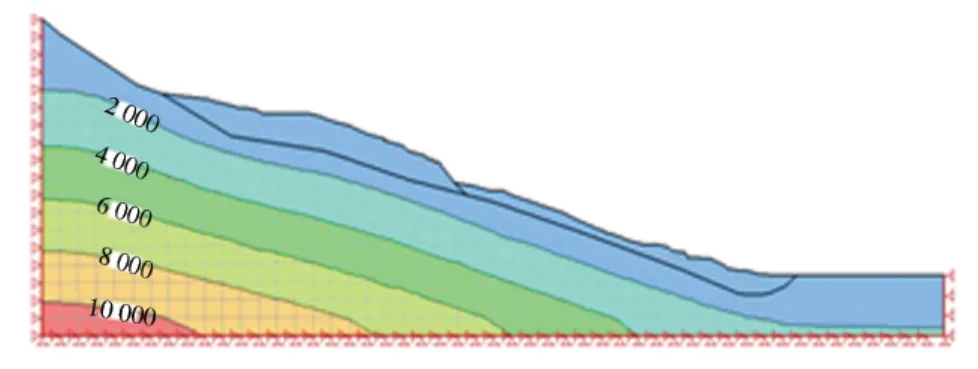
图3 最大正应力等值线图(单位:kPa)

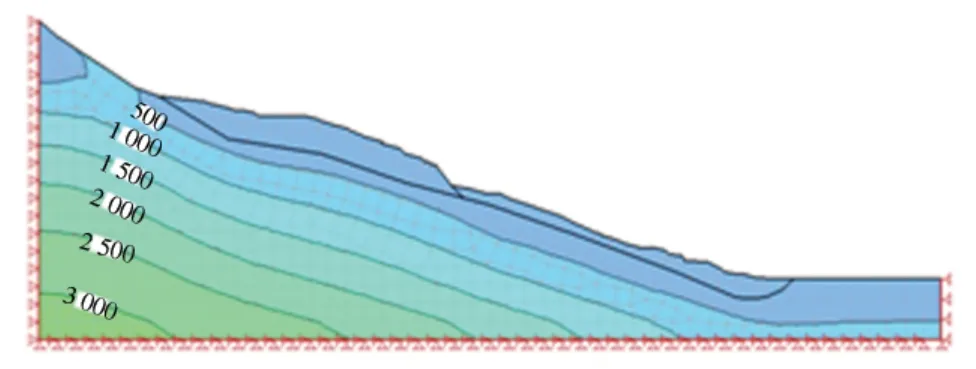
图4 最大剪应力等值线图(单位:kPa)

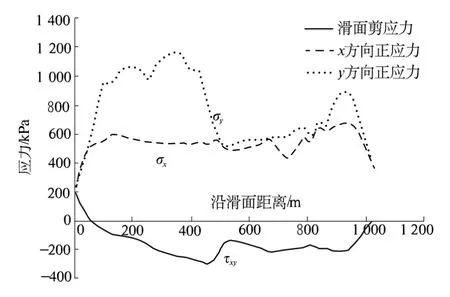
图5 沿滑动面各点的正应力与剪应力分布

2．3 边坡稳定性安全系数

根据式(1)和式(2)，分别求得沿滑面各点垂直于滑面的法向应力和平行于滑面的剪应力，如图6所示．

根据图6 给出的法向应力和剪应力，由式(3)求得滑坡总体安全系数为1．064． 图7 为沿滑动面各点的安全系数，由此可以确定沿滑动面岩土体强度的发挥程度．由图7 可知，滑坡后缘和前缘岩土体强度的发挥程度比较低，而滑坡体中部强度发挥程度比较高．根据岩土体强度发挥程度的不同可相应采取不同的防护措施．

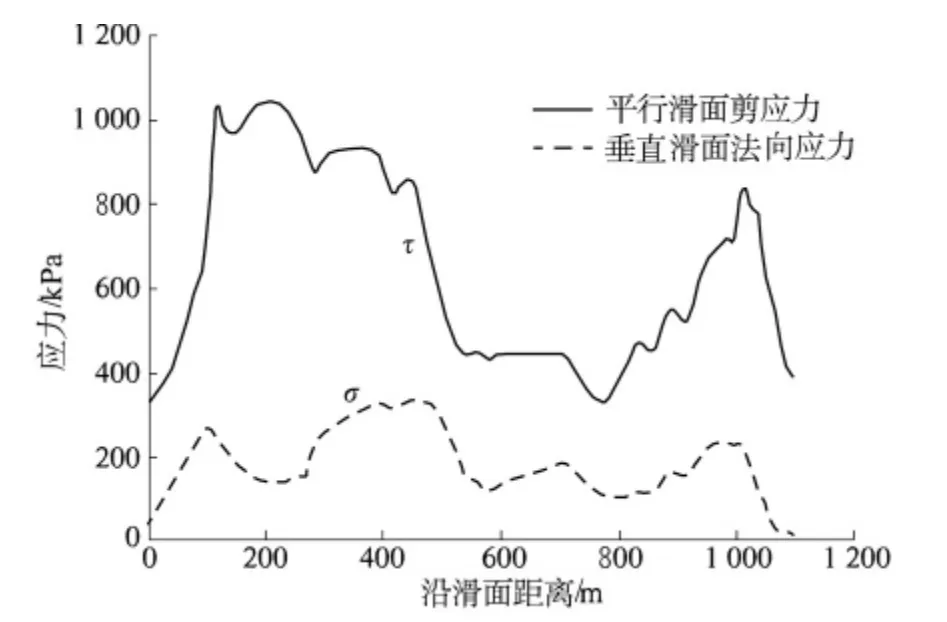
图6 滑动面各点的法向应力和剪应力

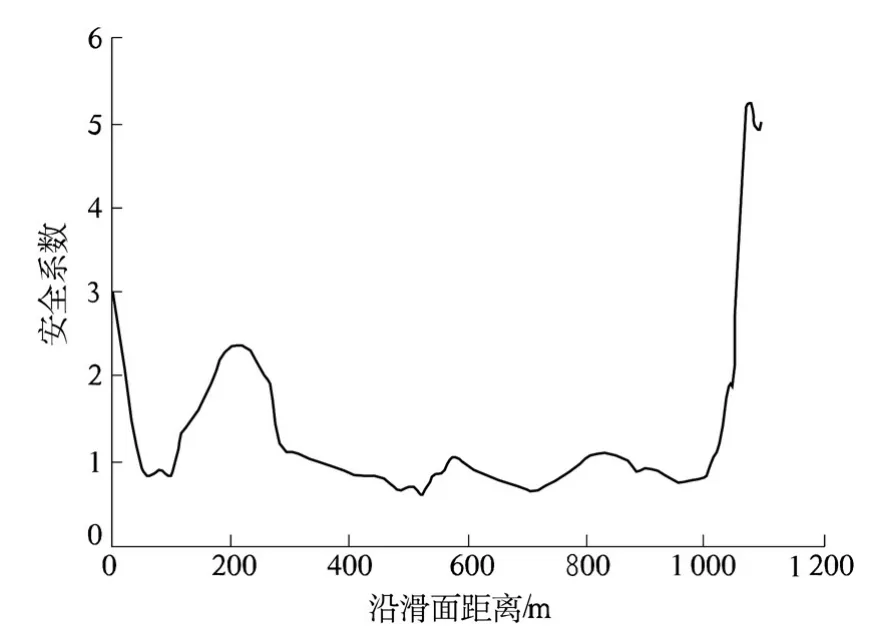
图7 沿滑动面各点安全系数

2．4 与其他计算方法对比分析

表2 为不同计算方法所得的安全系数计算结果及其与有限元极限平衡法计算结果的相对差值．

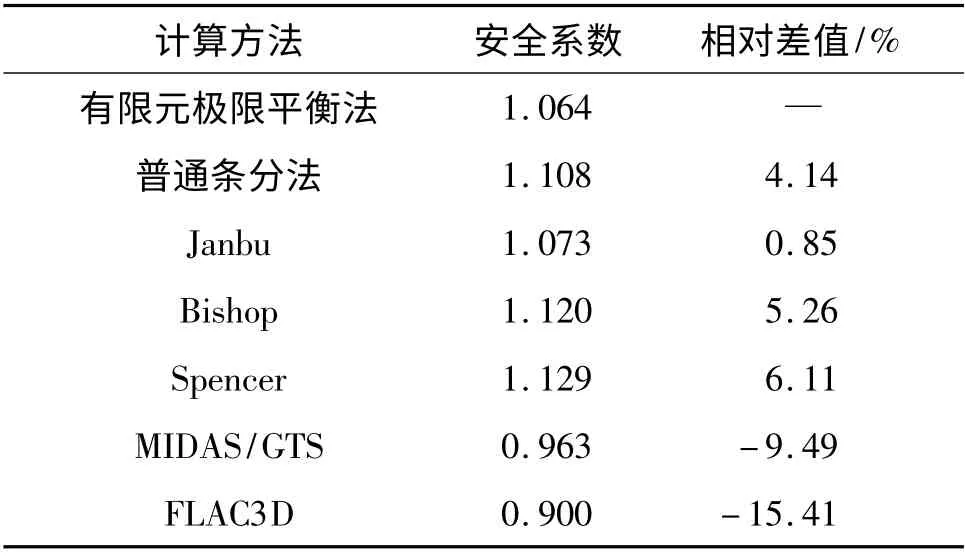
表2 不同计算方法所得的安全系数

由表2 可知:普通条分法与有限元极限平衡法计算的安全系数相对差值为4．14%;Janbu 法与有限元极限平衡法的相对差值最小，为0．85%;Bishop法的为5．26%;Spencer 法的为6． 11%;通过FLAC3D 有限差分强度折减法计算所得的安全系数与有限元极限平衡法的相对差值最大，为－15．41%;通过MIDAS/GTS 有限元强度折减法计算所得的安全系数与有限元极限平衡法的计算结果的相对差值为－9．49%．

由其他计算方法所得的安全系数与有限元极限平衡法计算所得的安全系数相比可以看出，本文所采用的4 种刚体极限平衡法的计算结果与有限元极限平衡法的相差较小，在7%以内，而强度折减法的计算结果与有限元极限平衡法的计算值相差较大，均大于9%．

3 结 语

1)将有限元计算所得坡体应力场应用于极限平衡法求解边坡安全系数，一方面考虑岩土体变形对边坡稳定性的影响，另一方面又能给出工程中常用的评价滑坡体安全性的安全系数．

2)将有限元极限平衡法应用到生基坪滑坡体的稳定性计算中，并将其计算结果与传统极限平衡法、强度折减法进行对比分析，发现:有限元极限平衡法所得的安全系数比4 种刚体极限平衡法的均大，与Janbu 法的相对差值最小，为0．85%，与Spencer 法的相对差值最大，为6．11%;与强度折减法相比，有限元极限平衡法计算的安全系数较大，即所计算出的安全系数介于刚体极限平衡法与强度折减法之间．

3)有限元极限平衡法不仅能给出边坡总体安全系数，还可以确定沿滑动面各点岩土体强度的发挥程度，据此可采取不同的优化防护措施对边坡进行加固处理．

［1］陈祖煜．土质边坡稳定分析原理·方法·程序［M］．北京:中国水利水电出版社，2003．

［2］赵尚毅，时卫民，郑颖人． 边坡稳定性分析的有限元法［J］．地下空间，2001，21(增刊1):450 －454．

［3］Brown C B，King I P． Automatic embankment analysis:Equilibrium and instability conditions［J］． Geotechnique［Internet］，1966，16:209 －219．

［4］Liu S Y，Shao L T，Li H J．Slope stability analysis using the limit equilibrium method and two finite element methods［J］．Computers and Geotechnics，2015，63:291 －298．

［5］曾亚武，田伟明．边坡稳定性分析的有限元法与极限平衡法的结合［J］． 岩石力学与工程学报，2005，24(增刊2):5355 －5359．

［6］王连捷，周春景，吴珍汉，等．用有限元极限平衡法分析边坡的稳定性［J］．中国地质，2008，35(5):1031－1036．

［7］徐卫亚，周家文，邓俊晔，等． 基于Dijkstra 算法的边坡极限平衡有限元分析［J］．岩土工程学报，2007，29(8):1159 －1172．

［8］李红军，邵龙潭．有限元极限平衡法在三维边坡中的应用研究［J］．铁道工程学报，2011，152(5):17 －21．

［9］Zienkiewicz O C，Humpheson C，Lewis R W． Associated and non-associated visco-plasticity and plasticity in soil mechanics［J］．Geotechnique［Internet］，1975，25:671－689．

［10］刘汉东．水电工程岩质高边坡安全度标准研究［J］．华北水利水电学院学报，1998，19(1):41 －45．

［11］Griffiths D，Lane P． Slope stability analysis by finite elements［J］．Geotechnique，1999，49(3):387 －403．

［12］Zheng H，Liu D F，Li C G．Slope stability analysis based on elasto-plastic finite element method［J］． International Journal for Numerical Methods in Engineering，2005，64(14):1871 －1888．

［13］郑颖人，赵尚毅．有限元强度折减法在土坡与岩坡中的应用［J］． 岩石力学与工程学报，2004，23(19):3381 －3388．